迟滞非线性系统辨识与补偿控制研究*

阳 丹，王湘江

(南华大学机械工程学院，湖南衡阳421001)

0 引 言

磁致伸缩材料、压电陶瓷等智能材料均存在迟滞非线性现象。非线性特性的存在使智能材料重复性降低，瞬态位置响应速度变慢，可控性变差。为减小这种非线性特性所造成的不良影响，更好地发挥智能材料的性能，很多科研机构和研究人员正在从事迟滞非线性系统建模及控制方法等方面的相关研究，因此，许多迟滞建模方法和控制技术应运而生，并日趋成熟、完善［1］。在迟滞建模方面，Preisach模型是应用最广的一类迟滞模型［2-4］，1935年 Preisach等人建立了比较完善的迟滞模型—Preisach模型。1997年PingGe为了适应迟滞补偿的需要，建立了改进的Preisach模型。并用该模型大幅提高了迟滞系统的跟踪精度。压电陶瓷等智能材料的迟滞系统可以通过串联Preisach模型和系统传递函数准确反映其迟滞特性。在非线性迟滞模型辨识方面［5］，可以通过最小二乘法进行离线辨识，最小二乘思想最早于1975年由高斯(K.F.Gauss)提出来，被广泛应用于系统辨识和参数估计，甚至在许多辨识方法失效的情况下，最小二乘法却可以提供对问题的有效解决办法［6］。也可以依据对象的输入/输出数据，不断地辨识模型参数以进行在线辨识，随着科学研究的不断进行，通过在线辩识，模型会变得越来越准确，越来越接近于实际，神经网络［7-8］是20世纪末迅速发展起来的一门高等技术。已经在各个领域得到了广泛地应用，神经网络辨识为解决未知不确定非线性系统的辨识问题提供了一条新的思路。神经网络辨识方法可以精确地模拟出迟滞系统。在辨识模型不断的改进下，基于辨识模型综合出来的控制方法也将随之不断的改进。

本研究通过辨识的传递函数建立其逆模型控制系统，根据对迟滞逆模型是否进行在线调整，可将控制方案分为动态控制和静态控制方案。本研究属于静态控制。静态补偿方案以 Ping Ge，Samir Mittal，Sumiko Majima等为代表［9］。笔者在逆模型控制过程中加入PID控制器［10］，通过调节PID参数，使控制系统逐渐适应误差变化，最终将迟滞系统调整到一个满意的工作状态。本研究针对智能材料迟滞非线性现象，进行迟滞系统建模;然后，对迟滞系统进行系统辨识;最后，对辨识系统进行控制研究。

1 迟滞系统的建立

通过研究得出将Preisach模型和系统传递函数串联得到的迟滞系统能够达到比较理想的迟滞效果，迟滞系统能够准确地反应压电陶瓷等智能材料的迟滞特性。在相关的研究中已经得到论证［11］。迟滞系统结构如图1所示。

图1 迟滞系统结构

本研究采用Preisach模型做为纯迟滞模型，具有普遍意义。Preisach模型由最简单的滞回发生器γαβ叠加构造而成。尽管每个发生器仅能表现出一个局部记忆滞回，但叠加在一起就表现为全局记忆性。给定这一族发生器任意的权重函数μ(α，β)(该函数具体数值的选用取决于Preisach函数的构造)。其函数式为:

式中:x(t)—驱动器的输出，u(t)—输入。

由式(1)可知，Preisach模型函数为连续的双重积分函数，所以不便于模拟仿真，于是把积分模型离散处理，将Preisach模型采用 Matlab/Simulink中的43个backlash算子叠加形成。通过设置backlash中deadband width参数达到叠加效果。每个算子的deadband width为1/7，这样得到的Preisach模型迟滞特性能够满足研究需求。输入信号通过多个迟滞算子叠加在一起得到迟滞输出信号。本研究采用u(t)=sin(πt)作为输入信号，得到的迟滞模型如图2所示。

图2 控制信号的迟滞模型

然后本研究将得到的Preisach模型和系统传递函数串联起来，二阶传递函数作为系统传递函数在压电陶瓷等智能材料具有一般代表性，如超磁致伸缩微位移驱动器(GMA)中，根据GMA机电系统动力学模型和牛顿第二定律可知GMA系统传递函数为二阶传递函数［12］，在Matlab中通过模型转化命令可以实现离散传递函数和连续传递函数之间的相互转换［13］。所以本研究采用离散二阶传递函数作为系统传递函数具有一般代表性，选用传递函数为G(z)=(-0.2z+0.2)/(z2-1.1z+0.1)，输入信号通过迟滞系统得到输出y(t)如图3所示。

2 迟滞模型的系统辨识

图3 通过迟滞模型的输出信号

通过输入信号u(t)和迟滞系统得到输出数据y(t)进行模型的参数辨识。根据辨识方法和精度不一样，系统参数辨识可以分为离线辨识和在线辨识。离线辨识常用的辨识方法为最小二乘法。在线辨识方法比较广泛，本研究主要采用神经网络辨识方法。

本研究通过分析最小二乘法和神经网络辨识原理，然后对迟滞系统进行辨识，再比较离线辨识和在线辨识的辨识结果。

2.1 最小二乘法辨识

离散系统函数表达式为:

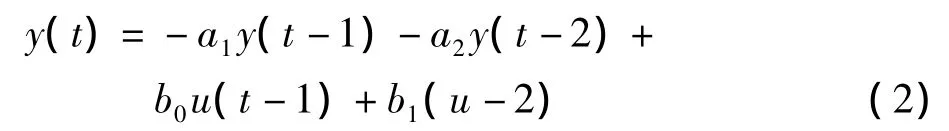
本研究采用最小二乘法来确定模型参数，待估参数向量θ为:

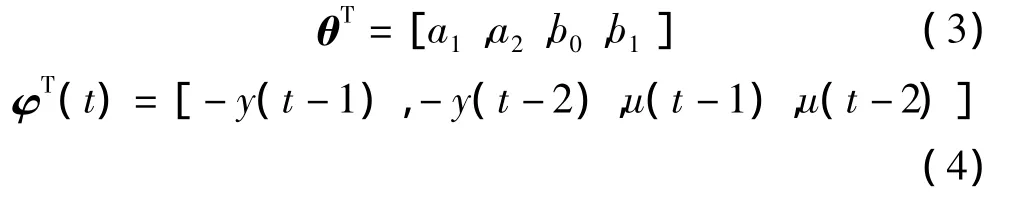
式中:φ—数据向量。

对象式(2)可以写成如下最小二乘形式:

利用最小二乘法得到系统辨识参数θ为:

通过迟滞系统输入信号u(t)和输出数据y(t)得到最小二乘法辨识参数为:

式(2)在零初始条件下，取Z变换:

得到的辨识传递函数为:

辨识原理图如图4所示。实际输出和最小二乘法辨识输出以及比较误差如图5所示，输入信号y(t)和辨识系统输出信号yG(t)之间误差e(t)是比较小的，从而确认式(7)二阶模型的有效性。

图4 辨识原理示意图

图5 实际输出和最小二乘法辨识输出以及比较误差

2.2 神经网络辨识

由于神经网络优越的自调整和自适应性，本研究采用神经网络辨识方法进行迟滞模型参数辨识，神经网络的辨识方法如图6所示。

图6 神经网络辨识方法示意图

神经网络辨识原理为:

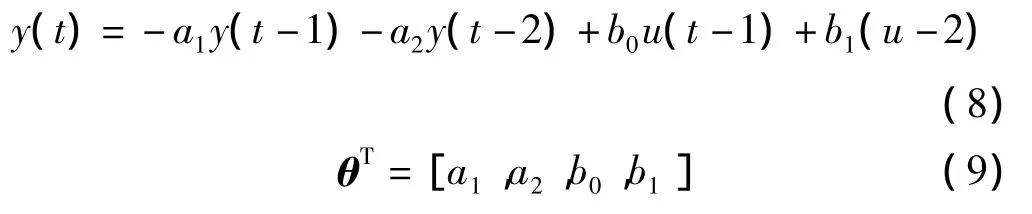
令θ为神经网络权值w:

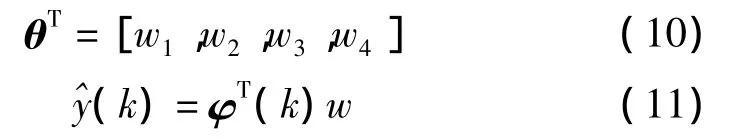
神经网络训练规则为:

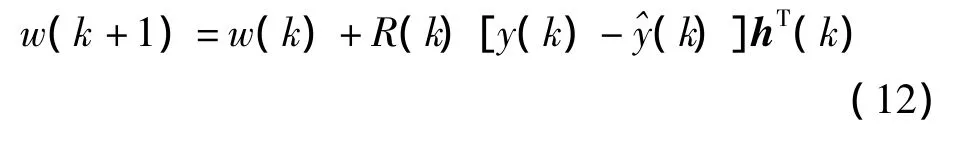
其中:

式中:ci—加权因子，0 ＜ci＜1，ci=μi，0 ＜ μ ＜1。

图7 神经网络辨识模型参数

本研究使用离线辨识二阶模型估计参数作为神经网络在线辨识加权系数的初始值。这将减少在线辨识的计算时间。根据式(11)和式(12)，得到迟滞系统的神经网络辨识模型。二阶模型辨识参数结果如图7所示。神经网络辨识模型输出和迟滞模型实际输出以及相关的误差如图8所示。因为误差很小，辨识输出和实际输出几乎重叠。

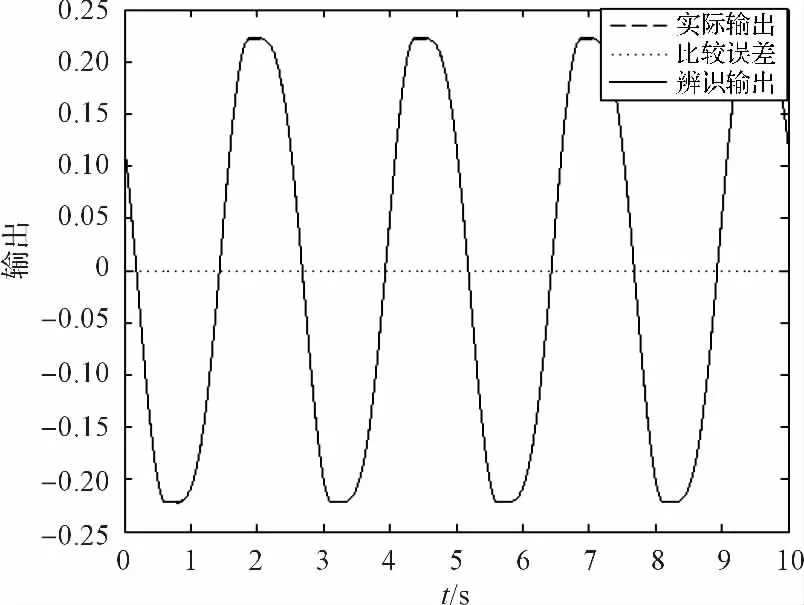
图8 实际输出和神经网络输出以及比较误差

根据图8得到迟滞系统输出和神经网络辨识输出误差已经非常小，可以得出Matlab/Simulink搭建的神经网络辨识模型能够准确地辨识出迟滞系统的模型参数，从而说明神经网络辨识方法的有效性。

通过观察比较离线和在线辨识，离线最小二乘法每次的辨识结果只能得到一组参数，这样的辨识程序运行速度快，但是得到的参数误差相对比较大。神经网络辨识采用在线辨识，对参数进行实时调整，程序运行速度比离散有所减慢，但使得辨识参数和传递函数系数之间误差最小化，能找到最优辨识参数。

3 控制系统的设计和执行

通过系统辨识得到辨识传递函数模型，本研究针对辨识传递函数模型提供了两种控制方法:一种是逆模型控制系统，这是一种完全的开环控制系统，不需要任何反馈数据的控制器;另一种是前馈逆模型PID控制系统，这是一种闭环反馈系统，能够实时调整参数达到最佳控制效果。

3.1 建立逆模型控制系统

逆模型控制系统原理如图9所示。

图9 逆模型控制器示意图

如果传递函数不稳定，那么式(7)不能直接用作建立逆模型控制系统，需要构建逆模型G-1(z)，逆模型有点滞后于迟滞系统，通过之前设计好的函数模型G1(z)和最优函数模型G2(z)来设计逆模型。即:

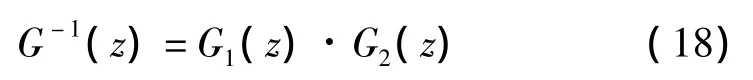
其中，之前设计好的函数模型为:

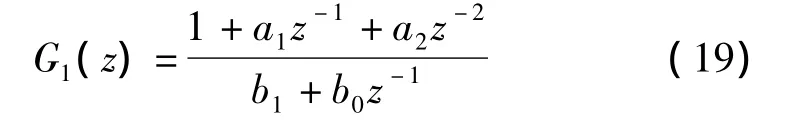
最后，得到输出y(k)为:

逆模型稳定的前提是辨识得到传递函数必须稳定，根据离散传递函数稳定条件，传递函数必须是最小相位系统，其零点必须在z平面的单位圆里。如果传递函数是稳定的，那么直接用传递函数倒数可以得到系统的逆模型。即:

最优函数模型为:

其中:Δ≥1。

最优函数模型是不稳定的，因为它的极点不在z平面单位圆里面，所以G2(z)可以扩展为:

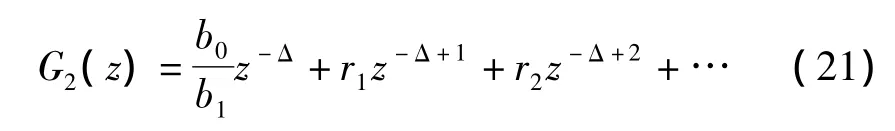
由于辨识传递函数是稳定的，直接通过式(17)可以得到逆模型。通过逆模型控制得到补偿效果如图10所示。

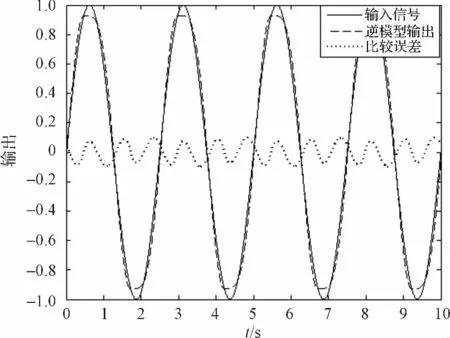
图10 输入信号和逆模型控制输出以及比较误差

3.2 建立前馈逆模型PID控制

为了提高系统的鲁棒性，更好操作参数变化。本研究设计一种前馈逆模型PID控制方法。其原理如图11所示。

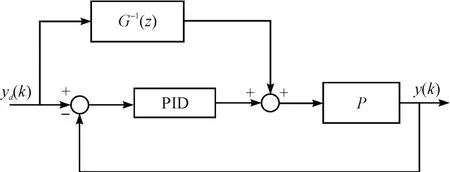
图11 前馈逆模型PID控制器示意图

前馈逆模型PID控制数学模型为:

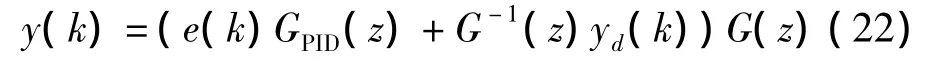
其中:

前馈逆模型PID控制器的控制结果如图12所示，通过图12得出:输入信号与前馈逆模型PID控制的输出信号已经很接近，两者之间误差已经很小。为了更好说明前馈逆模型PID控制器的有效性，测试前馈PID控制器的控制能力，可以在不同频率下进行控制。本研究还采用u(t)=2sin(2πt)+10sin(0.5πt)作为输入信号，得到控制结果如图13所示。图12、图13结果说明控制器可以有效跟踪动态输入信号，实现对迟滞系统有效补偿控制。

图12 输入信号为u(t)=sin(πt)控制结果

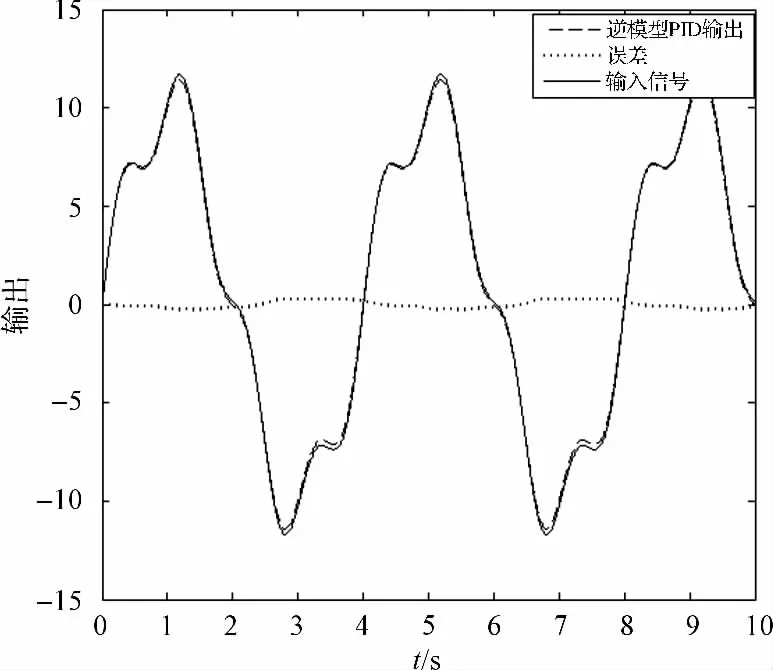
图13 输入信号为u(t)=2sin(2πt)+10sin(0.5πt)控制结果

通过相同输入信号u(t)=sin(πt)作用，逆模型控制方法和前馈逆模型PID控制方法的补偿结果如图10、图12所示。为了更直观地比较两种控制方法的控制效果，本研究采用均方根误差来比较。其计算公式为:

得到的比较结果如表1所示。最后可以得到前馈逆模型PID控制方法能更有效进行迟滞补偿。

表1 两种控制方法的RMS误差

4 结束语

本研究运用Preisach模型和系统传递函数建立了迟滞系统，通过辨识结果说明离线和在线辨识方法都能有效辨识迟滞系统，从辨识误差分析结果可以看出，神经网络在线辨识方法能非常精确地辨识迟滞系统。由迟滞系统补偿结果来看，迟滞非线性已基本得到消除。该结果说明所提出的前馈逆模型PID控制是可行的，但此时要注意PID参数的选取，避免出现饱和、振荡等情况的发生。

本研究采用的辨识方法和控制技术能够有效地降低智能材料中迟滞现象的影响。其辨识和控制方法具有普遍意义，可以推广到其他系统中的迟滞非线性补偿控制中。

［1］唐志峰，吕福在，项占琴.超磁致伸缩微位移驱动器的非线性迟滞建模及控制方法［J］.机械工程学报，2007，43(6):55-61

［2］龚大成，唐志峰，吕福在，等.非线性Preisach理论与超磁致伸缩执行器高阶迟滞建模［J］.机械工程学报，2009，45(12):252-256.

［3］VISINTIN A.On hysteresis in elasto-plasticity and in ferromagnetism［J］.International Journal of Non-linear Mechanics，2007，37(8):1283-1298.

［4］李 黎，刘向东，侯朝桢，等.混合Preisach迟滞模型及其性质研究［J］.光学精密工程，2008，16(2):279-284.

［5］YEH T J，LU S W，WU T Y.Modeling and identification of hysteresis in piezoelectric actuators［J］.Journal of Dynamic Systems，Measurement and Control，2006，128(2):189-196.

［6］MÜHLICH M，MESTER R.The Role of Total Least Squares in Motion Analysis［C］//Proceedings of 5th European conference on Computer Vision，ECCV'98.Germany:Springer Verlag，1998:305-321.

［7］LI X，FU X.Synchronization of chaotic delayed neural networks with impulsive and stochastic perturbations［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16(2):885-894.

［8］闻 新，周 露，李 翔，等.Matlab神经网络仿真与应用［M］.北京:科学出版社，2003.

［9］陈 辉，邵 林.基于MATLAB的数字PID控制器仿真［J］.连云港职业技术学院学报，2004，19(2):31-32.

［10］齐剑玲，曾玉红，刘慧芳.PID调节器的仿真研究［J］.海淀走读大学学报，2004，8(1):69-71.

［11］魏燕定，陶惠峰.压电驱动器迟滞特性的Preisach模型研究［J］.压电与声光，2004，26(5):364-367.

［12］陈定方，舒 亮，卢全国，等.超磁致伸缩致动器建模与控制仿真［J］.机械工程学报，2007，43(8):12-16.

［13］魏克新，王云亮.MATLAB语言与自动控制系统设计［M］.北京:机械工业出版社，2004.