基于TMS320F2812的永磁直线电机伺服控制研究*

张 勇，姚艺华，卢琴芬

(浙江大学电气工程学院，浙江杭州310027)

0 引 言

随着机械加工行业的不断发展，在直线驱动方面也提出了更高的要求，传统的旋转电机加上“齿轮+滚珠丝杠”的传动方式逐渐被效率更高的直线直驱技术所代替。由于永磁直线伺服电机具有的高精度、快速响应、零传动等优点，已成为直线直驱技术中的应用热点。永磁直线伺服电机通常采用电流、速度、位置三闭环控制，获取准确的动子位置是实现速度、位置环的基础;同时矢量控制中的坐标变换也需要知道动子位置。如果动子位置检测不正确，有可能会导致系统不能正常工作，甚至可能使电机产生振荡甚至过流等现象。采用的位置检测器件有:增量式光栅、绝对式光栅与霍尔传感器等。综合考虑成本与精度，采用最多的是增量式光栅。在位置环控制方面，一方面需要解决位置信号的准确计算问题;另一方面需要解决给定位置指令的精确跟踪问题。

光栅的分辨率越高，伺服控制系统的控制精度越好。但在极距长、光栅分辨率高的情况下，一个电周期内控制系统需要接收很多的脉冲，如果只采用一般性能的DSP芯片，则有可能超过控制系统计数器的最大值，导致位置信号不能准确计算，因而增加硬件是一种常用的解决方案，如采用的是计数芯片来存储电机位置信号［1］，优点是处理速度快，缺点是增加了系统成本。

伺服位置环用于实现电机跟随位置给定的曲线，从而实现位置指令的精确跟踪，其位置跟踪误差是衡量伺服系统的一个重要性能指标。国外在直线电机控制上应用了一些先进的算法［2-4］。国内在交流伺服系统数控机床上研究了减小轨迹跟踪误差的方法［5-7］。赵希梅等［8］提出一种较先进控制策略有效改善跟踪系能，但只是限于仿真研究。

针对以上两个问题，笔者在一个位置检测采用海德汉公司LS477增量式光栅(分辨率为0.5 μm)，控制系统采用TI公司的TMS320F2812控制芯片的永磁直线电机平台上进行研究，并提供有效解决方案。在位置计算方面，不采用计数芯片的方法，只利用软件偏差累加的方法实现角度的准确计算。在闭环跟踪方面，采用P+前馈复合控制的方法，并在实验上进行验证。

1 电机平台

直线电机试验平台如图1所示。

图1 直线电机试验平台

驱动对象是平板永磁直线电机，电机参数为:极距τ =24 mm，动子质量 m=50 kg，相电阻 R=2.3 Ω，Ld=32.98 mH，Lq=40.03 mH，永磁体磁链 Ψ =0.386 Wb。位置检测采用海德汉光栅尺LS477，其主要由光栅尺和读数头构成。

光栅尺LS477信号类型为增量式TTL信号，栅距为20 μm，读数头倍频数为10倍，经过倍频后的信号周期为2 μm，再经过DSP的内部QEP处理电路后，其测量步距为 0.5 μm，即直线电机每移动 0.5 μm，DSP内部寄存器T2CNT数值变化1。在实际的电机控制系统中，通过读取T2CNT的值以获得相应的动子位置角度，T2CNT与动子的角度对应关系如图2所示［9］。

图2 T2CNT与电角度对应关系

由图2可以看出，假设T2CNT增计数，直线电机移动一对极距所产生的脉冲数为Pulse_Count，寄存器T2CNT数值由0逐渐变化到T2PR=Pulse_Count，即电角度相对应的0°～360°。TMS320F2812的周期寄存器T2PR数据类型为Uint16最大计数为0xFFFF。试验平台的永磁直线同步电机一对极距为48 mm，产生的脉冲数Pulse_Count=96 000，已经超过了最大计数0xFFFF，因此上述的对应关系已不存在。本研究提出的解决方法是采用软件方法进行处理，而硬件上不增加额外硬件，只需要使用DSP内部自带的编码器采样计数模块。

2 动子位置计算

动子电角度的计算采用偏差累加的方法。由于DSP寄存器的数据类型为Uint16不能改变，程序中新定义一个int32的数据变量Total_PulseCount及Erro_PulseCount。程序的流程图如图 3所示。图 3中T2CNT为假设的增计数。在过零点判断时，根据图2中t1、t2处计数值 OldT2CNT和NewT2CNT，可得到脉冲差值为Erro_PulseCount=T2PR+NewT2CNTOldT2CNT。

对于动子初始位置的确定，本研究采用预定位方式，为防止定位失败，给定电机两个互相垂直的电压矢量，如使动子定位在A相轴线位置，则先后给定两个电压矢量，其位置为90°和0°，幅值为6 V，最终动子定位在0°电角度位置与A相相轴重合，定位成功。

试验平台的平板永磁直线同步电机在开环条件下1 Hz运行时，计算得到的电角度如图4所示。电机运行1 s的时间，所对应的电角度变化为0°～360°电角度，即一个电周期，对应于1 Hz。

图3 电角度计算流程图

图4 直线电机运行1 Hz条件下计算的电角度

3 伺服位置环控制原理

3.1 位置环原理框图位置角度

计算准确后，就可以进行速度、位置环的控制。位置环给定指令形式可以是:位移、角度、脉冲数，三者都是等效的［10］。位置环的原理框图如图5所示。本研究给定位置与电机的实际位置进行作差比较，然后采用PI控制器参与速度、电流环的控制中，令电机按照给定的位置进行移动。

3.2 P控制时位置跟踪误差分析

永磁直线同步电机位置环的等效传递函数框图如图6所示。其稳态误差为:

图5 位置环原理控制框图

式中:Go(s)—系统的开环传递函数，R(s)—系统的位置输入给定指令。

图6 位置环等效传递函数框图

在设计位置控制器时，一般把速度环等价为一个一阶惯性环节，直线电机机械模型已包含在速度环中，同时假设负载推力FL及直线电机的摩擦系数为零;一般令Kv=1，Kpp则由西门子的“最佳整定法则”确定一个较优值。

由式(1)可以看出，稳态误差与输入的指令形式有关。为了仿真不同输入指令形式的影响，基于Simulink搭建了永磁直线同步电机的数学模型。给定3种典型的输入指令，仿真了位置信号阶跃给定、斜坡给定与加减速给定时的位置响应，其位置跟踪误差曲线分别如图7～9所示。

图7 阶跃给定响应波形图

图8 斜坡给定位置跟踪误差曲线图

为防止直线电机运行过程中产生过冲，一般采用的是梯形加减速位置曲线，即加速-匀速-减速模式。

图9 加减速给定位置跟踪误差曲线图

由图7可以看出，在阶跃给定时随着比例系数的增大，系统的响应速度加快。由图7～9可以得出:随着比例系数的增大，位置跟踪误差逐渐减小，当然位置环比例系数不能无限制增大，否则会导致系统的不稳定。

3.3 P+前馈控制位置跟踪误差分析

P+速度前馈补偿控制策略的等效控制框图如图10所示。

图10 位置环前馈补偿等效传递函数框图

由图10可以得出系统的闭环传递函数为:

理想条件是令G(s)=1，那么电机的输出可以完全地跟随给定的指令，因此，可以得出F(s)的表达式为:

由式(3)可以看出前馈函数由两部分组成:一部分是速度前馈;另一部分为加速度前馈;系统的位置跟随误差传递函数为:

对于加减速位置给定曲线的匀速段，θ*(s)=v/s2，由此可得位置跟踪误差表达式为:

使用前馈补偿控制位置跟踪如图11所示。由式(5)可以看出随着前馈系数的增大，跟随误差会逐渐变小，与图11显示的仿真结果相吻合。由于仿真只采用了速度前馈补偿，对于匀速段的跟踪误差影响比较显著，匀速段误差影响较小，最后接近于零。

图11 使用前馈补偿控制位置跟踪误差

4 试验结果

实验时，由于直线电机长度有限，为方便调试及观察实验现象，让其做往复运动。直线电机往返运动给定曲线如图12所示。在图12显示的位置给定曲线中，正向运行的最大位置是120 mm;加减速段加速度a=48 mm/s，运行距离为S=24 mm;恒速段运行速度v=48 mm/s，运行距离S'=72 mm。往返运行时间总共为10 s。

图12 直线电机往返运动给定曲线

空载条件下的实验位置跟踪误差曲线图如图13、图14所示。从图中可以看出，随着比例系数的增大，位置误差减小，当增加到一定程度时，通过电机运行的实验现象可以看出电机明显运行不平稳，进一步增大会导致电机的振荡。因此采用前馈补偿在大大减小误差的前提下，最小的跟踪误差可以达到0.2 mm，电机还能稳定平稳地运行，达到了一个比较好的控制效果。

前馈补偿控制在负载条件下(拖动5 kg重物)的跟踪误差图如图15所示，局部放大图如图16所示，显然，随着前馈补偿系数的增加，跟踪误差逐渐变小，在Kv=10时跟踪误差达到了最小值，控制在±0.15 mm以内，但当Kv＞10时，跟踪误差又逐渐增大起来(如Kv=11的情况)，属于过补偿，不符合工程需要。因此，只要前馈系数选择得当，就能够大大缩小位置跟踪误差。

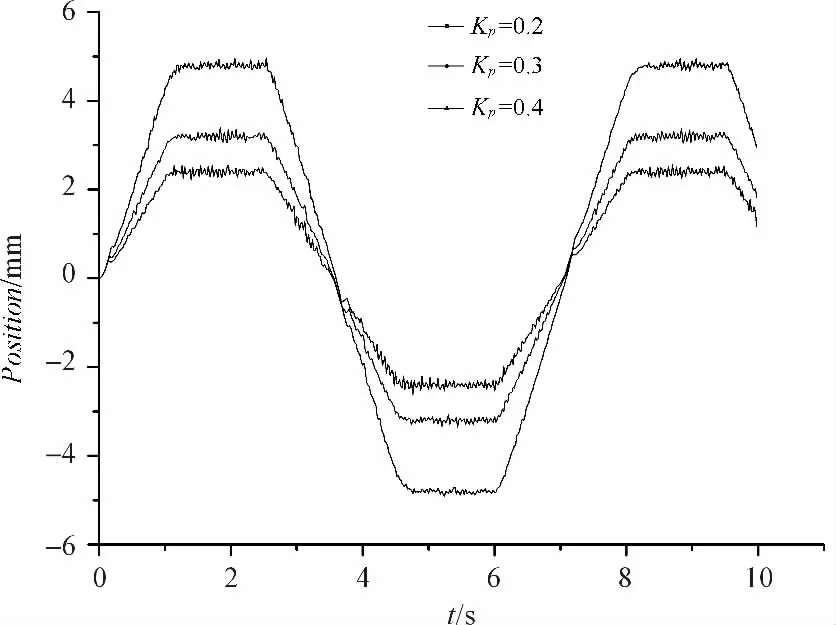
图13 空载单独采用P控制误差跟踪曲线

图14 空载采用前馈补偿控制

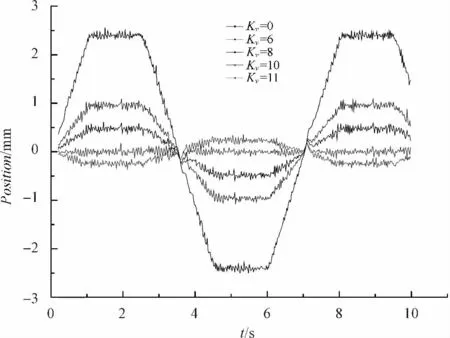
图15 负载采用前馈补偿控制

5 结束语

为了有效缩小位置跟踪误差，本研究针对永磁直线同步电机的位置环控制进行了相关研究:

(1)提出了通过软件方法处理动子电角度的计算，无需额外硬件且实现了动子角度的准确测量;

图16 Kp=0.4，Kv=10 位置跟踪误差

(2)位置环采用P+前馈控制算法，用来弥补单独采用P控制的不足，从而进一步减小了误差。

仿真与实验结果都表明，P+前馈补偿控制是一种减小跟踪误差的简单有效的方式，且无需复杂的编程。

［1］艾 武，刘凌云，张代林，等.LS7266R1在双轴位置信号检测中的应用［J］.仪表技术与传感器，2007(2):39-41.

［2］ALTER D M，TSAO T C.Optimal Feedforward Tracking Control of Linear Motors for Machine Tool Drives［C］.Proceedings of the Americal Control Conference，1995:210-214.

［3］OTTEN G，THEO J A，VRIES DE，et al.Linear motor motion control using a learning feedforward controller［J］.ASME Transactions on Mechatronics，1997，2(3):179-187.

［4］HOU BO-jie，GAO Jian-she，ZHOU Yun-fei.The Study of Feedforward Control Techniques of Linear Motor Guided by Air-bearing［C］.International Conference on Computer Distributed Control and Intelligent Enviromental Monitoring，2012:796-799

［5］滕福林，胡育文，黄文新，等.交流伺服系统位置跟踪误差［J］.南京航空航天大学学报，2008，40(6):815-819.

［6］金 钊，林宝君，冀群心.数控系统中伺服系统位置前馈控制器设计［J］.测控技术，2010，29(8):65-71.

［7］滕福林，李宏胜，吴爱萍，等.前馈控制对数控机床轮廓误差的影响［J］.组合机床与自动化加工技术，2011，11(11):22-25.

［8］赵希梅，郭庆鼎.最优ZPETC在高精度直线伺服跟踪控制中的应用［J］.沈阳工业大学学报，2006，28(1):49-53.

［9］高瑞昌，孙昌国.DSP在测速中的应用［J］.仪器仪表与检测技术，2004，23(3):71-73.

［10］秦 忆，周永鹏，邓忠华，等.现代交流伺服系统［M］.武汉:华中理工大学出版社，1995.