一种求解LP问题的两阶段基点迭代转移方法
2014-09-15刘道建黄天民
刘道建 ,黄天民,陈 勇
(1.西南交通大学 电气工程学院,四川 成都 610031; 2. 湖南科技大学 数学与计算科学学院,湖南 湘潭 411201)
当今,尽管学术界将LP算法划分成三大类型[1-4]:单纯形类算法、椭球类算法和内点类算法,但它们具有一个共同特征,即均属于迭代算法,根本区别在于迭代方式不同,这也导致了它们在搜索效率上的差异.单纯形类算法的优点在于迭代过程通过 “换基”实现,所以迭代运算均为线性的.缺点是在迭代过程中目标函数值的非严格单调性,当然,出现目标函数值的非严格单调性的内在因素在于退化基点的“一解多基”现象,这一缺陷可能导致迭代过程中的基循环问题.而椭球类算法与内点类算法却恰好相反,它们的优点是在迭代过程中目标函数值的严格单调性,缺点是主要的迭代运算是非线性的,每次迭代的计算量巨大.也正因为这一缺陷,虽然它们是多项式时间的,但实际使用效果并非十分理想,甚至搜索效率还不如单纯形类算法.那么,是否存在迭代运算为线性的,而迭代过程的目标函数值严格单调的LP算法?回答是肯定的,摄动单纯形法[1]就是这样的LP算法.
所谓摄动单纯形法,实为一种先将普通的LP问题转化为无退化现象的LP问题,再利用单纯形法求解的LP算法.从理论上看,摄动单纯形法是一种理想的LP算法,它同时具备上述提到的两个优良特性.然而,在实践中,因为摄动项的添加,相当于要解一个双倍于原LP问题规模的新问题,导致迭代过程的计算量呈爆炸性增长.因此,这种算法的实用性大大降低了.
线性、几何平面特性为线性规划的两大基本结构特性.椭圆类算法、内点类算法都是从非线性规划中移植过来的,属于非线性化方法.自然地,这些算法无法充分反映与利用好线性规划的以上两大结构特性.而传统的单纯形类算法(包括摄动单纯形法)的运算平台是单纯形表,该平台的线性特征十分明显,但几何平面特征明显不足,这也导致了传统单纯形类算法的功能缺陷.
鉴于以上情况,本文欲实现的主要研究目标如下:1)利用线性规划的结构特性,构建更能反映线性规划线性、几何平面这一两面性结构特点的LP新解算模型;2)从分析退化基点的转移机理入手,找到退化基点的转移性缺陷,并制定有效的应对之策;3)在以上两方面研究成果的基础上,提出迭代运算为线性、目标函数值严格单调的LP迭代算法,这也是本文欲达成的最终之研究目标.
1 单纯形基点的定向迭代转移模型
首先,本文研究对象为如下一般形式的LP问题:
MaxZ=cX,

(1)
其中,A1∈Rl×n,A2∈R(m-l)×n,by∈Rl×1,bz∈R(m-l)×1,c∈R1×n,且by≥0,bz>0.
引理1LP问题(1)与下列LP问题(2)等价:
MaxW=cX+0X′+0Y1-mY2,
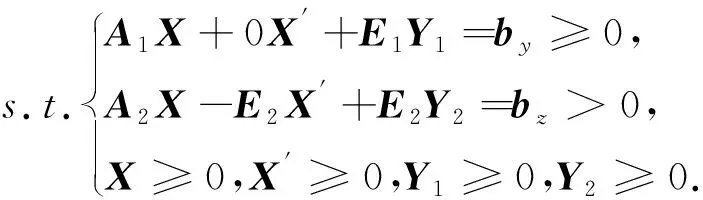
(2)
其中,E1∈Rn,E2∈Rm-l均是单位矩阵,m∈Rm-l,且m的所有元素都是无穷大正常数M.
定义1对于LP问题(1),将如下数字矩阵称之为它的初始基点定向转移矩阵:

(3)
而且,将它的如下三个分块:

(4)
分别称为该基点定向转移矩阵的基解块(列)、转移方向块和强迫性价值块(列),又将方向块的任意一列称为该矩阵的转移控制方向列,统称为转移控制矢量组(向量by,bz,m同上).
特别地,对于如下特殊的LP问题:
MaxZ=cX,

(5)
它的基点定向转移矩阵为:

对于LP问题(1)的如下约束不等式组:
引理2约束不等式组(6)有解当且仅当如下LP问题有最优解:
MaxW=0X+0X′+0Y1-mY2,
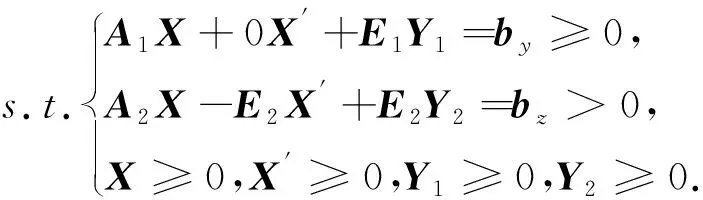
(7)
其中,E1∈Rn,E2∈Rm-l均是单位矩阵,m∈m-l,且m的所有元素都是无穷大正常数M.
定义2对于线性不等式组(6),将如下数字矩阵称之为它的初始基点定向转移矩阵:

(8)
而且,将它的如下三个分块:

(9)
分别称为该基点定向转移矩阵的基解块(列)、转移方向块和强迫性价值块(列),又将方向块的任意一列称为该矩阵的转移控制方向列,统称为转移控制矢量组,其中,向量by,bz,m与引理1中所定义的完全一致.
1)它们的基解块(列)表示单纯形(超多面体)的一个顶点A0;
2)它们的方向块之列向量代表过超多面体顶点A0的棱线方向.若以顶点A0为迭代点、这些棱线方向为迭代方向,则能够实现顶点A0向其邻近顶点的迭代转移;
3)它们的强迫性价值系数块(列)即代表顶点A0之优化转移的目标参考方向.
由此可见,借助基点定向转移矩阵,完全将LP的求解问题与线性不等式组的定解问题转化为同一类型的数学问题——矩阵优化转换问题.
为此,下面将针对基点定向转移矩阵之优化转换问题,引进一种特殊的矩阵变换——负旋转迭代运算.
定义3若基点定向转移矩阵的一个初等列变换同时满足如下条件:
1)它以基点定向转移矩阵中的某转移控制列的一个负元素为中心变换元素;
2)围绕中心变换元素,先经过矩阵列初等变换使中心变换元素变为1,在经过若干次矩阵列初等变换后使中心变换元素所在行的其他元素均变为零元素(强迫性价值列始终都不参与列初等变换);
3)在列变换过程中,要保持基解列的所有分量元素非负.则称这种特殊的矩阵初等变换为该基点定向转移矩阵关于转移控制列的一次负旋转迭代转换,同时把其中的中心变换元素称为该负旋转迭代变换的旋转主元(简称旋转元).
性质1如果基点定向转移矩阵的基解列是非退化的,那么,通过该矩阵关于转移控制组的任何一列元素(非负元素列除外)的负旋转迭代转移,一定可实现该基点向与之邻近基点的一次基点转移.
至此,通过构建单纯形(包括LP问题的可行域、线性不等式组的解空间)的基点定向转移矩阵,在单纯形的基点与数字矩阵之间建立起了一种对应关系.在矩阵的各功能块中,基解列代表基点,而其方向块的各列代表基点的迭代转移方向(即该超多面体顶点的极方向),强迫性价值系数列代表该基点转移的目标参考方向.本研究的目标之一在于,通过对基点定向转移矩阵的负旋转迭代(等价于基点的迭代转移),最终找到单纯形的一个优化极点.
实际上,依据上述性质1,仅解决了单纯形非退化基点的转移问题.要想利用基点定向转移矩阵的负旋转迭代运算来搜索单纯形的优化极点,还必须解决单纯形退化基点的转移问题.为此,引入下列定义及有关命题:
定义4若单纯形基点定向转移矩阵的基解列中所含零元素的个数大于决策变量数与剩余变量数之和,则称该基点定向转移矩阵对应的基点是退化的,将方向块中非单位行对应的基解列的零元素称为该基点的退化零元素,并称单纯形在该退化基点处具有局部非正则性.
定义5将“用无穷小量正参数ε替代退化基点的所有退化零元素”的操作称为一次单纯形局部小量正参数ε正则化;若单纯形的极点都是非退化的,则称该单纯形具有正则性(也称LP问题是正则的LP问题).
性质2只要小量正参数ε足够小,可行域的局部小量正参数ε正则化就不会改变LP问题的最优基.
性质3只要小量正参数ε足够小,经过局部小量正参数ε正则化的基点定向转移矩阵,不论通过多少次负旋转迭代运算,所得矩阵的ε零化矩阵(即,令其中的ε值为零而得到的矩阵)仍然为原LP问题的人工强迫性LP问题可行域基点的转移矩阵.
实际上,之所以要对单纯形进行局部小量正参数ε正则化处理,目的就是让可行域退化的基点非退化化,将退化基点的转移问题转化为非退化极点的转移问题,彻底消除基点退化对迭代搜索的不利影响.
基于以上非退化基点的定向转移矩阵及其转移性质、单纯形局部ε正则化、以及基点与矩阵的上述对应关系,针对LP问题(1),(5)或线性不等式组(6)的定解问题,构建如下单纯形基点的定向迭代转移模型:
上述点向式基点定向迭代转移模型清楚地表达了单纯形非退化可行基点之间的转移过程及转移机理.经过一次负旋转迭代运算,不仅将非退化顶点Ak转移到与之相邻的顶点Ak+1,而且,也将顶点Ak的转移控制方向组dj(Ak)(j=1,2,…,n)转换成顶点Ak+1的转移控制方向组dj(Ak+1)(j=1,2,…,n),为新基点Ak+1的转移创造了与旧基点Ak转移同样的条件.要利用单纯形极点转移进行寻优搜索,模型的这种属性是必须具备的,也是最基本的条件.
依据基点定向转移矩阵及其负旋转迭代的定义,不难得到如下定理:
定理1对于LP问题(1),设下列矩阵A0为它的基点定向转移矩阵:

(11)
如果存在一组矩阵{Hs|s=1,2,…,k}>(其中,Hs为A0的第s次负旋转迭代运算对应的初等变换矩阵),且令:

2)若W≤0,但v≠0,则LP问题(1)的解集必为空集,即LP问题(1)无最优解;

推论对于线性不等式组(6),设下列矩阵A0为它的基点定向转移矩阵:

(14)
如果存在一组矩阵{Hs|s=1,2,…,k}>(其中,Hs为A0的第s次负旋转迭代运算对应的初等变换矩阵),且令:
1)若W≤0,且v=0,则线性不等式组(6)的解集非空;
2)若W≤0,但v≠0,则线性不等式组(6)的解集必为空集.
2 两阶段基点迭代转移算法
2.1 基本思路与构想
先利用单纯形基点的定向迭代转移模型,从线性不等式组(6)的初始基点定向转移矩阵出发,通过负旋转迭代运算,求得线性不等式组(6)的一个可行基点及其基点定向转移矩阵,从而,利用这一矩阵,可以求得LP问题(1)的一个可行基点及其基点定向转移矩阵(它的基解列、转移控制列中不含人工变量值分量,而价值系数列中也不含强迫性无穷大正参数M),再利用单纯形基点的定向迭代转移模型求解之,最终求得原LP问题的最优解.新算法的整个寻优过程可分为如下两个阶段:
1)定解阶段:判断原LP问题的可行域(即约束不等式组的解空间)是否非空?
2)寻优阶段:在可行域非空的情况下,利用单纯形基点的定向迭代转移模型求出原LP问题的最优解.
2.2 所涉及的基本操作
为表述方便,不妨设当前需要操作的基点定向转移矩阵如下:
1)构建择优函数
根据前面的最优性判别定理,为确定极点的优化转移方向,可以构建如下择优函数:
ϑ(ζ)=c,ζ(ζ∈{aj|j=1,2,…,r}>).
(17)
2)选择迭代方向
根据上述择优函数(17),按照如下公式确定当前极点的优化转移方向ap:

(18)
显而易见,在aj(j=1,2,…,r)中,就是选择使择优函数值最大的向量做为当前极点的优化转移方向.
3)选择旋转主元
在当前极点的优化转移方向ap已被确定的情况下,依据前面负旋转迭代变换定义要求,就必须按照如下公式在ap中确定迭代运算的旋转主元aqp:
4)局部小量正参数ε正则化
假如当前极点出现退化的零元素,那么,在进行负旋转迭代变换之前,先把极点中的退化零元素全部替代为无穷小量参数ε,再利用上述(18)和(19)规则确定旋转主元,最后进行负旋转迭代运算.当搜索过程出现如下情形之一时,即可终止局部小量正参数ε正则化:
(a)在新极点对应的可行基解中,非零分量均已非含ε的无穷小量;
(b)新极点的转移控制矢量与目标向量的内积均小于或等于零(对目标函数极大化情形).
5)搜索终止条件
当ϑ(ak)≤0(∀ak∈{aj|j=1,2,…,r})时,最优(或定解)搜索立即终止.
2.3 基本步骤
利用新算法求解LP问题(1)的基本步骤如下:
步骤1 根据所给LP问题,确定它的约束不等式组的基点定向转移矩阵;
步骤2 判断当前矩阵的基解列中是否存在退化的零元素?是,用ε取代所有退化零元素;否,则进入下一步;
步骤3 判定当前基点定向转移矩阵是否符合定解终止条件?是,则进入下一步;否,则直接转入步骤五;
步骤4 根据前面定解定理,判定该约束不等式组是否有解?是,则直接转入步骤7;否,即可判定原LP问题无最优解,算法终止;
步骤5 利用所构建的选择函数,在当前基点的转移控制矢量组中选取一个目标优化方向矢;并进入下一步;
步骤6 利用负旋转迭代运算,求出比当前基点的目标函数值更优的基点的定向转移矩阵,并转入到步骤2.
(以上为定解阶段)
步骤7 利用当前基点定向转移矩阵,求出原LP问题的一个基点定向转移矩阵(它的价值系数列中不含强迫性无穷大正参数M),并进入下一步;
步骤8 判断当前矩阵的基解列中是否存在退化的零元素?是,用ε取代所有退化零元素;否,则进入下一步;
步骤9 判定当前基点定向转移矩阵是否符合定解终止条件?是,算法终止,并给出原LP问题的最优解,或者,判定原LP问题只有无界解;否,则转入下一步;
步骤10 利用所构建的选择函数,在当前极点的转移控制矢量组中选取一个目标优化方向矢;并进入下一步;
步骤11 利用负旋转迭代运算,找出比当前基点的目标函数值更优的基点之定向转移矩阵,并转入到步骤8.
(以上为寻优阶段)
3 实例展示
实例
解:
→
→
→
(以上为定解阶段,并由性质3可得如下第一个矩阵)
→
→
→
显然,此矩阵已符合终止条件,则:
标注在上述矩阵中,“*”表示省略元素后剩下的空格;x1,x2为决策变量,x3,x4分别为第5,6个条件约束的剩余变量,而x5~x8分别为第1~4个条件约束的松弛变量,y1,y2分别为第5,6个条件约束的人工变量.
对照分析新算法的运算平台为基点转移矩阵,相比单纯形类算法的运算平台——单纯形表, 基点转移矩阵这一新平台的结构化程度更高,不仅线性特征明显,而且几何平面特征也十分突出,更能反映LP模型之结构特点.另外,单纯形类算法之基点转移,因“换基”中的基退化问题而极易发生基循环现象.而利用新算法求解LP问题时,因为使用了可行域局部 -正则化方法处理基点退化转移问题,求解过程中的基点转移总在非退化情况下进行,所以,从根本上消除了基循环现象发生之可能.
4 结 论
1)在求解LP问题的过程中,由于新算法对退化极点采取了可行域局部小量正参数ε正则化处理,确保了整个寻优过程均在非退化情形下完成,消除了退化问题对极点迭代转移过程的不利影响,所以,新算法很好地解决了算法运行中的基循环问题.
2)新算法是以单纯形之极点的极方向为迭代方向的一种极点迭代算法,它采用择优函数确定迭代方向,并通过矩阵初等变换来实现极点的迭代转移,
操作简便快捷,便于程序化处理,避免了诸如椭圆法与内点法中繁杂的迭代运算,搜索效率显著提高.
3)基点定向转移矩阵作为新的LP问题算法平台,与传统的单纯形表比,它的结构化程度高,且充分反映了线性规划的几何平面特性,为解决LP的解算问题找到了一种新的数学工具.
4) 单纯形法是利用换基的方式来实现基点迭代转移的,转移过程极易受退化现象的影响(即易发生基循环问题).新算法的基点转移,本质上,已经回归到了传统的点向式转移方式,整个搜索过程始终在非退化的情形下完成,没有出现基循环的可能.
5)新算法的迭代运算是线性的,且迭代过程中目标函数值严格单调,但与摄动单纯形算法比较,它的计算量得到大大减少,所以,本研究基本达到了先期预设的研究目标.
6)对求解退化的LP问题,新算法继承了摄动单纯形算法的优点(即始终保持迭代中目标函数值的严格单调性),也克服了因摄动项的添加,使计算量猛然增加的缺陷.不过,与单纯形算法类似,新算法也存在变量爆炸性难题,这也是在今后研究中需要重点突破与解决的问题.
[1] 胡清淮,魏一鸣. 线性规划及其应用[M]. 北京:科学出版社,2004. 20-46.
HU Qing-huai, WEI Yi-ming. Linear programming and its application[M]. Beijing:Science Press, 2004. 20-46 .(In Chinese)
[2] DANTZIG G B. Linear programming extensions [M]. Princeton: Princeton University Press, 1963. 79-87.
[3] KHACHIYAN L G. A polynomial algorithm for linear programming [J].Soviet Mathematics Doklady, 1979, 20(3):191-194.
[4] KARMARKAR N K. A new polynomial-time algorithm for linear programming[J]. Combinatorica, 1984, 4(5):373-395.
[5] LI Wei. New variable of artificial-free algorithm for linear programming problem[J]. J of Math(PRC), 2008, 28(9): 243-248.
[6] 颜红彦,潘平奇. 线性规划的无比值检验Criss-Cross算法[J]. 合肥工业大学学报:自然科学版,2009,32(12):1949-1952.
YAN Hong-yan, PAN Ping-qi. Ratio-test-free criss-cross algorithm for linear programming[J]. Journal of Hefei University of Technology: Natural Science, 2009,32(12):1949-1952.(In Chinese)
[7] 刑金萍,樊彩霞. 改进的哈奇扬算法求解线性不等式组问题[J]. 科学技术与工程,2009,10(19):5752-5754.
XING Jin-ping, FANG Cai-xia. Improved khachiyan algorithm for systems of linear inequalities[J]. Science Technology and Engineering, 2009,10(19):5752-5754.(In Chinese)
[8] 曾梅清,田大钢. 线性规划问题的算法综述[J]. 科学技术与工程,2010,10(1):152-159.
ZENG Mei-qing, TIAN Da-gang. The review to the algorithm of linear programming problems[J]. Science Technology and Engineering, 2010,10(1):152-159.(In Chinese)
[9] 孙中波,段复建.不等式约束优化的非单调可行信赖域-SQP算法[J].应用数学学报,2011,34(4):655-670.
SUN Zhong-bo, DUAN Fu-jian. A feasible trust region SQP method with non-monotone line search for inequality constrained optimization[J]. Acta Mathematicae Applicatae Sinica , 2011, 34(4):655-670.(In Chinese)
[10] 刘道建, 黄天民. 一种线性不等式组的矩阵变换定解方法[J]. 上海交通大学学报:自然科学版,2012,46(10):1701-1706.
LIU Dao-jian, HUANG Tian-min. A matrix column-transform solution-decision method for the system of linear Inequalities[J]. Journal of Shanghai Jiaotong University : Natural Science, 2012, 46(10):1701-1706.(In Chinese)
