一种改进的数据流最大频繁项集挖掘算法*
2014-09-14吴毛毛
胡 健,吴毛毛
(江西理工大学信息工程学院,江西 赣州 341000)
一种改进的数据流最大频繁项集挖掘算法*
胡 健,吴毛毛
(江西理工大学信息工程学院,江西 赣州 341000)
提出了一种基于DSM-MFI算法的改进算法DSMMFI-DS算法,它首先将事务数据按一定的全序关系存入DSFI-list列表中;然后按排序后的顺序存储到类似概要数据结构的树中;接着删除树中和DSFI-list列表中的非频繁项,同时删除窗口衰退支持数大的事务项;最后采用自顶向下和自底向上的双向搜索策略来挖掘数据流的最大频繁项集。通过用例分析和实验表明,该算法比DSM-MFI算法具有更好的执行效率。
数据挖掘;数据流;界标窗口;最大频繁项集;窗口衰减支持数
1 引言
频繁模式的挖掘是关联挖掘的核心和基础[1],是影响挖掘算法效率的一个决定性的因素,它是产生关联规则的基础[2]。因此,在频繁模式[3~5]挖掘方面取得的任何进展都将对关联挖掘以至于其它数据挖掘任务的效率产生重要的影响。
由于最大频繁项集[6~9]中隐含着全部的频繁项集,因此可以将计算频繁项集的问题转化为计算最大频繁项集。在某些应用中,只需要最大频繁项集而并不需要所有的频繁项集,这样,研究直接计算最大频繁项集的算法显示出重要意义。
最近,数据库和数据挖掘继续集中到一个新的数据模型中,数据到达是以数据流的形式。在很多应用中,实时产生了大量的数据流,比如从一个传感器网络到另一个传感器数据传输产生的数据;各个连锁店事务数据的流入;Web记录和在Web上的点击流;在网络监控和交通管理的测量评估数据等[10]。本文就是基于这个背景提出了一个有效挖掘数据流中最大频繁项集的算法。
2 相关工作
Giannella C等人[11]提出了FP-stream算法来挖掘数据流上多个时间粒度的频繁模式,该方法应用倾斜时间窗口策略以精细的时间粒度保存数据流上最近的频繁模式信息,而以粗糙的时间粒度保存历史的频繁模式。马达等人[12]在一种基于压缩FP-树的最大频繁项集挖掘算法中提出一种剪枝策略并结合FP-树的结构,并根据Patricia-树的原理设计出PFP-树,对数据库进一步压缩降低内存。敖富江等人[13]提出一种新的基于文法顺序的FP-Tree的最大频繁项单遍挖掘算法FPMFI-DS,该算法采用混合搜索空间顺序策略,利用子集等级剪枝策略来压缩搜索空间的大小;同时提出了能够在线更新挖掘滑动窗口内数据流的最大频繁项集FPMFI-DS+算法。在界标窗口模型中,文献[14]提出了一种基于界标窗口模型的最大频繁项集的挖掘方法。S-FP-MFI算法[15]是一种基于FP树的改进的数据流最大频繁项集挖掘算法,它是根据条件模式基的项目数对条件模式基进行动态排序,用来减少函数调用的次数。基于事务矩阵挖掘最大频繁项集的方法AFMI[16]利用了迭代精简事务矩阵的方法来发现事务数据中的最大频繁项集,并提出了滑动窗口中的数据流最大频繁项集AFMI+算法。频繁模式树的约束最大频繁项集快速挖掘算法[17]能够删除不满足约束条件的项集,由于不需要生成候选项目集,所以效率很高。Li Hua-fu等人[18]首先提出的DSM-FI算法通过将事务数据存储到概要数据结构中,建立IsFI-forest,将每个项的投影子集存储到DHT表中,采用自顶向下的搜索策略来发现频繁项集。但是,该算法在删除一个非频繁项集时需要遍历整个项集前缀频繁项目森林(IsFI-forest),当森林结构复杂时,需要删除很多非频繁项集,需要很多次遍历森林,消耗的时间很多。对于较长的非频繁项集也要建立DHT表,同时要将各个子集投影到IsFI-forest中去,这样不仅使存储空间加大,而且还造成删除耗时。
本文提出的DSMMFI-DS(Dictionary Sequence Mining Maximal Frequent Itemsets over Data Streams)算法是基于DSM-MF算法[1]提出来的,DSMMFI-DS算法先对流入的数据流按一定顺序排序(本文是按一种全序关系)存入DSFI-list(Dictionary Sequence Frequent Item List)列表中,并且按这个顺序存储到DSSEFI-tree树中;接着删除DSFI-list列表中的非频繁项对应在DSSEFI-tree树中的项;然后删除DSFI-list列表中的非频繁项;最后在当前的概要数据结构中利用自顶向下和自底向上的双向搜索策略发现最大频繁项集。
3 问题的定义及相关知识
3.1 问题定义
从大的数据库中挖掘最大频繁项集是关联挖掘的一个重要问题。这个问题是Bayardo首先提出来的。问题的定义如下[1]:设Ψ={i1,i2,…,in}是一系列的数据,in称作项目。设数据库DB是一系列的交易事务,DB的大小用|DB|表示。一个事务T有m个项目,可以表示成T={i1,i2,…,im},k-项集就是包含有k个项目的集合,表示为{x1,x2,…,xk}。一个项目集X的支持度就是指在这个数据库中所有包含X项的总项目数占这个数据库项目总数的百分比,X项目的支持度用sup(X)表示。如果sup(X)>minsup,那么X就被称作频繁项集,minsup是用户自定义的最小支持度值,它的范围是[0,1]。所有频繁项集集合用FI(Frequent Item)表示。如果一个频繁项集不是任何一个频繁项集的子集,那么就把它叫做最大频繁项集,一系列最大频繁项集的集合用MFI(Maximal Frequent Itemsets)表示。本文目的就是找到所有支持度比用户给定的最小支持度大的最大频繁项集。
定义1[19]设数据流DS={w1,w2,…,wN},其中wi(∀i=1,2,…,N)的i是每一个基本窗口的标识,N是最后一个基本窗口的标识。它是一个连续的、无穷的基本窗口序列,每个基本窗口含有固定数目的事务,〈T1,T2,…,Tk,…〉,Tk={i1,i2,…,im},Tk(K=1,2,…)称为事务。
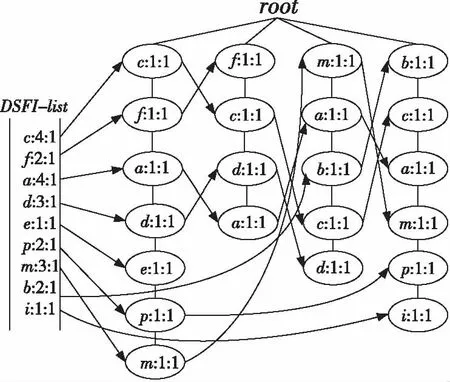
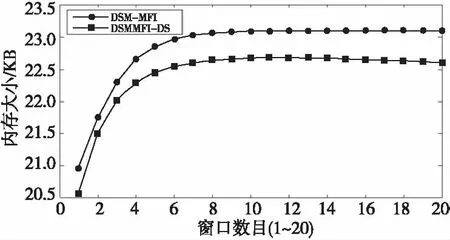
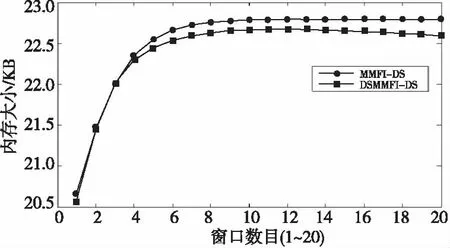
定义2设用户给定的支持度s和允许偏差ε(0<ε 3.2 窗口衰退支持数 由于数据流的流动性与连续性,在一段界标窗口内的事务数量可能很大甚至无限,数据流中蕴含的知识会随着窗口的推移而发生变化。而在实际的数据流应用中,最近产生事务所蕴含的知识往往要比历史事务的知识有价值得多。因此,在数据流频繁模式挖掘时,人们更希望挖掘出最近产生事务的频繁模式或者是最大频繁模式,而忽略那些历史事务的模式。 本文应用窗口衰减模型逐步衰减历史事务模式支持数的权重,并由此来区分新产生事务与历史事务的模式。如果记模式支持数在单位窗口内的衰退比率为衰减因子cf(0 (1) DSMMFI-DS算法先把每个窗口的事务数据存储到一个新的概要数据结构[19]—改进的前缀频繁项目树DSSEFI-tree中;然后根据DSFI-list列表中计算的每个项目的支持数,从DSSEFI-tree中删除不频繁项,接着删除DSFI-list列表中的非频繁项并将DSSEFI-tree树存储到DSSEFI-forest森林;最后根据用户需求或者需要遍历DSSEFI-forest森林挖掘相应项的最大频繁项集。 4.1 概要数据结构 为了适应滑动窗口内最大频繁项集的挖掘,本节设计了一种前缀概要项目树DSSEFI-tree,与DSM-MFI中的SFI-tree相比,除了存储项目名字item_name、窗口的标识window_count、项目的支持数node_count、指向DSFI-list表中的相同节点的指针node_link和指向DSSEFI-tree树中具有相同项目名字的节点item_brother外,还增加了一个参数就是窗口衰退支持数parameter,该参数主要记录着每个项随着窗口的移动所代表的权重,当parameter很大时说明该项不是最近窗口的项,我们可以尽早将该项从树结构中删除掉。 同时,为概要项目树DSSEFI-tree设计了一个头项列表DSFI-list,该列表与DSM-MFI算法中的FI-list相比,除了具有存储项目名字item_name、窗口的标识window_count、项目的支持数node_count、指向DSSEFI-tree树中的相同节点的指针node_link和指向DSSEFI-tree树中具有第一个相同项目名字的节点item_brother外,也增加了窗口衰退支持数parameter,由这个参数我们就可以很快知道树中存储的哪些项是已经过期的,可以很方便地将此项删除。 4.2 增量更新DSSEFI-tree树 由于数据流不断地流入,内存的存储空间有限,需要实时地对树进行更新,及时删除不频繁项集和过期的项,同时要及时返回用户查询的结果。由于树本身在存储时是按照头项列表中的全序关系进行存储的,不受项到来的先后顺序影响,在对项进行操作时也比较方便。再根据用户设定的最小支持度和窗口衰退支持数阈值,在每一个窗口到来之后就对树进行一次更新,这样可以很快地将树中的不频繁项集和已经过期的项集剪枝掉,在节省内存空间的同时提高了查询的效率。假设新的窗口事务数据TDS(i)=(a1,a2,…,aN)到来时,算法1是对树DSSEFI-tree的更新。 算法1增量更新树DSSEFI-tree 输入:事务数据TDS(i)=(a1,a2,…,aN),用户设定的最小支持度s,用户设定的窗口衰退支持数阈值p,用户允许的最大误差率ε(0,s); 输出:更新后的树DSSEFI-tree。 (1) ifDSFI-list=∅,then {window_count=1; (2)foreachaj,将aj的item_name、window_count和node_link插入到DSFI-list中; (3)endfor (4) 为树DSSEFI-tree构造根节点root; (5)foreachaj,将aj的item_name、window_count、node_count、node_link、item_brother和parameter插入到DSSEFI-tree中;} (6)endfor (7)endif (8)else{ window_count=i; (9)foreachaj按全序插入到DSFI-list中; (10) if有相同item_name的项itemthenitem.parameter=aj.parameter; (11)endif (12)foreachDSFI-list中的每个项ai对应的parameter项进行更新:parameter=cf(P,Ti-1)×cf+c; (13)ifai.parameter≥p,将ai从树DSSEFI-tree中删除,接着从DSFI-list中删除; (14)endif (15)ifai.node_count (16)endif (17)endfor (18)endfor (19)} (20)}endelse 4.3 最大频繁项集的挖掘算法 更新完树DSSEFI-tree后,我们根据需求来对数据流进行操作,查找相应项的最大频繁项集。本文设计一个改进的双向搜索策略tb-btMFI(top-bottomandbottom-topselectionofMaximalFrequentItems)[20],双向搜索从DSSEFI-tree树中发现最大频繁项集,其中设计一个监控参数monitor,让自顶向下搜索和自底向上搜索同步进行,可以及早发现不频繁项,提高挖掘效率。 算法描述:自顶向下搜索,设置monitor的值为0,对每一个项x,将x所在的最长路径中所有项合并形成最大频繁候选项集存储在M1中(假设为k项集),对这个最长的项集进行支持度计算,如果它满足用户给定的最小支持度,则它是最大频繁项集,并将这个最大频繁项集加入到MFI中,令monitor为1,转到自底向上搜索,如果M2中某项是MFI的子集,则从M2删除此项;如果不满足,则对x和其他项进行任意组合形成k-1项集存储在M1中,令monitor为1,转到自底向上搜索,如果M2中某项是MFI的子集则从M2删除此项。依次进行下去,直到M1为空为止。自底向上搜索,如果monitor的值为1,从树的叶子节点开始对x项进行相邻两短项集组合,存储在M2中,搜索到L层时仍然保留L-1层中的项,然后对组合的项集进行支持度计算,对第L层上的某个项目集X,若X是MFS中某频繁项目集的子集,则不对X进行支持度计算,令monitor的值为0,转到自顶向下搜索;否则,对X进行支持度计算,若X是第L层中的频繁项目集,则从M2中删除X在L-1层中的所有项目子集,否则删除X,令monitor的值为0,继续自顶向下搜索;若第L-1层中的某个频繁项目集y在第L层上的所有超集均为非频繁项目集,则将y加到MFS中并从M2中删除y,令monitor值为0,继续自顶向下搜索。如果monitor的值为1,则处理完第L层上的每一个项目集,如果monitor的值为1,则生成L+1层上的候选频繁项目集,依次类推,直到M2为空。如算法2所示。 算法2tb-btMFI算法 输入:更新后的DSSEFI-tree树,当前窗口标识N,最小支持度s,用户允许的最大误差率ε; 输出:最大频繁项集MFI。 (1)令MFI=∅,M1=∅,M2=∅,monitor=0; (2)for(k=n;k≥1;k--) (3){ (4)M1={路径中包含Xi项目的组成最大候选频繁项集X}; (5) 计算各候选频繁项集的支持度; (6)if候选项集∈MFIthenM1=M1-X,monitor=1,转到(13); (7)else计算候选项集X的支持度; (8)ifX.node_count≥s·X.SLorX.node_count<ε·X.SLthen (9) MFI=MFI∪{X},monitor=1,转到(13); (10)elseM1=M1-{X},monitor=1,转到(13); (11)} (12)ifM1={∅}then退出; (13)for(k=0; k<=L; k ++){ (14)M2={包含xi项的相邻两项组成的候选频繁项集X} (15)ifX∈MFIthen (16)M2=M2-X,monitor=0,转到(2); (17)if在第k-1层的项X是第k层的子集then (18)M2=M2-X,monitor=1,转到(2); (19) 计算各项目X的支持度; (20)ifX.node_count≥ s·X.SLorX.node_count< ε·X.SLthen (21) MFI=MFI∪{X},monitor=1,转到(2); (22)elseM2=M2-X,monitor=1,转到(2); (23)} (24)ifM2={∅}then退出; (25)endfor 5.1 算法的复杂性分析 (1)时间复杂度。 (2) 对于MMFI-DS算法:(1)在SEFI-tree构造和维护算法中,算法需把T×N个项目插入到SEFI-tree中,删除一个不频繁项目,算法需删除此不频繁项在EIS-tree中节点的个数,设其数目为C3。(2)在发现最大频繁项集的算法中,MMFI-DS算法的时间复杂度为[19]: T×N+C1×C3+C2× (3) 对于DSMMFI-DS算法:(1)在DSSEFI-tree树的增量更新中,算法也要把T×N个项目插入到DSSEFI-tree中,删除一个不频繁项目,算法需删除此不频繁项在DSSEFI-tree中节点的个数,设其数目为C4。(2)在发现最大频繁项集的算法中,DSMMFI-DS算法的时间复杂度为: T×N+C1×C4+C2× (3) (2)空间复杂度。 DSM-MFI算法在内存中需要保存FI-list表、OFI-list表和SFI-tree树;MMFI-DS算法在内存中需要保存FI-list表、OFI-list表和EIS-tree树;DSMMFI-DS算法在内存中保存DSFI-list表和DSSEFI-tree树。DSM-MFI算法和MMFI-DS算法都用了投影子集的方法,将投影子集项存放在OFI-list表中,这样占用了一定大小的内存空间,DSMMFI-DS算法用DSFI-list表来存放频繁一项集,一方面,不需要存储每个项目的投影子集,就节省了内存的空间,另一方面因用DSSEFI-tree树结构的存储经过全序排序后树的分支少,结构简单,同时在节点数据域中增加了监控参数monitor,这样可以尽早地删减已经过期的或者对用户没有意义的频繁项,从而更节省了内存的开销。假设频繁1-项目的树为k,DSM-MFI算法需要存储2k个节点,MMFI-DS算法需要存储C×k(C为常数)个节点,DSMMFI-DS算法则需要存储C×r个节点(r为k个频繁项集删除过期或者用户不感兴趣的项后剩下的频繁项目树r≤k),显然,C×r≤C×k<2k,所以DSMMFI-DS算法比DSM-MFI算法和MMFI-DS算法在相同环境中处理同样数据流更节省内存空间。 5.2 用例分析 假设某一数据流W1=[c,f,a,d,e,p,m;f,c,d,a;m,a,b,c,d;b,c,a,m,p,i],从窗口中读入完数据存储到DSFI-list中的结构。 如图1所示,假定用户给定的最小支持度为3,从DSFI-list中删除,然后根据DSFI-list列表中的顺序存储到DSSEI-tree中的结构,如图2所示。 同样地用DSM-MFI算法得到的SFI-tree树存储结构如图3和图4所示。 Figure 1 Tree storage structure of DSSEFI-tree after DSMMFI-DS algorithm reads the data streams图1 DSMMFI-DS算法读取完数据流后 DSSEFI-tree树存储结构 Figure 2 Tree storage structure of DSSEFI-tree after DSMMFI-DS algorithm removes not frequent itemsets图2 DSMMFI-DS算法删除不频繁项集后的 DSSEFI-tree树存储结构 Figure 3 Tree storage structure of SFI-tree after DSM-MFI algorithm reads the data streams图3 DSM-MFI算法读取完数据流后 SFI-tree树存储结构 Figure 4 Tree storage structure of SFI-tree after DSM-MFI algorithm removes not frequent itemsets图4 DSM-MFI算法删除非频繁项集后的 SFI-tree树存储结构 从上面的结构图我们可以看到,MMFI-DS算法由于没有对读入的数据流进行排序,那么它的有些计数少的项目存储到EIS-tree树中可能成为根节点,这样我们在用自顶向下的算法搜索时发现最大频繁项集时会花费更多的时间来计算项目的支持度;另一方面,由于没有进行排序,那么频繁项目在存储时可能分布在树的各个分支中,这样在存储空间方面又会造成浪费。在DSM-MFI算法里,不但要存储IsFI-forest,而且还要存储每个项的投影子集,在同样多的事务数据下需要更多的内存来存储。而DSMMFI-DS算法在读入时对项目按一定的顺序排序后,那么它们共享的前缀个数就多了,使树的存储结构得到了简化,节省了存储空间;另一方面,在挖掘最大频繁项集时也由于共享的前缀个数多,所以会在较短的时间里发现最大频繁项集。 实验在CPU为Intel Pentium(R) Dual-Core 3.20 GHz、内存为2.00 GB、操作系统为Windows 7 Ultimate的PC机上进行,所有的实验程序均采用Visual C++ 6.0实现。实验中的模拟数据由IBM数据生成器产生,为了符合数据流产生的特点,我们设定产生10 000 k条数据项,其中1 k表示1 000条数据项,同时我们设定每个窗口的事务数据以及其他所有参数都使用默认值。用户设定的最小支持数为0.1%,最大允许误差ε固定为0.1Xs。对DSM-MFI和DSMMFI-DS两种算法执行时的时间和占内存空间进行比较,图5显示DSMMFI-DS算法比DSM-MFI算法的执行时间要少,一方面DSMMFI-DS算法不需要为每个项建立投影,另一方面在发现最大频繁项集时DSMMFI-DS采用双向搜索策略,所以DSMMFI-DS算法比DSM-MFI算法的执行效率要高。图6显示DSMMFI-DS算法比DSM-MFI算法在运行时所占的内存空间要小,特别是在随着窗口数目增多时,这种效果更明显: (1)DSM-MFI需要为每个项做投影,内存需要存储每个项的投影子集; (2)每个项在建立相应的树时没有进行排序,那么树的分支也会比较多,存储时需要更多的内存空间; (3)DSMMFI-DS算法会根据每个项的窗口衰减支持数,及时将支持数小的项删除。因此,DSMMFI-DS算法所占的内存空间比DSM-MFI要小。 Figure 5 Execution time of DSM-MFI algorithm and DSMMFI-DS algorithm图5 DSM-MFI算法和DSMMFI-DS算法执行时间 Figure 6 Memory of DSM-MFI algorithm and DSMMFI-DS algorithm图6 DSM-MFI算法和DSMMFI-DS算法存储内存 MMFI-DS算法也是对DSM-MFI算法的改进,为了验证MMFI-DS算法和DSMMFI-DS算法的优越性,也对MMFI-DS算法进行了实验对比。如图7和图8所示。 Figure 7 Execution time of MMFI-DS algorithm and DSMMFI-DS algorithm图7 MMFI-DS算法和DSMMFI-DS算法执行时间 Figure 8 Memory of MMFI-DS algorithm and DSMMFI-DS algorithm 图8 MMFI-DS算法和DSMMFI-DS算法存储内存 通过实验可以看出,DSMMFI-DS算法比MMFI-DS算法的执行效率更高。在图7中,由于DSMMFI-DS算法采用的是全序关系存储数据,与数据到来的时间顺序没有关系,在存储上更节省时间;而MMFI-DS算法没有按一定的顺序存储,在进行挖掘操作时需要花费很多时间来搜索。在图8中,在窗口数目比较小时,MMFI-DS算法和DSMMFI-DS算法的存储空间相差不大,但是随着窗口数目的不断增多,DSMMFI-DS算法更具有优越性,占用的内存空间小,主要是因为DSMMFI-DS算法能够及时地将不频繁项集从树中删除。 本文提出了改进的界标窗口内数据流最大频繁项集挖掘算法DSMMFI-DS,该算法采用了按全序排序存储,不需要对每个项进行投影,并存储投影子集;该算法在发现最大频繁项集时采用自顶向下和自底向上的双向搜索策略,能快速发现最大频繁项集,最后该算法存储每个项的窗口衰退支持数,根据设定的窗口衰退支持数阈值能够尽早地删除那些支持数小的项,节省了内存空间。通过实验得出DSMMFI-DS算法比DSM-MFI算法和MMF-DS算法具有更好的执行效率。 [1] Li H, Lee S, Shan M. Online mining (recently) maximal frequent itemsets over data streams[C]∥Proc of the 15th International Workshops on Research Issues in Data Engineering:Stream Data Mining and Applications, 2005:11-18. [2] Han J,Kamber M.Data mining:Concept and techniques[M].2nd edition. San Fransisco:Higher Education Press, 2001. [3] Pan Yun-he,Wang Jin-long,Xu Cong-fu.State of the art on frequent pattern mining in data streams[J].Acta Automatica Sinica, 2006,32(4):594-602. (in Chinese) [4] Meng Cai-xia. Research on mining frequent itemsets in data streams[J].Computer Engineering and Applications, 2010,46(24):138-140. (in Chinese) [5] Zhuang Bo,Liu Xi-yu,Long Kun.TWCT-stream:Algorithm for mining frequent patterns in data streams[J]. Computer Engineering and Applications, 2009,45(20):147-150. (in Chinese) [6] Yan Yue-jin.Research on mining algorithms of maximal frequent item sets[D]. Changsha:National University of Defense Technology,2005. (in Chinese) [7] Yan Yue-jin, Li Zhou-jun, Chen Huo-wang. A depth-first search algorithm for mining maximal frequent itemsets[J].Journal of Computer Research and Development, 2005,42(3):462-467. (in Chinese) [8] Huang Shu-cheng,Qu Ya-hui.Survey on data stream classification technologies[J].Application Research of Computers, 2009,26(10):3604-3609. (in Chinese) [9] Ji Gen-lin,Yang Ming,Song Yu-qing, et al.Fast updating maximum frequent itemsets[J].Chinese Journal of Computer, 2005,28(1):128-135. (in Chinese) [10] Li Hua Fu,Lee Suh Yin.Mining frequent itemsets over data streams using efficient window sliding techniques[J].Expert Systems with Applications, 2009,36(2,Part 1):1466-1477. [11] Giannella C, Han Jia-wei, Pei Jian, et al. Mining frequent patterns in data streams at multiple time granularities[M]∥Data Mining:Next Generation Challenges and Future Directions,Cambridge:MIT, 2003. [12] Ma Da,Wang Jia-qiang.A compressed FP-tree based on algorithm for mining maximal frequent itemsets[J].Journal of Changchun University of Science and Technology(Natural Science Edition), 2009,32(3):457-461. (in Chinese) [13] Ao Fu-jiang,Yan Yue-jin,Liu Bao-hong, et al.Online mining maximal frequent itemsets in sliding window over data streams[J].Journal of Sytem Simulation, 2009,21(4):1134-1139. (in Chinese) [14] Li Hai-feng,Zhang Ning. Maximal frequent itemsets mining method over data stream[J].Computer Engineering, 2012,38(21):45-48. (in Chinese) [15] Hu De-min, Zhao Rui-ke. An improved algorithm for mining maximum frequent itemsets[J].Computer Applications and Software, 2012,29(12):186-188. (in Chinese) [16] Zhang Yue-qin, Chen Dong. Mining method of data stream maximum frequent itemsets[J].Computer Engineering, 2010,36(22):86-90. (in Chinese) [17] Hua Hong-juan, Zhang Jian, Chen Shao-hua. Mining algorithm for constrained maximum frequent itemsets based on frequent pattern tree[J].Computer Engineering, 2011,37(9):78-80. (in Chinese) [18] Li H, Lee S, Shan M. An efficient algorithm for mining frequent itemsets over the entire history of data streams[C]∥Proc of the 1st International Workshop on Knowledge Discovery in Data Streams, held in conjunction with the 15th European Conference on Machine Learning (ECML 2004) and the 8th European Conference on the Principles and Practice of Knowledge Discovery in Databases (PKDD 2004), 2004:1. [19] Mao Yi-min,Yang Lu-ming,Li Hong, et al. An effective algorithm of mining maximal frequent patterns on data stream[J]. Chinese High Technology Letters, 2010,3(3):100-107. (in Chinese) [20] Song Yu-qing,Zhu Yu-quan,Sun Zhi-hui, et al.An algorithm and its updating algorithm based on FP-tree for mining maximum frequent itemsets[J].Journal of Software, 2003,14(9):1586-1592. (in Chinese) 附中文参考文献: [3] 潘云鹤,王金龙,徐从富.数据流频繁模式挖掘研究进展[J].自动化学报,2006,32(4):594-602. [4] 孟彩霞.面向数据流的频繁项集挖掘研究[J].计算机工程与应用,2010,46(24):138-140. [5] 庄波,刘希玉,隆坤.TWCT-Stream:数据流上的频繁模式挖掘算法[J].计算机工程与应用,2009,45(20):147-150. [6] 颜跃进.最大频繁项集挖掘算法的研究[D].长沙:国防科学技术大学,2005. [7] 颜跃进,李舟军,陈火旺.一种挖掘最大频繁项集的深度优先算法[J].计算机研究与发展,2005,42(3):462-467. [8] 黄树成,曲亚辉.数据流分类技术研究综述[J].计算机应用研究,2009,26(10):3604-3609. [9] 吉根林,杨明,宋余庆,等.最大频繁项目集的快速更新[J].计算机学报,2005,28(1):128-135. [12] 马达,王佳强.一种基于压缩FP-树的最大频繁项集挖掘算法[J].长春理工大学学报(自然科学版),2009,32(3):457-461. [13] 敖富江,颜跃进,刘宝宏,等.在线挖掘数据流滑动窗口中最大频繁项集[J].系统仿真学报,2009,21(4):1134-1139. [14] 李海峰,章宁.数据流上的最大频繁项集挖掘方法[J].计算机工程,2012,38(21):45-48. [15] 胡德敏,赵瑞可.一种改进的最大频繁项集挖掘算法[J].计算机应用与软件,2012,29(12):186-188. [16] 张月琴,陈东.数据流最大频繁项集挖掘方法[J].计算机工程,2010,36(22):86-90. [17] 花红娟,张健,陈少华.基于频繁模式树的约束最大频繁项集挖掘算法[J].计算机工程,2011,37(9):78-80. [19] 毛伊敏,杨路明,李宏,等.一种有效的数据流最大频繁模式挖掘算法[J].高技术通讯,2010,3(3):100-107. [20] 宋余庆,朱玉全,孙志挥,等.基于FP-Tree的最大频繁项目集挖掘及更新算法[J].软件学报,2003,14(9):1586-1592. HUJian,born in 1967,PhD,professor,his research interests include knowledge engineering and knowledge discovery, and software engineering. 吴毛毛(1987-),男,江西鹰潭人,硕士生,研究方向为数据挖掘。E-mail:wumaomao2010@163.com WUMao-mao,born in 1987,MS candidate,his research interest includes data mining. Animprovedalgorithmforminingmaximalfrequentitemsetsoverdatastreams HU Jian,WU Mao-mao (Institute of Information Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China) Based on the algorithm of DSM-MFI, an improved algorithm, named DSMMFI-DS (Dictionary Sequence Mining Maximal Frequent Itemsets over Data Streams), is proposed. Firstly, it stores transaction data into DSFI-list in alphabetical order. Secondly, the data are stored sequentially into the tree similar to the summary data structure. Thirdly, non-frequent items in the tree and DSFI-list are removed, and the transaction items with the maximum count of window attenuation supports are deleted. Finally, the strategy (top-down and bottom-up two-way search) is used to mine maximal frequent itemsets over data streams, and case analysis and experiments prove that the algorithm DSMMFI-DS has better performance than the algorithm DSM-MFI. data mining;data stream;landmark windows;maximal frequent itemsets;window attenuation support count 1007-130X(2014)05-0863-08 2012-12-03; :2013-04-03 TP274.2 :A 10.3969/j.issn.1007-130X.2014.05.030 胡健(1967-),男,江西赣州人,博士,教授,研究方向为知识工程与知识发现、软件工程。E-mail:1050023437@qq.com 通信地址:341000 江西省赣州市客家大道156号 Address:156 Kejia Avenue,Ganzhou 341000,Jiangxi,P.R.China4 算法描述
5 算法的复杂性分析与用例分析

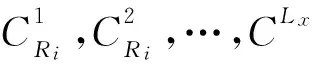



6 实验结果和分析


7 结束语


