基于非线性变换的自适应时间延迟估计
2014-09-14刘文红郭冬梅邱天爽
刘文红, 雷 鹏, 张 帅, 郭冬梅, 邱天爽
(1. 上海电机学院 a. 电子信息学院, b. 电气学院, 上海 201306;2. 大连医科大学附属第二医院 放射科, 辽宁 大连 116027;3. 大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024)
基于非线性变换的自适应时间延迟估计
刘文红1a, 雷 鹏1b, 张 帅1b, 郭冬梅2, 邱天爽3
(1. 上海电机学院 a. 电子信息学院, b. 电气学院, 上海 201306;2. 大连医科大学附属第二医院 放射科, 辽宁 大连 116027;3. 大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024)
含有脉冲性噪声的信号常使经典的时间延迟估计算法效果变差。给出了一种基于Sigmoid变换的自适应时间延迟估计算法(SATDE),采用Sigmoid函数,对含有脉冲性噪声的信号进行非线性变换;利用自适应滤波器对信号的时间延迟参量进行估计。计算机数值仿真实验结果表明,该算法在对信号的时间延迟进行估计时,不仅可以适用于符合高斯模型的信号噪声,更适用于含有脉冲噪声的信号。该算法是一种具有较好鲁棒性的时间延迟估计算法。
时间延迟估计; 自适应滤波; 脉冲性噪声; 非线性变换; Sigmoid函数
信号的时间延迟通常是指同源信号之间由于传输信道的差异和/或传感器的接收距离不同而引起的到达时间差。时间延迟是表征信号的一个基本参量,可以利用参数估计及信号处理的理论技术和方法,对上述时间延迟进行估计,并由此进一步确定其他有关参数,如,信道的结构特点和温度,信源目标的距离、方位、运动方向和速率等。对时间延迟及其有关参量估计的研究,一直是信号处理领域中一个比较活跃的研究课题,它具有比较重要的理论意义和较广的应用价值,在地质勘探、故障诊断、无线电定位、雷达、声纳、通信及生物医学等领域都得到了广泛的应用[1-5]。
在实际应用中,采集的信号往往含有噪声,这些噪声的特点并不相同。应用概率统计理论进行信号处理,通常会涉及如何利用概率模型来描述观测信号和噪声的问题。而这种信号和噪声的概率模型通常是所需信息的函数,信息通常由一组参数构成。这组参数通过某种优化准则从观测数据中提取出来。显然,用这种方法从数据中得到所需信息的精确程度主要取决于所采用的概率模型和优化准则。一个好的统计模型应该与实际信号相符合,且便于分析处理[6-8]。
在传统的信号处理中,高斯模型占据了主导地位。它是许多背景噪声的概率模型。然而,在实际应用中还存在不少非高斯信号及噪声,如水声信号、生物医学信号、低频大气噪声、金融数据以及许多人为产生的信号与噪声等,且带有明显的脉冲性;同时,在获得数据的过程中,常常会出现一些未被注意或难以察觉的意外情况,使数据中不可避免地或多或少地含有反常数值。α稳定分布是一种描述脉冲信号和噪声的统计模型。信号和噪声的非高斯脉冲特性,常引起基于高斯假定所设计的最优信号处理系统的性能显著退化。当这种性能退化达到一定程度而不能被容忍时,就必须根据信号和噪声的统计特性重新设计新型的具有鲁棒性的处理算法[9-12]。
对数据进行适当的非线性变换是一种鲁棒性的处理算法,如神经网络中常用的Sigmoid函数就是一种非线性函数[13-14]。本文给出了一种基于Sigmoid变换的自适应时间延迟估计算法(Sigmoid Adaptive Time Delay Estimation, SATDE)。该算法采用Sigmoid函数对信号和噪声进行非线性变换,抑制了脉冲噪声或反常数值对估计结果的影响;再结合自适应滤波器,对信号进行时间延迟的估计。
1 基于Sigmoid变换的自适应时间延迟估计算法
1.1Sigmoid变换
神经网络中常用一种非线性函数——Sigmoid函数作为信息传递函数。Sigmoid函数的数学表达式如下:
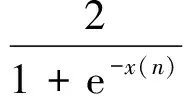
(1)
式中,n为离散时间变量。Sigmoid函数曲线如图1所示。

图1 Sigmoid函数曲线Fig.1 Curve of sigmoid function
Sigmoid函数是一种非线性变换,它具有光滑、单调有界的特性。该函数对不同幅度的信号、噪声的非线性作用不同,实际应用中,主要考虑信噪比的大小,而不是信号、噪声的绝对幅度。Sigmoid函数对输入信号中较大的值有抑制作用,是一种非线性变换;对输入信号中较小的值,则近似线性变换,因此,比较适合用来对带有脉冲性噪声的信号进行非线性变换,并在抑制脉冲性噪声或明显不合理数据的同时,保留原信号的有用信息。本文用特征指数α=1.5的对称α稳定分布(简称SαS)进行脉冲性信号噪声建模,然后经过Sigmoid变换。图2给出了Sigmoid变换前、后的对称α稳定分布(α=1.5)的波形。其中,n为样本点。
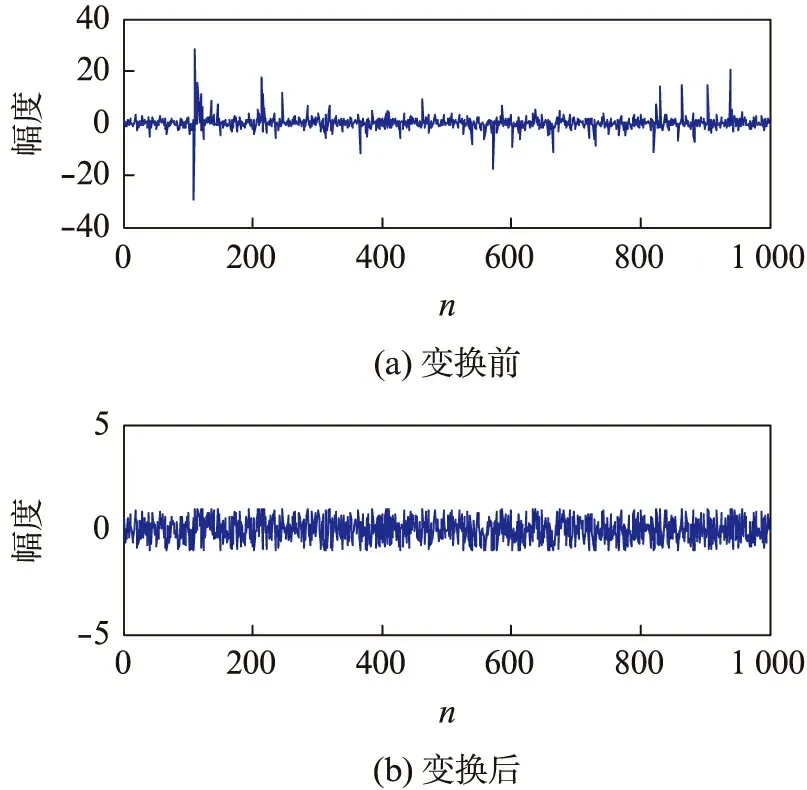
图2 Sigmoid变换前、后的对称α稳定分布(α=1.5)波形Fig.2 Waveforms of SαS with α=1.5 before andafter sigmoid transformation
由图可见,脉冲性信号噪声经过Sigmoid变换后,去除了其中的尖峰脉冲或不合理的数值。
1.2自适应滤波器
与一般的滤波器不同,自适应滤波器能够根据某种优化准则,通过迭代自动地调整滤波器的参数,以适应变化的环境,故自适应滤波器得到了广泛应用。
根据结构不同,自适应滤波器主要可分为横向、格型自适应滤波器以及递归型自适应滤波器等[13]。目前,应用最多的是横向自适应滤波器及其最小均方误差自适应算法。图3给出了单输入横向自适应滤波器的结构图[15]。
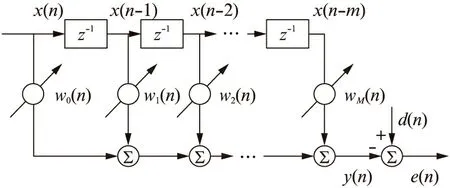
图3 单输入横向自适应滤波器的结构图Fig.3 Structure of single input transversal adaptive filter
图中,自适应滤波系统的输入信号为x(n),其中,z-1表示一个采样间隔的延迟;d(n)为参考信号;wm(n)(滤波器价数m=0,1,…,M)为自适应滤波器的加权系数;e(n)为误差信号;y(n)为该系统的输出信号。e(n)被反馈回来后用做自适应滤波器权系数调节的控制信号。通常,调整加权系数,系统的输出信号y(n) 逐渐接近参考信号d(n),两者误差的均方值逐渐减小。当自适应滤波器收敛时,e(n)的均方值达到最小,输入信号x(n)经过自适应滤波器在均方误差意义上最接近d(n)。均方误差函数是凸函数,在其导数为零处有最小值,该处对应的权系数就是最优值;可以采用最速下降法通过迭代来寻找其最小点,即沿着该函数梯度下降最大的方向来调整加权系数,此时对应的权系数就是在最小均方误差意义上的最优值[16]。
1.3SATDE算法
SATDE算法的基本思路如下: 采用式(1)的Sigmoid函数对采集的带噪声的信号进行非线性变换;然后,利用自适应滤波器对时间延迟这一参数的估计转化为对自适应滤波器参数的估计。图3所示的通用自适应滤波器在时间延迟估计的具体应用时,输入信号为两路传感器接收的信号x1(n)、x2(n),即
x(n)=x1(n),d(n)=x2(n)
通常,假定两接收信号x1(n)和x2(n)满足如下的离散信号模型:
(2)
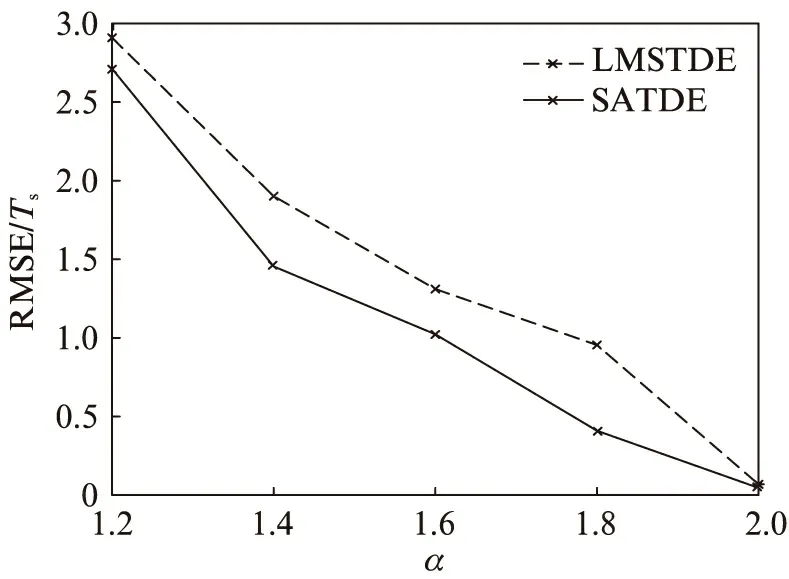
式中,s(n-d1)、s(n-d2)为两个接收传感器接收到的源信号;d1、d2分别为源信号到达两个接收传感器的时间延迟;λ为衰减因子(通常,取λ=1);v1(n)、v2(n)分别为两个接收传感器接收到的背景噪声,通常具有一定的脉冲性,可用SαS来描述。假设信号与噪声、噪声与噪声是独立统计的,需要估计的两路接收信号的相对时延差真值D=d2-d1,假设d1 自适应时间延迟估计方法将时间延迟估计问题转化为滤波器的参数估计问题,其原理结构如图4所示。 图4 自适应时间延时估计原理结构图Fig.4 Block diagram of adaptive timedelay estimation method 信道对两信号x1(n)、x2(n)的相对延迟可以用横向自适应滤波器(MA模型)来模拟: (3) 式中,w(i)(i=1~Q)为自适应滤波器加权系数;i为加权系数序号;Q为滤波器阶数;D为实际时延值,取Q>D。当i=D时,w(i)有最大值,即当i≠D时,|w(i)|<|w(D)|。 这样,对时间延迟的估计就转化为对横向滤波器权系数最大值位置的估计。本文利用自适应信号处理技术来估计时间延迟时,横向滤波器可以在最小均方误差准则控制下自适应地达到最优值。 现推导SATDE算法。基于最小均方误差准则算法的代价函数为 J(n)=E[|e(n)|2] (4) e(n)=x2(n)-y(n) (5) y(n)=xT(n)w(n)=wT(n)x(n) (6) 用最速下降法得到MA滤波器权矢量的迭代为 w(n+1)=w(n)+μe(n)x(n) (7) 式中,x(n)=[x(n)x(n-1) …x(n-M)]T为输入信号矢量;w(n)=[w0(n)w1(n) …wM(n)]T为权系数矢量;μ为自适应滤波器的收敛因子,常取一个较小的数。 本文通过计算机仿真实验,验证SATDE算法在高斯和非高斯SαS噪声条件下的估计性能,并与经典的基于最小均方时间延迟估计(Least Mean Square Time Delay Estimate, LMSTDE)算法进行比较。 图5 α =1.5、MSNR=0dB时,LMSTDE、SATDE算法时间延时估计的收敛曲线Fig.5 Convergence curves of time delay estimation for LMSTDE and SATDE with α=1.5 and MSNR=0dB (2) 当MSNR=0dB,α=1.2,1.4,1.6,1.8,2.0时,研究LMSTDE、SATDE算法对到达时间差的估计性能,即两算法估计的均方根误差(Root Mean Square Error, RMSE),如图6所示。由图可见,当MSNR=0dB,α<2时,SATDE算法估计的RMSE均小于LMSTDE算法;当α=2时,即噪声高斯条件下,两者估计的RMSE相当。实验表明,在信号噪声脉冲条件下,SATDE算法较LMSTDE算法对时间延迟估计的性能要好;在信号噪声高斯条件下,SATDE与LMSTDE算法对时间延迟估计的性能相当。由此可见,SATDE算法在高斯和非高斯脉冲噪声下均具有较好的估计性能。 图6 当MSNR=0dB,α不同时,LMSTDE和SATDE算法时延估计的RMSEFig.6 TDE RMSE of LMSTDE and SATDE algorithmswith MSNR=5dB and different α values (3) 当α=1.5,MSNR=-10~10dB时,研究LMSTDE、SATDE算法的估计性能,图7给出了α=1.5,MSNR=-10~10dB时,LMSTDE、SATDE时延估计结果的RMSE曲线。由图可见,当噪声脉冲特性相同、MSNR不同时,SATDE算法估计的RMSE均小于LMSTDE算法。实验表明,在信号噪声具有脉冲性的情况下,对于同一信噪比的信号,SATDE算法对时间延迟估计的性能比LMSTDE算法要好。 图7 当α=1.5,MSNR不同时,LMSTDE和SATDE算法时延估计的RMSEFig.7 TDE RMSE of LMSTDE and SATDE algorithmswith α=1.5 and different MSNRs 上述计算机数值仿真结果表明,LMSTDE算法较适用于在高斯噪声环境下的时间延迟估计,当信号噪声偏离高斯分布时,估计的精度降低,甚至不能得到可信的结果。而SATDE算法在高斯和非高斯脉冲噪声下均有较好的估计性能,尤其在非高斯脉冲噪声条件下,估计的精度明显优于LMSTDE算法,说明LMETDE算法是一种鲁棒性较强的时间延迟估计方法,比经典的LMSTDE算法有更宽的适用范围。 本文提出一种基于Sigmoid变换的自适应时间延迟估计算法(SATDE)。该算法先对信号噪声进行Sigmoid非线性变换,使其在抑制脉冲噪声的同时,较少地影响到信号本身,改善和提高了最小均方误差准则下的估计结果。 计算机数值仿真实验验证了SATDE算法在高斯和非高斯脉冲噪声条件下,均具有良好的估计性能,尤其在噪声不符合高斯分布的条件下,SATDE较LMSTDE算法具有更好的估计性能。因此,在信号噪声条件不符合高斯分布或未知分布的情况下,SATDE算法是一种较好的选择。 [1] 沈国清,安连锁,姜根山,等.电站锅炉声学测温中时间延迟估计的仿真研究.中国电机工程学报,2007,27(11): 57-61 [2] Jin Maolin,Kang S H,Chang P H.Robust compliant motion control of robot with nonlinear friction using time-delay estimation.IEEE Transactions on Industrial Electronics,2008,55(1): 258-269. [3] Kocak F,Celebi H,Gezici S,et al.Time-delay estimation in dispersed spectrum cognitive radio systems.Eurasip Journal on Advances in Signal Processing,2010: 115-119. [4] Sun Jian,Lin Weijun,Zhang Chengyu,et al.Time delay estimation in the ultrasonic flowmeter in the oil well.Physics Poocedia,2010,3(1): 781-788. [5] 刘文红,邱天爽,胡婷婷.一种韧性的高分辨率多径时延估计方法.系统工程与电子技术,2008,30(1): 41-45. [6] 盛虎.分数阶信号合成与滤波技术研究及应用.大连: 大连理工大学,2011: 50-85. [7] 邱天爽,唐洪,刘海龙.统计信号处理: 医学信号分析与处理.北京: 科学出版社,2012: 77-93. [8] Sadler B M,Liu Ning,Xu Zhengyuan.Ziv-zakai bounds on time delay estimation in unknown convolutive random channels.IEEE Transactions on Signal Processing,2010,58(5): 2729-2745. [9] Nikias C L,Shao Min.Signal processing with Alpha-stable distributions.New York: John Wiley & Sons Inc,1995: 5-35. [10] Wang Changcheng,Liao Mingsheng,Li Xiaofeng.Ship detection in SAR image based on the alpha-stable distribution.Sensors,2008(8): 4948-4960. [11] Salas-Gonzalez D,Kuruoglu E E,Ruiz D P.Modelling and assessing differential gene expression using the alphastabledistribution.International Journal of Biostatistics,2009,5(1): 235-251. [12] Ma X,Nikias C L.Joint estimation of time delay and frequency delay in impulsive noise using fractional lower order statistics.IEEE Transactions on Signal Processing,1996,44(11): 2669-2687. [13] 张雨浓,陈俊维,刘锦荣,等.基于权值与结构确定法的单极Sigmoid神经网络分类器.计算机应用,2013,33(3): 766-770,809. [14] 谭论正,夏利民,夏胜平.基于多级Sigmoid神经网络的城市交通场景理解.国防科技大学学报,2012,34(4): 132-137. [15] 王宏禹,邱天爽.自适应噪声抵消与时间延迟估计.大连: 大连理工大学出版社,1999: 1-7. [16] 刘文红,范光宇,赵莹,等.一种脉冲噪声下的鲁棒性自适应回波抵消方法.上海电机学院学报,2012,15(5): 290-294. Adaptive Time Delay Estimation Based on Nonlinear Transform LIUWenhong1a,LEIPeng1b,ZHANGShuai1b,GUODongmei2,QIUTianshuang3 (1. a. School of Electronic Information Engineering, b. School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China; 2. Department of Radiology, The Second Hospital of Dalian Medical University, Dalian 116027 Liaoning, China; 3. Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024 Liaoning, China) The actual signals obtained often contain impulse noise. This makes traditional algorithms inaccurate. In this paper, an adaptive time delay estimation algorithm is proposed based on the sigmoid transform (referred to as SATDE). Signals containing impulse noise are non-linearly transformed using the sigmoid function. An adaptive filter is then used to estimate parameters of the signal time delay. Numerical simulation results show that SATDE is suitable for signals with both Gaussian noise and impulse noise. It is concluded that SATDE is a robust time delay estimation algorithm. time delay estimation; adaptive filtering; impulse noise; nonlinear transformation; sigmoid function 2014 - 08 - 19 国家自然科学基金项目资助(61172108);上海市教育委员会科研创新项目资助(12YZ187);上海电机学院重点学科项目资助(10XKF01) 刘文红(1967-),女,教授,博士,主要研究方向为非高斯信号处理、时延估计技术, E-mail: liuwenhong@sdju.edu.cn 2095 - 0020(2014)05 -0254 - 05 TN 911.7 A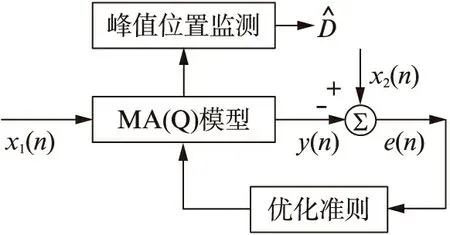
2 计算机数值仿真实验
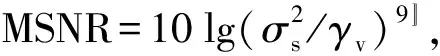



3 结 语
