含能子弹膛内抛射过程的数值模拟

叶耀野，杨云川，张 寅

(1.沈阳理工大学 装备工程学院，辽宁 沈阳 110159； 2.大连德堡钢格板有限公司 技术部，辽宁 大连 116450)

含能子弹膛内抛射过程的数值模拟

叶耀野1，杨云川1，张 寅2

(1.沈阳理工大学 装备工程学院，辽宁 沈阳 110159； 2.大连德堡钢格板有限公司 技术部，辽宁 大连 116450)

为研究子弹膛内抛射，以某新型结构防空榴弹战斗部为基础，建立含能子弹膛内抛射过程数值模拟数学模型，运用ANSYS/LS-DYNA软件模拟火药燃烧、推板及含能子弹在膛内的运动过程，得到各层含能子弹出膛时相对速度曲线，并将模拟结果与理论估算值进行比较。结果表明:模拟数据可为其结构设计和毁伤威力计算提供参考。

内弹道；数值模拟；含能子弹

在现代防空反导体系中，通常把对于来袭导弹的“近程”拦截作为最后一道“屏障”，并因此越来越受到各国的重视。为提高对来袭导弹的毁伤效应与拦截成功率，目前大多采用子母弹的形式将子弹从母弹中高速抛射出膛在空中形成“弹雨”，从而在与目标相遇区域形成较高的毁伤威力。

马光勇等[1]对破片战斗部的应用现状和定向战斗部如何反导等问题进行了研究，阐述了破片对目标的杀伤原理。何勇等[2]以巡航导弹为研究对象，运用ANSYS/LS-DYNA软件模拟打击过程并分析了各结构间的配合情况，得到了破片侵彻靶板时的相关数据。但目前关于子弹从母弹中抛射的过程大多采用传统理论计算，模拟仿真得到的数据较少。

本文采用ANSYS/LS-DYNA动力学软件，对某新型结构防空榴弹炮战斗部含能子弹膛内运动过程进行模拟，其子弹抛射采用气动力抛射方式。模拟结果可为实际加工中的结构设计、毁伤威力计算和所选火药性能的判定提供参考。

1 有限元模型的建立

1.1 物理模型

在有限元计算模型建模中含能子弹共分为五层，其中外层6个，里层6个,总计60个含能子弹并成轴对称排列。从演示清晰角度出发，演示时选取二分之一战斗部模型如图1所示。从提高运算速度角度出发，实际计算时选用四分之一战斗部模型[2]。单位制为cm-μs-g。

图1 战斗部整体结构示意图

计算模型直径为76mm，总长为165mm，装填子弹的壳体厚为13.5mm，底部长为105mm；含能子弹直径与高均为12mm；装药直径与高均为6mm；推板直径为47mm，高为10mm；挡板直径为56mm，高为2mm。含能子弹壳体、推板、挡板及战斗部壳体四种结构均采用45号钢，装药为铝粉与聚乙烯按体积比1∶4的混合物，火药采用2/1樟。

1.2 计算模型[3]

计算中对固态结构与火药分别采用Language与ALE算法。含能子弹壳体、推板、挡板及战斗部壳体的强度采用Johnson Cook方程描述，即

(1)

表1 材料性能参数

火药点火位置设在轴线中点处。未爆火药和已爆火药的状态方程均采用JWL方程，即

(2)

式中:P为压力；ν=V/V0为相对体积；e为初始比内能；A、B、R1、R2和ω均为JWL状态方程参数，取值见表2。

表2 子弹内部装药的JWL状态方程参数表

2 模拟结果及分析

含能子弹出膛的数值仿真模拟是一个火药燃烧推动推板、推板推动含能子弹出膛的连续运动过程。为方便观察含能子弹的膛内运动过程，在后处理中只显示战斗部壳体、推板及含能子弹三个部分，各层子弹出膛瞬间时的状态如图2～图6所示。

图2 第一层含能子弹出膛(100μs)

为进一步了解含能子弹出膛速度变化情况，分别选取最内层的含能子弹底部边缘单元体为研究对象，如图7所示。A、B、C、D、E五个单元速度曲线如图8所示。

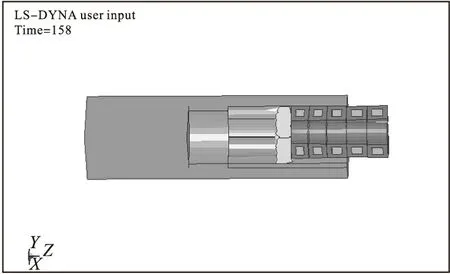
图3 第二层含能子弹出膛(158μs)

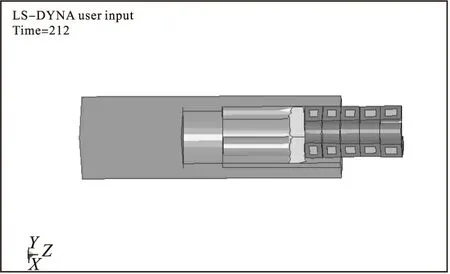
图4 第层含能子弹出膛(212μs)

图5 第四层含能子弹出膛(258μs)

图6 第五层含能子弹出膛(298μs)

由图8可知:(1)各单元初始运动时刻温度略有差异；(2)各层含能子弹在出膛过程中均出现速度小幅度下降现象，并在60μs左右取得相同值；(3)此后各单元体速度略有上升，并逐渐趋于稳定，在298μs最后一层子弹出膛。

图7 含能子弹速度取点示意图

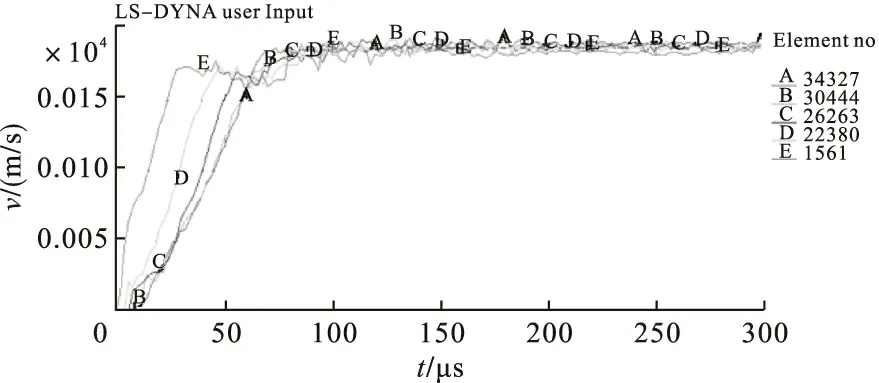
图8 含能子弹速度曲线图

3 出膛速度的理论计算及比较

含能子弹膛内运动过程复杂，涉及火药燃烧推动推板及子弹做功、火药自身损耗及摩擦阻力等。采用传统的火药内弹道抛射过程原理进行理论估算。

3.1 战斗部各结构质量及其参数[4]

含能子弹总质量为577.3g；单个质量为9.6g；挡板质量为38.7g；火药质量为69.4g；推板质量为156.9g；战斗部壳体质量为3853.9g；战斗部抛射内腔的横断面积为S=0.199dm2；最底层子弹运动全程Lg=0.600dm；抛射药室容积W0=0.163dm3。

3.2 药形系数取值及内弹道计算[4]

χ=1.09;λ=-0.08;χλ=-0.09；φ=1.25；f=80×104kg·dm/kg

χ、λ和χλ均为火药形状特征量；φ为次要功计算系数；f为火药力。膛内常量计算为

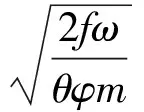
式中:ω为装药药量；α为火药气体余容；θ为计算参数，取值为0.2；m为抛射质量；l1为药室自由容积扩径度；VK为膛内最大抛射速度；lk为抛射最大长度。将以上参量代入公式(3)得含能子弹出膛时的相对速度为

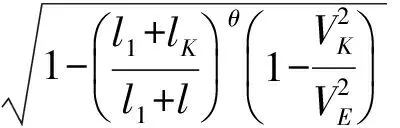
(3)

3.3 含能子弹平均绝对速度估算及比较

为与模拟结果进行比较，采用简化力学模型，忽略抛射药在膛口附近对子弹速度的影响，忽略子弹出膛瞬时相互之间的耦合作用，对含能子弹平均绝对速度进行估算，在含能子弹出膛瞬时应用动量守恒定理得

m1V1=m2V2

(4)

对因火药做功而附加的能量应用能量守恒定理得

(5)

式中：m1为战斗部壳体总质量；V1为战斗部壳体绝对速度；m2为含能子弹总质量；V2为含能子弹绝对速度，Vr为含能子弹相对速度。由此得

含能子弹出膛平均绝对速度的数值模拟和理论估算分别为190.0m/s和177.6m/s，相对误差为6.63%。

4 结论

(1)模拟结果表明，各层含能子弹出膛的相对速度值相差较小，第一层含能子弹速度最大，然后依次递减。含能子弹在膛内的速度变化有先后，初期最底层的速度与其他层差异大。各层子弹在约60μs时刻，速度均出现小幅度下降，而后回升并逐渐趋于一个稳定值。

(2)理论计算与模拟结果的比较证明该仿真模型合理。模拟所得的相关数据符合实际情况，研究结果可为子母弹结构设计、火药装填量、出膛速度判定和毁伤威力计算提供参考，并为不同初始条件的模拟提供理论数据。

[1]马光勇，罗兴柏，张玉令.国内破片速度测试技术研究近况及发展趋势[J].四川兵工学报,2009,30(9):125-127.

[2]何勇，刘源君.预制破片战斗部对巡航导弹毁伤仿真研究[J].弹箭与制导学报,2005,25(1):45-51.

[3]李裕春，时党勇.ANSYS10.0/LS-DYNA基础理论与工程实践[M].北京：中国水利水电出版社，2006.

[4]姚红，吴玉斌，林常海.125mm轴线场分爆式弹药抛射内弹道特性分析[J].沈阳理工大学学报，2007,26(4)：59-61.

TheNumericalSimulationofProcessThatTheBulletisMassEjection

YE Yaoye1,YANG Yunchuan1,ZHANG Yin2

(1.Shenyang Ligong University,Shenyang 110159,China； 2.Dalian AW Gratings LTD,Dalian 116450，China)

In order to study the processes of projecting bullet in bore,the numerical simulation model of the projecting energetic bullet in bore is established in this paper,based on a new structure of antiaircraft shrapnel warhead.The processes of the gunpowder combustion,pushing board and energy bullet's movement in bore are simulated,using ANSYS/LS-DYNA software.The relative velocity curves of the energetic bullets in each layer can be obtained.The simulation results are compared with theoretical estimates.The simulation results can provide a reference for the structure design and damage power calculation.

internal ballistic;numerical simulation;energy bullet

2014-01-13

叶耀野(1986—)，男，硕士研究生；通讯作者：杨云川(1961—)，男，教授，研究方向：颗粒材料冲击破碎数值模拟.

1003-1251(2014)05-0073-04

TJ391

A

赵丽琴)