三维激光测距系统设计与标定方法研究

谷晓杰，卜春光，陈 成，周浚哲

(1.沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159； 2.中国科学院沈阳自动化研究所，辽宁 沈阳 110016 )

三维激光测距系统设计与标定方法研究

谷晓杰1，2，卜春光2，陈 成2，周浚哲1

(1.沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159； 2.中国科学院沈阳自动化研究所，辽宁 沈阳 110016 )

针对传统三维激光测距系统标定结果精度低的缺陷，设计一套由云台和激光测距装置组成的三维激光测距系统。提出了采用平面特征的标定方法。在初始标定值下，对一个已知平面三维扫描后的若干帧，每帧的若干点作为试验点，用Matlab做非线性优化，来找到一个合适的标定值，使得试验点拟合后得到的平面到真实平面的距离平方和最小。该标定方法简单，经过试验证明，此方法能精确地实现激光的标定。

激光标定；平面拟合；三维激光测距系统；机器人

近年来，随着科学技术的发展，激光测距仪被越来越多地应用于航空航天[1]、机器人[2]等领域。常见的激光测距仪仅能获取二维的平面数据，为了获取三维环境信息,通常需要构建三维激光测距系统。常见的三维激光测距系统按照其机械结构可以分为通过旋转激光镜面获取三维测距信息以及通过选择激光测距仪本体获取三维测距信息两类。旋转镜面的三维激光测距系统对机械加工精度要求较高，难以设计实现。市面上已有的旋转镜面激光测距系统，如Velodyne Lidar系统，成本较高。本文采用将激光测距仪与云台固连构建三维激光测距系统。为了获取精确的三维测距信息，需要对三维激光测距系统进行标定。三维激光测距系统的标定主要对激光测距仪相对于基准坐标系的相对位姿进行标定。待标定的相对位姿包括激光测距仪坐标系相对于基准坐标系的三个姿态角(包括偏航角α，俯仰β角，横滚γ角)以及三个坐标轴偏移量(包括x轴，y轴以及z轴偏移量)。这六个待标定参数记为S=(α,β,γ,xL,yL,zL)，三维激光测距仪标定即为通过标定算法解算得到这六个参数的最优估计值，通常三维激光测距系统的标定方法大都采用标准模板法[3]，即通过标准模板上三维坐标已知的被测点将传感器坐标系和测量基准坐标系联系起来，进而求得两个坐标系间的变换方程。然而，由于扫描测距系统的激光脉冲是不可见的、而且扫描点是离散的，因此被测点在基准坐标系内的三维坐标无法精确获得。为此本文提出了一种新的激光标定方法，即在初始标定值S0下，以扫描后的若干帧，每帧的若干点作为试验的空间点(这些点是对真实环境中的平面的扫描点)，通过非线性优化算法来找到一个合适的标定值S，使得试验空间点经扫描后得到的点到相应的空间拟合平面的距离平方和为最小。

1 三维激光测距系统

1.1 系统硬件简介

本文针对由云台和激光组成的三维激光测距系统设计控制系统，三维激光测距系统试验平台如图1所示，它由两自由度的云台PTU-D47(包括偏转单元和俯仰单元两部分)和激光UTM-30LX组成。

二维激光测距仪UTM-30LX由HOKUYO公司生产，测距最远为30m,扫描范围为270°，DC12V输入，25ms扫描时间。云台装置PTU-D47有两个自由度，其中俯仰单元转动范围+/-159°，偏转单元转动位置范围为-47°～+31°，俯仰单元最大转速为300°/s,偏转单元最大转速为60°/s,DC12V输入，内部有集成的控制器。通过控制云台俯仰，二维激光测距仪扫描空间不同平面的环境信息，从而可实现三维扫描功能。PC机通过COM口与激光通讯。串口参数为：波特率115200b/s、8位数据位、1位停止位、无校验位。PC机通过RS232串口与云台进行通讯，串口参数为：波特率9600b/s、8位数据位、1位停止位、无校验位。

图1 三维激光测距系统

1.2 系统软件设计与实现

利用PC机开发基于Qt的应用程序，首先初始化激光和云台，若两者之一初始化失败则程序退出，如果成功，则GUI界面显示云台的基本信息(如云台最大最小速度，运动的极限范围等)。然后用户可以设定云台步进大小，随后开启云台线程，云台每进一步，激光就采集一帧数据(步进模式保证测量的数据尽可能准确)。并结合当前的云台姿态经过坐标转换来计算出基于基准坐标系下的激光数据的三维表示，将其载入到点云中，用QVTKWidget控件进行显示。然后云台继续步进，如此反复，直到云台达到极限位置，对点云进行清空，然后云台继续步进，重复上述步骤，就实现了环境的实时三维重建[4]。

2 三维重建方法

由于二维激光测距仪仅能获取二维的测距信息，为了获取全局一致的三维环境信息，需要将激光测距信息与云台位置信息融合。

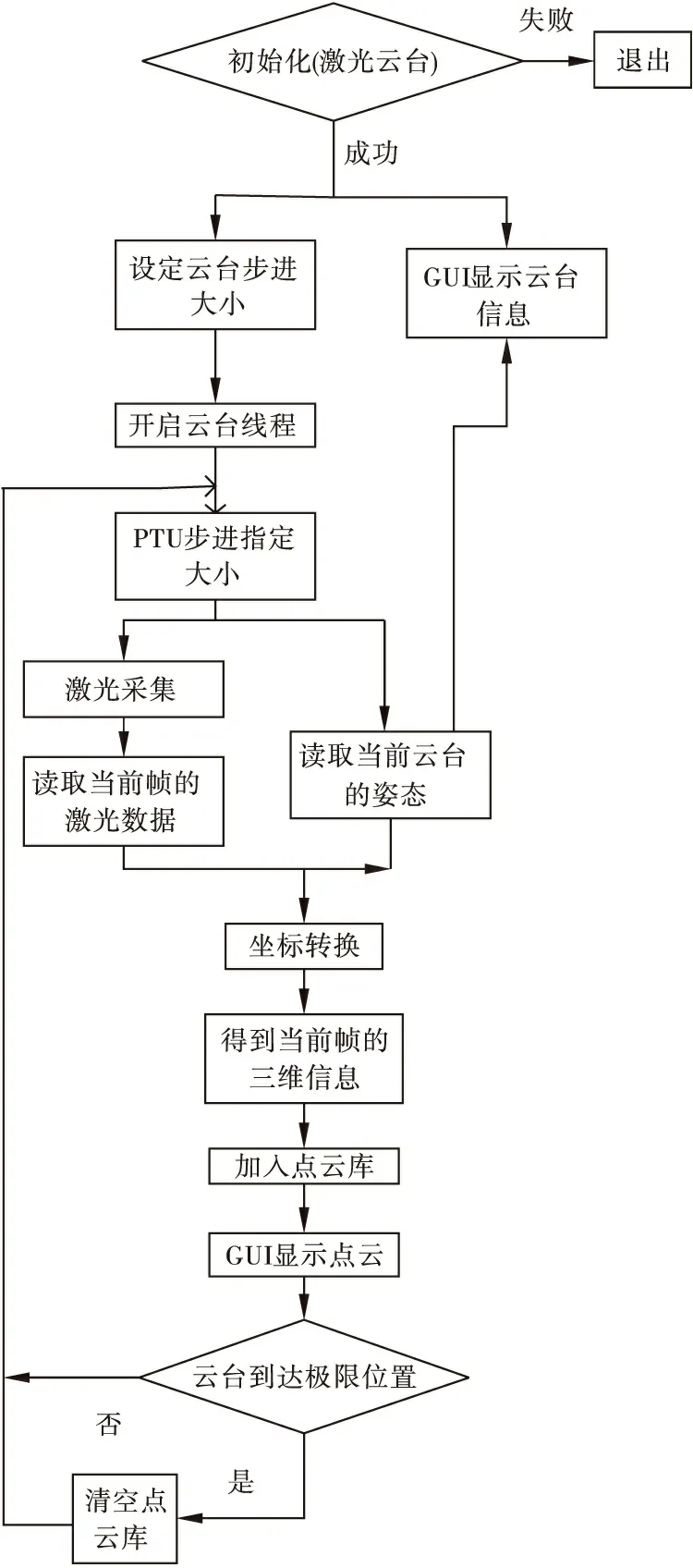
图2 系统软件设计

2.1 坐标系统

该系统中的坐标系包括：{R}参考坐标系，该坐标系与云台基座固连，为固定的坐标系；{T}俯仰坐标系，该坐标系与云台俯仰轴和偏转轴交点固连，由于云台俯仰运动，该坐标系与{R}坐标系的俯仰角为时变的(该俯仰角可以通过读取云台的俯仰角精确获取)；{L}激光测距仪坐标系，该坐标系与俯仰摆臂固连，坐标系原点为激光测距仪光源光心。三个坐标系都为右手坐标系，x轴指向正前方、y轴指向左侧、z轴指向上方。如图1中给出了{T}坐标系和{L}坐标系。

激光测距仪获取的二维测距信息包括若干个量测点，每个量测点由该点P至激光测距仪光心的距离ρ以及该量测点的角度θ构成，即P=(ρ,θ)。该量测点在{L}下的三维坐标为：PL=[ρcosθρsinθ]T。那么，激光测距点三维重建即为将PL通过旋转平移转换到{R}坐标系下，构建一致的环境模型。

2.2 三维重建过程

设{L}相对于{T}的偏转角为α、俯仰角为β、横滚角为γ。偏移量分别为xL、yL、zL。那么，将PL转换至{T}的过程可以用以下公式描述：

PT=RZ(α)RY(β)RX(γ)PL+TPLORG

(1)

式中:TPLORG=[xLyLzL]T;RZ、RY、RX分别为绕z、y、x的旋转矩阵。

为简化运算，将{R}坐标系原点设定与{T}坐标系原点重合，{R}坐标轴与{T}在俯仰角为0时坐标轴重合。{T}坐标系相对于{R}坐标系仅有俯仰角度变化。那么，将{T}下的坐标点PT转换至{R}坐标系的过程可以用如下公式描述：

PR=PZ(τ)PT

(2)

式中τ为云台的俯仰角，可以通过读取云台编码器实时在线获取。

总结以上转换过程，由激光测距仪量测点P=(ρ,θ)获取其在参考坐标系下的坐标可以用以下公式描述：

PR=RZ(τ)(RZ(α)RY(β)RX(γ)PL+TPLORG)=

(3)

式中：ρ、θ分别为P点距离光心距离及对应角度，由激光测距仪获取其量测值；τ为云台俯仰角，可以通过读取云台编码器获取；α、β、γ、xL、yL、zL为激光测距仪相对于{T}坐标系的安装位姿。为了获取精确的环境模型，需要通过标定得到这6个未知变量。

3 三维激光测距系统标定

3.1 三维激光测距系统标定方法

为了获取精确的环境模型，需要对激光测距仪相对于俯仰坐标系的位姿参数S=(α,β,γ,xL,yL，zL)进行标定。

常规的三维激光测距系统标定方法与摄像头标定方法类似，即采用标定模板通过构建真实环境与三维测距系统的测距点的对应关系，再通过求解转换矩阵得到三维激光测距系统的待标定参数。由于三维激光测距系统的量测点是稀疏的，难以精确构建真实环境与量测环境的对应关系，最终导致标定结果不够精确。针对这一问题，本文提出了基于平面特征的标定方法。

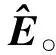
(4)

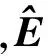
本文采用最小二乘法求解平面，设平面上的N个点分别为{(x1,y1,z1),…,(xN,yN,zN)}，平面方程为

axi+byi+c=zi

(5)

式中a、b、c为平面的参数。采用最小二乘法拟合平面[5]来求解该平面参数：

(6)

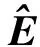
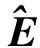
(7)

激光测距仪安装位姿的标定过程即为调整待标定参数使得该偏差代价值最小。本文采用非线性优化[6]方法求解待标定参数。

该标定过程包括以下几个步骤：

(1)运行三维测距系统采集原始的传感器数据，包括云台俯仰角，激光量测点；

(2)测量得到待标定参数初始估计值；

(3)采用公式(3)及当前标定参数估计值将传感器量测点转换到参考坐标系下；

(4)采用公式(6)求解平面的参数；

(5)采用公式(7)求解真实平面与量测平面的偏差代价值，若偏差代价值以及参数满足要求则停止迭代，否则继续步骤(6)；

(6)采用非线性优化方法对待标定参数进行调整，得到新的标定参数，跳转至步骤(3)。

3.2 三维激光测距系统标定实验

为了对三维激光测距系统进行标定，本文选择室内的实验场景进行传感器数据采集。初始的待标定参数为S0=(0.0,0.0,0.0,0.0,0.1,0.05)，由游标卡尺测量可得，其中角度单位为弧度，距离单位为米。由初始参数得到的三维环境的点云数据如图3所示。

图3 初始参数解算得到的三维环境点云图

由于该场景包括各种环境特征，为了方便标定，首先手动从中选取出一个平面上的点云量测点，再基于这些平面点进行标定实验。本文选择的平面点云为第5-160帧激光测距仪量测帧中的第361-801个量测点，如图4所示。

本文的标定过程在CPU为Intel Core 2 Duo CPU E7500 2.93GHz，内存为2.0GB的台式计算机上基于Matlab实现，采用Matlab的非线性优化函数进行参数求解，其迭代过程如图5和图6所示。

图4 平面点云数据

在非线性优化的过程中，待标定参数不断调整，其(包括偏转角、俯仰角、横滚角、x轴向距离、y轴向距离、z轴向距离)调整过程如图5所示。偏差值，即平面上点到拟合平面距离平方和的变化过程如图6所示。考虑到通过游标卡尺量测得到的初始参数(即标定参数既要使偏差值尽量小又要接近于初始参数)，最终三维测距系统的标定结果为

S=(0.0026,0.0,0.0017,0.003,0.1,0.0463)

即，激光测距仪相对于俯仰坐标系安装的偏转角为0.0026弧度，俯仰角为0.0弧度，横滚角为0.0017弧度，x轴向距离为0.003米，y轴向距离为0.1米，z轴向距离为0.0463米。该组参数使得偏差代价值由最初的0.7573减小到0.7404，考虑到激光测距仪及云台的量测误差，该结果较为合理。

图5 待标定参数调整过程

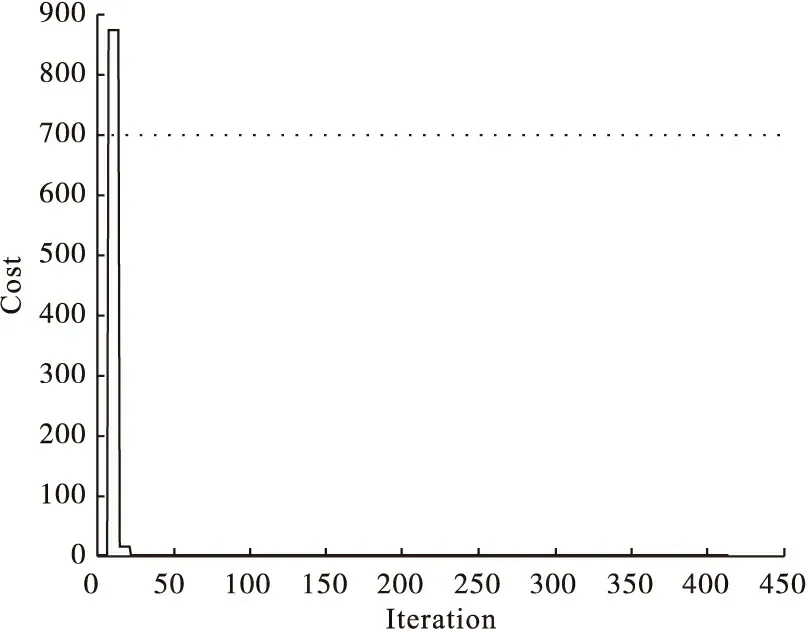
图6 偏差代价值变化过程

为了验证该标定结果，本文采集了多组平面环境的数据，多次重复进行标定实验，并将该标定结果带入进行验证。标定前后拟合平面的距离平方和如表1所示。

由于受论文篇幅限制，该表仅列出了实验中的8个平面的初始代价值以及标定后的代价值。不同平面的代价值的差异是由平面大小以及距离激光测距仪的距离不同导致的。从表1中可以发现，标定得到的参数能够有效的减小该代价值，尽

可能得到真实的平面。因此，该标定结果可以有效地提高三维激光测距系统的测量精度。

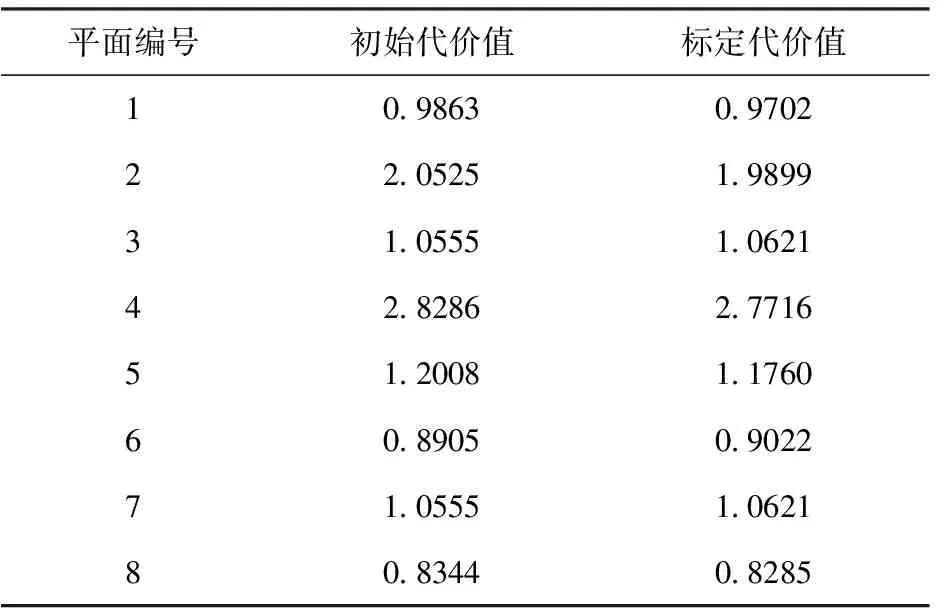
表1 多组平面标定前后代价值对比

4 结束语

针对由二维激光测距系统和云台组成的三维激光测距系统，介绍了其硬件组成、软件设计与实现、三维重建方法，重点研究了基于平面特征的标定方法。经实验证明，标定得到的参数能够有效减小代价值，该标定方法能较为精确地实现扫描系统的标定。

[1]武汉华工激光工程有限责任公司.激光技术在航空航天领域的应用[J].光电产品与资讯,2012，3(5)：27-28.

[2]杨洗陈.激光加工机器人技术及工业应用[J].中国激光，2009,36(11)：2780-2798.

[3]余祖俊，杨娅楠，朱力强.三维激光扫描测量系统标定方法研究[J].电子测量与仪器学报，2007，21(6)：31-35.

[4]项志宇，李斌.基于2D激光雷达的快速3D测距系统的设计与实现[J].传感技术学报，2006,19(6)：2638-2642.

[5]刘志平，石林英.最小二乘法原理及其Matlab实现[J]．中国西部科技，2008，17(7)：33-34.

[6]南倩，张秦艳，李金泉,等.工业机器人的局部标定[J].现代电子技术，2012，2(35)：81-83.

Design,ImplementationandCalibrationof3-DLIDARScanningSystem

GU Xiaojie1，2,BU Chunguang2,CHEN Cheng2,ZHOU Junzhe1

(1.Shenyang Ligong University,Shenyang 110159,China;2.Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang City,Shenyang 110016,China)

3D lidar scanning system has been widely used and calibration usually adopts standard template method,namely,sensor coordinate can be connected with the reference coordinate according to the known three-dimensional coordinates of the measured points,but low accuracy is its drawback.With regard to a 3D lidar scanning system composed of pan-tilt and lidar,the system components,software design and implementation as well as 3D reconstruction methods are introduced,which focus on the calibration based on plane.The method is to choose a number of points from a plane as the test points to give an initial calibration value,and it aims at finding a suitable calibration value，which makes sure that the distance from true plane to the fitting plane is shortest according to nonlinear optimization based on Matlab simulation.The calibration method is simple，which proves to be able to achieve precise calibration of the 3D lidar scanning systemt.

lidar calibration;plane-fitting;three-dimensional scanning system;robot

2013-11-11

国家863资助项目(2011AA040202)

谷晓杰(1987—)，女，硕士研究生；通讯作者：卜春光(1971—)，男，副研究员，研究方向：自主移动机器人控制与系统.

1003-1251(2014)05-0010-05

TP391

A

马金发)