求解线性椭圆型优化控制问题的多重网格方法

邱 岳 东

(暨南大学 信息科学技术学院，广州 510632)

有限差分法是计算机数值模拟最早采用的方法，该方法将求解域划分为差分网格，用有限个网格节点代替连续的求解域．有限差分法主要包括三个过程，即网格生成、有限差分离散方程的形成以及离散方程的求解．其中，有限差分离散方程的求解能够影响到数值计算结果的精确性和数值计算时间的高效性[1-2]．

我们通常可以通过加密网格来提高计算精度．但是，有限差分法迭代计算的收敛速度随着计算网格的增加而越来越慢[3-4]，计算精度无法继续提高，因此，我们需要寻找一种高效的求解方法．

多重网格法是求解大规模科学计算问题的有效方法，其基本原理在于一定的网格最容易消除与网格步长相对应的误差分量，对于离散方程，它在细网格上利用通常的迭代法消去残量的高频部分，然后把低频部分转移到粗网格上进行校正，经过若干次循环以后，获得满足精度的解[5]．该算法主要包括以下几个部分：网格剖分、网格粗化方法、模型问题的离散格式、松弛方法、限制与延拓以及迭代技术等．

本文利用集体平滑多重网格方法和多重网格最优化方法求解线性椭圆型优化控制问题，研究分析了多重网格法的网格剖分稀疏程度和最大循环次数对计算速度及精度的影响．文献[6]通过局部傅里叶分析证明了集体平滑多重网格方法的收敛性，而文献[7]则利用了利普希茨连续性证明了多重网格最优化方法的收敛性．此外，数值试验说明，这两种方法的收敛因子和迭代步数不随网格步长变化而增加，并且，集体平滑多重网格方法比多重网格最优化方法的收敛速度更快和更好的稳定性．

1 模型问题

1.1 优化控制问题的模型

优化控制是指在给定的约束条件下，寻求一个控制系统，使给定的被控系统性能指标取得最大值或最小值的控制．为了求解线性椭圆型优化控制问题，我们选取如下目标泛函：

(1)

其中:Ω为R2上的一个凸集，v>0为控制目标泛函的权重，z∈L2(Ω)是目标函数，而u是在Ω上的控制变量的分布函数．

此外，我们选取的目标泛函还需满足一定的偏微分方程约束优化条件，因此，在凸集Ω上的线性椭圆型优化控制问题的模型可以表示为：

minu∈UH(y,u),

-Δy-u=f,y|∂Ω=0

-Δp+y=z,p|∂Ω=0

vu-p=0.

(2)

其中:f∈L2(Ω)和U=L2(Ω)，p为拉格朗日算子．

1.2 优化控制问题的离散形式

本文考虑线性椭圆型控制问题偏微分方程约束条件基于有限差分法的离散化形式．首先，用Ωk来表示区域Ω离散化的参数形式，网格大小为hk(k=1,2,…L)，令hk-1=2hk，内部网格点的数目为nk，任意函数在区域Ωk里进行离散化之后，都可用一个nk维的向量表示．

那么，偏微分方程约束条件的离散形式如下：

-Δkyk-uk=fk,

-Δkpk+yk=zk,

vuk-pk=0.

(3)

这里，-Δk表示负五点拉普拉斯算子，x∈Ωk且x=(ihk,jhk)，i,j是网格点的按字典序的下标指数．因此，我们由Taylor展式可得

(4)

其中:在变量yi,j和pi,j的更新过程中，假定Ai,j、Bi,j的值为常量，并且可得

Ai,j=-(yi-1,j+yi+1,j+yi,j-1+yi,j+1)-h2fi,j,

Bi,j=-(pi-1,j+pi+1,j+pi,j-1+pi,j+1)-h2zi,j

(5)

将式(4)经过化简变形，并且定义yi,j=yi,j(ui,j),pi,j=pi,j(ui,j)，可以得到关于ui,j的四次多项式方程，并且根据Cardano-Tartaglia公式求得四次多项式方程的最小实数值：

(6)

该四次多项式方程的最小实数根即为椭圆型优化控制问题目标泛函的有限差分离散化问题的解，有了这一条件，我们可以得到一个完整且有效的平滑迭代．

2 集体平滑多重网格方法和多重网格最优化方法

集体平滑多重网格方法是基于一种应用到具有集体平滑性质的非线性多重网格全近似存储方法，主要是通过解决相配的偏微分方程在处理约束条件中的优化变量来解决优化控制问题，而且这种方法需要对问题进行集体平滑处理与内部网格算子转移．文献[8-9]都较详细地介绍了集体平滑多重网格方法在求解状态和控制约束条件下线性优化控制问题的应用．

Nash[10]和Lewis[11]首次将多重网格最优化方法应用到约束优化控制问题的求解．在应用多重网格最优化方法求解控制问题过程中，我们假设其外循环的控制函数为惟一独立的变量，而内循环则由一个单重网格和其他多重网格法构成的，而且，多重网格最优化方法具有更简易、更广泛的应用性[12]．

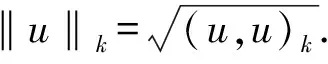
2.1 集体平滑多重网格方法的结构

为了阐明集体平滑多重网格方法，我们首先考虑如下方程组

Ak(ωk)=fk,

(7)

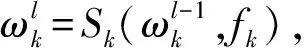
前光滑：

(8)

粗网格问题：

1) 计算细网格亏损量：

4)亏损量校正(由细网格到粗网格)

(9)

对粗网格问题Ak-1(ωk-1)=fk-1应用集体平滑算法进行r次循环(r=r1+r2)求得wk-1．

粗网格校正：

后光滑：

在Ωk上再对方程Ak(ωk)=fk应用γ2次平滑算法迭代，得到

其中:rk为残差因子，ωk-1表示一个相对于ωk的粗网格估计，同时，Ak-1(·)表示相对于Ak(·)较粗网格的散方程组，而且τk-1表示由细网格到粗网格的残差校正．

2.2 多重网格最优化方法的结构

为了能够更好地了解多重网格最优化方法，我们考虑一个局部离散的凸规划问题

(10)

而求解这个凸规划问题就等同于求解

▽Hk(uk)=fk．

(11)

其中:Hk(·)表示目标泛函，那么，在优化控制问题上，为了计算Hk(·)在uk的值，我们应计算yk(uk)的值，并且，还需要yk(uk)、pk(uk)来求解梯度函数▽Hk(·)的值．假设Sk为在向量空间Vk上的一个优化迭代算法，使得

成立．那么，多重网格最优化方法的结构为：

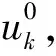
前光滑：

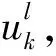
(12)

粗网格问题：

2)计算由细网格到粗网格的梯度校正，

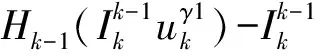
(13)

对粗网格最小化问题应用MGOPT算法的一次循环，

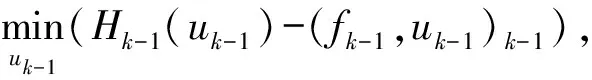
粗网格到细网格的最小化：

2)在方向e上进行一次线性查找来求得步长的值αk；

后光滑：

在Ωk上再对方程▽Hk(uk)=fk应用γ2次平滑算法迭代，得到

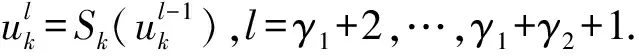
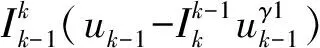
3 数值试验与分析

为验证集体平滑多重网格方法和多重网格最优化方法的收敛速度及其稳定性，给出了如下数值算例．见图1、2.

算例 测试函数f(x,y)，选择目标函数z，使其满足模型问题：

-Δy-u=f,

y|∂Ω=0.

假设Ω=(0,1)×(0,1)和f,z∈L2(Ω)，

f(x,y)=sin(x2+y2),

z(x,y)=

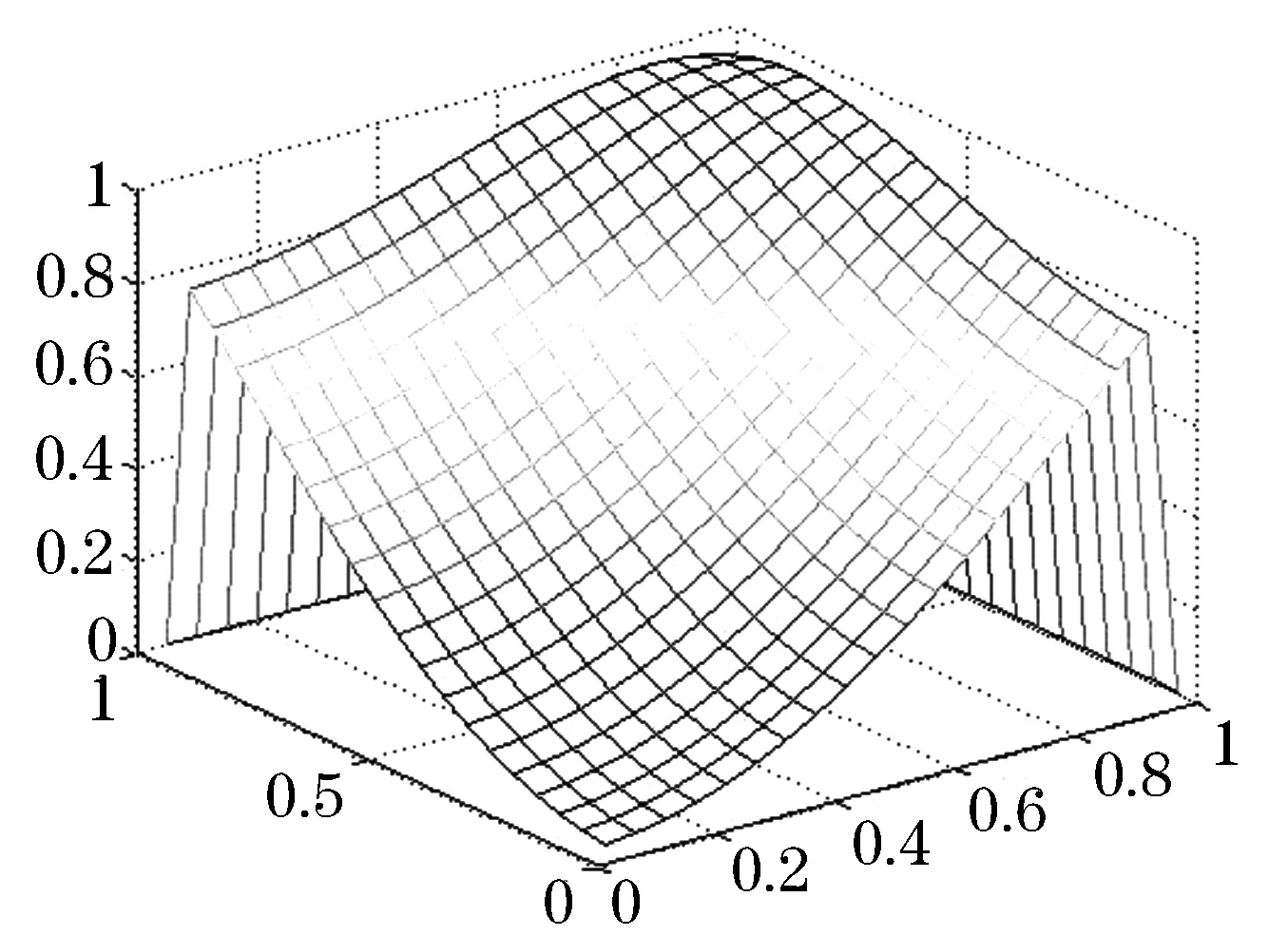
图1 测试函数f(x,y)

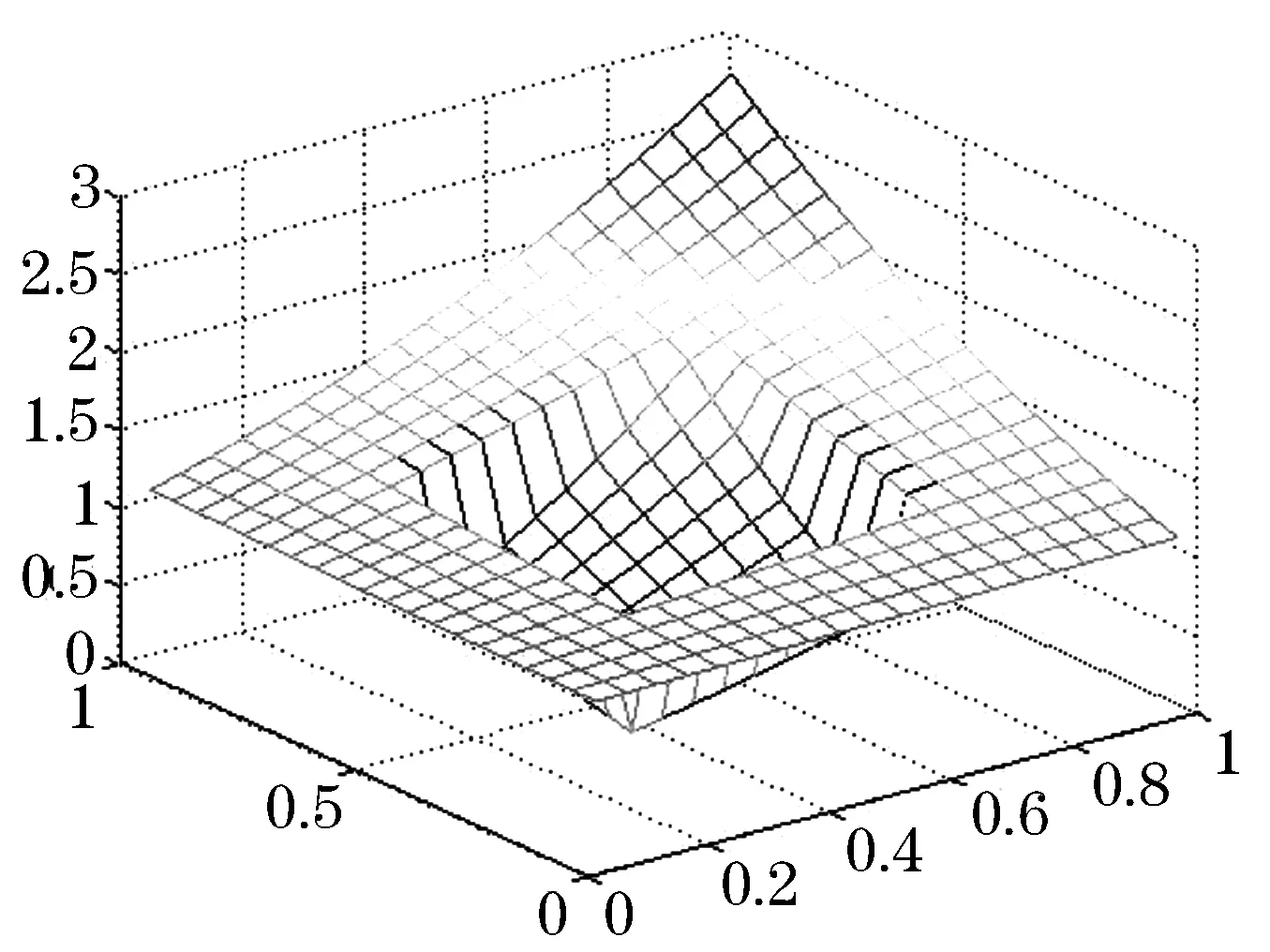
图2 目标函数 z

数值试验中，前光滑次数和后光滑次数统一选择为2次，即γ1=γ2=2，以Gauss-Seidel迭代法作为光滑算子，M为细层网格剖分数．取迭代终止条件为：tol=10-8，Iter为集体平滑多重网格方法的迭代次数，γ次迭代后，集体平滑多重网格方法的收敛因子记为

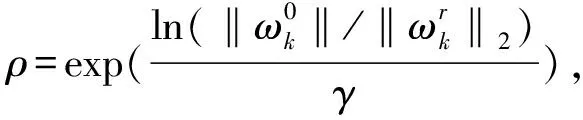
线性椭圆型的控制问题的数值试验结果可由表1，2给出．

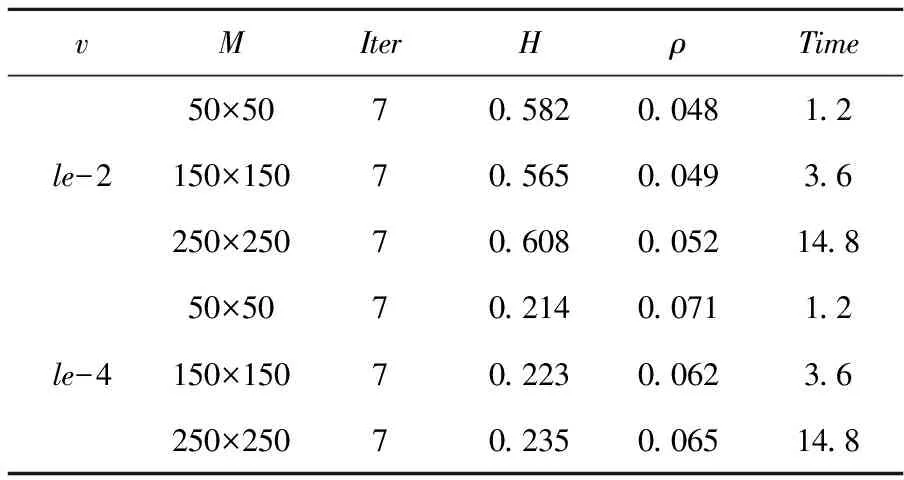
表1 利用集体平滑方法求解得到的数值结果

根据表1中的数据，时间单位为s，可以总结出以下的结论：

1)在多重网格循环次数相同的前提下，多重网格剖分的数目对运行的时间的影响相对较大，即影响运行时间的主要因素是求解区域剖分疏密程度，网格剖分越密，运行的时间越长；

2) 当参数取不同的值时，集体平滑多重网格方法都是在经过7次迭代之内收敛的；

3)集体平滑多重网格方法的迭代次数跟参数的取值和网格的疏密程度是互不影响的；

4)在相同的网格疏密程度的前提下，集体平滑多重网格的循环次数对运行时间的影响相对较小，即增大多重网格的循环次数时，运行的时间并没有大幅度变化，而是在一个很小的范围内浮动．

其中GM是梯度法，MGM是梯度格式的多重网格最优化方法，NCG表示非线性共轭梯度法，MNCG表示非线性共轭梯度格式的多重网格最优化方法，表2表示利用以上几种求解线性椭圆优化控制问题所耗用的CPU的时间，时间单位为s．

对于单重网格最优化方法，可利用梯度法和非线性共轭梯度法来进行求解，并且，根据表2中的数据，我们可以得到以下的结论：

1)当参数v的取值减小时，在对应相同的网格疏密程度的前提下，梯度法和梯度格式的多重网格最优化方法运行所需的时间是随着网格规模的增加而增加，并且，同时使用非线性共轭梯度法和非线性共轭梯度格式的多重网格最优化算法也具有这一特性；

2)当参数v的值确定时，相对应的网格剖分的疏密程度不相同，使用非线性共轭梯度格式的多重网格最优化算法都比使用梯度格式的多重网格最优化算法的收敛速度要快；

3)在表2中的这几种情形，多重网格最优化方法都极大地提高了单重网格最优化格式的独立性，并且根据表1相应的数据结果，多重网格最优化方法在网格剖分的疏密程度、收敛速度等因素上，跟集体平滑多重网格方法的数据结果有一定的可比性．

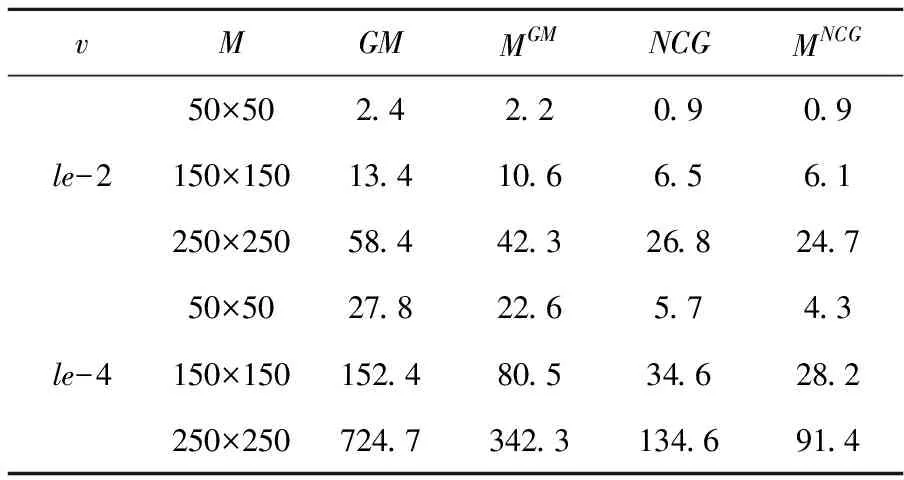
表2 利用多重网格最优化方法得到的数值结果

4 结 语

本文主要探讨了求解线性椭圆型优化控制问题的两种多重网格法：集体平滑多重网格方法和多重网格最优化方法．由数值试验结果表明，相对于多重网格最优化方法，集体平滑多重网格方法的求解速度更快和具有更好的稳定性，同时，这两种方法都说明了网格疏密程度的独立性和参数收敛的独立性，此外，对于单重网格优化问题，应用最优化问题多重网格方法可得到更为准确的数值结果；应用集体平滑多重网格方法，则需要对问题设计一个具体的集体平滑格式，再根据相应的迭代法进行运算，而最优化问题多重网格方法则只需要利用相应的迭代法进行操作．

参考文献：

[1] BORZ`1 A. Multigrid methods for parabolic distributed optimal control problems [J]. J Comput Appl Math , 2003, 157 (2): 365-382.

[2] BORZ`1 A. A multigrid scheme for elliptic constrained optimal control problems [J]. Comput Optim Appl, 2005, 31(3): 309-333.

[3] NOCEDAL J, WRIGHT S J. Numerical optimization [M]. New York: Springe, 1999.

[4] BORZ`1 A. High-order discretization andmultigrid solution of elliptic nonlinear constrained optimal control problems [J]. J Comput Appl Math, 2007, 200(1): 67-85.

[5] BORZ`1 A, KUNISCH K, KWAK D. Accuracy and convergence properties of the finite difference multigrid solution of an optimal control optimality system [J]. SIAM J Control Optim, 2003, 41(5): 1477-1497.

[6] BORZ`1 A. On the convergence of the MG/OPT method [J]. PAMM, 2005, 5(1): 735-736.

[7] OH S, BOUMAN C,WEBB K. Multigrid tomographic inversion with variable resolution data and image spaces [J]. IEEE Trans Image Proc, 2006, 15(9): 2805-2819.

[8] OH S, MILSTEIN A, BOUMAN C,etal. A general framework for nonlinearmultigrid inversion [J]. IEEE Trans Image Proc, 2005. 14(1): 125-140.

[9] LEWIS R M, NASH S G. A multigrid approach to the optimization of systems governed by differential equations [C]//Long Beach: Symposium on Multidisciplinary Analysis and Optimization, CA, 2000.

[10] LEWIS R M, NASH, S G. Model problems for the multigrid optimization of systems governed by differential equations [J]. SIAM J Sci Comput, 2005, 26(6): 1811-1837.

[11] NASH S G. A multigrid approach to discretized optimization problems [J]. Optim Methods Softw, 2000, 14(2): 99-116.

[12] OH S, MILSTEIN A, BOUMAN C,etal. Multigrid algorithms for optimization and inverse problems [J]. IEEE Trans Image Proc, 2005, 14(2): 125-140.