铝合金薄板结构多模态随机振动疲劳分析
2014-09-14陈欢欢谭韶毅谢慈航
陈欢欢,薛 璞,谭韶毅,谢慈航
(西北工业大学 航空学院,西安 710072)
结构受到外部激励总会产生不同的振动响应,绝大部分结构的疲劳失效都与振动有关,当振动频率与结构模态频率相当时,即可视为振动疲劳问题.周敏亮等[1]对国内外主要振动疲劳分析方法进行了归纳整理, 为飞机设计和维修提供振动疲劳的设计与分析技术支持文献.在工程实际中,随机振动是一种相对常见的振动形式,由于载荷随时间变化的规律预先无法确定,很难用确定性的时间或空间坐标函数描述,而只能用概率统计的方法描述.通过随机振动响应分析,获得结构的应力响应功率谱密度函数(Power Spectral Density,简称PSD),由PSD可求得应力范围的概率密度函数(Probability Density Function,简称PDF),通过PDF可求得结构危险部位的疲劳累积损伤和疲劳寿命.
为了估算随机振动环境下结构的疲劳寿命,王明珠等[2]提出了一种结构随机振动疲劳寿命估算的样本法,通过该样本法能够处理在频域内基于谱密度描述的宽带随机振动.安刚等[3]讨论了随机振动响应的统计特性分析、结构响应的动应力与常规疲劳载荷的关系,完成了用功率谱密度表示的随机振动载荷作用下的悬臂梁结构的响应分析以及疲劳寿命估计.孟凡涛等[4]采用基于功率谱密度函数估算结构振动疲劳的方法,分析了某型机翼在随机振动载荷下的强度特性.Roberto Tovo[5]总结了宽带载荷激励下疲劳损伤的预估方法,研究了频域内疲劳损伤与不同的载荷计数法之间的关系,并提出了一种寿命预估方法,该方法可以较准确地预估宽带及窄带高斯载荷下的疲劳寿命.曹明红等[6-7]研究了常见的宽带随机振动疲劳寿命频域估算方法,并且验证了各种频域估算方法的适用性和估算精度.H·Y·Liou等[8]基于随机振动理论考虑的塑性相互损伤准则,提出了一个用于估计结构疲劳寿命的修正模型.孟彩茹等[9]基于功率谱密度函数对随机载荷下的振动构件进行疲劳寿命估算,分别讨论了窄带随机载荷和宽带随机载荷两种情况.张积亭等[10]提出利用随机响应功率谱密度求出的特征频率作为平均频率,在求解疲劳损伤量时比较方便.
结构处于宽频随机载荷环境中时,激励带宽内将包含结构的多阶固有频率,很可能会激起结构多阶共振响应.由于高阶响应应力的参与,结构局部区域的动应力会急剧增加,可能会瞬间引起结构发生裂纹或失效.工程分析中,通常认为振动疲劳破坏往往以结构一阶固有频率共振破坏为主,其他阶次的影响相对较小,这就忽略了高阶响应应力对结构造成的损伤,导致对损伤估计不足或寿命偏高.林莎等[11]通过试验表明,高阶响应在一定程度上缩短结构振动疲劳寿命,且响应值越大,对寿命的影响也越大.研究高、低阶频率响应对寿命的影响,通常将随机载荷分解为以各阶固有频率为中心的窄带载荷的组合,经典的Bi-modal法[12-14]就是一种适用于双模态随机振动疲劳寿命估算的方法.
本文针对典型铝合金薄板结构,根据Miner累积损伤理论和Dirlik疲劳寿命估算方法,计算在单窄带、双窄带和多窄带随机载荷激励下结构的振动疲劳寿命,分析高阶模态载荷对结构疲劳损伤和寿命的影响.
1 振动疲劳寿命估算的Dirlik方法
根据Miner线性损伤累积理论,疲劳损伤可以线性地累加,各个应力之间相互独立且互不相关,多级应力作用下结构的累积损伤为
(1)
其中:ns为应力幅值为S时的实际循环数,可用幅值概率密度函数P(S)表示,NS表示应力幅值为S时的破坏循环次数,可由S-N曲线方程确定.
ns=E(P)·T·P(S)
(2)
NS=C·S-m
(3)
其中:E(P)为随机响应信号峰值概率的期望值;T为随机响应时间;C、m为材料S-N曲线常数.
为了确定应力幅值的概率密度函数P(S),Dirlik 研究了70种不同形状的功率谱密度函数,提出了一个概率密度函数的经验公式.这个半经验公式由一个指数分布密度函数与两个Rayleigh分布密度函数叠加而成,该公式结果可以近似接近雨流计数法得到的结果,并且适用于任何类型功率谱.在该方法中,应力幅值概率密度函数是4个PSD惯性矩m0、m1、m2、m4的函数,其数学表达式为
(4)

将式(2)、(3)、(4)代入式(1),得到结构损伤为
(5)
一般情况下,认为当D=1时,结构发生破坏,由此可以得到结构的疲劳寿命
(6)
2 振动响应分析
2.1 固有模态分析
为避免正方形模型的模态振型对称性较高,选用长方形薄板模型.在MSC.Patran中建立薄板模型,具体尺寸为300×200×1.8 mm,长宽比为1.5∶1,边界条件为四边固支,如图1所示.

图1 薄板模型
材料为6061-T651铝合金,常规力学性能为:E=68.9 GPa,ρ=2800 kg/m3,σu=228 MPa,ν=0.33.借助MSC.Nastran计算得其前10阶固有频率(表1),对应的振型如图2所示.

表1 薄板模型前10阶固有频率
2.2 频率响应分析
放开模型沿厚度方向(z向)的位移约束,用带宽包括前10 阶固有频率(100~1500 Hz)的单位加速度载荷(1 m/s2)对结构进行扫频激励,模型的阻尼值参照试验值设定为ξ=0.01(通过正弦扫频振动试验及半功率带宽法计算得到).由应力分布(图3)可以确定结构的危险位置在长边的中心区域,绘制危险位置处(Node 31)的频率响应曲线如图4所示.由频率响应曲线可以看出,在包含结构前10阶固有频率的宽带中,模型的危险位置在第1、第4和第8阶固有频率附近各有一个峰值,且在1阶的响应值明显大于后面两阶.根据振动理论,结构共振状态下的应力响应往往以第1阶固有频率为主,其他阶次的影响相对较小.

图2 薄板模型前10阶振型
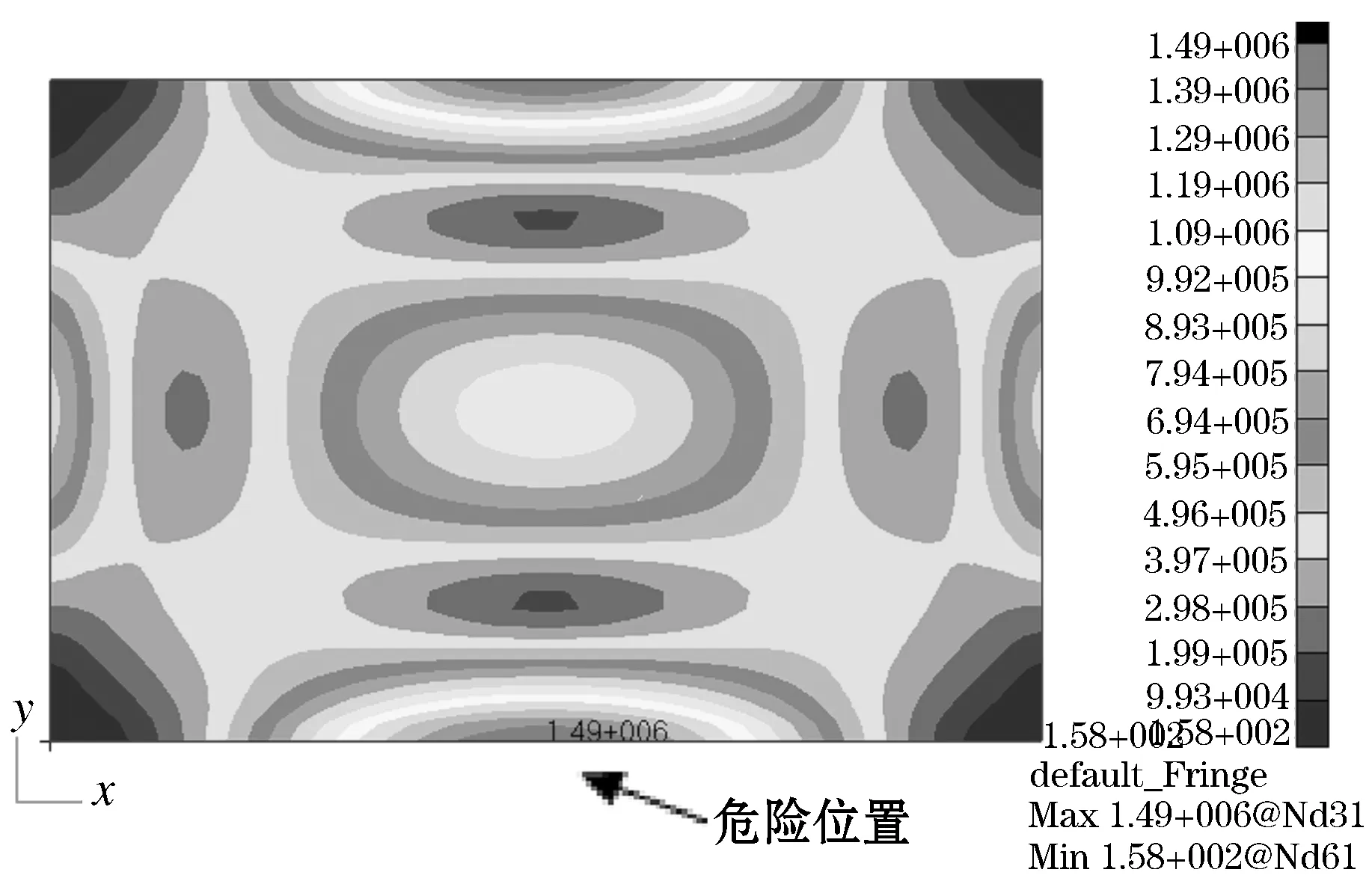
图3 频率f=289.38 Hz时模型上应力分布

图4 危险位置处的频率响应曲线
2.3 瞬态响应分析
计算出模型的固有频率后,分别施加频率为289.38 Hz(等于结构第1阶固有频率)和260 Hz(小于结构第1阶固有频率)的正弦加速度载荷对结构进行激励,以获取结构在共振和非共振状态下的应力响应.经计算可知,模型在激励频率为289.38 Hz、加速度幅值为12 g时,最大应力为125 MPa,如图5所示;在激励频率为260 Hz、加速度幅值为80 g时,其最大应力为125 MPa,如图6所示.可以看出,在共振状态下,只需很小的载荷就能激振出很大的应力幅值,这也说明共振状态下结构的响应应力急剧增高,对结构的危害也最大.
分别给模型施加上述两种载荷激励,从而保证在共振和非共振状态下模型上的最大应力相等,研究共振状态对结构振动疲劳寿命的影响.采用有限元软件MSC.Fatigue对模型进行振动疲劳分析,计算得知:在共振状态下,结构危险部位的疲劳寿命为7.41×103s;在非共振状态下,结构危险部位的疲劳寿命为8.51×103s,如图5、6所示.可以看出,虽然模型分别一直处于共振状态和非共振状态,但在两种不同状态下结构的疲劳寿命相差不大,这是因为激励加速度幅值的不同,保证了模型上的最大应力始终是一致的.根据Miner累积损伤理论,损伤是由一定幅值的应力所产生的,那么相同的应力幅值也必定产生同样的损伤,从而在相同的应力幅值下,两种状态下模型的振动疲劳寿命也必定是相同的.从两寿命云图上可以看到,模型上危险部位的位置、区域大小基本是一致的.因此,对于振动疲劳和非振动疲劳问题,其根本途径都是降低结构危险部位的最大应力,这样才能有效提高结构的疲劳寿命.
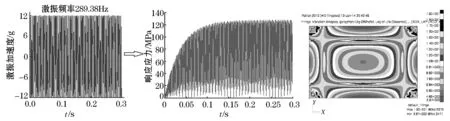
图5 共振状态下激励载荷、危险位置处的响应应力及疲劳寿命云图

图6 非共振状态下激励载荷、危险位置处响应应力及疲劳寿命云图
3 振动响应试验
随机振动响应试验在东菱5吨级电振动台(ET-50W-445)上进行,试样尺寸为340×240×1.8 mm的长方形薄板,四边各预留20 mm作为固支端并开孔.采用3个120 Ω应变花测量试样中心、长边和短边中点(距离边界10 mm)相应位置处的应变历程,通过1个安装在振动台水平台面上的加速度传感器来测量系统输入加速度,每个工况下振动响应试验持续时间约10 min,试验设备及试样加持如图7所示.采用数字图像相关方法(Digital Image Correction, DIC)对试样在随机振动载荷作用下的变形场进行测量,试验前在试样表面喷涂均匀颗粒状散斑,散斑是试件变形信息的载体,其颗粒尺寸和形状对DIC的测量精度有很重要的影响.试验中通过两个Phantom V711高速摄像机记录试样变形的全过程,每种工况保存1 000张照片用于分析试样上的应变场和位移场.

1—振动台;2—连接头;3—水平滑台;4—转接夹具;5—夹具;6—试样;7—加速度传感器;8—冷光灯;9—高速摄像机
首先进行正弦扫频试验,给试样施加一频率为100~1500 Hz、幅值为5 g的正弦加速度;随后进行随机响应试验,给试样施加一频率为260~300 Hz,加速度功率谱密度为1 g2/Hz的窄带随机载荷.
试验测得试样一阶固有频率为283.81 Hz,小于数值仿真结果289.38 Hz,这是由于有限元计算中模型的边界条件偏强,忽略了真实夹具上倒角的存在,使得模型有效面积略小于真实试样尺寸,另外模型的材料参数与试样的真实值也可能略有差别.
图8(A)、(B)分别给出了中心位置处RMS应力响应的试验值和仿真值,峰值应力均为20.3 MPa左右,两者相差不大.图9是采用DIC测得试样上的位移场分布,图10是对应的有限元仿真计算结果,对比发现中心位置最大位移的试验值为0.699 mm,仿真值为0.734 mm,两者之间的误差为4.8%.因此,有限元法计算动应力和位移是可信的.

图8 中心位置处RMS应力的试验值和仿真值

图9 试样的位移场分布(DIC试验结果)

图10 模型的位移场分布(仿真结果)
4 振动疲劳分析
首先,给模型施加频率以各阶固有频率为中心±20 Hz,功率谱密度为2 g2/Hz的单窄带随机载荷(加速度均方根为8.94 g),采用MSC.Fatigue分别计算出前10阶模态中只有其中某一阶共振时的疲劳寿命.然后,给模型施加频率以第1阶与某一高阶固有频率为中心±20 Hz,功率谱密度均为2 g2/Hz的双窄带随机载荷(加速度均方根为12.65 g),计算同时激起两阶共振时的疲劳寿命.最后,给模型施加频率以第1阶、第4阶、第8阶为中心±20 Hz,功率谱密度均为2 g2/Hz的多窄带随机载荷(加速度均方根为15.49 g),计算同时激起三阶共振时的疲劳寿命.
由表2可知,单独激起第1阶共振时的寿命为3.48×104s,而单独激起其他各高阶振动时的疲劳寿命均大于4.58×1010s.当第1阶与第4阶或第8阶叠加加载后,结构疲劳寿命下降明显,疲劳寿命分别为2.35×104s和1.23×104 s,而与其他高阶模态载荷叠加加载后模型疲劳寿命基本不变.当第1、第4与第8阶模态载荷同时加载时,其疲劳寿命再次下降,变为9.77×103s.
由此并不是每个高阶模态载荷与一阶载荷叠加后都会使得模型疲劳寿命下降,这说明疲劳寿命的下降并不是由于激励能量(加速度均方根)的增加所导致的.由模态分析可知,在第1、第4以及第8阶振型的中心位置处均有一个峰值,于是当第4阶或第8阶与第1阶振型被同时激起时,它们会同时产生峰值响应,这样就相当于在低频峰值上叠加高频峰值,高、低频模态之间的耦合作用,对模型产生更大的损伤,使得其疲劳寿命明显下降.
分析模型的单位时间损伤量可知,当第1阶模态载荷单独加载时损伤量为2.87×10-5,其余高阶模态载荷单独加载时损伤量几乎为0.而在第1阶与第4阶模态载荷同时加载时损伤量为3.95×10-5,在第1阶与第8阶模态载荷同时加载时损伤量为8.13×10-5,在第1阶、第4阶与第8阶模态载荷共同加载时损伤量为1.02×10-4.这充分说明,虽然高阶模态载荷单独作用时对结构几乎没有损伤,但是高、低阶模态载荷叠加加载对结构造成的损伤量却可能远大于两者单独加载对结构所造成损伤的叠加和.因此,在宽频随机振动环境下,高阶模态产生的损伤不可忽略.

表2 各种随机载荷激励下结构危险位置单位时间损伤量及疲劳寿命
5 结 论
本文通过振动响应试验和数值分析手段研究了铝合金薄板多模态随机振动特性.通过振动响应试验验证了数值计算结构振动应力的准确性,通过数值模拟研究了结构的频率响应、瞬态响应、随机响应和疲劳特性,可得出以下结论:
1)阻尼一定时,振动应力是决定结构疲劳寿命的主要因素,根据Miner线性损伤理论可对结构损伤和疲劳寿命进行预估.
2)宽频多窄带(每个窄带包含结构某一阶固有频率)随机载荷对结构造成的损伤可能远大于这些窄带先后单独对结构造成损伤的叠加和.
3)结构受到宽频随机振动载荷激励时,高阶载荷激励会对结构的疲劳寿命产生较大影响,仅考虑一阶模态响应容易导致寿命估算偏高.
参考文献:
[1] 周敏亮, 陈忠明. 飞机结构的随机振动疲劳分析方法[J]. 飞机设计, 2008, 28(2): 46-49.
[2] 王明珠, 姚卫星, 孙 伟. 结构随机振动疲劳寿命估算的样本法[J]. 中国机械工程, 2008, 19(8): 972-975.
[3] 安 刚, 龚鑫茂. 随机振动环境下结构的疲劳失效分析[J]. 机械科学与技术, 2000, 19(S1): 40-42.
[4] 孟凡涛, 胡愉愉. 基于频域法的随机振动载荷下飞机结构疲劳分析[J]. 南京航空航天大学学报, 2012, 44(1): 32-36.
[5] TOVO R. Cycle distribution and fatigue damage under broad-band random loading [J]. International Journal of Fatigue, 2002, 24(11): 1137-1147.
[6] 曹明红, 邵 闯, 齐丕骞. 宽带随机振动疲劳寿命的频域分析与试验对比研究[J]. 机械科学与技术, 2013, 32(6): 839-844.
[7] 曹明红, 葛 森, 齐丕骞. 随机振动疲劳频域分析方法的对比研究[J]. 振动工程学报, 2008, S: 94-98.
[8] LIOU H Y, WU W F, SHIN C S. A modified model for the estimation of fatigue life derived from random vibration theory [J]. Probabilistic engineering mechanics, 1999, 14(3): 281-288.
[9] 孟彩茹, 卢博友. 基于PSD的随机载荷下振动疲劳寿命估算[J]. 机械设计, 2009, 26(5): 73-75.
[10] 张积亭, 周苏枫. 飞机典型构件振动疲劳寿命分析[J]. 机械科学与技术, 2002, S: 3-16.
[11] 林 莎, 施荣明. 高阶响应对振动疲劳寿命的影响研究[J]. 振动工程学报, 2010, S: 153-156.
[12] FU T T, CEBON D. Predicting fatigue lives for bi-modal stress spectral densities [J]. International Journal of Fatigue, 2000, 22(1):11-21.
[13] BRACCESI C,CIANETTI F, LORI G.Fatigue behaviour analysis of mechanical components subject to random bimodal stress process: frequency domain approach [J]. International Journal of Fatigue, 2005, 4: 335-345.
[14] LOW Y M. A method for accurate estimation of the fatigue damage induced by bimodal processes [J]. Probabilistic Engineering Mechanics,2010, 25(1):75-85.
