淮海城市群空间范围的综合界定

2014-09-13欧向军

江苏师范大学学报(自然科学版) 2014年4期

欧向军

(江苏师范大学城市与环境学院,江苏徐州 221116)

城市群是指在特定地域范围内由相当数量的不同性质、类型和等级规模的城市所构成的相对完整的城市集合体．中国正进入快速城市化时期,城市群已成为未来新型城镇化发展的主体形态,也是未来经济发展中最具活力和潜力的核心增长极点[1]．城市群空间范围界定是城市群研究的基础,不同的发展阶段与水平、不同的研究视角和需要,城市群的空间范围会有所不同,即城市群的区域边界具有动态性、阶段性和模糊性．尽管如此,国内外学者还是从不同角度对城市群空间范围的识别与划分进行了详细而深入的分析．如Gottmann早在1957年就在研究美国东北海岸区城市化的基础上提出了城市群空间范围判定的5个标准[2],Martin通过城市场对爱尔兰城市群的空间组合区域进行了划分[3],Mu等基于积权重Voronoi图对美国城市群的空间范围和格局体系进行了研究[4],等等．国内关于城市群空间范围的研究主要以定性分析为主,定量研究相对较少.其中定性分析主要依据城市群判定标准并结合经济社会统计年鉴资料,对城市群的空间范围进行识别划分[5-8];定量研究主要依据相关模型,并结合一些社会经济指标对城市群的空间范围进行理论界定,具体的模型方法主要有城市群发育程度指数模型[9],城市综合实力的引力模型[10]、重力模型[11]、摩擦系数模型[12]和场能模型[13]等,这些方法为不同规模城市群的空间范围界定提供了相应的定量分析依据．而城市群空间范围的界定,既是一个理论研究问题,也是一个实践操作问题[10]．为此,本文在对城市群核心依托的中心城市影响力进行综合分析的基础上,依据空间相互作用的引力模型和断裂点模型,对淮海城市群的空间范围进行了理论界定,并结合淮海核心区一体化建设实践和地域邻近的实际情况,进一步对淮海城市群的空间范围进行综合界定．这对于科学、规范地确定淮海城市群空间范围,加快淮海城市群一体化建设,提升其在淮海经济区和全国发展中的地位,促进我国东部沿海都市连绵区形成与发展,具有重要的理论意义和现实价值．

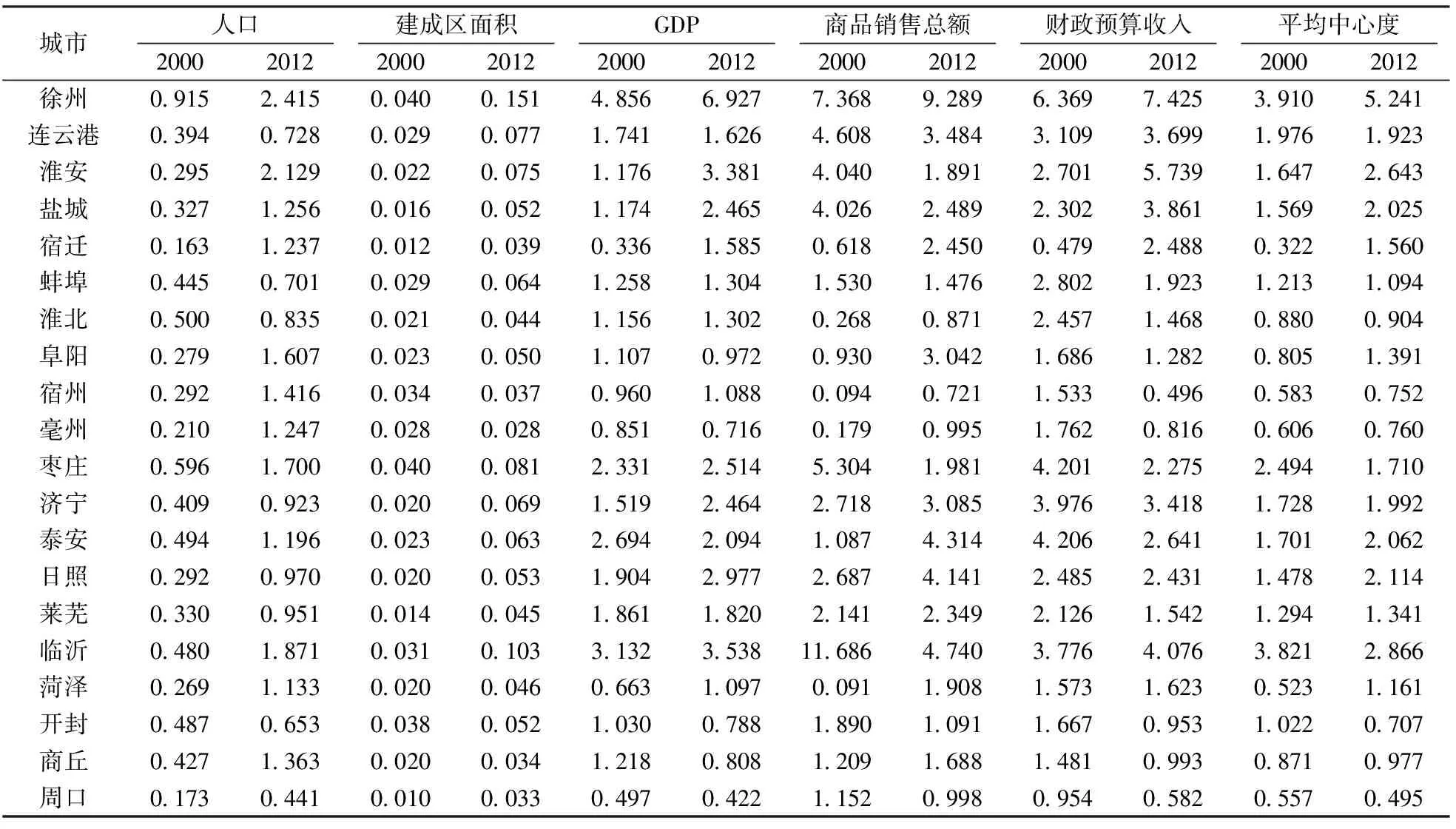
表1 淮海经济区主要城市中心度

注:平均中心度分别为前5项城市中心度之和的平均值

1 中心城市的影响力比较

城市群是指以中心城市为核心向周围辐射构成的多个城市的集合体[14],中心城市是城市群形成与发展的核心和依托,中心城市的综合实力越强,其组织带动周边地区发展的能力就越大,辐射与吸引的范围就越广,城市群的空间影响范围也就相对越大．因此,科学识别城市群的空间范围,必须要对其所依托的中心城市影响力进行综合考察．为此,本文从城市的中心度和综合实力两个方面,对主要中心城市的影响力进行比较分析,判断并确定淮海城市群的中心城市,从而为其空间范围的综合界定提供前提支撑条件．

1.1 城市中心度多指标评价

城市中心度能够反映该城市在其辐射吸引区域中发挥中心职能的作用大小,通常以一个城市的某项指标占其所在比较地区该指标总和的百分比来表示[15]．淮海城市群作为淮海经济区的先行发展区,其中心城市必然也是淮海经济区的发展中心,故以淮海经济区为比较地区,人口、建成区面积、地区生产总值(GDP)、商品销售总额和财政预算收入(文中数据除特殊说明外，均来源于《中国城市统计年鉴2001》和《中国城市统计年鉴2013》)为评价指标,对其20个地级市市区的2000年和2012年的城市中心度进行多方面比较分析,见表1．

2012年,徐州在5个方面的中心度均排在首位．从区域来看,明显存在两个层次,苏北与鲁南地区的城市中心度要远高于豫东和皖北地区,平均中心度排在前10位的全部为苏北与鲁南地区的城市,依次为徐州、临沂、淮安、日照、泰安、盐城、济宁、连云港、枣庄和宿迁,其中有5个与徐州相接壤,且徐州城市中心度是排在第2位临沂的1.83倍．就具体指标而言,GDP和财政预算收入这2个指标的城市中心度排在前10位的均为苏北与鲁南地区的城市,建成区面积和商品销售总额这2个指标的城市中心度排在前10位的也均有9个为苏北与鲁南地区的城市,人口指标城市中心度差别不大．从淮海经济区主要城市的中心度变化来看,2000～2012年间,徐州各项指标的城市中心度均有了较大提升,尤其是GDP的城市中心度变化最大,表明徐州城市经济中心的地位提升最快．另外,淮海经济区20个地级市市区人口和建成区面积的城市中心度均有较大提升,这与大中城市为主要载体的城镇化发展道路密切相关．

显然,无论从人口与建成区面积规模,还是从经济生产和生活服务总量来看,徐州在淮海经济区的城市中心度均排在首位,且呈显著提升趋势,表明徐州在淮海经济区的首要中心城市地位进一步提升,区域发展的核心作用进一步彰显．

1.2 城市实力的综合分析

受多种因素影响,城市的综合实力也表现在许多方面．为此,尽量遵循指标选取的系统性、完整性、有效性和可量可比性等原则,并在借鉴前人相关研究的基础上,从城市规模、经济增长、社会发展、开放创新和设施保障5个方面,选取20个指标,建立起城市实力的综合评价指标体系(表2),力求较为全面准确地反映各个城市实力的综合水平．运用熵值法确定各个指标权重值,并根据各评价指标权重及其归一化的值,分别计算出2012年淮海经济区20个城市的城市规模实力、经济增长实力、社会发展实力、开放创新实力和设施保障实力及其综合实力的得分,见表3．

表2 城市综合实力评价指标体系

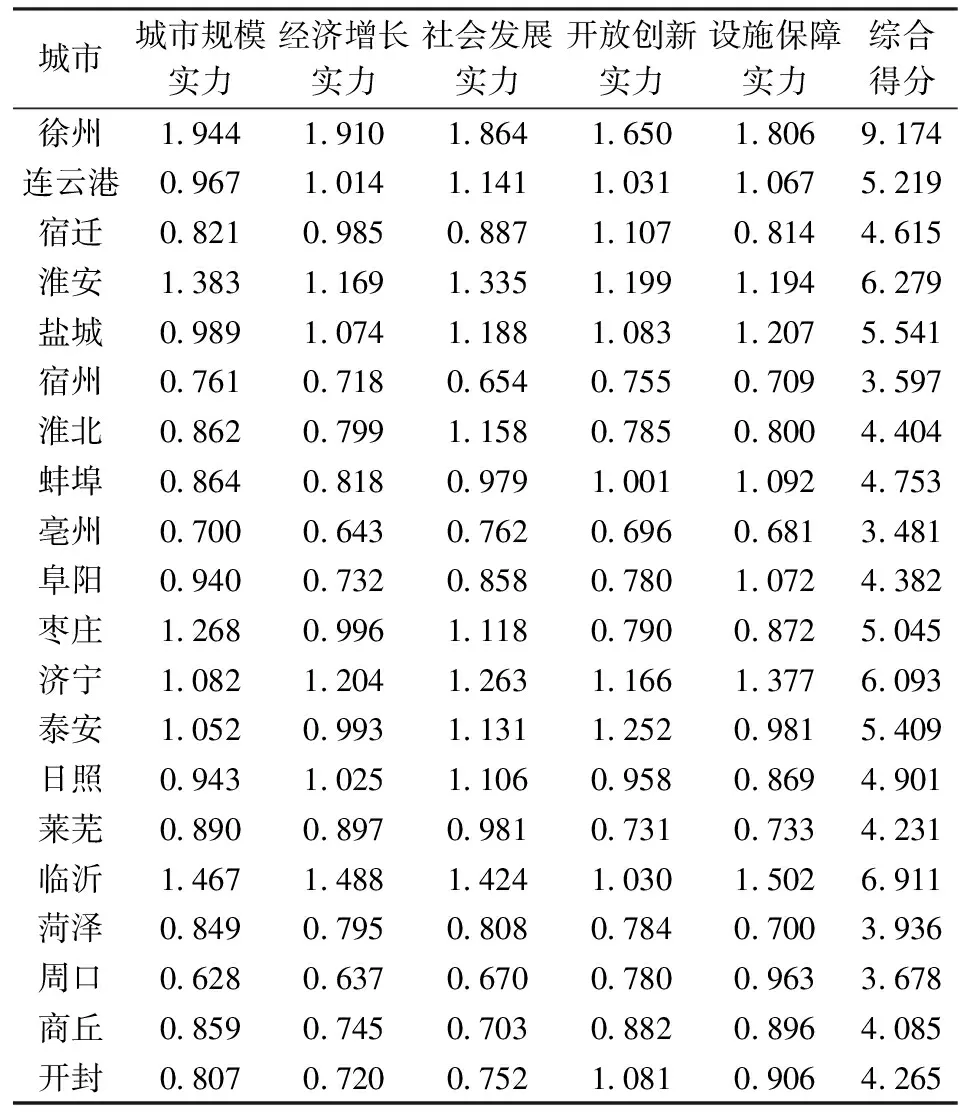
表3 淮海经济区主要城市的综合实力得分

由表3知,徐州在城市规模、经济增长、社会发展、开放创新和设施保障5个方面的实力得分均排在首位,从而使其城市综合实力的得分远高于淮海经济区的其他城市．从各城市实力的综合得分来看,淮海经济区20个地级城市可以划分为4个等级:第一等级的城市是徐州,它是淮海经济区的核心城市,其城市实力最强,综合得分为9.174;第二等级的城市为临沂、淮安和济宁,城市实力次之,综合得分在6.1～7.0之间;第三等级的城市有盐城、泰安、连云港、枣庄、日照、蚌埠和宿迁,城市实力中等,综合得分在4.6～5.5之间;第四等级的城市包括淮北、阜阳、开封、莱芜、商丘、菏泽、周口、宿州和亳州,城市实力较弱,综合得分在3.5～4.5之间,除莱芜和菏泽外,全部为皖北和豫东地区的城市．

综上所述,无论是从城市中心度,还是从城市综合实力来看,徐州均是淮海经济区的首要中心城市,且其他城市与徐州均存在着较大的差距,空间上呈现典型的首位分布特征．

2 城市群的空间范围界定

2.1 基于引力模型的城市群空间范围识别

城市群是由相互作用、相互依赖的若干个城市结合而成的具有特定功能的城市综合体,是城市之间空间联系与作用的产物．因此,地域邻近的城市之间联系紧密与否,是识别城市群空间范围大小的重要因素,即可以通过分析城市之间经济联系强度的大小来界定这些城市是否属于城市群．区域经济联系主要表现为经济实体区域间的相互作用和关联,而引力模型是测算区域联系最为常用的方法．本文主要是测算与评价城市间的经济联系,经济总量必然是首选指标,而人与土地作为经济活动的主体和载体,城镇人口与建成区面积当然是评价城市相互联系的重要指标,故采用修正的引力模型对淮海经济区20个地级城市之间的经济联系程度进行测算.引力模型及其相关表达式为[16]

(1)

(2)

式中:Pi,Pj分别为城市i,j的市区人口;Vi,Vj分别是城市i,j的市区国内生产总值;Si,Sj分别为城市i,j的建成区面积;Dij为城市i,j间的最短公路交通里程(来自百度地图所测度的最短交通线距离);Fij是城市i对城市j的空间相互作用量,又称经济联系量,反映的是两者之间的经济联系程度;Fi为在引力模型的基础上测算城市i与其他所有城市的经济联系量之和,即城市i对外经济联系的总量,其值大小可以反映城市i与其他城市经济联系的疏密程度．

表4 淮海经济区的区域经济联系强度

据公式(1)和(2),依次计算出2012年淮海经济区20个地级城市的相互经济联系量和各自对外经济联系总量,用以表述各城市的经济联系强度．受经济发展水平、城市人口与建成区规模以及交通距离的影响,淮海经济区主要城市对外经济联系总量呈现出显著的“中心-外围”模式和区域差异特征(图1)．对外经济联系总量排在第1位的徐州是第2位枣庄的1.8倍,是末位周口的22.3倍,首位城市地位非常突出,并在空间上以徐州为中心依次向四周逐渐递减,呈现“中心-外围”式的分布特征．从经济联系总体强度来看(表4),苏北和鲁南远大于皖北和豫东,鲁南7市的经济联系总量最大,豫东3市最小．其中,鲁南内部城市经济联系最为紧密,约占其经济联系总量的51.5%;苏北城市与鲁南经济联系较为紧密,约占其经济联系总量的36.2%,且高于其内部城市经济联系的紧密程度;皖北城市与苏北经济联系较为紧密,约占其经济联系总量的41.3%,但与豫东和鲁南经济联系较小;豫东城市经济联系最为松散,且主要表现为与鲁南和皖北之间的联系,与苏北及其自身内部联系较弱．

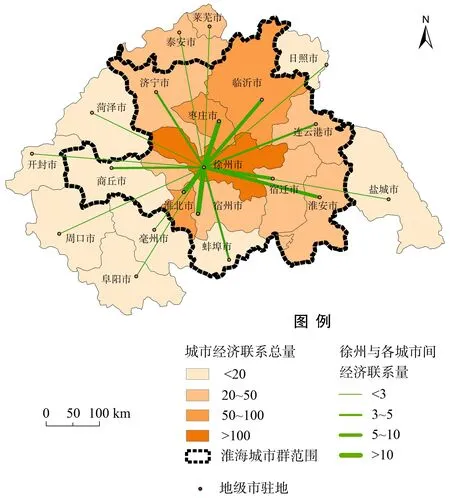
图1 淮海经济区主要城市经济联系的空间作用示意图

徐州经济联系总量最大,表明其与其他城市之间的联系最为紧密.按照各个城市与徐州之间经济联系量的大小进行排序,把与徐州经济联系量累计达到其对外经济联系总量85%的城市作为淮海城市群内的主要成员.结果表明,这样城市共有10个,且它们与徐州之间的经济联系量均在3个经济度之上(图1),分别是枣庄、淮北、宿州、宿迁、临沂、淮安、济宁、蚌埠、商丘和连云港,它们与徐州之间的距离均在200 km范围以内,且枣庄、淮北和宿州3个城市与徐州联系最为紧密,经济联系量均在15个经济度之上,累计占徐州对外经济联系总量一半以上(56.6%),与徐州一起构成淮海城市群的核心区,其他7市则构成淮海城市群的影响区．

2.2 基于断裂点模型的城市群空间范围识别

断裂点模型认为城市对周围区域的影响力与城市规模成正比,与至城市之间距离成反比,常被用来划分中心城市的吸引辐射腹地分界.而中心城市吸引辐射的腹地大小也是影响城市群空间范围的重要因素之一．因此,断裂点模型可以作为划分城市群空间范围的重要理论依据.若将该两相邻城市i,j间的吸引力平衡点定义为断裂点x,则点x满足[11]

(3)

式中:Dix为x点距i城市的距离;Si,Sj分别是城市i,j的“质量”,通常用城市的人口规模或经济总量来表示．但断裂点理论模型在实际应用中,存在着较大的局限性,主要由于城市人口或经济总量无法比较全面真实地反映城市规模与吸引力．因此,本文以城市综合实力来表示城市i,j的“质量”Si和Sj,并根据公式(3),分别计算出首要中心城市徐州与淮海经济区内其他各城市间吸引力断裂点x的距离Dix,结果见图2．

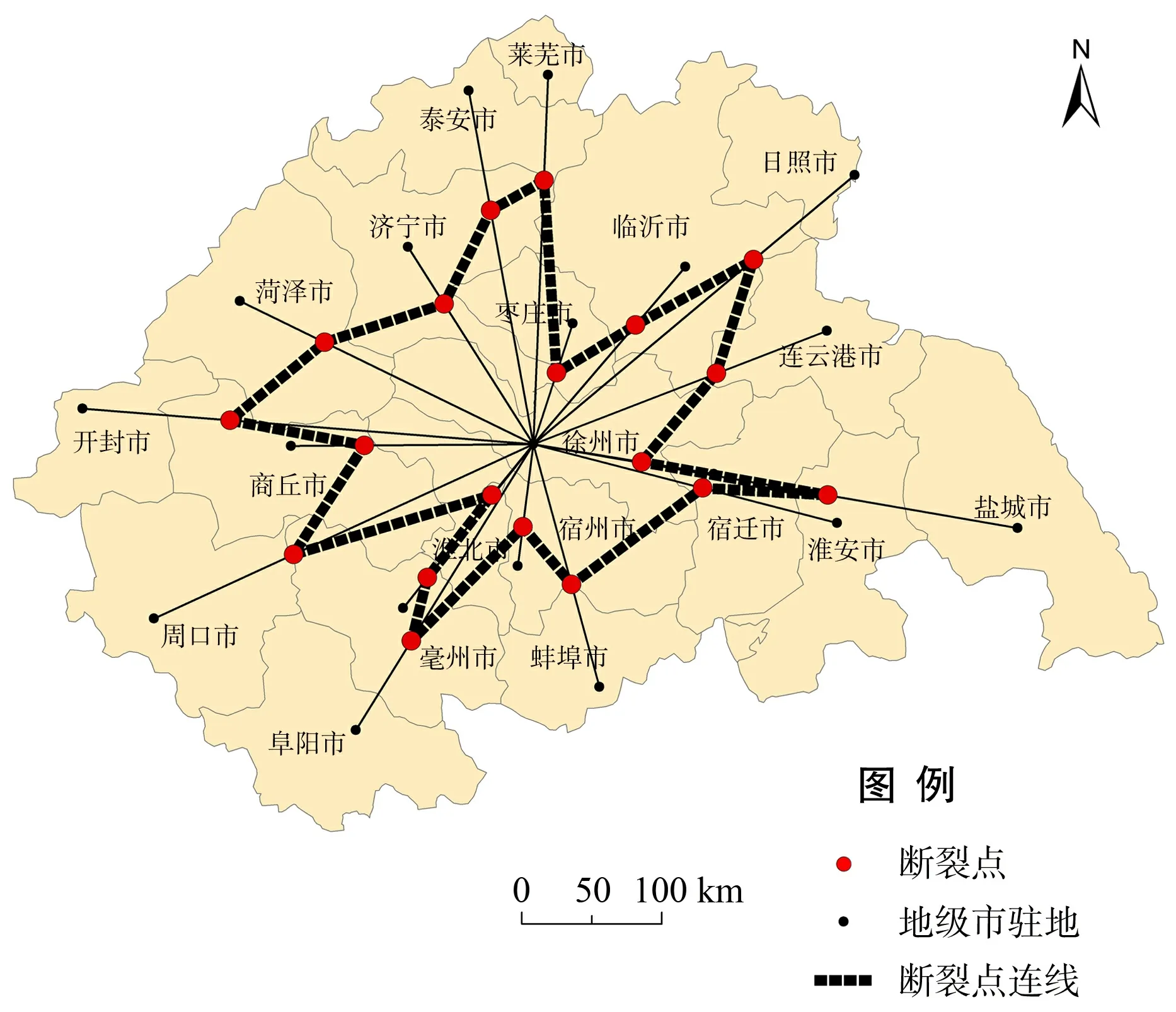
图2 徐州在淮海经济区的空间吸引范围

对断裂点公式的计算结果,通常的处理方法是:如果断裂点落在该城市的行政区边界范围之内,该城市就属于另一城市的吸引范围[11]．按照这个方法,从图2中可以看出,淮海经济区内的盐城、日照、莱芜、泰安、开封、周口、阜阳和蚌埠8个城市都不在首要中心城市徐州的直接吸引力范围之内,故以徐州为核心的淮海城市群的空间范围包括枣庄、淮北、宿州、临沂、宿迁、济宁、商丘、亳州、淮安、连云港和菏泽,共12个城市．

2.3 淮海城市群空间范围的综合分析

对城市中心度和城市综合实力两个方面的分析均表明,徐州市为淮海经济区的首要中心城市．在此基础上,依据中心城市吸引辐射、区内紧密联系和兼顾行政区界完整等原则,通过引力模型的城市经济联系强度分析,界定淮海城市群的空间范围,包括徐州、枣庄、淮北、宿州、宿迁、临沂、淮安、济宁、蚌埠、商丘和连云港共11个城市;通过断裂点模型的城市吸引辐射腹地范围划分,界定淮海城市群的空间范围,包括徐州、枣庄、淮北、宿州、临沂、宿迁、济宁、商丘、亳州、淮安、连云港和菏泽共12个城市．取以上2种方法的交集,理论上计算出的淮海城市群的空间范围包括徐州、枣庄、淮北、宿州、宿迁、临沂、淮安、济宁、商丘和连云港,共10个城市．

另一方面,2010年5月,在徐州召开的第一届淮海经济区核心区城市市长会议上共同签署了《关于加快淮海经济区核心区一体化建设的意见》[17],提出了淮海核心区范围,主要包括徐州、连云港、宿州、商丘、济宁、枣庄、宿迁和淮北8个城市.这与相关理论模型识别出的淮海城市群空间范围相比,缺少了临沂和淮安两个城市．

同时,地域邻近性既是城市群的重要特征之一,也是划分城市群范围边界的重要依据.淮海经济区中,与首要中心城市徐州直接相接壤的有枣庄、淮北、宿州、宿迁、临沂、济宁和连云港,共7个城市．

综合引力模型、断裂点公式、淮海核心区和地域邻近性4个方面的情况,将出现概率超过一半以上的城市划归为淮海城市群的范围之内,则淮海城市群的空间范围可以综合界定为徐州、临沂、济宁、连云港、宿迁、宿州、枣庄、淮北和商丘,共9个城市及其所辖县市,见图3．

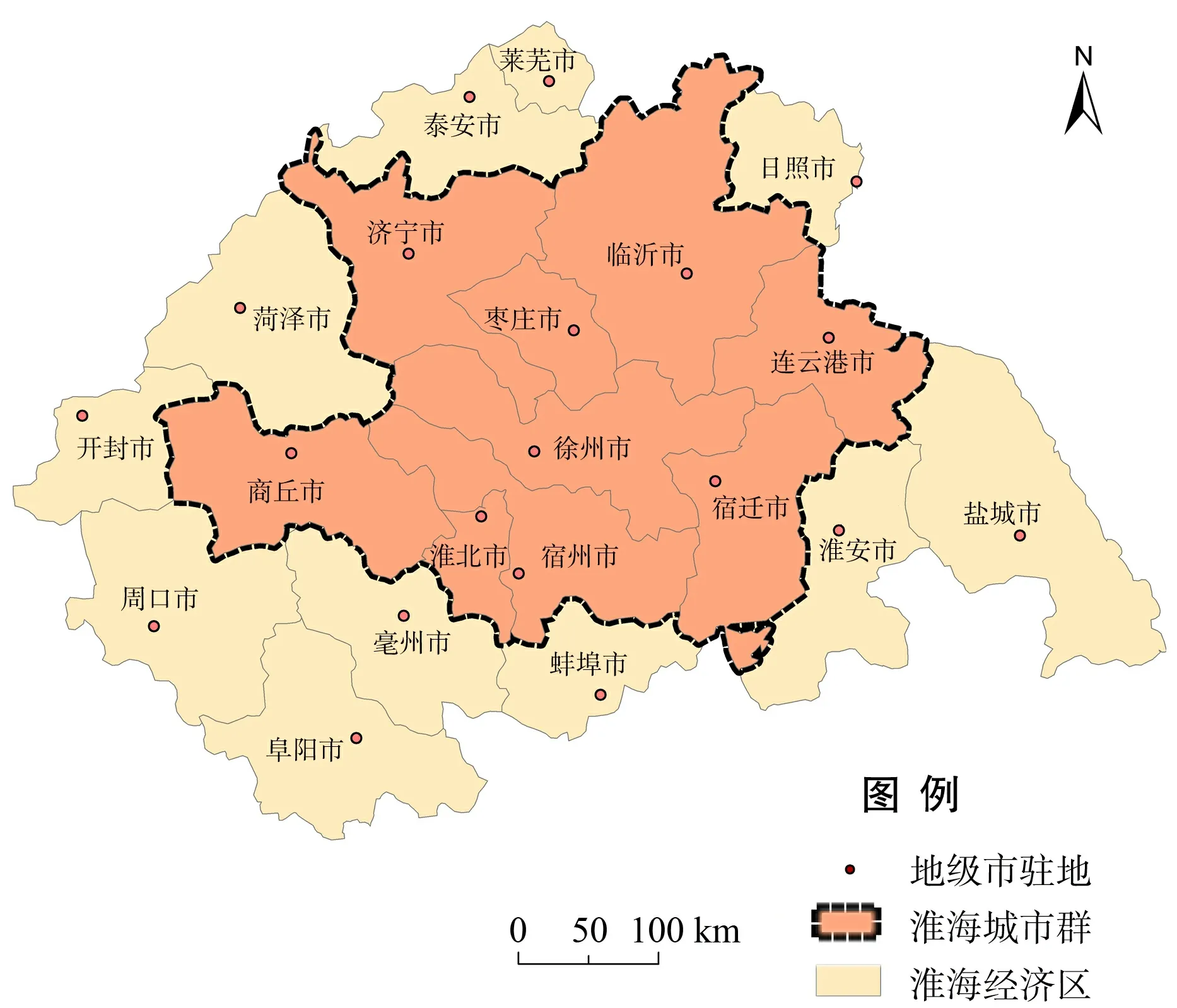
图3 淮海城市群的空间范围

3 主要结论

城市群空间范围的界定是城市群研究的基础,中心城市则是城市群形成与发展的核心和依托．为此,本文通过中心城市影响力分析,依据空间作用相关模型,确定城市间相互联系强度,划分中心城市的吸引辐射腹地,提出淮海城市群理论上的空间范围,结合淮海核心区一体化建设实践和地域邻近实际情况,进一步对淮海城市群的空间范围进行综合界定．主要结论如下:

1) 徐州中心城市的影响力最强．无论是从城市中心度的多指标评价,还是从城市实力的综合分析,徐州均是淮海经济区的首要中心城市,无疑是淮海城市群的核心城市．

2) 通过引力模型分析城市间经济联系紧密程度,发现徐州对外经济联系总量最大,其中,85%的联系量发生在枣庄、淮北、宿州、宿迁、临沂、淮安、济宁、蚌埠、商丘和连云港10个城市,且它们与徐州之间的经济联系量均在3个经济度之上,表明徐州与它们的经济联系最为紧密．

3) 通过断裂点模型,依据城市的综合实力,划分出淮海经济区首要中心城市徐州与其他城市间吸引辐射的腹地范围,发现徐州的直接吸引力范围包括:枣庄、淮北、宿州、临沂、宿迁、济宁、商丘、亳州、淮安、连云港和菏泽．

4) 综合引力模型与断裂点模型所划城市群空间范围的交集,划分出淮海城市群理论上的空间范围,包括徐州、枣庄、淮北、宿州、宿迁、临沂、淮安、济宁、商丘和连云港共10个城市;参照淮海核心区一体化的建设实践和地域邻近的实际情况,综合界定出淮海城市群的空间范围为徐州、枣庄、淮北、宿州、宿迁、临沂、济宁、商丘和连云港共9个城市．

参考文献:

[1] 方创琳.城市群空间范围识别标准的研究进展与基本判断[J].城市规划学刊,2009(4):1.

[2] Gottmann J.Megalopolis or the urbanization of the northeastern seaboard[J].Econ Geogr,1957,33(7):189.

[3] Martin B S.The Irish urban system and its dynamics[R].Dubin:NUI Maynooth & Fitzpatrick Associates,2000.

[4] Mu L,Wang X.Population landscape:a geometric approach to study spatial patterns of the US urban hierarchy[J].Int J Geogr Inf Sci,2006,20(6):649.

[5] 姚士谋,陈振光,朱英明,等.中国城市群[M].合肥:中国科学技术大学出版社,2006:5-7.

[6] 倪鹏飞.中国城市竞争力报告[M].北京:社会科学文献出版社,2008:387-390.

[7] 周一星,史育龙.建立中国城市的实体地域概念[J].地理学报,1995,50(5):17.

[8] 代合治.中国城市群的界定及其分布研究[J].地域研究与开发,1998,17(2):40.

[9] 方创琳,宋吉涛,张蔷,等.中国城市群结构体系的组成与空间分异格局[J].地理学报,2005,60(5):827.

[10] 陈群元,宋玉祥.城市群空间范围的综合界定方法研究[J].地理科学,2010,30(5):660.

[11] 顾朝林,庞海峰.基于重力模型的中国城市体系空间联系与层域划分[J].地理研究,2008,27(1):1.