季节自回归求和移动平均模型在重庆市某老年群体医疗费用预测中的应用

徐飞龙 叶孟良 王润华

(重庆医科大学公共卫生与管理学院卫生统计与信息管理教研室，重庆 400016)

中国60岁及以上老年人口达1.78亿，占总人口的13.3%〔1〕，比2000年上升了2.93个百分点。医疗费用作为老年人群费用的主要支出，已成为重要经济负担，本课题拟采用自回归求和移动平均模型分析老年人医疗费用趋势。

1 资料与方法

1.1资料来源 整理2005年1月至2010年12月重庆市某老年群体医疗费用月度资料如表1。

1.2研究方法 求和自回归移动平均(ARIMA)模型〔2〕是由Box和Jenkins提出的著名时间序列预测方法，又称为Box-Jenkins模型。该模型是用于描述非平稳资料的一种方法，当时间序列含有季节变动趋势时可以建立ARIMA季节乘积模型。

ARIMA预测模型ARIMA(p，d，q)(P，D，Q)s〔3〕，其中p和q为自回归和移动平均阶数，d为差分次数，P和Q为季节性自回归和移动平均阶数，D为季节差分次数，s是季节周期。ARIMA建模有4个基本步骤〔4〕：①序列的平稳化。要求原始序列平稳，即均数与方差都不随时间变化，自相关系数只与时间间隔有关，而与所处时间无关；②模型识别〔5〕。根据时序图和自相关(ACF)图、偏相关(PACF)图确定；③参数统计和模型诊断。通过拟合优度检验得到统计量包括方差、对数似然函数值、赤池信息准则(AIC)及贝叶斯信息准则(BIC)，选用各种参数有统计意义的模型；④模型预测〔6〕。以2005～2010年的逐月人均医疗费用拟合模型，利用2011年的逐月人均医疗费用回代检验模型的预测效果，根据预测值得到95%可信区间，计算预测值与实际值的相对误差，以此判断模型的预测精度，并进一步预测2012年的逐月人均医疗费用。

1.3统计学方法 采用SPSS19.0建立逐月人均医疗费用数据库，并利用Time Series分析模块进行数据处理与建模〔7，8〕。

2 结 果

2.1序列的平稳化 将表1中2005～2010的逐月人均治疗费用做时间序列图(图1)，重庆市某老年群体逐月医疗费用呈现明显的整体上升趋势和周期性。在每年的4,5,10,11月出现波峰，但在每年的12,1,6,7月出现波谷。对原始序列作ACF，PACF图，发现它们均为缓慢拖尾衰减，可判断为非平稳序列，识别为ARIMA (p，d，q)模型。对原始数据进行正态性检验Shapiro-Wilk(t=0.973，P=0.131)，不能拒绝原始数据正态分布的假设，不需要对原始数据进行对数转换。

表1 2005～2011逐月人均医疗费用情况(元)

因此，只考虑对分别进行一次一般差分和季节差分以消除整体趋势和季节的影响，预处理后的时序图见图2，长期趋势和季节性基本消除，得到一个宽平稳的随机序列，符合ARIMA模型的平稳性要求。

2.2模型识别 根据差分变换的次数，可初步确定模型应该是以12个月为周期的综合了连续模型和季节模型的复合季节模型ARIMA(p，1，q)(P，1，Q)12〔6〕，其中p，q和P，Q是待定参数，分别为连续模型和季节模型的自回归阶数和移动平均阶数。由ACF(图3)及PACF图(图4)得到，序列经差分后ACF由于含有季节的周期性影响，呈近似一步截尾，PACF拖尾，可以提示p=0，q=1，可进一步确定模型为ARIMA(0，1，1)(P，1，Q)12。季节模型的P和Q判断较难，根据文献，参数>2阶的情况很少，可以分别取0,1,2，由低阶到高阶逐个实验，根据模型的拟合优度、残差的白噪声情况及系数间的相关性进行综合判断。

2.3参数估计和模型诊断 分别对P、Q取0,1,2，由低阶到高阶逐步试验，根据最小BIC准则，并且结合参数检验可知：ARIMA(0,1,1)(2,1,0)12拟合最优，其中BIC=13.663，R2=0.555，一阶非季节滑动平均参数MA1=0.894(t=9.715，P=0.000)，一阶自回归参数SAR1=-0.691(t=-4.234，P=0.000)，SAR2=-0.415(t=-2.109，P=0.048)，模型具有统计学意义，本模型残差序列Box-Ljunt统计结〔Q(18)=11.859，P=0.690〕显示统计量差异均无统计学意义，可以认为残差为白噪声，表明所选模型是恰当的。

2.4模型拟合和比较

2.4.1ARIMA模型的拟合运用模型ARIMA(0,1,1)(2,1,0)12，对2005～2010年的逐月人均医疗费用时间序列数据拟合，并对2011年1月至12月的逐月人均医疗费用进行预测，拟合情况如图5，该图显示了模型对2005～2010年数据的拟合值以及预测值的95%的可信区间，可见模型对实际值进行了较好的跟踪和预测，南值与预测值的动态趋势基本一致，表现出与实际值相似的升降规律。虽然各个月份的适人均医疗费用与预测值不完全一样，但基本落在95%CI范围内。用相对误差衡量预值和实际值差距大小，可以看出2011年的合计相对误差为4.06%。

2.4.2指数平滑法 (Winters相乘模型)的拟合 指数平滑法有助于预测存在趋势和/或季节的序列，此处数据同时体现上述两种特征所以我们考虑运用指数平滑法与ARIMA(0,1,1)(2,1,0)12进行比较。经过对指数平滑法的多次尝试，选择了Winters相乘法预测模型，拟合情况如图6，其中R2=0.631，BIC=13.194。

2.4.3两种预测方法比较 一方面，从拟合的效果来看，两者的R2、Normalized BIC相差不大，均能较好的包含样本数据的信息；但是另一方面，从预测精度来看，前者的相对误差普遍较小，平均相对误差〔9，10〕小于后者，预测精度高。综合考虑，选择ARIMA(0,1,1)(2,1,0)12模型用于逐月人均医疗费用的短期预测。见表2。

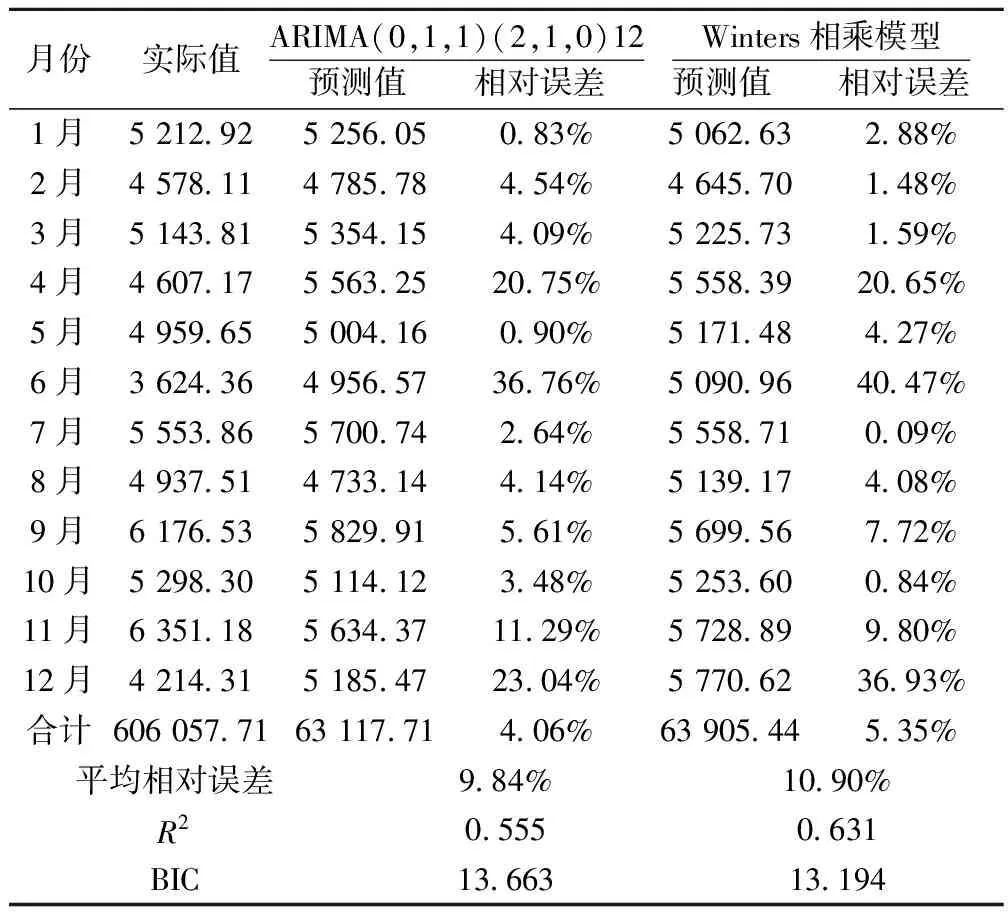
表2 ARIMA模型和Winters相乘模型的拟合情况比较

图1 原始序列图

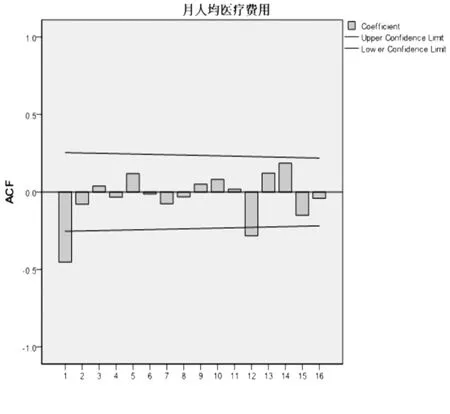
图3 一般差分和季节差分后的ACF图

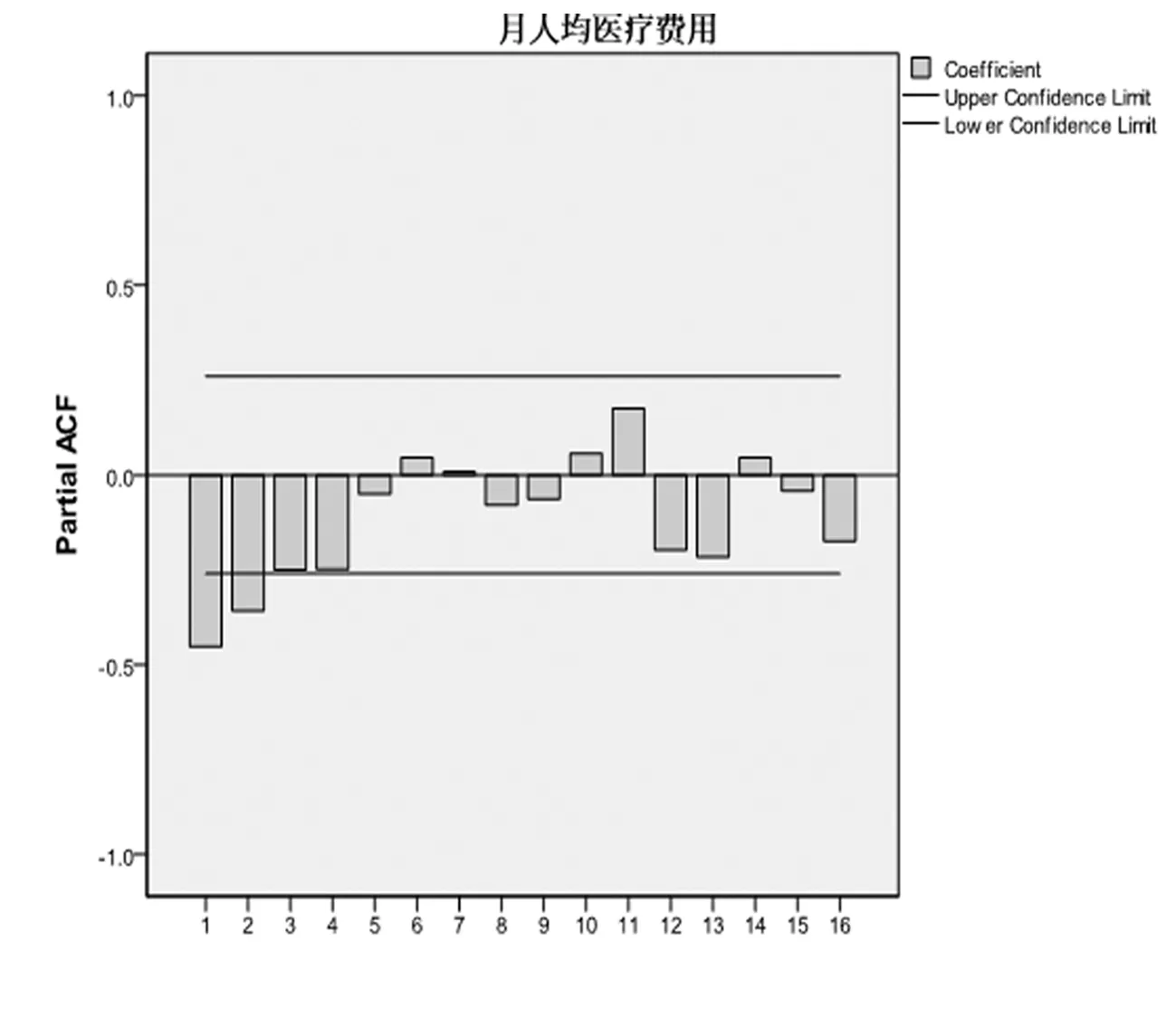
图4 一般差分和季节差分后的偏PACF图

图5 ARIMA模型

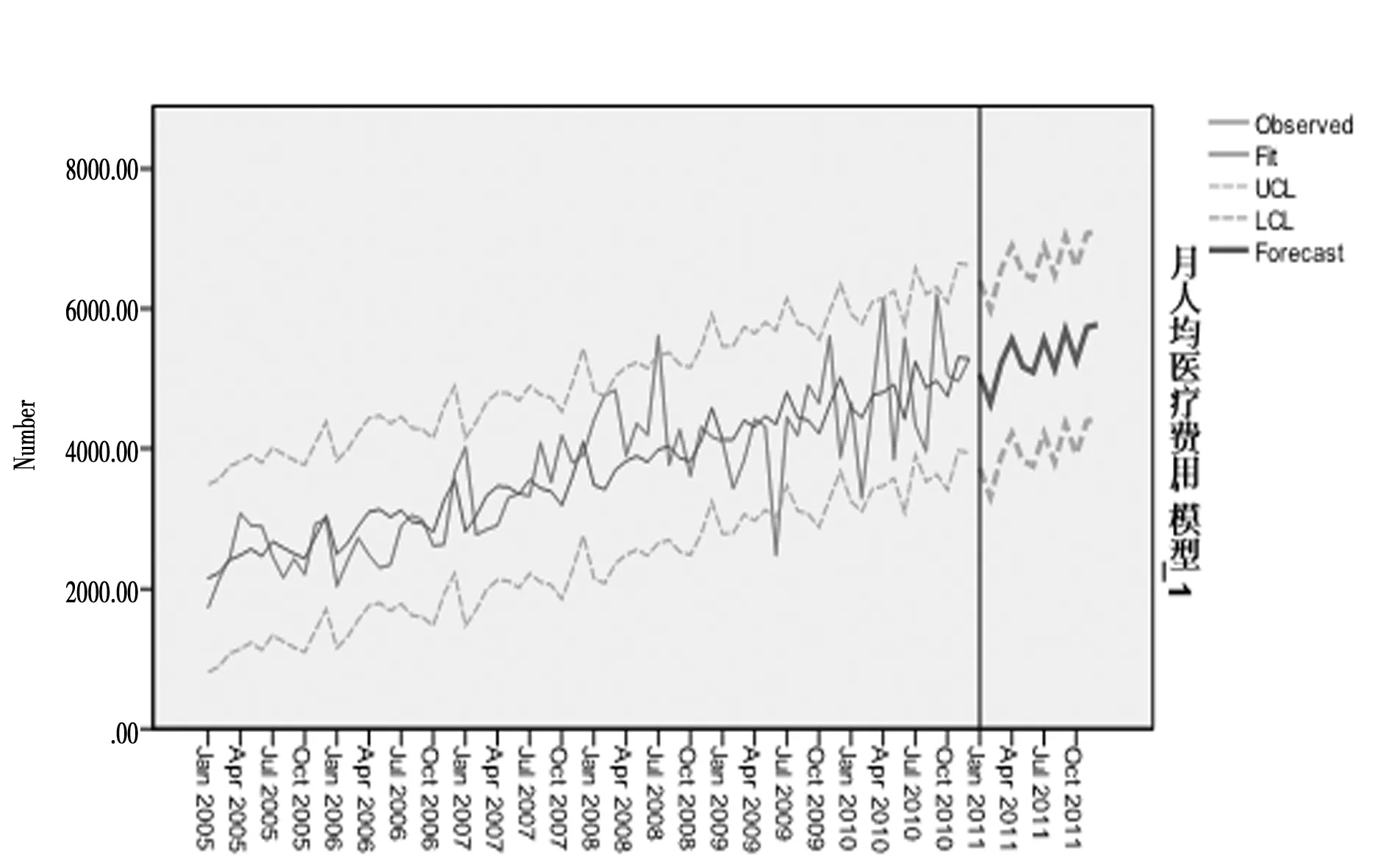
Winters相乘模型

3 讨 论

Winters相乘模型、ARIMA法都用于短期预测，当预测数据随时间呈现一种线性趋势和季节波动趋势时，两种方法均能提取很好地提取原始数据中的线性和季节信息，且能得到较好的拟合效果。但这两种方法针对不同的时间序列效果有所不同，Winters相乘模型是假设事物过去的发展规律会延展到未来，更多的利用近期的信息，因此就没有考虑到从过去到未来期间客观因素的影响，可能产生较大的预测误差，它也能较好的修正序列数据的季节性和趋势性，但由于近年来医疗改革的推动、医疗体制的变化，导致医疗费用发生了变化，预测精度有所下降；ARIMA模型则充分考虑了基本趋势、周期性、季节性、残差相关性等问题，使得预测精度提高，预测数据接近实际水平，尤其是短期预测方面，预测精度更高。而且利用SPSS、SAS等软件计算简单，预测结果直接输出，可选为医疗费用短期预测的最佳方法。

以上分析可知，重庆市某老年群体逐月人均医疗费用呈逐年增长趋势，这与近年来我国医疗体制的改革、经济发展、生活水平提高等有关系，与慢性病疾病模式的转变、高新医疗设备的应用、医疗服务于成本价格的不断提升、医疗保险覆盖面扩大后医疗服务利用的增加，以及群众健康期望值和医疗保健需求的提高也有关系。另外，医疗费用还表现为明显的季节趋势，在每年的3,4,10,11月出现高峰，这可能与该季节的气候环境有关，同时存在周期性，周期为S=12个月。

摸清医疗费用的增长趋势，建立预测模型可以为有关企业和部门制定措施提供依据，如医保部门制定财务规划、商业医疗保险制定赔付依据等。

4 参考文献

1中华人民共和国国家统计局.2010年第六次全国人口普查主要数据公报(第1号)〔R〕.2011.

2张 蔚，张彦奇，杨 旭.时间序列资料ARIMA季节模型及其应用〔J〕.第三军医大学学报，2002；4(8):955-7.

3陈 玲，徐慧兰.自回归求和移动平均模型在湖南省食物中毒预测中的应用〔J〕.中南大学学报(医学版)，2012；37(2):142-6.

4Brockwell PJ，Davis RA.Introduction to time series and forecasting〔M〕.New York：Springer Verlag,2002：179-219.

5Stadnytska T,Braun S，Werner J.Comparison of automated procedures for ARIMA model identification〔J〕.Behavior Res Meth,2008；40(1):250-62.

6Mehdi K,Mehdi B,Seyed RH.Combining seasonal ARIMA models with computational intelligence techniques for time series forecasting〔J〕.Soft Comput，2012；16:1091-105.

7宇传华.SPSS与统计分析〔M〕.北京: 电子工业出版社，2007：577-612.

8王 燕.应用时间序列分析〔M〕.北京: 中国人民大学出版社，2005：224-51.

9张 丽，闫世锋.Hoter-winters方法与ARIMA模型在中国航空旅客运输量测量中的比较研究〔J〕.上海工程技术大学学报，2006；20(3)：280-3.

10杜迅惠.医院出院人数的长期趋势及季节因素分析〔J〕.中国卫生统计，2009；26(2):175-6.