木荷胸径—树高生长相关模型研究

程玉娜，佘济云，孟 伟，邓必平，王威翔

(1.中南林业科技大学，湖南 长沙 410004； 2.浏阳市林业规划设计院，湖南 浏阳 410300)

木荷胸径—树高生长相关模型研究

程玉娜1，佘济云1，孟 伟1，邓必平2，王威翔1

(1.中南林业科技大学，湖南 长沙 410004； 2.浏阳市林业规划设计院，湖南 浏阳 410300)

在炎陵县青石岗林场，采用样地调查的方法测量木荷次生天然林树高、胸径；应用Excel软件绘制胸径与树高关系的散点图，选取比较适合散点分布趋势的线性方程、二次曲线、幂函数、对数函数4种生长模型，结合SPSS、Matlab软件对木荷胸径与树高的关系进行拟合。结果表明：在95%的置信区间内，对数函数的回归效果最显著，相关系数最大为0.992，残差平方和最小为18.689，正确率达 97.5%；在不考虑单个方程对整体的拟合效果时，用幂函数、对数函数、二次曲线函数3个模型的分段函数，更能准确地描述木荷的胸径树高生长特性，为最佳生长模拟模型。

木荷；生长模型；青石岗

木荷(SchimasuperbaGardn et Champ)又名荷树，为植物界被子植物门双子叶植物纲山茶科木荷属的常绿乔木。属于亚热带树种，嫩枝通常无毛，树冠广圆形，叶革质或薄革质、椭圆形。由于叶片为厚革质，耐火烧，萌芽力又强，故可用作防火带树种，是最为重要的防火阻燃用材树种，因此，良好的木荷林分结构是构筑安全的绿色屏障、防止减轻自然灾害的有效途径。

树高、胸径是衡量林分生长的2个较重要的指标[1]，学术界已经提出多种胸径—树高关系模型，例如：几何相似(geometry similarity)模型、弹性相似(elastic similarity) 模型、分形网络(fractal networks)模型[2-3]、及应力相似 ( stress similarity)模型[4]。树高与胸径的关系同时受到树木的立地条件、地下生物量等因素影响[5]。本文不考虑立地条件的不同，来拟合炎陵县青石岗林场木荷林胸径与树高间的相关性，在进行大量数据分析的基础上，通过选择较符合实际的4种模型，比较其拟合结果，最终选择出最优模型，为林业工作者提供一个科学、实用的测树方法，提高生产率和经济效益[6]。精确地定量化木荷树高为林业工作者编制各类经营数表，为实现森林资源的优化配置提供基础数据[7]，为科学地进行木荷林的经营管理决策提供参考。

1 研究区概况

炎陵县青石岗林场位于湖南省东南部，罗霄山脉中段和万洋山北段之西北坡、南岭山脉北麓，为南岭山地向湘中丘陵过渡的边缘地带，北纬26°48′、东经 113°77′，距省会城市长沙285 km。属亚热带季风性湿润气候，海拔900～1200 m，年均气温17.3 ℃，年均降水量1496.7 mm，年无霜期266 d以上，空气相对湿度较大，是名符其实的膏腴之地，适合种植农作物。全林场国有经营面积24754 hm2，有林地19664 hm2，有林地占林地面积79.44%。青石岗林场林业资源丰富，主要的优势树种有：木荷约占61%、杉木(Cunninghamialanceolata)约占10%、黄檀(Dalbergiahupeana)约占6.2%等。

2 研究方法

2.1 数据来源

运用典型选取及随机抽样相结合的方法，在生长良好、林相整齐的非林缘处木荷林中，选择立地条件相似、林相不同的、有代表性的标准样地9块(10 m×10 m)，每块样地分为4个5 m×5 m的小样地以方便调查，提高调查精度。利用罗盘仪精确地设置样地，使闭合差小于0.5%，利用测高器、围径尺、皮尺等测定并记录每块样地的名称、海拔、林龄、起源、经纬度、草本盖度、坡度、枯落物厚度、坡向、郁闭度以及植被群落等基本信息。在每个10 m×10 m样方内，起测胸径为2 cm，每木检尺胸径、树高、枝下高、冠幅、断梢等测树因子。

2.2 数据的处理

9块样地中共调查了323株胸径在2 cm以上的乔木，其中木荷有196株，占60.68%。剔除人为损害的、病虫害影响的、断梢的树木，本文选择160棵比较自然生长的木荷进行模型的研究与分析。利用Excel软件绘制以胸径为横坐标，树高为纵坐标的散点图，观察散点分布的形状与趋势，初步选定其可能符合散点分布趋势的4种模型[8-10]。再将其数值导入SPSS 17.0中进行拟合，用决定系数R2的大小来评价模型的拟合效果，其值越接近于1，说明回归方程拟合优度越好[1]；以F值的大小进行一致性检验，验证方程的显著性，最后用matlab软件进行残差分析。

2.3 模型的建立

3 结果与分析

3.1 模型拟合结果

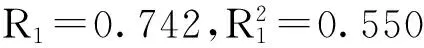
表1 线性回归模型系数表

由表2可知，二次曲线的模型方程为：H=3.572+0.397D-0.003D2，R2=0.63；方差分析表明，F=133.883

由表3可知，幂函数的模型方程为：H=2.384D0.487，R2=0.562；方差分析表明，F=202.445

表2 二次曲线回归模型系数表

表3 幂函数模型系数表

表4 对数函数变形模型系数表

图1 线性回归直线图图2 二次曲线拟合模型图

3.2 模型分析

3.2.1 单模型分析 根据“相关系数R(决定系数R2)越大、剩余平方或残差平方和越小，拟合效果越好”的原则[11]，分析说明各模型拟合结果；回归方程通过了F检验，只是表明回归方程是有效的，但不能保证数据拟合得效果很好，也不能排除由于意外原因而导致的实验数据不可靠，比如异常值的出现[1]。一般认为，如果一个模型的所有残差是在ei= 0 附近随机波动，并且是在一条幅度变化不大的带子以内，此时说明回归方程满足基本假设[13]。

图3 幂函数拟合图图4 对数函数变形拟合图图5 线性回归残差分析图图6 二次曲线残差分析图图7 幂函数残差分析图图8 对数函数变形模型残差图

线性模型：H=4.759+0.217D中，残差平方和RSS=504.327相对较大，说明方程回归效果不理想。F=193.283

3.2.2 模型对比分析 从表5可以看出，对数函数模型R=0.992比其他3个模型值都高，并且残差平方和RSS=18.689比其他3个模型都低，且一致性检验较为显著，说明对数函数对于描述树高生长趋势有显著意义[14]，可初步判断为最佳模型。

由于林木总处于不断的生长过程中，模型中的参数实际上是受树木生长因素变化而变化，因此模型参数往往都是随着时间的推移发生变化[15]。所以一个固定的模型远远达不到很好的模拟效果。在不考虑方程回归效果显著性时，最终可以得出适合炎陵县青石岗林场不同时段的木荷林胸径与树高关系的分段回归模型:

表5 拟合结果对比表

(1)

式中，H为树高(m)，D为胸径(cm)，M为一较大的常数。说明：胸径为3 cm处的模型节点是幂函数与对数函数的交点，40 cm是距离对数函数与二次曲线交点最近的一个实测点。又因实测胸径为离散点，因此模型的节点不一定就是原始数据的实测点，在此均取上开下闭的区间。

4 结论与讨论

由于青石岗林场中多数为次生林且被抚育过，因而调查样地中，过熟林极少。再加上木荷是极好的耐火树种，生长比较慢，因而在调查的样地中大部分的木荷为中龄林，成熟林及其他龄组的林分较少[18]，且胸径在40～55 cm之间出现了断层现象。由于实测的木荷胸径均为离散的点，而模型的表达式为连续函数，所以本文所模拟的胸径与树高的关系模型是否适应于由内推法算出的胸径在40～55 cm之间或由外推法得出的胸径在88 cm以上的木荷有待进一步验证。

[1]顾凤岐，王艳.基于红松胸径与树高相关模型的研究[J].森林工程，2013，29(4)：39-41.

[2]Brown J H，Gillooly J F，Allen A P，et al. Toward ametabolic theory of ecolog[J].Ecology，2004，85：1771-1789.

[3]Price C A，Oglk K，White E P，et al. Evaluating scalingmodels in biology using hierarchical Bayesian approaches[J].Ecology Letters，2009(12)：641-651.

[4]West G B，Brown J H，Enquist B J. A general model for thestructure and allometry of plant vascular systems[J].Nature，1999(400)：664-667.

[5]樊艳文，王襄平，曾令兵，等.北京栓皮栎林胸径——树高相关生长关系的分析[J].北京林业大学学报，2011，33(6)：146-150.

[6]李忠国，孙晓梅，陈东升，等.基于哑变量的日本落叶松生长模型研究[J].西北农林科技大学学报，2011，39(8)：69-74.

[7]魏晓慧，孙玉军，马炜.基于Richards方程的杉木树高生长模型[J].浙江农林大学学报，2012，29(5)：661-666.

[8]郑传英.四川桤木林分各主要生长因子间相关性研究[J].安徽农学通报，2010，16(17)：161-162.

[9]王晓林，郭斌.柞树树高与胸径相关关系的研究[J].森林工程，2012，28(6)：18-21.

[10]王利，丰震，白世红，等.麻栎树高与胸径相关关系的研究[J].山东林业科技，2005(4)：33-34.

[11]陈灿，洪伟，吴承祯，等.东南沿海湿地松防护林胸径树高关系研究[J].农学学报，2011，10(8)：35-41.

[12]罗建平.台湾峦大杉胸径与树高生长相关模型[J].林业科技，2013，38(1)：13-19.

[13]何晓群，刘文卿.应用回归分析[M].北京：中国人民大学出版社，2007.

[14]李春明，李利学.基于非线性混合模型的栓皮栎树高与胸径关系研究[J].北京林业大学学报，2009，31(4)：7-12.

[15]蒋艳，李玻，李任波.滇中云南松胸径和树高生长的GAM模型[J].林业调查规划，2009，34(6)：13-16.

[16]Mahmut D.Avsar，Veysel Ayyildiz.The Relationships between Diameter at Breast Height，Tree Height and Crown Diameter in Lebanon Cedars (Cedrus libani A.Rich.) of the Yavsan Mountain，Kahramanmaras，Turkey[J].Pakistan Journal of Biological Sciences，2005，8(9)：1228-1232.

[17]Liu Rentao，Bi Runcheng，Zhao Halin.Mathematical Simulations of the Relationship between Height and DBH of Juglans mandshurica Population in Taiyue Forest Region[J].Journal of Biomathematics，2008，23(3)：416-422.

[18]宋青，彭志，王金虎，等.苏州光福木荷林林分特征及经营对策[J].林业科技开发，2008，22(2)：30-33.

The Schima superba Diameter at Breast Height (DBH) and Height Relation Model Research

CHENG Yu-na1，SHE Ji-yun1，MENG Wei1，DENG Bi-ping2，WANG Wei-xiang1

(1.CentralSouthUniversityofForestryScienceandTechnology，Changsha410004，Hunan，China；2.ForestryPlanningandDesignInstituteofLiuyangCity，Liuyang410300，Hunan，China)

In the county of Yanling Qingshigang Forest Farm，adopt the method of sample plot survey to measure of theSchimasuperbaof secondary natural forest tree height，DBH.Applied of Excel software to draw a scatter plot of the relationship between the diameter at breast height and tree height.Selected linear equations，quadratic curve，power function and logarithmic function such 4 kinds of growth models.With SPSS，and Matlab softwares，it fitted theSchimasuperbaDBH and tree height relations.The results showed that：One was within the 95% confidence interval，the most significant regression effect was the logarithmic function，the maximum correlation coefficient was 0.992 and the minimum residual sum of squares was 18.689，the correct rate reached 97.5%.Another one was when no considering the effect of a single equation fitting，power function，logarithmic function and quadratic curve 3 models，it could more accurately describe the DBH，and tree height growth characteristics of Schima superba and were the best growth simulated model.

Schimasuperba；growth model；Qingshigang

10.13428/j.cnki.fjlk.2014.02.025

2013-08-27；

2013-09-29

国家林业局行业公益性项目(南方集体林区次生林抚育间伐与高效利用技术研究，201004032)

程玉娜(1988—)，女，河南开封人，中南林业科技大学在读硕士，从事林业信息工程研究。E-mail：cyn20080223@163.com。

佘济云，中南林业科技大学教授，博士生导师。从事森林经理和林业资源管理研究。E-mail：shejiyun@126.com。

S792.99；S758.62

A

1002-7351(2014)02-0109-06