甘蔗切割器系统轴裂纹识别分析
2014-09-11魏道高胡美玲区颖刚
魏道高,胡美玲,马 倩,区颖刚
(1合肥工业大学机械与汽车工程学院,安徽合肥 230009; 2华南农业大学南方农业机械与装备关键技术省部共建教育部重点实验室,广东广州 510642)
甘蔗切割器系统轴裂纹识别分析
魏道高1,胡美玲1,马 倩1,区颖刚2
(1合肥工业大学机械与汽车工程学院,安徽合肥 230009; 2华南农业大学南方农业机械与装备关键技术省部共建教育部重点实验室,广东广州 510642)
【目的】从甘蔗切割器系统多种非线性因素作用下的振动特性中获得识别轴裂纹的信息.【方法】将切割器简化成铅垂悬臂转子-支承系统,将斜裂纹设置在轴与盘身连接处附近,只考虑裂纹与切割力2种非线性因素建立了该系统的3自由度动力学方程.基于该模型,选用开斜裂纹刚度计算模型,对含斜裂纹的甘蔗切割器动力特性进行数值仿真.【结果和结论】当Ω=500 r·min-1系统在无裂纹而仅有非线性切割力作用下,横向振动出现了工频和组合频率响应;相同工况时,系统在含裂纹和非线性切割力双因素作用下,横向振动出现了工频和组合频率,但新增加了二倍频响应,且随裂纹深度增加二倍频响应幅值增加.由此可从2种非线性因素中获得识别轴裂纹信息.扭转振动则在有裂纹时比无裂纹情况下增加了工频成分.
甘蔗;切割器;斜裂纹;非线性切割力
切割器是甘蔗收获机重要的功能件,对其运动学及动力学特性在理论与试验方面都有广泛而深入的研究.Odouri等[1]建立了单圆盘切割器对甘蔗进行收割的运动学模型,且模拟了单圆盘旋转刀片切割边的运动轨迹变化情况.Kroes等[2]建立了双圆盘切割器的运动学模型,从理论上获得了满足刀盘与茎秆不接触、不产生漏割的条件,并对甘蔗直径、行宽和蔗秆基部倾角对收割机前进速度的影响进行了讨论.肖辉齐[3]基于甘蔗收获机单圆盘切割器和双圆盘切割器的运动学分析,分别建立了2种收获机圆盘转速、机器前进速度和刀片数量等参数匹配关系.刘庆庭[4]研究了根部切割器几何参数、运动参数和切割质量之间的关系,建立了运动学模型,获得切割器不漏割、不重切的机理;周仕城等[5]采用动力学仿真软件,建立甘蔗-切割器系统的动力学仿真模型,且进行了甘蔗切割物理试验验证,获得了一刀切断甘蔗时可靠性为95%的最佳切割力总区间.张正中等[6]通过研究甘蔗切割过程中受力、振动情况及其与蔗兜切割质量之间的关系,为切割器设计提供依据,同时建立了甘蔗切割模型,并对其进行了模态分析和动力学仿真.
切割器在工作过程中既受到马达驱动扭矩,同时又受到非线性切割力对刀盘轴的扭转阻力矩的双重扭矩作用.因此,刀盘轴就有可能产生斜裂纹.而地面行走的切割器既是功能件也是安全件,刀盘轴上裂纹是其安全工作的隐患,因此对轴上含斜裂纹切割器动力特性展开研究,为斜裂纹识别提供理论参考.从20世纪70年代起,国内外学者关于裂纹轴转子动力学特性及裂纹识别有了广泛的深入研究[7-10],但关于含裂纹的甘蔗刀轴动力特性研究很少.在以上研究基础上,本研究建立了考虑刀轴裂纹与刀盘切割力的切割器动力学系统的3自由度系统方程,分析在裂纹与切割力2种非线性因素共同作用下该系统的动力特性,从2种非线性因素中识别斜裂纹信息,为其安全设计提供理论参考.
1 含裂纹刀盘切割器系统动力学模型
1.1 含斜裂纹切割器系统力学模型
以国产某型单圆盘收获机为样机,对其切割器系统构建了力学模型,如图1所示.oxyz为该系统固定坐标系,其中xo'y为切割器水平切割面,x为工作时前进方向,刀盘顺时针旋转,y为切割甘蔗进动方向,z为刀轴铅垂安装方向.斜裂纹在刀轴与刀盘连接部位,d为刀轴直径,l为刀轴长度,R为刀盘半径,R1为切割器切割力工作点半径,F为切割力幅值,Fx、Fy为刀盘非线性切割力在x、y方向的分力.并且在构建力学模型时做了如下假设:假设转轴的支撑为刚性;忽略了刀盘倾角;假设转轴上的裂纹为45°开斜裂纹,转轴裂纹的位置在刀轴与刀盘连接部位;切割器工作过程中,假设刀盘旋转1周,4个刀片相继各切断1根甘蔗,且为一刀切断.
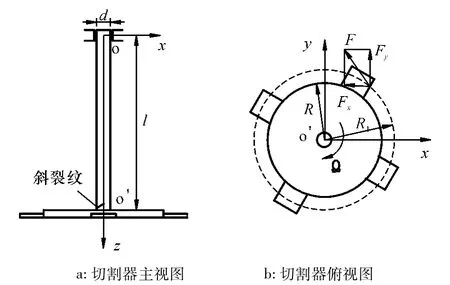
图1 含裂纹切割器力学模型Fig.1 The mechanical model of cutter with crack
1.2 切割器系统动力学方程
基于图1切割器-支撑系统模型,运用拉格朗日运动学方程建立该转子系统沿x、y方向进动和绕z方向旋转的运动微分方程组:
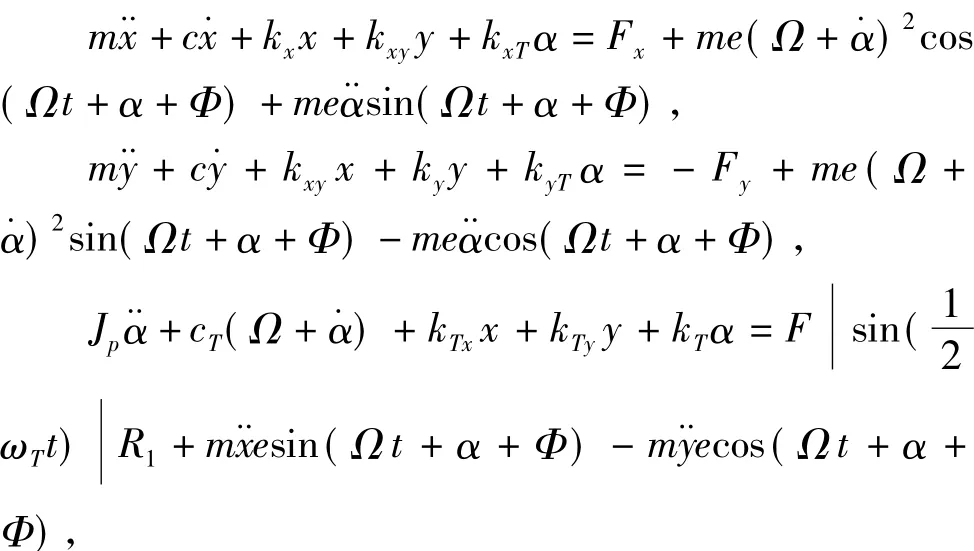

1.3 斜裂纹刚度计算方法选择
目前裂纹转子轴的刚度模型主要有2种:开裂纹模型和呼吸裂纹模型.本研究采用的切割器模型为直立转子,假定裂纹在转子运行过程中始终处于张开状态,为开裂纹.而对开裂纹轴刚度计算方法主要有当量法[8]、数值计算法[9]和 Dimarogonas方法[10-11].当量计算法比较粗糙;数值计算法需要花费大量的时间来编写程序,其结果的精度也受到具体数值算法的限制[12];Dimarogonas方法是一种用断裂力学中的应力强度因子和能量释放率来计算刚度的方法.与上述2种方法比较,有精度较高及较易实现的优点.本研究需了解切割器系统在x、y方向及绕z扭转方向的振动特性,而该方法可用来推导裂纹转子弯曲、扭转和纵向振动存在耦合时的刚度矩阵,从而方便地讨论裂纹转子的耦合振动问题[13],所以选用该方法来获得裂纹轴含各项耦合刚度的刚度矩阵.
本文根据附加柔度与能量释放率间的关系、能量释放率与应力强度因子间的关系寻求切割器轴含裂纹时的附加柔度.含裂纹时转轴的释放能为[14]:

式中,ϑ表示裂纹截面处积分单元长度;Y表示裂纹截面处纵坐标;KⅠ、KⅢ表示Ⅰ型(张开型)、Ⅲ型(撕裂型)裂纹模式的应力强度因子[12];E'=E/(1-μ2),E表示弹性模量;μ表示泊松比.
根据卡氏定理[15],附加局部柔度可表达为:

式中,qi表示qj各个方向上载荷i,j为附加局部柔度矩阵的行序号与列序号,q1、q2、q3分别为x、y及绕z扭转方向的载荷.
无裂纹时转轴柔度为:
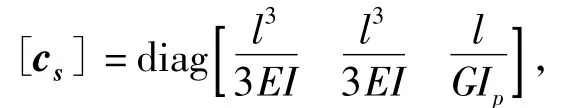
式中,I表示刀轴转动惯量;G表示剪切弹性模量;Ip表示刀轴极惯性矩;l为刀轴长度;E为弹性模量.
含裂纹轴的柔度为附加柔度加上无裂纹时转轴的柔度[12]为:
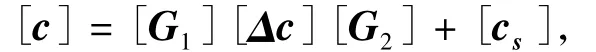
[G1]、[G2]表示转换矩阵;[Δc]为局部附加柔度矩阵.
旋转坐标系下裂纹轴的刚度矩阵[k]l即为柔度矩阵[c]的逆,[k]l=[c]-1.再进行转化得到固定坐标系下的刚度矩阵[k]g,[k]g=[H]-1[k]l[H],[H]表示坐标转换矩阵[16].
1.4 非线性切割力
本研究采用的甘蔗切割器切割力幅值为一刀切断甘蔗时的最大切割力[5].此切割力幅值为:
F=308.53-4.13θ-3.24β+0.091θ2+0.047β2+ 0.043γ2+0.107v2,
式中,θ表示刀片刃角;β表示刀片切割角;γ表示刀盘倾角;v表示刀盘线速度,v=(Ω+˙α)R1.切割力在x、y方向的分力为:

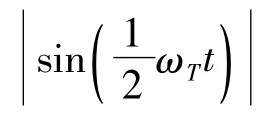
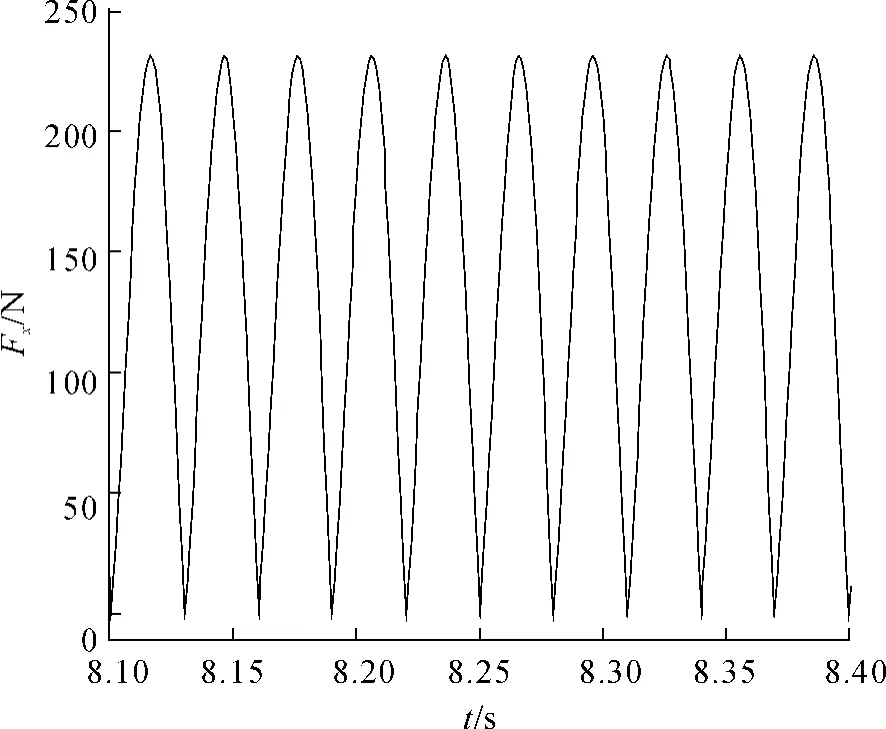
图2 切割力在x方向分力(Fx)随时间变化曲线Fig.2 The variational curve of the component of cutting force in the x direction(Fx)
2 含裂纹轴切割器动力特性与裂纹识别
以国产某型甘蔗收获机刀盘切割器作为样机,基于以上建立的数学模型,运用四-五阶龙格库塔法对该系统的动力特性进行数值计算.计算所需样机数据如表1所示,获得了仅有非线性切割力,以及在含裂纹和非线性切割力共同作用下,系统横向振动与扭转振动幅频特性,如图3、4、5和表2、3所示.

表1 计算切割器动力特性所需参数与其数值Tab.1 Parameters and values of calculating dynamic characteristics of the cutter

图3 仅有非线性切割力时系统x方向横向振动与绕z轴扭转振动幅频特性Fig.3 Amplitude-frequency characteristic of x direction vibration and z direction torsional vibration of the system with nonlinear cutting force only

图4 含裂纹且有非线性切割力时系统横向振动幅频特性Fig.4 Amplitude-frequency characteristic of transverse vibration of the system with both crack and nonlinear cutting force
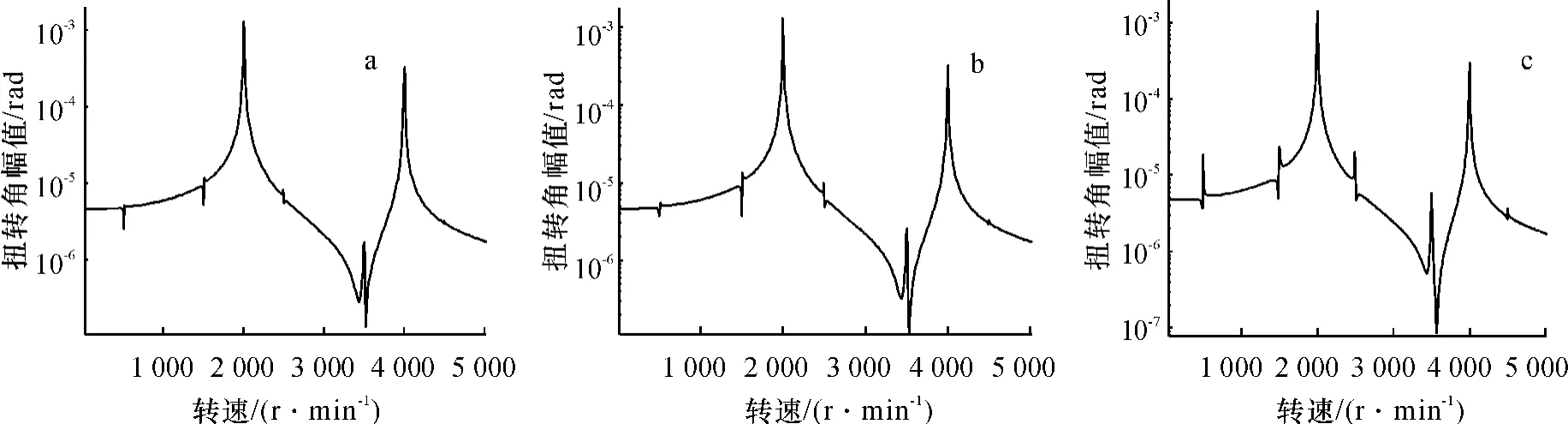
图5 含裂纹与非线性切割力时系统绕z轴扭转振动幅频特性Fig.5 Amplitude-frequency characteristic of z direction torsional vibration of the system with both crack and nonlinear cutting force
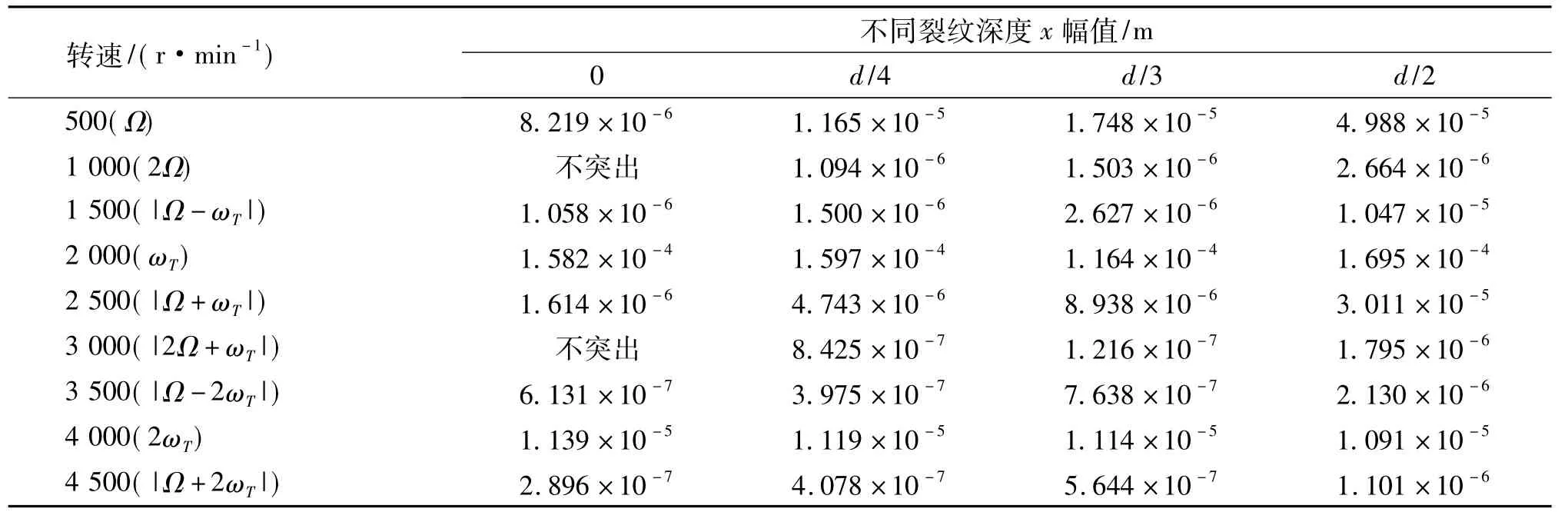
表2 随裂纹深度改变,x方向振动幅频特性的频率分布1)Tab.2 Frequency distribution of amplitude-frequency characteristics of x direction vibration with changes of the crack depth
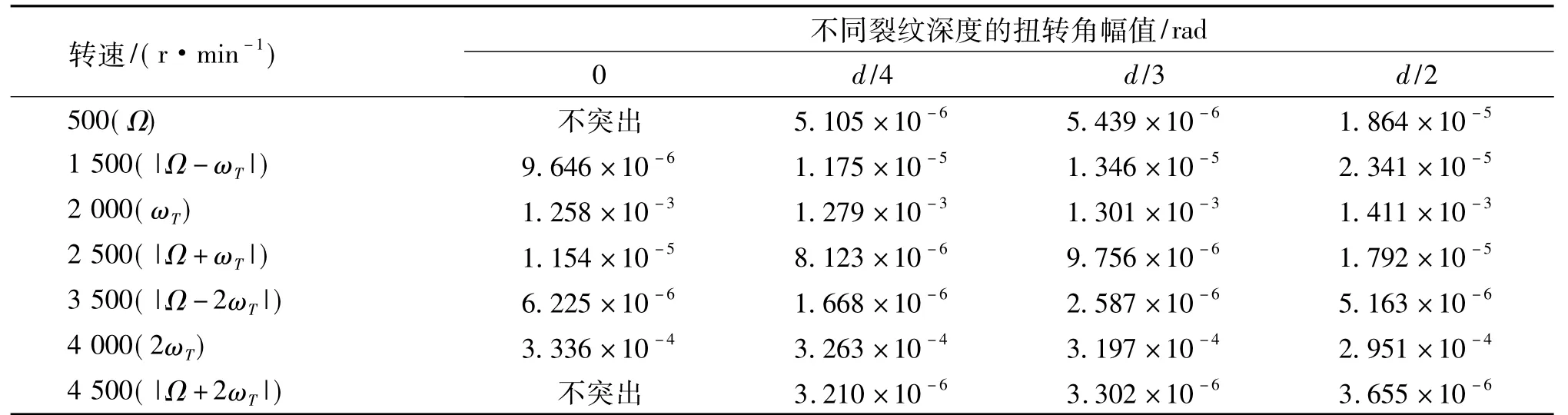
表3 随裂纹深度改变,绕z轴扭转振动幅频特性的频率分布1)Tab.3 Frequency distribution of amplitude-frequency characteristics of z direction torsional vibration with changes of the crack depth
综合甘蔗切割器刀轴无裂纹及含各种深度斜裂纹时x方向振动和绕z轴扭转振动幅频特性(图3);刀轴含裂纹与切割力F时刀盘在x方向振动幅频特性(图4);刀轴含裂纹与切割力F时刀盘绕z轴扭转振动幅频特性(图5);及表2、表3的归纳可知:
仅考虑非线性切割力时刀盘系统在x方向振动出现了组合频率;绕z轴的扭转振动出现了
考虑非线性切割力和裂纹时:刀盘系统在x方向振动出现了 Ω、2Ω、组合频率,比无裂纹时增加的频率成分有而绕z轴的扭转振动出现了,比无裂纹时增加的频率成分有Ω外,随着裂纹深度增加系统横向振动频率幅值除2ωT对应幅值外,都逐渐增大;扭转振动幅值除2ωT对应幅值外,也都逐渐增大.仅有非线性切割力作用时不会产生二倍频响应,二倍频分量的出现和增加趋势是裂纹存在和扩展的重要标志[17],因此,可以用二倍频来识别切割器刀轴的裂纹信息.
3 结论
本研究考虑刀轴斜裂纹和非线性切割力建立了切割器转子系统3自由度动力学方程.
仅考虑切割器非线性力系统横向频率特性表现为工频和组合频率响应;考虑2种非线性因素时系统横向频率特性表现为工频、组合频率和新增的二倍频响,且2Ω的幅值随裂纹深度增加而增大,由此可见,可以通过横向振动二倍频识别刀盘轴斜裂纹的存在.
在考虑以上2种非线性因素时,随着斜裂纹深度增加系统横向振动与扭转振动多频响应幅值都有增长趋势.扭振幅值的增加进一步导致斜裂纹扩展直至轴的疲劳失效.
从裂纹与切割力2种非线性因素识别出刀轴斜裂纹信息,为刀盘切割器系统安全设计提供理论参考.
[1] ODOURI M F,GUPTA C P.Design of the revolving knife:Type sugarcane basecutter[J].ASABE,1992,35 (6):1747-1752.
[2] KROES S,HARRIS H D.A kinematic model of dual basecutter of a sugar cane harvester[J].J Agr Eng Res,1995(62):163-172.
[3] 肖辉齐.甘蔗收割机切割器主要参数的确定[J].农机情报资料,1979(8):25-28.
[4] 刘庆庭.甘蔗切割机理[D].广州:华南农业大学,2004:6.
[5] 周仕城,杨望,杨坚,等.一刀切断甘蔗动力学仿真试验[J].农业机械学报,2011,42(1):68-73.
[6] 张正中,梁式,吕焕培,等.基于ANSYS/LS-DYNA的甘蔗切割动力学仿真分析[J].农机化研究,2010,32 (1):64-67.
[7] SUNDERMEYER J N,WEAVER R L.On crack identification and characterization in a beam by non-linear vibration analysis[J].J Sound Vib,1995,183(5):857-871.
[8] 陈真勇.转子系统故障辨识理论、方法和实验研究[D].北京:清华大学,2003.
[9] 朱厚军.裂纹轴刚度模型及裂纹转子动力特性的研究[D].上海:上海交通大学,2002.
[10]DIMAROGONAS A D.Vibration of cracked structures:A state of the art review[J].Eng Fract Mech,1996,55 (5):831-875.
[11]DARPE A K.Coupled vibrations of a rotor with slant crack[J].J Sound Vib,2007,305:172-193.
[12]林言丽.斜裂纹转子系统的动力学特性[D].北京:清华大学,2009.
[13]张文著.转子动力学理论基础[M].北京:科学出版社,1990:12.
[14]褚武扬.断裂力学基础[M].北京:科学出版社,1979:10.
[15]刘鸿文.材料力学[M].北京:高等教育出版社,2004:1.
[16]林言丽,褚福磊,郝如江.开斜裂纹转子的动力特性[J].振动与冲击,2008,27(1):25-29.
[17]张正松,傅尚新,冯冠平,等.旋转机械振动监测及故障诊断[M].北京:机械工业出版社,1991:351-352.
【责任编辑 霍 欢】
An analysis of crack identification in the shaft of sugarcane cutter system
WEI Daogao1,HU Meiling1,MA Qian1,OU Yinggang2
(1 School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009,China; 2 Key Laboratory of Key Technology on Agricultural Machine and Equipment,Ministry of Education,South China Agricultural University,Guangzhou 510642,China)
【Objective】To get identification information of crack on the shaft from vibration characteristics of the system under the condition of various nonlinear factors.【Method】The cutter was simplified to a vertical over-hung rotor-bearing system,and the slant crack was set near the junction between the shaft and the disk,taking into consideration two nonlinear factors.The slant crack and the nonlinear cutting force,three degrees of freedom dynamic equations of the system were founded.Based on this model,a stiffness calculation model of opening slant crack was chosen.The dynamic characteristics of the slant cracked cutter were investigated by numerical simulation.【Result and conclusion】The results showed that when Ω=500 r·min-1system was only under the condition of nonlinear cutting force without crack,working frequency and combined frequencies appeared in frequency responses of transverse vibration.In the same working condition,when the system was under the condition of both crack and nonlinear cutting force,the system had working frequency,combined frequencies and also a newly added second harmonic frequency which were frequency responses.In addition,with the increase of the crack depth,the amplitude of the second harmonic frequency was also increasing.Therefore,the identification signal of crack can be attained from two nonlinear factors.Besides,in torsional vibration,working frequency newly appeared because of the crack.
sugarcane;cutter;slant crack;nonlinear cutting force
S225
A
1001-411X(2014)03-0105-06
2013-04-08 优先出版时间:2014-03-31
优先出版网址:http:∥www.cnki.net/kcms/doi/10.7671/j.issn.1001-411X.2014.03.019.html
魏道高(1965—),男,副教授,博士,E-mail:weidaogao@hfut.edu.cn
省部共建教育部重点实验室开放基金资助项目(KF200707);国家自然科学基金(51050002、51375130)
魏道高,胡美玲,马 倩,等.甘蔗切割器系统轴裂纹识别分析[J].华南农业大学学报,2014,35(3):105-110.
