大气校正模型对阔叶林叶面积指数遥感估算的影响
2014-09-11顾哲衍张金池
顾哲衍,张金池,林 杰,韩 诚,刘 鑫
(南京林业大学森林资源与环境学院,江苏南京 210037)
大气校正模型对阔叶林叶面积指数遥感估算的影响
顾哲衍,张金池,林 杰,韩 诚,刘 鑫
(南京林业大学森林资源与环境学院,江苏南京 210037)
【目的】为利用遥感技术定量提取区域尺度的阔叶林叶面积指数前的大气校正模型选择提供科学依据.【方法】分别利用6S模型、FLAASH模型和ATCOR2模型对Landsat 8 OLI影像进行了大气校正,分析了3种模型下的阔叶林叶面积指数(LAI)与多种植被指数(VI)相关性,建立了LAI-VI的线性和非线性的回归模型,最后通过验证数据组LAI预测值(Y)与LAI实测值(X)的均方根误差(RMSE)及线性相关性大小对阔叶林LAI遥感估算结果进行了精度对比.【结果和结论】ATCOR2模型不适于阔叶林LAI-VI的回归建模;除比值植被指数(RVI)外,FLAASH模型与6S模型下的阔叶林LAI与增强型植被指数(EVI)、修正土壤调节植被指数(MSAVI)有较好的相关性,其中FLAASH模型下的阔叶林LAI-MSAVI幂函数模型拟合优度最佳;FLAASH模型的阔叶林LAI估算精度优于6S模型;借助遥感技术定量提取植被生理参数时,应慎重选择适宜的大气校正模型.
遥感;叶面积指数;大气校正
叶面积指数(Leaf area index,LAI)是定量分析地球生态系统能量交换特性的一个重要结构变量[1],不仅是表征植物冠层结构和植物群落生产力的基本指标,亦与众多生态过程(蒸腾、光合、呼吸、元素循环等)密切相关,直接影响植物对光能的截获和利用,间接影响冠层阻抗,同时作为决定地表反射率的重要参数对地表和大气间的相互作用有着重要影响[2].地面测量只能获得点状或线状的LAI数据,难以反映LAI的空间变异性,定量遥感技术作为反演陆面参数的一种重要方法,为实时获取大范围LAI提供了高效途径[3-4].
电磁波在太阳-目标物-卫星之间的传输过程极其复杂,不仅与光照条件、传感器的探测光谱响应、地表起伏等有关,更受到吸收、散射等大气作用的影响,必然导致辐射传输失真,严重降低LAI的反演精度.因而在定量反演LAI前,必须进行大气校正.大气校正模型可分为3类:基于辐射传输机理的校正模型(如6S模型、ATCOR2模型)、基于影像特征的校正模型(如表观反射率模型、Gilabert模型等)和基于地面定标参数的校正模型[5].其中,基于辐射传输机理的校正模型物理意义最明确、精度最高,应为大气校正未来的发展趋势[6-7].不同的大气校正模型获得的植被反射光谱信号不同,故选择适宜的大气校正模型对LAI的遥感反演具有重要意义[8].目前,对于大气校正模型的研究或集中于模型自身算法[9-11],或集中于模型算法间的横向比较[12-13],而对于不同大气校正模型在具体某一陆面参数反演中的适用性研究却鲜有报道.
鉴于此,本文选取基于辐射传输机理的校正模型中具有代表性的6S模型、FLAASH模型和ATCOR2模型分别对OLI(Operational land imager)影像进行大气校正,建立LAI与阔叶林植被指数(Vegetation Index,VI)的统计回归模型,探究3种大气校正模型对阔叶林LAI遥感反演精度的影响,旨在为大面积反演阔叶林LAI前的大气校正模型选择提供借鉴和参考.
1 材料与方法
1.1 研究地区概况
江宁区位于江苏省南京市南部,介于东经118° 31'~119°04',北纬30°38'~32°13'之间,总面积1 500多km2.常态地貌有低山、丘陵、岗地、平原和盆地,海拔1~371 m,境内河道主要有长江和秦淮河两大水系.气候属北亚热带季风湿润气候区,年平均气温15.5℃,年均无霜期224 d,年均降水量1 012 mm,年均日照2 148.3 h.全区有木本及药用植物1 000余种,较珍贵的有银杏Ginkgo biloba、雪松Cedrus deodara、明党参Changium smyrnioides、夏枯草Prunella vulgaris等.
1.2 数据来源及预处理
研究数据由Landsat 8 OLI多光谱影像数据和阔叶林LAI野外实测数据组成.OLI数据由美国地质勘探局(USGS)提供,轨道号Path 120/Row 38,成像日期2013年8月 13日,探测波普长度为 0.433~1.390 μm,已经过系统级的辐射和几何纠正.OLI涵盖Landsat 7 ETM+的所有波段,为了避免大气吸收特征,OLI对波段进行了重新调整,比较大的调整是OLI Band 5(0.845~0.885 μm),排除了0.825 μm处水汽吸收特征;OLI全色波段Band 8波段宽度较窄,有利于更好地区分地表有植被和无植被特征.以江宁区1∶5万地形图为标准底图,采用二次多项式拟合法,对OLI影像进行了几何精纠正,误差控制在0.5个像元内.阔叶林LAI野外实测数据由美国LICOR公司的LAI-2200冠层分析仪测得,时间为2013年8月下旬至9月初,样点数48个,其中8月下旬34个,9月初14个,主要分布在铜山、将军山、方山等地.研究区内分布广面积大的为毛竹Phyllostachys heterocycla纯林、麻栎Quercus acutissima纯林和阔叶混交林,为采样重点林分,样点数较多,分别为19、7和11个,其他林分如黄果朴Celiis labilis纯林、香樟Cinnamomum camphora纯林、构树Broussonetia papyrifera纯林以及广玉兰Megnolia grandiflora和三角枫Acer buergerianum等面积相对较小,LAI梯度明显,各林分设置1~4个典型样点,为表述简洁,本文将此类纯林统称为其他林分.考虑到OLI影像30 m的空间分辨率,采样间距均大于30 m,每个样点均由GARMIN手持GPS接收机定位,坐标系为WGS-84.各样点重复测量2次,取均值作为结果.
1.3 基于辐射传输机理的大气校正模型
1.3.1 6S(Second simulation of satellite signal in the solar spectrum)模型 6S模型将气体分子(水汽、CO2、O3等)的吸收、散射与气溶胶的散射一并予以考虑,采用最新近似(State of the art)和连续散射SOS (Successive orders of scattering)算法来求解辐射传输方程,提高了对瑞利散射和气溶胶散射的计算精度.在处理不均一目标时,考虑了一定半径之内的地物反射及该范围之外的背景干扰.同时,解决了地表双向反射分布函数(BDRF)与大气环境相互耦合的问题[14-15].其基本计算公式为:
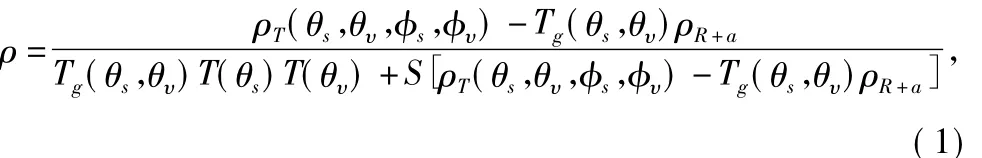
式(1)中:ρ为地表反射率,ρT(θs,θυ,φs,φυ)为大气上界反射率,Tg(θs,θυ)为太阳-目标物大气路径透过率,ρR+a为气体分子散射和气溶胶散射所构成的路径辐射反射率,T(θs)为大气透过率,T(θυ)为传感器-目标物大气路径透过率,θs为太阳天顶角,θυ为传感器天顶角,φs为太阳方位角,φυ为传感器方位角,S为大气半球反射率.
1.3.2 FLAASH(Fast line-of-sight atmospheric analysis of spectral hypercubes)模型 FLAASH实际是MODTRAN4+辐射传输模型的一种改进型,适用于可见光、近红外到短波红外范围内的光谱,为反演高光谱影像反射率的首选模型,能有效消除大部分大气和光照等因素对地物反射的影响,获得较为准确的地物反射率、地表温度等真实物理参数[16],对太阳光谱范围的限制和近似标准的朗伯体平面的假设是该算法的核心部分[17].其基本计算公式为:

式(2)中:L为传感器处单个像元的总辐射,ρ为像元地表反射率,ρe为该像元和其周边区域的平均地表反射率,Sf为大气向下的反照率,La为大气程辐射,A、B是基于大气透过率和几何条件的系数.
1.3.3 ATCOR2(A spatially adaptive fast atmosphere correction-2)模型 ATCOR2是一种针对太阳光谱和热光谱范围的快速大气纠正模型,对于大气均匀分布的雾霾和其他气体都具有独特的效果.大气状况通过一个查证表来描述.其算法可分为3步,①忽略邻近效应计算地表反射率;②计算每个像元邻近范围内的平均反射率,邻近效应的去除由一个N×N的低通滤波器来实现,N值大小取决于大气参数、光谱波段等;③在计算背景反射率(ρr)为0.15时,包含球形反射率对全球通量(碳通量,热通量等)的影响,模型的最后一步通过平均反射率与ρr的差值对其进行了校正[18].其第①和②步的计算公式为:
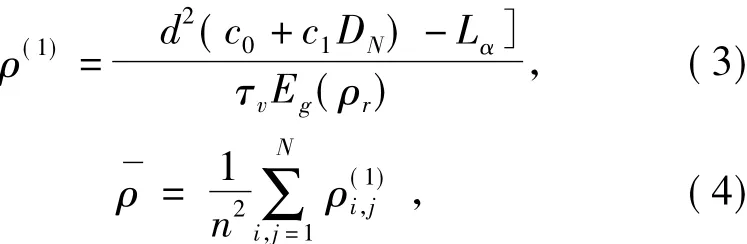
式(3)中:ρ(1)为地表反射率;d为日地距离;c0为传感器辐射响应度;c1为传感器偏移值;Lα为大气程辐射;DN为影像灰度值;τv为地表到传感器的总透过率;Eg为地面辐照度.式(4)中为像元邻近范围平均反射率;N为低通滤波器大小;为像元(i,j)的地表反射率;n为影像像元总数.
1.4 基于统计模型的LAI遥感反演
基于统计模型的LAI遥感反演法具有参数少、计算效率高、容易实现等优点,常被用于提取中小区域尺度的LAI,而植被指数与LAI之间的密切关系则是这一方法的理论基础[19].植被指数种类较多,本文在参考前人工作的基础上[3,15,19],考虑土壤、大气背景对LAI反演的影响,选取比值植被指数(RVI)、归一化植被指数(NDVI)、增强型植被指数(EVI)和修正土壤调节植被指数(MSAVI)与实测LAI建立统计回归模型.4类植被指数提取公式如下[15]:
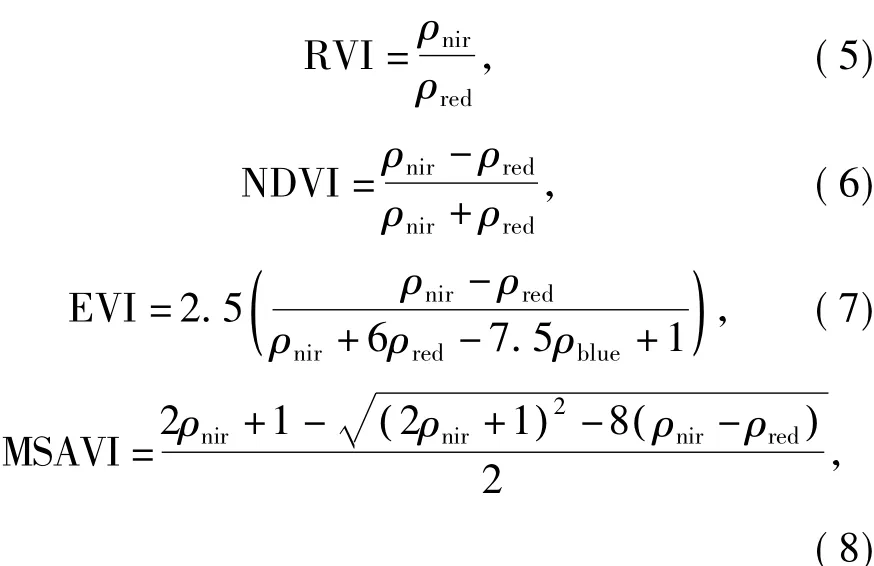
公式(5)~(8)中,ρnir、ρred和ρblue分别为大气校正后的近红外、红光和蓝光地表反射率.
2 结果与分析
2.1 不同林分类型的LAI统计特征分析
LAI定量描述了植物群体空间水平上叶子生长状况(数量、密度等)的变化,不同阔叶林类型的LAI有一定差异.由图1可以看出,毛竹林的LAI平均值最大,其方差亦高于麻栎林和阔叶混交林.毛竹生长快,成材早,是典型的速生树种,林分易形成水平和垂直郁闭,LAI均值偏大,研究区内的毛竹均为人工林,间伐抚育等人为干扰作用强烈,LAI波动较强,因而其方差亦较大.阔叶混交林多为天然林,麻栎林主要分布在山顶,二者受外界干扰作用较少,LAI梯度变化不明显.其他林分数据组包含的树种多,LAI梯度变化明显,方差大,且树种多为高大乔木,如黄果朴、香樟等,复层枝叶比重大,叶片总量多,LAI平均值亦大.
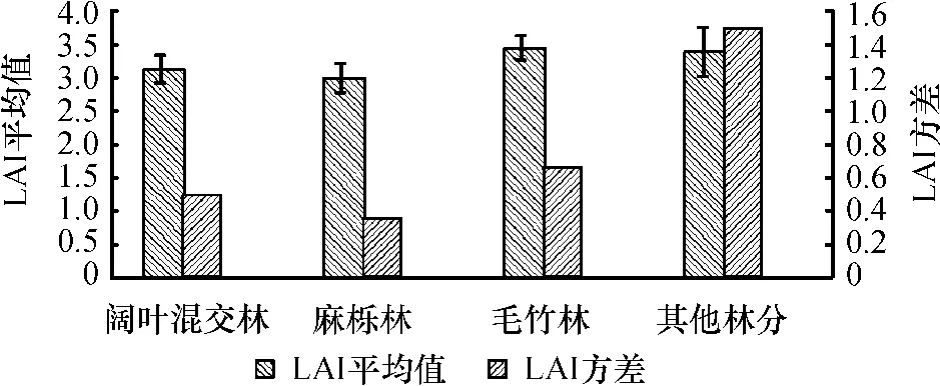
图1 不同林分类型的LAI平均值和方差Fig.1 Mean value and variance of vegetation indices by forest types
2.2 LAI-VI统计回归模型的建立与相关性分析
LAI与VI之间的相关性分析是确定能否应用遥感技术进行大区域叶面积指数反演的前提.本文选取与OLI影像成像日期较为接近的8月下旬实测的34个样本点作为LAI-VI建模数据组,以9月初实测的14个样本点作为模型验证数据组,并分别与LAI进行Pearson相关性分析(表1).显然,2种统计方式下的6S与FLAASH模型的LAI-VI相关性远高于ATCOR2模型.ATCOR2是二维的大气校正模型,计算简单,通常要求大气均匀分布,在去除大气影响时,做了较多的影像增强处理,导致影像的真实性减弱,只适合在小尺度局部区域应用.混合像元和邻近像元等因素会严重影响其校正精度,其算法中的一般近邻效应的有效范围约500~1 000 m,但若相邻区反射率有很大差异时,近邻效应的影响范围可扩大至2 000 m以上[20].2种统计方式下的FLAASH模型和6S模型的LAI-VI相关性普遍通过0.05置信水平检验.建模数据组中,LAI-RVI相关性最低,LAIEVI与LAI-MSAVI的相关性均通过0.01置信水平检验,达到了极显著水平,都可作为建模首选植被指数.LAI-NDVI相关性高于LAI-RVI,但尚未达到极显著水平.同时注意到,虽然FLAASH模型的LAI-VI相关性略优于6S模型,但已非常接近,因而仍需对这2种大气校正模型下的LAI反演结果进行进一步的精度验证.鉴于上述,本文仅对FLAASH模型与6S模型下的LAI-EVI/LAI-MSAVI进行建模与验证.
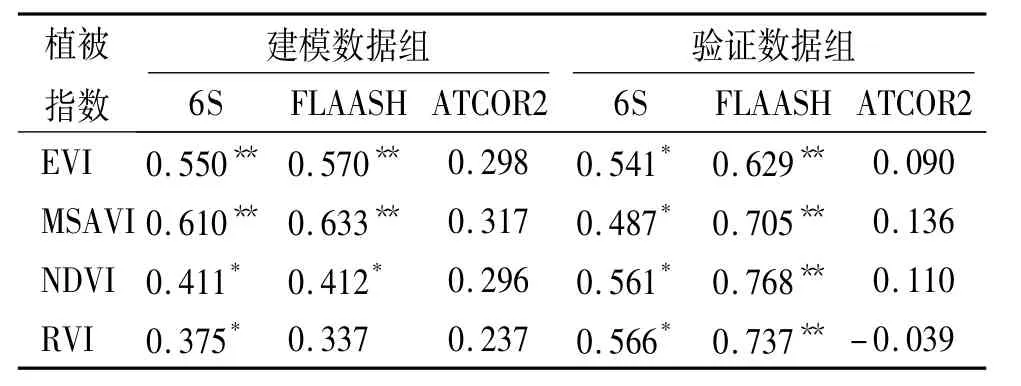
表1 3种模型在2种统计方式下所得Pearson相关系数比较1)Tab.1 Pearson correlation coefficients comparison using two statistical methods under three models
2.3 LAI-VI统计回归模型的建立及精度验证
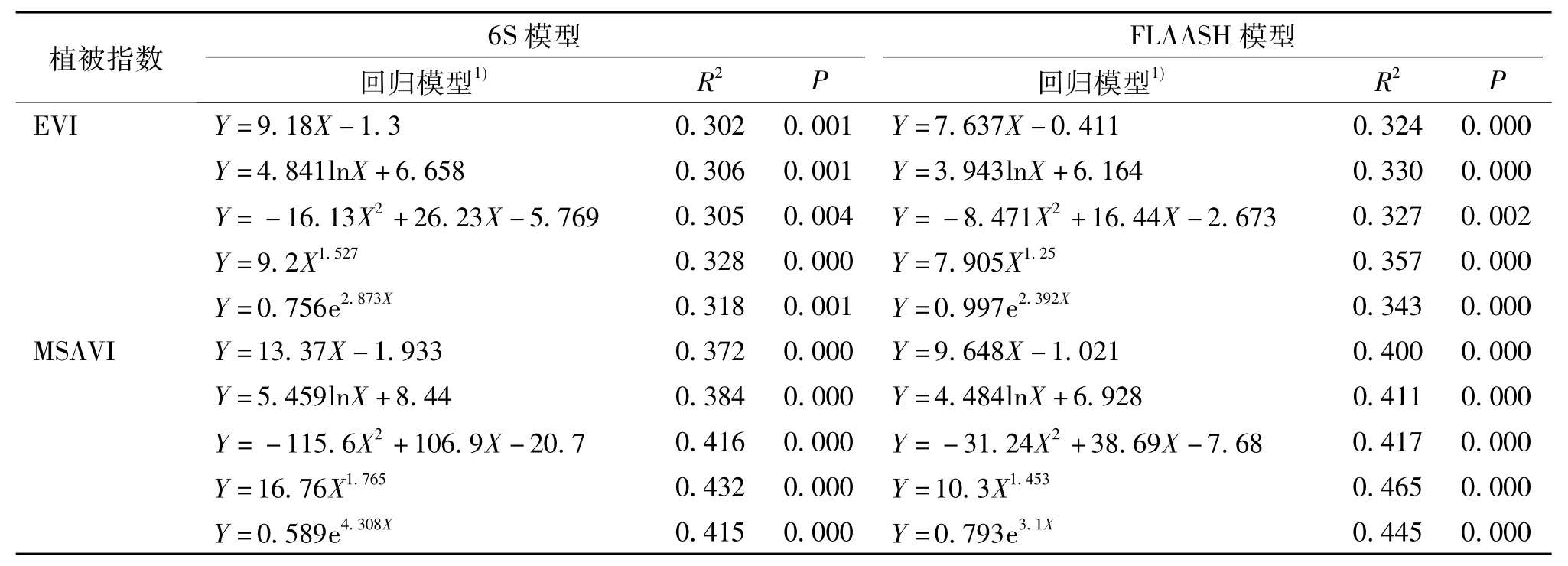
表2 2种大气校正模型下的叶面积估算模型Tab.2 LAI estimation model under two atmospheric correction models
2.3.1 LAI-VI统计回归模型的建立 利用建模数据组数据建立基于像元尺度的LAI-VI回归模型,如:线性回归模型、指数模型、二次多项式模型等,找出最合理的回归模型,回归模型见表2.2种大气校正模型下,LAI-VI回归方程的显著性水平(P)均小于0.05,即具有统计学意义,回归方程均是成立的.
由表2可知:①从植被指数角度看,2种大气校正模型下的LAI-MSAVI回归模型的拟合优度R2值总体高于LAI-EVI.研究区植被分布不均,种类繁多,在OLI影像30 m的分辨率下,必然产生大量植被-土壤混合像元.MSAVI是土壤调节植被指数(SAVI)的改进型,建立了简单的植被-土壤系统模型,相比SAVI而言,更加充分地考虑了土壤因素的变动.②从大气校正模型角度看,FLAASH模型下的LAI-VI的R2值整体高于6S模型.FLAASH模型通过计算影像上的黑暗像元来反演气溶胶厚度,6S模型则是对各像元逐一求算,范文义等[7]认为对于ETM+传感器而言,FLAASH模型在还原植被真实波普信息时有所欠缺,但6S模型对于OLI影像光谱范围内的滤光函数难以界定,采用光谱上下限近似求解,在很大程度上影响了6S模型对OLI影像的校正精度.注意到,2种模型下,拟合优度最高的均是LAI-MSAVI幂函数方程(6S模型R2=0.432,FLAASH模型R2= 0.465).6S模型与FLAASH模型都遵循辐射传输机理,辐射传输方程定量考虑了地形、地球曲率、大气密度、气压等对光辐射的影响,模型参变量具有部分共性,且研究区大气模式相对固定,因而2种模型下LAI-VI总体呈相似趋势.
2.3.2 精度验证 鉴于回归模型的拟合优度R2值为参与建模数据内部的拟合优度检验值,为了能够更客观地评价各模型下的LAI反演精度,本文利用未参与建模的验证数据组带入2种大气校正模型下最理想的LAI-MSAVI幂函数模型,并计算LAI实测值和预测值的均方根误差(RMSE)及线性相关性大小(R2),以内外结合的方式来交叉检验反演精度.RMSE计算公式如式(9)所示,其值大小仅表示预测值接近真实值的程度,值愈小则表示预测效果愈好.
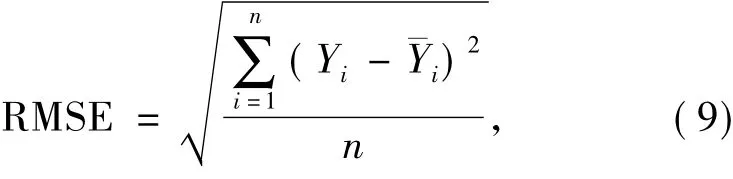
式中:Yi为LAI实测值;为LAI模拟值,n为验证数据组样本自由度.
由表3可知,2种大气模型下的LAI实测值与LAI预测值的线性相关性R2值均较高,RMSE相近,说明二者皆可用于LAI反演.FLAASH模型下的R2值大于6S模型,RMSE小于6S模型,基于OLI影像的 FLAASH模型反演 LAI精度略高于 FLAASH模型.

表3 不同大气校正模型下的RMSE和R2值比较Tab.3 Comparison of RMSE and R2under two atmospheric correction models
3 讨论与结论
本文利用LAI与植被指数之间的相关关系,分析比较了基于辐射传输机理的3种大气校正模型(6S、FLAASH和ATCOR2)对阔叶林LAI反演精度的影响.ATCOR2模型对大气状况具有理想化的假设,要求大气均匀分布,校正运算时,对影像进行多次的增强和拉伸,校正后的影像存在较严重的辐射失真现象,导致LAI与植被指数的相关性过低,难以用于LAI遥感定量估算.王建等[20]详细解析了ATCOR2模型算法,认为其着重于改善影像目视质量,适合在小尺度局部区域的遥感影像中应用,而在较为精确的定量遥感应用中,则需考虑应用数字地形模型(Digital terrain model,DEM)对图像进行预处理,以消除地形对地表反射特性的影响,这与本文的分析结果是一致的.FLAASH模型与6S模型下,除RVI外,LAI-VI回归模型相关性整体良好.虽然6S模型较FLAASH模型而言,在计算气溶胶效应时更为准确,但对于OLI影像的光谱滤光函数没有精确的界定,校正后的影像植被指数与 LAI相关性不如FLAASH模型.
本研究区域属城乡结合地区,建设用地和耕地居多,林地覆盖度不高,地表红光反射作用较强,RVI对LAI的敏感性降低.MSAVI综合考虑了植被-大气和土壤-大气的交互作用,因而2种大气校正模型下的LAI-MSAVI幂函数拟合优度最佳,适于研究区的LAI反演.
经过对FLAASH模型和6S模型的LAI-MSAVI幂函数模型的反演结果的RMSE和线性相关性的比较,FLAASH模型更适于大面积的LAI遥感估算.由于研究区域地形不复杂,因此在运用FLAASH模型与6S模型时,本文视地表为均一的朗伯面,未考虑地表双向反射效应,这在某种程度上影响了LAI遥感估算精度.今后工作中,应运用地表双向反射效应对大气校正结果进行订正,从而提高LAI的估算精度.
[1] 李开丽,蒋建军,茅荣正,等.植被叶面积指数遥感监测模型[J].生态学报,2005,25(6):1491-1496.
[2] 邵璞,曾晓东.CLM3.0-DGVM中植物叶面积指数与气候因子的时空关系[J].生态学报,2011,31(16):4725-4731.
[3] 林文鹏,赵敏,张翼飞,等.基于SPOT 5遥感影像的城市森林叶面积指数反演[J].测绘科学,2008,33(2):57-59.
[4] CHEN J M,PAVLIC G,BROWN L,et al.Derivation and validation of Canada wide coarse resolution leaf area index maps using high-resolution satellite imagery and ground measurements[J].Remote Sens Environ,2001 (80):11-20.
[5] 陈新芳,陈镜明,安树青,等.不同大气校正方法对森林叶面积指数遥感估算影响的比较[J].生态学杂志,2006,25(7):769-773.
[6] 王钊.6S辐射模型算法解析及在MODIS大气校正中的应用[J].陕西气象,2006(5):34-37.
[7] 范文义,孙晓芳,王岩,等.基于两种辐射传输模型的遥感数据大气校正及结果对比分析[J].东北林业大学学报,2009,34(7):121-124.
[8] 宋巍巍,管东生.五种TM影像大气校正模型在植被遥感中的应用[J].应用生态学报,2008,19(4):769-774.
[9] 郑伟,曾志远.遥感图像大气校正的黑暗像元法[J].国土资源遥感,2005(1):8-11.
[10]CHEN Jun,QUAN Wenting,ZHANG Minwei,et al.A simple atmospheric correction algorithm for modis in shallow turbid waters:A case study in Taihu Lake[J].Sel Top Appl Earth Observ Remote Sens,2013,6(4):1825-1833.
[11]REMMEL T K,MITCHELL S W.The importance of accurate visibility parameterization during atmospheric correction:impact on boreal forest classification[J].Int J Remote Sens,2013,34(14):5213-5227.
[12]张婷媛,林文鹏,陈家治,等.基于FLAASH和6S模型的Spot 5大气校正比较研究[J].光电子·激光,2009,20(11):1471-1473.
[13] 杨杭,张霞,帅通,等.OMIS-Ⅱ图像大气校正之FLAASH法与经验线性法的比较[J].测绘通报,2010 (8):4-6.
[14]买买提依明·买买提,塔西甫拉提·特依拜,买买提沙吾提,等.基于6S模型的遥感数据大气校正应用研究[J].水土保持研究,2011,18(3):15-18.
[15]林杰.基于植被结构特征的土壤侵蚀遥感定量反演[D].南京:南京林业大学,2011.
[16]赵国祥,苗放.高光谱影像FLAASH大气校正模型参数影响与评价——以西藏山南为例[J].科技资讯,2012 (34):6-7.
[17]郭云开,曾繁.基于FLAASH与QUAC模型的SPOT 5影像大气校正比较[J].测绘通报,2012(11):21-23,41.
[18]程亮,马友华,黄艳艳,等.ENVI FLAASH和ERDAS ATCOR2的大气校正对比研究[J].农业网络信息,2011(12):17-20.
[19]朱高龙,居为民,范文义,等.帽儿山地区森林冠层叶面积指数的地面观测与遥感反演[J].应用生态学报,2010,21(8):2117-2124.
[20]王建,潘竟虎,王丽红.基于遥感卫星图像的ATCOR2快速大气纠正模型及应用[J].遥感技术与应用,2002,17(4):193-197.
【责任编辑 李晓卉】
Effects of atmospheric correction on remote sensing estimation of LAI of broadleaved forest
GU Zheyan,ZHANG Jinchi,LIN Jie,HAN Cheng,LIU Xin
(College of Forest and Environment,Nanjing Forestry University,Nanjing 210037,China)
【Objective】This study aimed to provide a scientific basis for selecting the atmospheric correction model prior to the quantitative extraction of leaf area index of broadleaved forest at a regional scale using remote sensing.【Method】6S model,FLAASH model,and ATCOR2 model were used respectively on Landsat 8 OLI image for the atmospheric correction to analyze the correlation of these three kinds of leaf area index(LAI)of broadleaved forest and a variety of vegetation index(VI),establishing the linear and nonlinear regression model of LAI-VI.The root mean square error and correlation of validation data set of LAI predicted value(Y)and the LAI measured values(X)were calculated.【Result and conclusion】The ATCOR2 model was not suitable for building broadleaved forest LAI-VI regression model;in addition to the RVI,for FLAASH model and 6S model,LAI of broadleaved forest had a good correlation with EVI,MSAVI.Among them the power function model of LAI-MSAVI with FLAASH model yield the best goodness of fit.LAI estimation precision of FLAASH model was superior to the 6S model for broadleaved forest.With the aid of remote sensing technology to quantitatively extract vegetation physiological parameters,suitable atmospheric correction model should be selected prudently.
remote sensing;leaf area index;atmospheric correction
S718.5
A
1001-411X(2014)03-0100-05
2013-01-12 优先出版时间:2014-03-31
优先出版网址:http:∥www.cnki.net/kcms/doi/10.7671/j.issn.1001-411X.2014.03.018.html
顾哲衍(1990—),男,硕士研究生,E-mail:ah_gzy@163.com;通信作者:张金池(1965—),男,教授,博士,E-mail: nj_zjc@163.com
国家自然科学基金(31200534);长三角水源区面源污染林业生态修复技术研究(201104055-1);江苏省2009年度研究生科研创新计划项目;南京林业大学高学历人才基金项目;江苏省高等学校林学优势学科建设项目(164010641)
顾哲衍,张金池,林 杰,等.大气校正模型对阔叶林叶面积指数遥感估算的影响[J].华南农业大学学报,2014,35(3):100-104.
