钙碱性火成岩的角闪石全铝压力计——回顾、评价和应用实例

汪洋

中国地质大学(北京)地球科学与资源学院，北京，100083

内容提要: 定量地获得岩体结晶时的压力，对于探讨其剥蚀深度及了解造山带的构造热演化史等方面有重要意义。对于钙碱性侵入岩而言，可以应用角闪石全铝压力计对钙碱性火成岩结晶压力进行估计。对于不同角闪石压力计公式的选择，前提是满足它们各自的适用条件，否则所得结果没有意义。角闪石全铝压力计不能用于估算A型花岗岩的结晶压力，更不能用于计算变质岩的变质压力。对于结晶温度低于750℃的钙碱性中酸性岩体而言，Anderson和Smith(1995)的温度校正意义不大。Ridolfi等(2010)提出的指数关系角闪石压力计公式适用于钙碱性火山岩中角闪石斑晶的结晶压力估算。Uchida等(2007)的黑云母全铝压力计缺乏理论和实验基础，不建议使用。应用角闪石全铝压力计所得到薛家石梁—黑山寨复式岩体侵位深度的区域变化，指示了云蒙山变质核杂岩下盘的掀斜；低角度正断层(拆离断层)可以通过高角度正断层的掀斜旋转而形成。

如何定量地获得火成岩，尤其是侵入岩, 结晶时的压力，进而得到岩体的侵位深度或火山岩岩浆房的深度，对于探讨岩浆作用过程的物理机制，以及了解剥蚀深度、约束造山带的构造热演化史等方面有着重要意义(Anderson, 1996; Anderson et al., 2008)。令人遗憾的是，由于岩浆岩的主要造岩矿物在结晶过程中的相平衡反应的熵变化大而体积变化小，对压力并不敏感，所以适用于岩浆岩体系的地质压力计并不多(Philipotts and Ague, 2009)。对于常见的钙碱性岩浆岩，可以应用角闪石全铝压力计对结晶压力进行估计(Hammarstrom and Zen, 1986; Anderson et al., 2008)。然而，角闪石全铝压力计存在多种版本的回归公式，对使用者造成了困扰。还有一些研究者不顾及角闪石全铝压力计的适用条件，将其应用于A型花岗岩的结晶压力估计(张拴宏等, 2007)，甚至用于估计角闪岩相变质岩的变质压力(涂文传等, 2013)。因此，本文在系统回顾角闪石全铝压力计的基础上，对该压力计的适用条件、回归公式选择等方面进行了总结；同时列举了应用角闪石全铝压力计解释地质构造的若干实例。

Uchida等(2007)认为可以应用钙碱性长英质侵入岩中黑云母的全铝含量估算岩体的结晶压力。这种黑云母全铝压力计已在国内学者的研究中被多次应用(王建平等, 2009; 骆文娟等, 2010; 康志强等, 2010; 李晓伟等, 2011; 东前等, 2011; 刘学龙等, 2013)。但是，黑云母全铝压力计只是针对日本有限地区的数据进行经验标定得出的，其普遍适用性和真实性有待验证。所以，本文利用几个典型钙碱性岩体的矿物成分数据，对黑云母全铝压力计进行了检验，探讨其是否可靠。

1 适用于侵入岩的角闪石全铝压力计

1.1 线性关系角闪石全铝压力计

Hammarstrom和Zen(1986)通过接触变质矿物组合、冷却史、地层学重建等方法对科迪勒拉造山带的钙碱性侵入岩体进行了研究，指出钙碱性岩体在近固相线下的结晶压力与角闪石的全铝含量(Altot)的线性关系经验公式：

P=-0.392 + 0.503n(Altot)r2= 0.80

(1)

公式(1)中P的单位是GPa，n(Altot)为角闪石分子式中全部Al(即包括Ⅳ和Ⅵ次配位的Al)的摩尔分数。误差为±0.3GPa。

角闪石全铝压力计的基础是相律。在9相(角闪石+黑云母+斜长石+碱性长石+石英+ Fe—Ti氧化物+熔体+流体相)、10组分(SiO2—TiO2—Al2O3—Fe2O3—FeO—MgO—CaO—Na2O—K2O— H2O)体系中存在三个自由变量，即：氧逸度、温度和压力。当氧逸度由二价铁钛氧化物或绿帘石所缓冲，同时温度接近于等温固相线(存在花岗质流体)时，压力便为唯一的变量，此时压力是角闪石中全铝含量的唯一影响因素(Schmidt, 1992)。

Hollister等(1987)在Hammarstrom和Zen工作的基础上增加统计数据量，扩展了适用的压力范围，得到下列经验公式：

P=-0.476 + 0.564n(Altot)r2= 0.97

(2)

公式(2)中P的单位是GPa，n(Altot)为角闪石分子式中Al的摩尔分数，误差为 ±0.1GPa。Hollister等(1987)的理论分析表明：当结晶压力高于0.2 GPa时，含角闪石的钙碱性岩浆其固相线对压力不敏感，并且温度变化范围最多不超过100℃；而当结晶压力低于0.2 GPa时，固相线温度随压力降低显著升高，导致温度对角闪石中的全铝含量的影响更为显著；所以，角闪石的全铝含量与压力之间线性回归关系式只适用于结晶压力高于0.2 GPa的情况。

Johnson和Rutherford(1988, 1989)通过在H2O、CO2饱和，760℃，压力大于0.2 GPa条件下的实验，验证并标定了角闪石全铝含量与结晶压力的相关关系，得到线性回归公式：

P=-0.354 + 0.428n(Altot)

(3)

P=-0.346 + 0.423n(Altot)r2= 0.99

(4)

公式(3)和(4)中P的单位都是GPa，n(Altot)为角闪石分子式中Al的摩尔分数，公式(4)的误差为±0.05 GPa。

Schmidt(1992)通过在H2O饱和，675℃，压力大于0.2 GPa条件下的实验，标定角闪石全铝含量与结晶压力的相关关系为：

P=-0.301+0.476n(Altot)r2= 0.99

(5)

公式(5)中P的单位是GPa，n(Altot)为角闪石分子式中Al的摩尔分数，误差为±0.06 GPa。

因此，公式(1)和(2)属于经验公式，而公式(3)、(4)、(5)为实验标定的结果；后者具有更高的精度。由于公式(3)是Johnson和Rutherford(1988)发表在AGU会议摘要集中的结果，而公式(4)是他们发表在同行评议的学术刊物上的结果，所以后来的研究者在公式(3)、(4)之间多选用后者。

Anderson和Smith(1995)认为，应用角闪石全铝压力计时还应该考虑温度和氧逸度对角闪石阳离子占位的影响，适用于该压力计的角闪石n(Fetot)/[(n(Fetot)+n(Mg)]应当在0.40 ～ 0.65之间；明显超过此范围的角闪石成分数据不能用于估算压力。Anderson和Smith(1995)根据Johnson和Rutherford(1989)(高温)与Schmidt(1992)(低温)实验结果，应用内插法，得到含温度校正项的角闪石全铝压力计公式：

P=4.76n(Altot)-3.01-{[t-675]/85}×{0.530n(Altot)+0.005294[t-675]}

(6)

公式(6)中压力P的单位是108Pa(即kbar)，t为摄氏温度。Anderson和Smith推荐使用Blundy和 Holland(1990)、Holland和Blundy(1994)的角闪石—斜长石温度计估算岩浆的近固相线温度。

图1 角闪石全铝含量[n(Altot)]与近固相线温度(t)约束的结晶压力等值线图[据Anderson和Smith(1995)公式计算]Fig. 1 The contour map of the crystallization pressure calculated by the Al-in-hornblende [n(Altot)] and the near solidus temperature (t) [ according to the formula of Anderson and Smith (1995)]

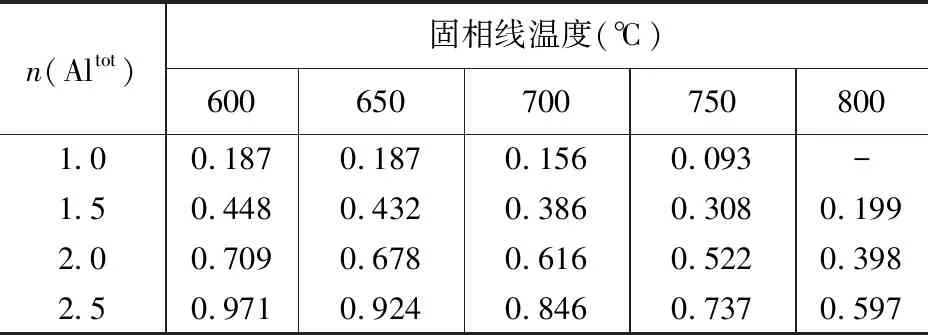
有证据显示，Anderson和Smith(1995)的温度校正没有太大的必要性。首先，当岩体的固相线温度低于750℃时，对应于 50℃的温度校正值，应用Anderson和Smith(1995)的全铝压力计公式计算得到的压力值与未经温度校正的压力值之间的偏差在 0.01 ～ 0.08 GPa之间(图1, 表1)，与其它角闪石全铝压力计线性公式的固有误差( 0.06 ～ 0.1 GPa)相当。对于钙碱性酸性(SiO2> 67%)岩体而言，当结晶压力在0.2 GPa以上时，其流体饱和的近固相线温度一般不大于750℃，多数在650 ～ 720℃之间(Wyllie,1971; Hollister et al., 1987; Anderson et al., 2008)。其次，斜长石—角闪石温度计估计的固相线温度很可能不准。这是因为侵入岩中的斜长石在固相线温度下常常与碱性长石发生再平衡反应，而角闪石也不一定是近固相线的结晶产物，导致斜长石—角闪石温度计估计的固相线温度不准确(Ague and Brandon, 1996; Blundy and Cashman, 2008)。因此，除非有明显证据表明岩体具有较高(≥ 750℃)的固相线温度，否则对于在流体饱和的近固相线条件下结晶的钙碱性中酸性岩体而言，Anderson和Smith(1995)的温度校正意义不大。相反，斜长石—角闪石温度计自身误差的传播会导致压力估算结果的误差增大。

表1 根据Anderson和Smith(1995)公式计算的不同固相线温度时角闪石全铝压力值

Table 1 The estimated pressures corresponding to the different solidus temperatures using the Al-in-hornblende barometer by Anderson and Smith (1995)

n(Altot)固相线温度(℃)6006507007508001.00.1870.1870.1560.093-1.50.4480.4320.3860.3080.1992.00.7090.6780.6160.5220.3982.50.9710.9240.8460.7370.597

注：压力单位是GPa。n(Altot)为角闪石分子式中Al的摩尔分数。- 代表计算值为负数，无实际意义。

综合上述，对于线性角闪石全铝压力计公式而言，其应用的前提条件是：

(1)由于标定实验的压力范围均在0.2 ～ 1.3 GPa(Johnson and Rutherford, 1989; Schmidt, 1992)，而且理论分析也表明经验公式(1)和(2)针对结晶压力应该高于0.2 GPa(Hollister et al., 1987)。同时，Uchida等(2007)应用闪锌矿压力计经验性地标定了日本5个岩浆热液矿床的成矿岩体的角闪石全铝压力计，其结果表明结晶压力小于0.2 GPa时，角闪石全铝含量与岩体结晶压力之间线性回归关系的斜率明显低于前述各线性关系式(参见第3节)。因此，上述各公式仅适用于结晶压力大于0.2 GPa的钙碱性侵入岩类的压力估算，而这一点常常被人们忽视。

(2)钙碱性岩石的矿物组合为角闪石+黑云母+斜长石+碱性长石+石英+Fe—Ti氧化物+榍石，当岩石矿物组合中缺少碱性长石和黑云母时则不适用。

(3)该压力计所要求的9相10组分体系平衡中，碱性长石只有在近固相线时才会稳定存在。因此，只有在近固相线温度条件结晶的角闪石，其全铝含量才能用于计算结晶压力。即：公式(3)、(4)的应用前提是岩体的固相线温度接近760℃，公式(5)的应用前提是岩体的固相线温度近似为675℃。对于钙碱性酸性(SiO2> 67%)岩体而言，当结晶压力在0.2 GPa以上时，其流体饱和的近固相线温度多数在620 ～ 700℃之间。所以，Schmidt(1992)的公式更适用于大多数钙碱性岩体的结晶压力估算。除非能比较准确地得到岩浆的固相线温度值，否则Anderson和Smith(1995)的温度校正公式意义有限。

(4)目前的角闪石全铝压力计适用于相对氧化条件下结晶的钙碱性侵入岩。A型花岗岩中的碱性角闪石在相对还原条件下结晶，不适用角闪石全铝压力计。

(5)角闪石全铝压力计不能用于估算变质岩的变质压力。近来，有的岩石学教科书(于炳松等, 2012)将角闪石全铝压力计作为适用于变质岩的压力计加以介绍，还有学者应用角闪石全铝压力计估算动力变质岩的成岩压力(涂文传等, 2013)。固态条件下的变质作用过程不满足角闪石全铝压力计成立的相平衡条件，这种做法是错误的。

1.2 幂函数关系角闪石全铝压力计

最近，汪洋(2013)根据根据Uchida等(2007)应用闪锌矿压力计标定的P< 0.2 GPa固结岩体的角闪石全铝含量，采用幂函数形式回归得到：

P=0.0823 [n(Altot)]2.401r2= 0.89

(7)

公式(7)中压力P的单位是GPa，n(Altot)为角闪石分子式中Al的摩尔分数，适用于结晶压力小于0.2 GPa的钙碱性侵入岩(图2)。

图2 线形与幂函数关系形式的侵入岩角闪石全铝压力计对比图Fig. 2 The comparison among the linear and the power function style Al-in-hornblende barometers 粗实线为汪洋(2013)适应于P < 0.2 GPa的压力计公式回归曲线；细实线为依据Schmidt(1992)实验数据得到的压力计公式回归公式，其中直线为Schmidt(1992)的结果，曲线为汪洋(2013)的幂函数回归曲线；断续线为依据Johnson和Rutherford(1989)实验数据得到的压力计公式回归公式，其中直线为Johnson和Rutherford(1989)的结果，曲线为汪洋(2013)的幂函数回归曲线。其中，实心圈代表来自Uchida等(2007)的数据，十字符号数据来自Schmidt(1992)的数据，空心圈代表来自Johnson和Rutherford(1989)的数据 The bold line is the regression curve suitable for P < 0.2 GPa (Wang, 2013). The thin line and curve represent the linear and power function regression for the Schmidt (1992) experimental data, respectively. The dashed line and curve represent the linear and power function regression for the Johnson and Rutherford (1989) experimental data, respectively. The solid circles are from Uchida et al. (2007), the crosses are from Schmidt (1992), and the open circles are from Johnson and Rutherford (1989)

基于Hollister等(1987)的理论研究，钙碱性侵入岩的角闪石全铝含量在小于0.2 GPa和大于0.2 GPa压力区间内对压力的敏感程度不同。因此，汪洋(2013)应用幂函数形式分别对Johnson和Rutherford(1989)与Schmidt(1992)的实验数据进行回归，得到如下全铝压力计公式：

P= 0.1307 [n(Altot)]1.842r2=0.98

(8)

P= 0.2154 [n(Altot)]1.524r2= 0.99

(9)

式中P的单位是GPa，n(Altot)为角闪石分子式中Al的摩尔分数。公式(8)适用于固相线温度高于700℃ 的情况(Johnson and Rutherford，1989)，公式(9)适用于固相线温度低于700℃的情况(Schmidt，1992)(图2)。从图2可以看出，在0.2 ～ 1.3 GPa压力范围内，幂函数与线性的压力计公式给出的结果非常接近。

如果可以较准确地估计固相线温度，可以采用内插法将公式(8)、(9)合并为：

P= 0.1307 (1+b) [n(Altot)]1.842 (1+a)

(10)

该公式中a=2.0298×10-3(760-t)，b=7.6178×10-3(760-t)，温度t的单位是℃。上述(8)、(9)、(10)公式适用压力范围不超出实验数据0.2 ～ 1.3 GPa的压力标定范围；其他条件与公式(1)～(6)相同。

采用幂函数形式的优点是：在小于0.2 GPa的区间内角闪石全铝含量随压力变化而变化的斜率较小，而在大于0.2 GPa压力区间内角闪石全铝含量随压力变化而变化的斜率较大(与已有实验标定数据一致)(图2)。所以，一旦有小于0.2 GPa压力区间的角闪石全铝含量随压力改变的实验岩石学数据，就可以将小于0.2 GPa和大于0.2 GPa压力区间内角闪石全铝含量的变化函数统一起来，归纳出适用于0 ～ 1.3 GPa的角闪石全铝压力计公式。

2 适用于火山岩的指数关系角闪石全铝压力计

Ridolfi等(2010)根据前人实验结果，对Johnson和Rutherford(1989)、Schmidt(1992)及Anderson和Smith(1995)压力计进行标定，发现其应用于中酸性火山岩时，计算的喷发前压力值与地质、地球物理资料估计的结果之间往往存在很大偏差。他们在系统搜集大量实验数据对角闪石全铝压力计重新进行检验的基础上，发现并不是所有的实验数据都适用于标定压力计公式；经过对实验数据和矿物成分数据的重新筛选，在满足相平衡的前提下提出了新的角闪石全铝压力计公式：

P=19.209 exp[1.438n(Altot)]r2=0.99

(11)

公式(11)中压力P的单位是MPa，n(Altot)为角闪石分子式中Al的摩尔分数，适用于钙碱性火山岩中产出的钙质角闪石，要求其成分满足：Al#≤ 0.21且n(Mg)/[n(Mg)+n(Fe2+)] > 0.5。

这个指数关系全铝压力计公式应用Ridolfi等(2010)文中所附软件可直接判别钙碱性岩类的角闪石成分数据是否适用于计算结晶压力，若适合则可得到压力估计值及其误差。需要注意的是，公式(11)不适用于地幔来源的角闪石的压力估计。

Ridolfi等(2010)应用公式(11)对全球20余座活火山喷发的钙碱性火山岩的角闪石斑晶成分进行了压力估算，得到的角闪石结晶压力所对应的岩浆房深度与地球物理证据吻合度很高。

Ridolfi等的指数形式角闪石全铝压力计公式与传统的线性角闪石全铝压力计公式相比，在全铝含量[n(Altot)]1.1 ～ 2.7范围内估算出的压力值偏低(图3)。其原因是：指数形式角闪石全铝压力计估算的是角闪石在熔体中结晶时的压力值，即角闪石的结晶温度可能显著高于熔体的固相线温度；相反，只有在近固相线温度下结晶的角闪石成分才能应用传统的线性角闪石全铝压力计公式估算其结晶压力。也就是说，指数形式角闪石全铝压力计适用于估算火山岩斑晶结晶时的压力，而不适用于计算侵入体的结晶压力。

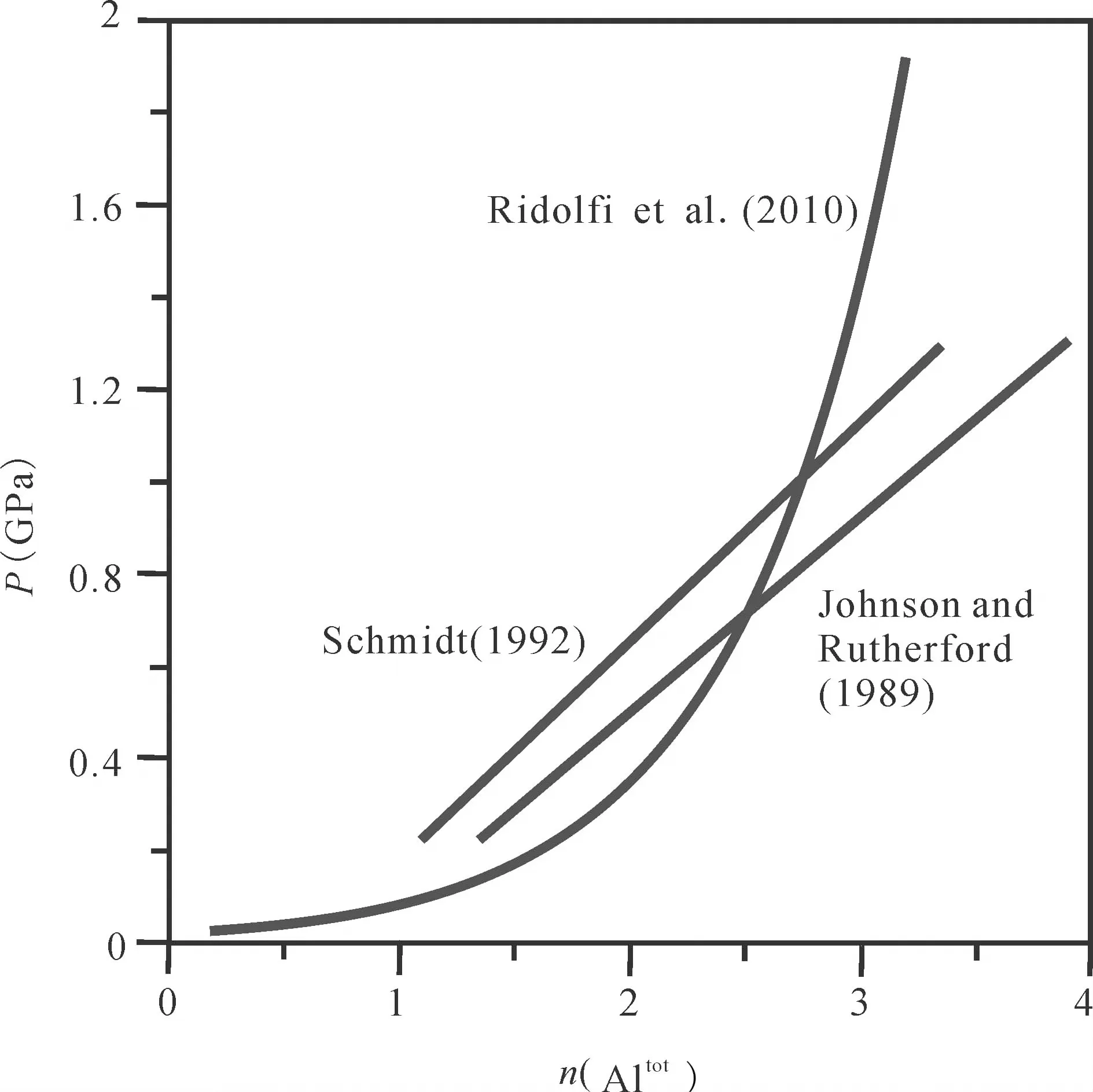
图3 指数关系与线性关系角闪石全铝压力计比较图解Fig. 3 The comparison between exponential and linear Al-in-hornblende barometers

3 黑云母全铝压力计

P=0.303×n(Altot)-0.65

(12)

公式(12)中压力P的单位是GPa，n(Altot)为黑云母分子式(基于O = 22)中Al的摩尔分数，误差为±0.033 GPa。一部分国内学者已开始使用该公式估算岩体的成岩深度(王建平等, 2009; 骆文娟等, 2010; 康志强等, 2010; 李晓伟等, 2011; 东前等, 2011; 刘学龙等, 2013)。

然而，Uchida等给出的黑云母全铝含量与同岩体的角闪石全铝含量之间的线性相关性并不显著，公式(12)的相关系数r2仅为0.36(参见Uchida et al., 2007的图5)，而且黑云母全铝压力计的建立缺乏相平衡理论依据和实验标定；因此Uchida等(2007)的黑云母全铝压力计不一定适用于估算钙碱性侵入岩的结晶压力。

根据美国西部Tuolumne岩基(Gray et al., 2008)、八达岭岩基(白志民等, 1991)和胶东地区钙碱性侵入岩(林景仟等, 1992)的矿物成分数据，作者对黑云母全铝压力计的可靠性进行了检验。由于黑云母全铝压力计被认为仅适用于压力小于0.2 GPa的侵入岩，所以应用汪洋(2013)提出的公式(7), 适用于低压(P< 0.2 GPa)的角闪石全铝压力计公式, 对黑云母全铝压力计进行验证。由于Ridolfi等的角闪石全铝压力计可以适用于低压范围，所以同时采用Ridolfi等(2010)的指数关系角闪石全铝压力计公式(11)与黑云母全铝压力计的估算结果进行比对。

结果发现，黑云母全铝压力计估算的压力值与两类角闪石压力计公式所估算的压力值之间的偏差均十分显著，线性相关性很差(图4)。这表明钙碱性侵入岩中黑云母的全铝含量与角闪石的结晶压力之间不存在明显的相关性。因此，Uchida等(2007)的黑云母全铝压力计不能用来估计岩浆岩的结晶压力，冒然使用该公式会导致错误的结论。

图4 利用两种角闪石全铝压力计对黑云母全铝压力计的标定图解Fig. 4 The calibration of the Al-in-biotite barometer by two kinds of Al-in-hornblende barometers PW为公式(7)计算所得压力(汪洋, 2013)；PR为公式(11)计算所得压力(Ridolfi et al., 2010)；PBi为黑云母全铝压力计，公式(12)计算所得压力(Uchida et al., 2007)。图中实线代表两种压力计公式相关系数等于1的理想状况，断续线是根据实际数据拟合的两种压力计公式所得结果的相关关系直线。方块为美国西部Tuolumne岩体数据(Gray et al., 2008)；菱形为八达岭岩基数据(白志民等, 1991)；圆圈为胶东地区钙碱性侵入岩数据(林景仟等, 1992)。 PW : according to the formula (7) (Wang Yang, 2013); PR: according to the formula (11) (Ridolfi et al., 2010); PBi: according to the formula (12), i.e., the Al-in-biotite barometer (Uchida et al., 2007). The solid line represents the ideal situation in which the regression coefficient equals 1 between the data obtained by two barometers, but the dashed line is the actual regression. The squares represent the data from the Tuolumne batholith of western USA (Gray et al., 2008), the diamonds are the data from the Badaling batholith of Beijing (Bai Zhimin et al., 1991), and the circles are the data from the calc-alkaline plutons of eastern Shandong area (Lin Jingqian et al., 1992)

4 应用实例

角闪石全铝压力计已被广泛用于估算钙碱性侵入岩的侵位深度(例如：Ague and Brandon, 1996; Stein and Dietl, 2001; 张拴宏等, 2007; 雷敏等, 2010; 刘春花等, 2013)，合理运用角闪石全铝压力计可以为深入了解研究区的地质构造演化提供重要信息(Anderson et al., 2008)。

4.1 云蒙山变质核杂岩下盘掀斜的岩体侵位深度证据

薛家石梁—黑山寨复式岩体出露于云蒙山变质核杂岩河防口拆离断层的下盘(西北侧)，由上庄辉石岩—辉长岩、薛家石梁闪长岩、黑山寨石英二长岩和湖门二长岩组成；在平面上呈长轴北西—南东向展布的似椭圆状，基性岩出露于东南端，而偏酸性端元出露在西北部；复式岩体中的闪长岩、石英二长岩与二长岩之间为过渡接触关系，属于典型的钙碱性岩石(图5)。黑熊山花岗岩是后期侵入的另一个岩体，而非薛家石梁原始岩浆的直接分异产物(汪洋, 2007)。

薛家石梁—黑山寨复式岩体的闪长岩、石英二长岩、二长岩满足9组分10相的要求，同时其角闪石n(Fetot)/[n(Fetot)+n(Mg)]比值在0.35 ～ 0.65之间。薛家石梁—黑山寨复式岩体岩石为中—粗粒结构，反映其结晶深度较大，其锆饱和温度(高于岩浆的固相线温度)在650 ～ 760℃之间，因此岩浆的固相线温度一定在700℃以下；所以采用Schmidt(1992)公式估算该岩体的结晶压力。估算结果表明：薛家石梁—黑山寨复式岩体东南部上庄村北东出露的闪长岩结晶压力约0.6 GPa、侵位深度约22 km(地壳密度取2.8×103kg/m3，下同)，位于复式岩体中段南侧西湖村出露的湖门二长岩结晶压力约0.36 GPa、侵位深度约15 km，复式岩体中部花果山村以北出露的石英二长岩结晶压力0.21 GPa、侵位深度约8 km(表2)。据此可以推断出薛家石梁—黑山寨复式岩体经历了南东—北西向掀斜作用，导致其原始的底部出露于东南部，而顶部出露于西北部。美国西北部华盛顿州Baja British Columbia地区的Mount Stuart岩基也有类似情况(Ague and Brandon, 1996)。

角闪石压力计的估算结果同时显示：薛家石梁—黑山寨复式岩体东侧出露的长园闪长岩的结晶压力是0.65 GPa、侵位深度约24 km。野外观察表明，长园闪长岩发育同构造片麻理，其侵位深度应当在脆性变形域之下(姬广义等, 2004)，这与角闪石全铝压力计推断的24 km侵位深度之间有很好的对应性。位于薛家石梁—黑山寨复式岩体和长园闪长岩的西北侧的磨石口二长闪长岩、水泉沟二长闪长岩和铁炉子二长闪长岩的结晶压力分别为0.46 GPa、0.27 GPa和0.34 GPa，对应的侵位深度分别为约17 km、10 km和12 km(表2)。

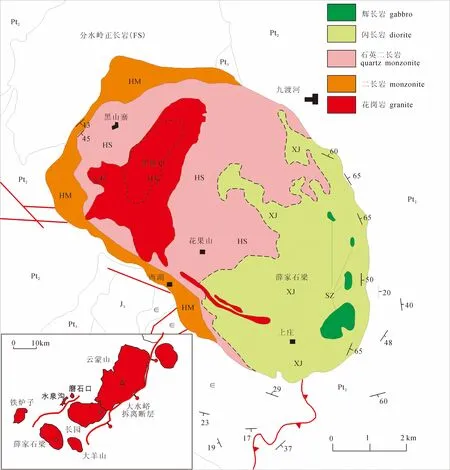
图5 云蒙山薛家石梁—黑山寨复式岩体地质简图(据Wang and Yao, 2013修改)Fig. 5 The simplified geological map of Xuejiashiliang—Heishanzhai composite pluton in Yunmeng Mountain area (modified after Wang and Yao, 2013) J3—上侏罗统髫髻山组；∈—寒武系；Pt3—新元古界下马岭组—景儿峪组；Pt2—中元古界蓟县系。 FS—分水岭正长岩； HM—湖门二长岩；HS—黑山寨石英二长岩；HX—黑熊山花岗岩；SZ—上庄辉长岩；XJ—薛家石梁闪长岩 J3—Upper Jurassic Tiaojishan Formation； ∈—Cambrian； Pt3—Neoproterozoic Xiamaling Formation — Jing’eryu Formation； Pt2—Mesoproterozoic Jixian Series. FS—Fenshuiling syenite； HM—Humen monzonite； HS—Heishanzhai quartz monzonite； HX—Heixiongshan granite； SZ—Shangzhuang gabbro； XJ—Xuejiashiliang diorite.

在平面位置上，薛家石梁—黑山寨复式岩体东南端、长园闪长岩较磨石口、水泉沟和铁炉子二长闪长岩更靠近NNE—SSW走向的云蒙山变质核杂岩河防口拆离断层，结合这些岩体的侵位深度估算结果，作者推断河防口拆离断层下盘已发生掀斜，即靠近河防口拆离断层的南东侧地区构造层次较深，而远离河防口拆离断层的北西侧地区构造层次较浅。薛家石梁—黑山寨复式岩体的掀斜是河防口拆离断层下盘(即云蒙山变质核杂岩下盘)运动的结果，即：变质核杂岩下盘在剥露过程中的背形穹弯作用导致侵入其中的薛家石梁—黑山寨复式岩体发生大角度掀斜。长园闪长岩的侵位年代为151 Ma，磨石口、水泉沟和铁炉子二长闪长岩均为早白垩世早期侵位(133 ～ 137 Ma)(郁建华等, 1994; 鲍亦刚等, 2001; 孙志明等, 2007; 焦守涛等, 2013)，薛家石梁—黑山寨复式岩体的侵位年代为125 Ma，云蒙山变质核杂岩发育于125 Ma(Davis et al., 2001)，因此河防口拆离断层下盘的掀斜作用发生在125 Ma之后。云蒙山变质核杂岩下盘的掀斜指示，低角度正断层(拆离断层)很可能是高角度正断层在运动过程中随下盘旋转掀斜而导致断层面倾角变缓的结果(Wernicke and Axen, 1988; Buck, 1993; Lavier et al., 1999; Wang and Yao, 2013)。

4.2 北京西山早白垩世岩浆房、岩体侵位深度及其地质意义

北京西山地区出露的髫髻山组安粗岩属于典型的高钾钙碱性火山岩(汪洋等, 2001)，其顶部火山岩层的锆石U-Pb年龄为137 Ma(袁洪林等, 2005)，下伏地层的沉积年龄介于147 ～ 144 Ma之间(Yang et al., 2006)(图6)。

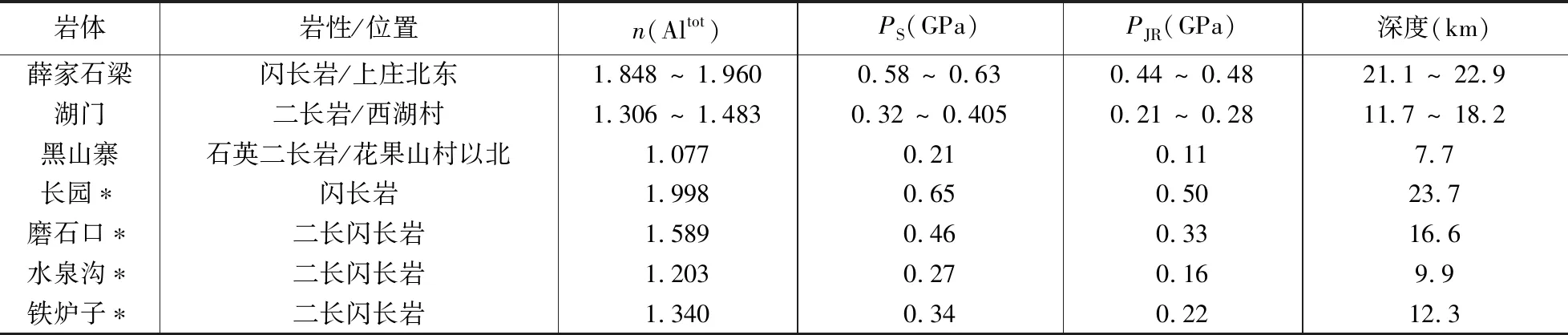
表2 云蒙山薛家石梁—黑山寨复式岩体及相邻岩体侵位深度估算结果Table 2 The estimated emplacement depth for the Xuejiashiliang—Heishanzhai composite pluton and its neighboring plutons in Yunmeng Mountain area

注：PS为Schmidt(1992)公式计算所得压力；PJR为Johnson和Rutherford(1989)公式计算所得压力，与Schmidt(1992)公式计算值相对比。深度按Schmidt(1992)公式求得的压力计算。带*者角闪石原始成分据白志民等(1991)，其余为作者未发表数据。角闪石分子式按O=23计算。

对7个熔岩样品的角闪石斑晶电子探针分析表明：西山地区出露的髫髻山组火山岩中角闪石斑晶均属于镁绿钙闪石，而其全铝含量从1.8变化到2.36。应用Ridolfi等(2010)的角闪石全铝压力计公式及其配套的Excel表格，估算出角闪石斑晶的结晶压力变化范围0.26 ～ 0.57 GPa(表3)。有必要指出，Johnson和Rutherford(1989)压力计公式(即：公式4)所估算的压力值比Ridolfi等(2010)公式的结果高出0.08 ～ 0.16 GPa(表3)；而Anderson和Smith(1995)压力计(即：公式6)给出的是负数值，没有实际意义。这些角闪石斑晶的结晶温度很高(≥ 900℃，表3)，已经远远超出岩浆的固相线温度，所以前述公式(1)～(10)均不适用。

对意大利南部斯通博利火山喷出的钾玄岩、玄武粗安岩的研究显示，这些岩浆中斑晶的结晶压力为0.15 ～ 0.30 GPa(Cigolini et al., 2008)。结合地球物理证据，前人推断斯通博利火山地表下6 ～ 12 km深度存在长轴直立的瓶状(bottle-like)岩浆房，其垂向高度约6 km(Cigolini et al., 2008; Zellmer and Annen, 2008)。对北京西山地区髫髻山组火山岩中角闪石斑晶的压力估算结果显示其结晶的P—T条件不同，其所记录的压力条件变化于0.26 ～ 0.57 GPa之间(表3)。据此推断，在髫髻山组火山岩喷发时期，古地表之下9 ～ 21 km的深度存在高位岩浆房。由于长轴呈水平方向展布的岩浆房(岩体)其垂向厚度很难超过7 km，多在3 km以内(Cruden, 1998; Zellmer and Annen, 2008)，故而笔者推断西山地区髫髻山组火山岩的岩浆房形态很可能也是长轴直立的瓶状，其垂向高度约12 km。

当前对岩浆上侵的物理机制的研究表明：岩浆从源区分离运移过程中，决定其在地壳就位的最主要因素并非浮力，而是地壳中的流变学界面，其中脆—韧性转换带是决定上侵岩浆就位形成侵入体或岩浆房的重要物理界面(Vigneresse and Clemens, 2000)。这意味着早白垩世早期北京西山地区上部地壳的脆—韧性转换带大致位于10 ～ 20 km深度。

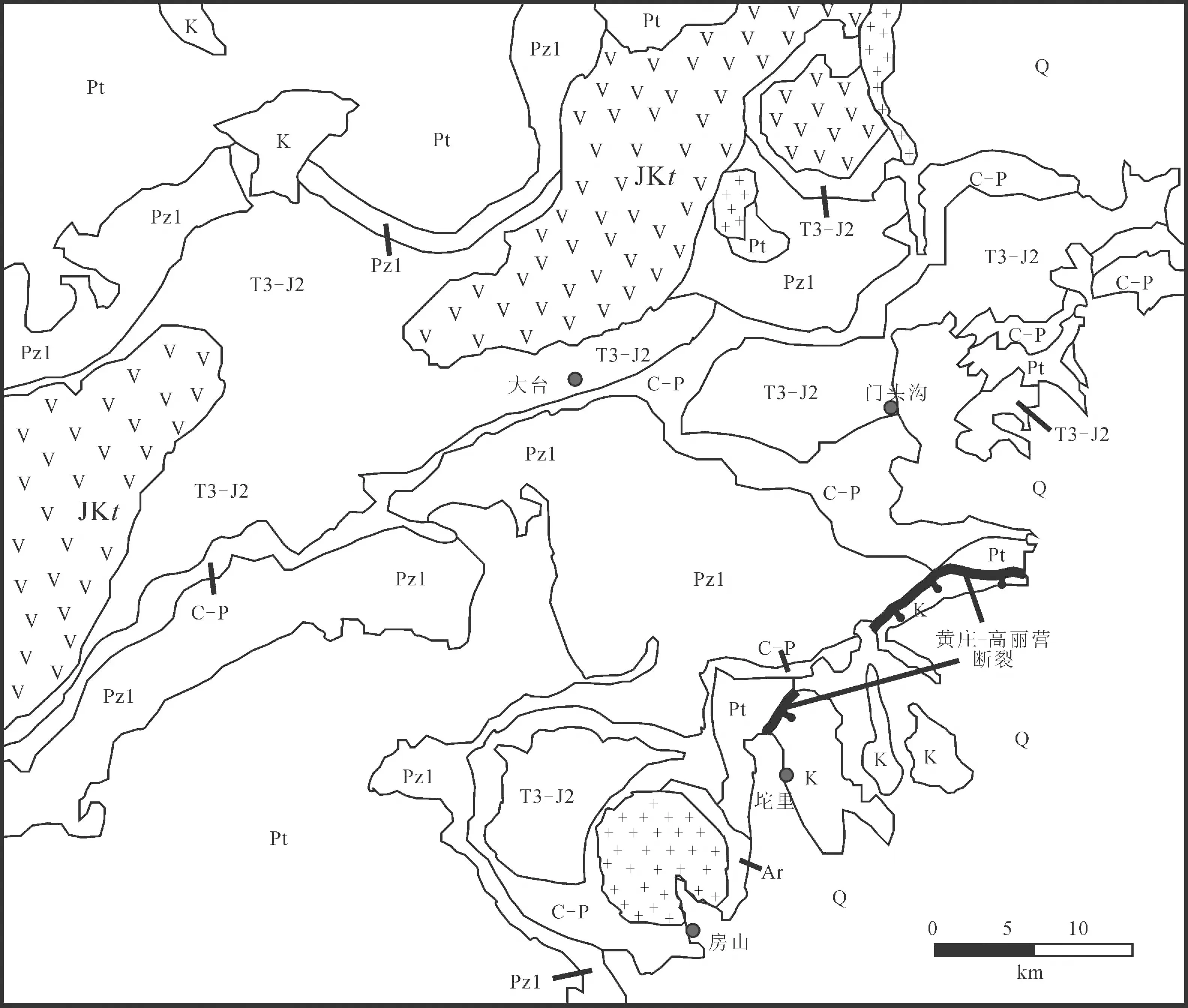
图6 北京西山地区东部地质简图(据鲍亦刚等, 2001简化)Fig. 6 The sketch geological map of the eastern part of Western Hills of Beijing (simplified after Bao Yigang et al., 2001) Q—第四系；K—白垩系；JKt—髫髻山组；T3—J2—上三叠统—中侏罗统；C—P—石炭系—二叠系； Pz1—下古生界；Pt—元古宇；Ar—太古宇 Q—Quaternary；K—Cretaceous strata； JKt—Tiaojishan Formation； T3—J2—Upper Triassic—Middle Jurassic; C—P—Carboniferous—Permian； Pz1—Lower Paleozoic； Pt—Proterozoic； Ar—Archean

房山岩体是北京西山地区出露的典型深成岩体(图6)，主要由外环的石英闪长岩和主体花岗闪长岩组成，含有大量的镁铁质微粒包体(MME)，其锆石U-Pb年龄为131 ～ 132 Ma(蔡剑辉等, 2005; 张金阳等, 2013)。岩相学观察表明，房山岩体及其所含镁铁质微粒包体的矿物组合满足9组分10相的要求，同时其角闪石n(Fetot)/[n(Fetot) +n(Mg)]比值在0.41 ～ 0.49之间。房山岩体为中—粗粒结构，反映其结晶深度较大，其锆饱和温度(高于岩浆的固相线温度)在650 ～ 760℃之间，因此岩浆的固相线温度一定在700℃以下；所以采用Schmidt(1992)公式估算该岩体的结晶压力。对于其中的镁铁质微粒包体，由于其固相线温度高于寄主岩浆，采用Johnson和Rutherford(1989)公式估算其中的角闪石结晶压力。在压力估算过程中，选取环带状角闪石颗粒外环的成分数据，此处最接近于近固相线条件下的平衡组分。计算结果见表4。

从表3可以看出，房山岩体的结晶压力为0.23 ～ 0.34 GPa，对应的深度在8.4 ～ 12.3 km之间。由于角闪石全铝压力计的误差为0.05 ～ 0.06 GPa，对应于1.8 ～ 2.2 km深度，可以取平均值10 km代表房山岩体的侵位深度。这意味着早白垩世早期北京西山东南部房山一带上部地壳的脆—韧性转换带大致位于10 km深度。

中、低地温梯度地区的上部地壳的脆—韧性转换带深度一般在15 km以上(Wang, 2001; Afonso and Ranalli, 2004; 汪洋, 2006)，上部地壳脆—韧性转换带深度约10 km表明北京西山地区在早白垩世早期(145 ～ 131 Ma)处于高地温梯度状态。结合该时期内北京西山强烈岩浆活动所反映的地壳下部的部分熔融状态，可以合理推断当时地壳的整体流变学强度低，这是早白世垩时期北京西山地区发生强烈构造变形的必要条件。

房山岩体10 km的侵位深度表明，其固结后经历了至少10 km的剥蚀。西山地区髫髻山组火山岩出露区位于房山岩体北西方向约20 km处(鲍亦刚等, 2001)。可以推算出北京西山地区在131 Ma之后发生过南东—北西方向约25°的掀斜。北东走向的黄庄—高丽营断裂出露于房山岩体北东侧，向南则隐伏于岩体以东的第四系之下(鲍亦刚等, 2001)；该断层的正断运动导致位于其下盘的北京西山地区发生掀斜。

表3 北京西山地区髫髻山组火山岩岩浆房深度估算结果Table 3 The estimated chamber depth for the Tiaojishan volcanic rocks in the Western Hills of Beijing

注：T、PR分别为Ridolfi等(2010)中的公式计算所得角闪石结晶温度与压力(用该文所附Excel表格直接得到)；PJR为Johnson和Rutherford(1989)公式计算所得压力，与Ridolfi等(2010)公式计算值相对比。深度按Ridolfi等(2010)公式求得的压力计算。角闪石原始成分来自笔者未发表数据。角闪石分子式按O=23计算。

表4 房山岩体及镁铁质微粒包体(MME)侵位深度估算结果Table 4 The estimated emplacement depth for the Fangshan pluton and its mafic micro-enclaves (MME)

注：MME的角闪石结晶压力按Johnson和Rutherford(1989)公式计算，其余按Schmidt(1992)公式计算。角闪石原始成分来自作者未发表数据。角闪石分子式按O=23计算。

5 结论

角闪石全铝压力计是目前针对钙碱性长英质岩浆岩结晶压力估计的可靠矿物学方法。自然条件下结晶过程很复杂，所得压力值难免存在一定的误差，但仍可以利用角闪石全铝压力计估算钙碱性侵入岩的结晶压力或火山岩中角闪石斑晶的结晶压力。笔者认为：

(1)应用角闪石全铝压力计公式的前提是满足其适用条件，否则所得结果没有意义。目前提出的大多数角闪石全铝压力计公式不适用于估计结晶压力低于0.2 GPa的情况。特别注意的是，A型花岗岩(铁质花岗岩)中角闪石富铁、形成于低氧逸度条件，不能够满足角闪石全铝压力计对氧逸度的要求；因此角闪石全铝压力计不能用于估算A型花岗岩(铁质花岗岩)的结晶压力。

(2)对于在流体饱和的近固相线条件下结晶的钙碱性中酸性岩体而言，Anderson和Smith(1995)的温度校正意义不大，相反会增大误差。

(3)Ridolfi等(2010)提出的指数关系角闪石压力计公式适用于钙碱性火山岩中角闪石斑晶的结晶压力估算，可以定量约束火山系统深部岩浆房的深度。

(4)Uchida等(2007)提出的黑云母全铝压力计缺乏理论基础和实验标定；其估算的压力值明显偏离角闪石全铝压力计所获结果，而且两者之间线性相关性很弱；不建议使用。

(5)应用角闪石全铝压力计对北京几个早白垩世钙碱性火成岩结晶压力的估算结果显示：云蒙山变质核杂岩下盘在低角度拆离断层活动过程中发生了明显的掀斜；高角度正断层在运动过程中下盘旋转掀斜导致断层面倾角变缓，可以导致低角度正断层(拆离断层)的形成。位于黄庄—高丽营正断层下盘的北京西山地区，在正断层活动过程中也发生了明显的掀斜。

致谢：吴春明教授和章雨旭研究员提出了宝贵的修改建议，姚瑶、吴小林帮助清绘图件，在此并致谢忱。