基于支持向量机的裂解炉燃料气热值软测量
2014-09-10郭强刘伟平
郭强,刘伟平
(辽宁石油化工大学 a. 信息与控制工程学院;b. 石油天然气工程学院,辽宁 抚顺 113000)
在乙烯装置中,最核心的设备是裂解炉,其中炉管出口温度是需要被首先考虑的被控对象之一,其控制结果的好坏将直接影响裂解深度和乙烯收率。裂解炉炉管的出口温度主要受裂解烃进料流量、稀释蒸汽流量、原料烃组成和燃料气热值的影响,通常在裂解烃进料流量、稀释蒸汽流量、原料烃组成等变量变化不大的情况下,燃料气热值的变化是影响炉管出口温度波动的主要变量。因此,若要保证炉管出口温度的相对稳定,可以采取实时测量燃料气热值,并通过前馈控制器前馈调节侧壁和底部烧嘴的燃气量的控制策略[1-2]。
目前炼化厂主要采用在线热值仪表测量燃料气热值,但在线热值仪表价格昂贵,难于维护。并且存在明显的测量滞后,一般为5~6 min[2],如果直接采用热值仪表分析值,由于存在测量滞后,当燃料气组分发生波动导致热值变化时,不能在热值变化实际影响出口温度之前,采取有效的控制策略提前消除热值干扰,将会影响到出口温度的稳定。为解决该问题,建立燃料气热值软测量模型就是一种有效的方法。
由于燃料气系统的化学反应机理复杂,传统的机理建模方法难以实现,因而一种基于人工智能的工业过程软测量技术越来越受到重视,如神经网络、遗传算法等。刘漫丹等[3]研究开发了基于模糊逻辑系统的小脑模型关节控制器神经网络算法。仿真研究表明,该算法提高了传统小脑模型关节控制器的平滑能力和泛化能力,将该算法用于热值软测量系统中,经过长期的现场应用实践,证实了该热值软测量系统具有较高的热值预测准确性。杨思远等[2]提出了一种基于小波神经网络的软测量结构,由于小波神经网络同时具有降噪变换和非线性映射的能力,用这种方法来“测量”裂解炉燃料气热值,可以通过提高现场数据的信噪比来保证该软测量系统的高精度和泛化能力。张照娟[4]在普通模糊神经网络的基础上引入了具有递归环节的动态模糊神经网络,并运用改进的粒子群算法优化模糊神经网络的模型参数,最后将此动态模糊神经网络应用于乙烯裂解炉燃料气热值的软测量建模中,取得了比较好的预测效果。
但是上述建模方法的推广能力很难得到保证,缘于其建模理论基于传统统计学。传统统计学运用经验风险最小化原则ERM(Empirical Risk Minimization)评价建模的效果,由于该原则只强调模型训练误差的极小而忽略对模型推广能力的要求,因而常常会导致过学习状态的发生,为此笔者提出一种基于支持向量回归机的软测量模型。
1 支持向量机
支持向量机SVM(Support Vector Machine)是20世纪90年代中期提出的一种机器学习算法,它的主要思想是建立一个分类超平面做为分划平面,使得正负两类点的“间隔”最大化。在支持向量机中可以使得经验风险为零,并使第二项最小化,因而从理论上保证了模型的最大泛化能力[5]。
1.1 支持向量机回归建模
xi∈Rn,yi∈R是从现场采集的输入输出样本,构成训练集合T={(xi,yi),i=1,…,l}。假设在训练集合T上模型输入输出间的非线性关系为f(x)。对于线性回归问题,支持向量机算法的目标是在训练集合T上寻找满足如下最优化问题的回归函数f(x):
(1)

(2)
((ωi·xi)+b)-yi≤ε+ξi
(i=1, 2, …,l)
(3)

式(1)~式(3)的对偶问题表示如下,这是求解该问题的常用方法:
(4)
(5)
(6)
现将式(4)~式(6)进行推广,使其可以处理非线性回归问题。这里的关键是引入核函数K(x,x′),通过核函数K(x,x′)的非线性变换能力,将输入空间转化到高维空间,并在高维空间中求解最优超平面,使低维线性不可分问题转化为高维线性可分问题。同时该种变换并不会增加计算复杂度,最优超平面仅仅涉及训练样本之间的内积运算x·x′。该种内积运算通过输入空间的函数就可以实现。基于该思想便产生如下的ε-支持向量回归机算法:
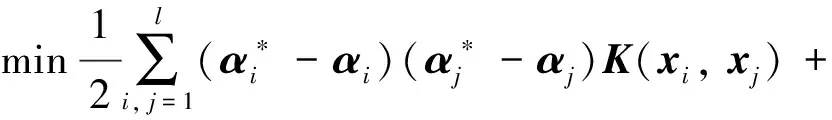
(7)
(8)
(9)
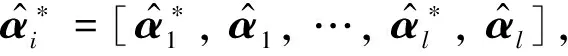
(10)
(11)
或
(12)
最后构造出回归函数:
(13)
SVM的体系结构如图1所示,SVM形式上类似于一个神经网络,模型的输出是中间节点的线性组合,每个中间节点对应一个支持向量[6]。
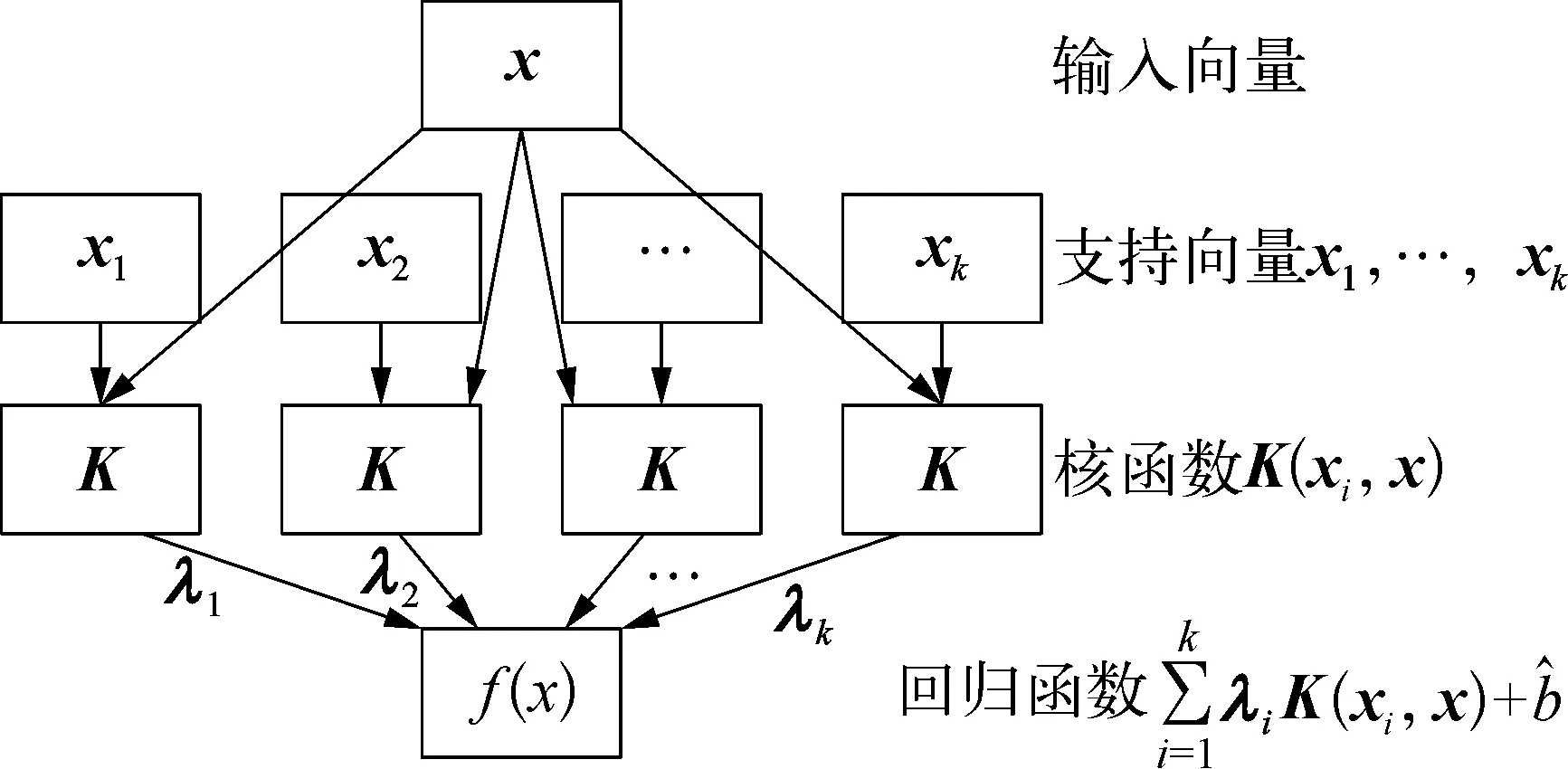
图1 SVM体系结构示意
2 热值软测量建模
在石油化工行业中,由于装置的化学反应机理复杂,外在干扰因素多,传统的机理建模方法往往难以实现,而软测量建模方法经过多年来的飞速发展,其理论体系已日趋完善,并且在石化行业中已有很多成功的应用实例。如裂解炉出口乙烯和丙烯收率的软测量、催化裂化分馏塔粗汽油干点软测量等[7]。文中运用上文论述的SVM原理,建立了燃料气热值的软测量模型。
2.1 工艺分析
某厂燃料气系统工艺流程如图2所示。

图2 燃料气系统工艺流程示意
正常情况下,乙烯装置自产甲烷气(伴有少量氢气和C2气体)并入燃料气储罐F1作为裂解炉燃料;动态工况下,乙烯装置自产甲烷气减少,燃料气储罐F1的压力发生波动,为了保持燃料气储罐压力的稳定,液化石油气(LPG)燃料并入燃料气储罐补足。因此,燃料气热值主要受燃料气的组分流量和压力波动的影响,可以选择燃料气流量(FIC-101-14)、燃料气压力(PIC-701)和LPG压力(PIC-702)作为软测量模型的输入变量,燃料气热值(AI-118)作为输出变量。软测量模型表示为y=f(x1,x2,x3),建模方法采用前述的支持向量回归机技术。
2.2 模型建立
模型建立的算法流程如图3所示。

图3 模型建立流程示意
1) 选定训练集和测试集。将从工业现场采集的260组数据分成2组,选择前130组作为训练集,后130组作为测试集。
2) 数据预处理。在进行正式的仿真训练前,由于各个变量的量纲不同,首先需要对样本数据进行归一化处理,归一化处理的方式有很多,这里采用[-1, 1]的归一化方式。
3) 训练和预测。数据经过预处理后,用训练集对SVM进行训练。在训练的过程中,可以选择出惩罚因子c和核函数参数g,通常这些参数的选取都是采用经验试凑的方法预先选取的,选出来的参数预测效果很差,经常会导致过学习或欠学习问题的发生。
3 软测量模型仿真结果
根据某厂裂解炉燃料气系统现场采集的数据,运用前述的支持向量回归机建模算法进行建模预测。首先对模型进行训练,在训练的过程中运用交叉验证法选出最优模型参数,如图4和图5所示。从图4~图5中上可以看出,模型的均方误差随模型参数c,g的变化趋势,并且当c=0.062 5,g=0.5时,模型取得最小均方误差0.043。
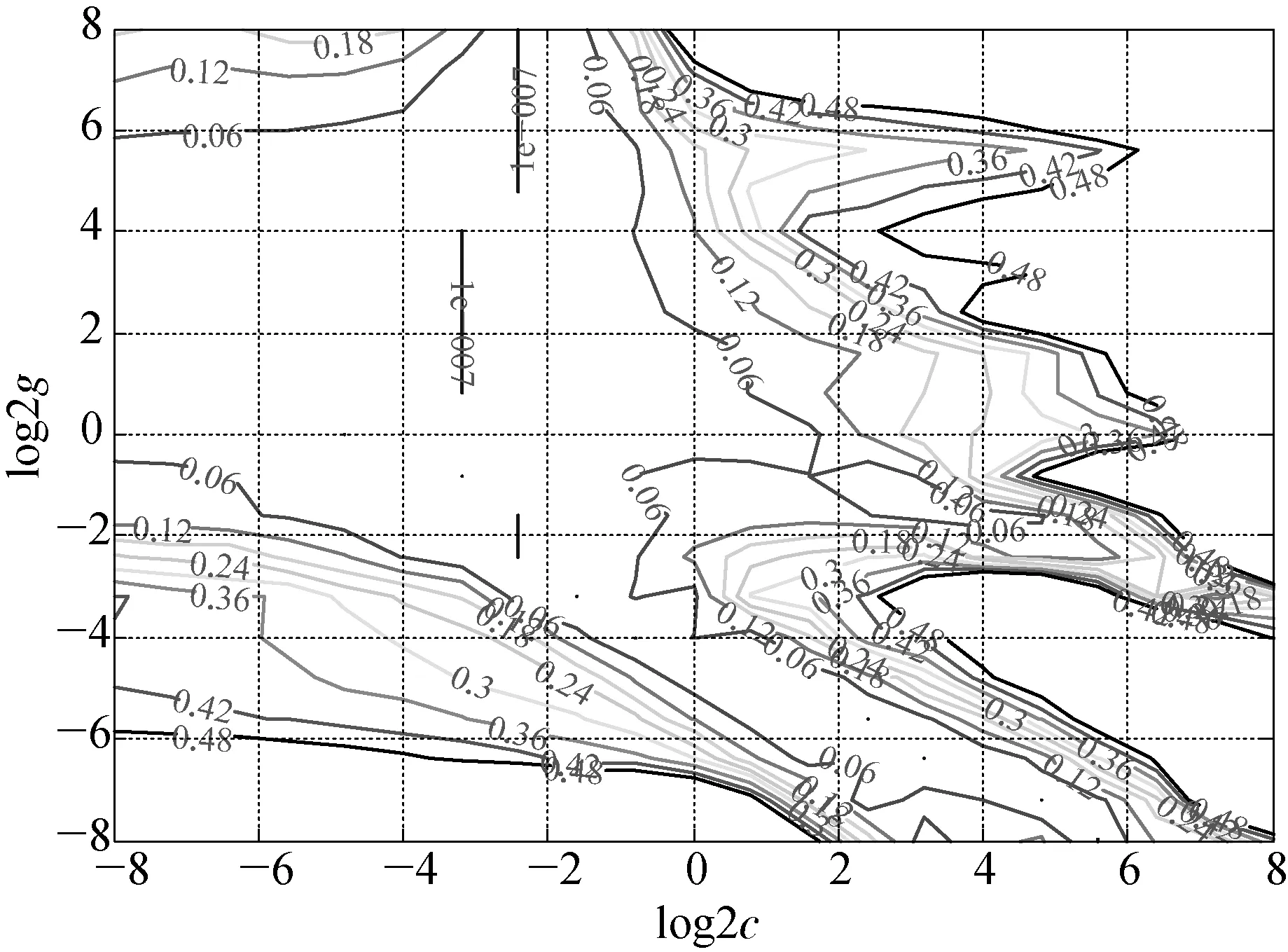
图4 SVM参数粗选择结果等高线示意
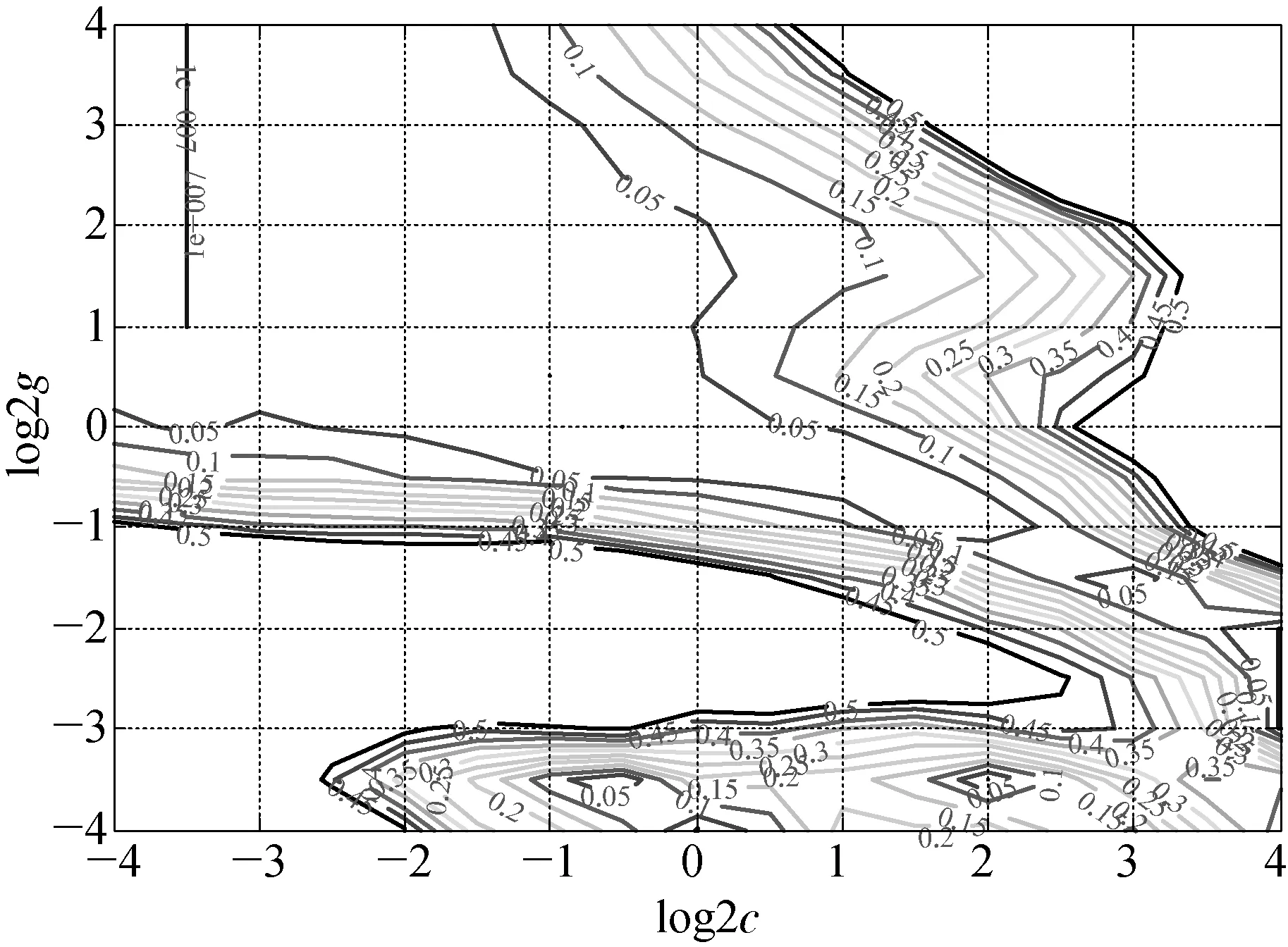
图5 SVM参数细选择结果等高线示意
图6和图7分别为测试数据和软测量模型预测数据比较图和软测量模型预测误差量图,从图6~图7中可以看出热值软测量模型可以反映出热值的变化趋势,其预测误差量和相对误差量的变化范围为[-25, 25] kcal/m3和[-0.02, 0.02],能满足工业现场的应用要求。

图6 测试数据和软测量模型预测数据比较示意
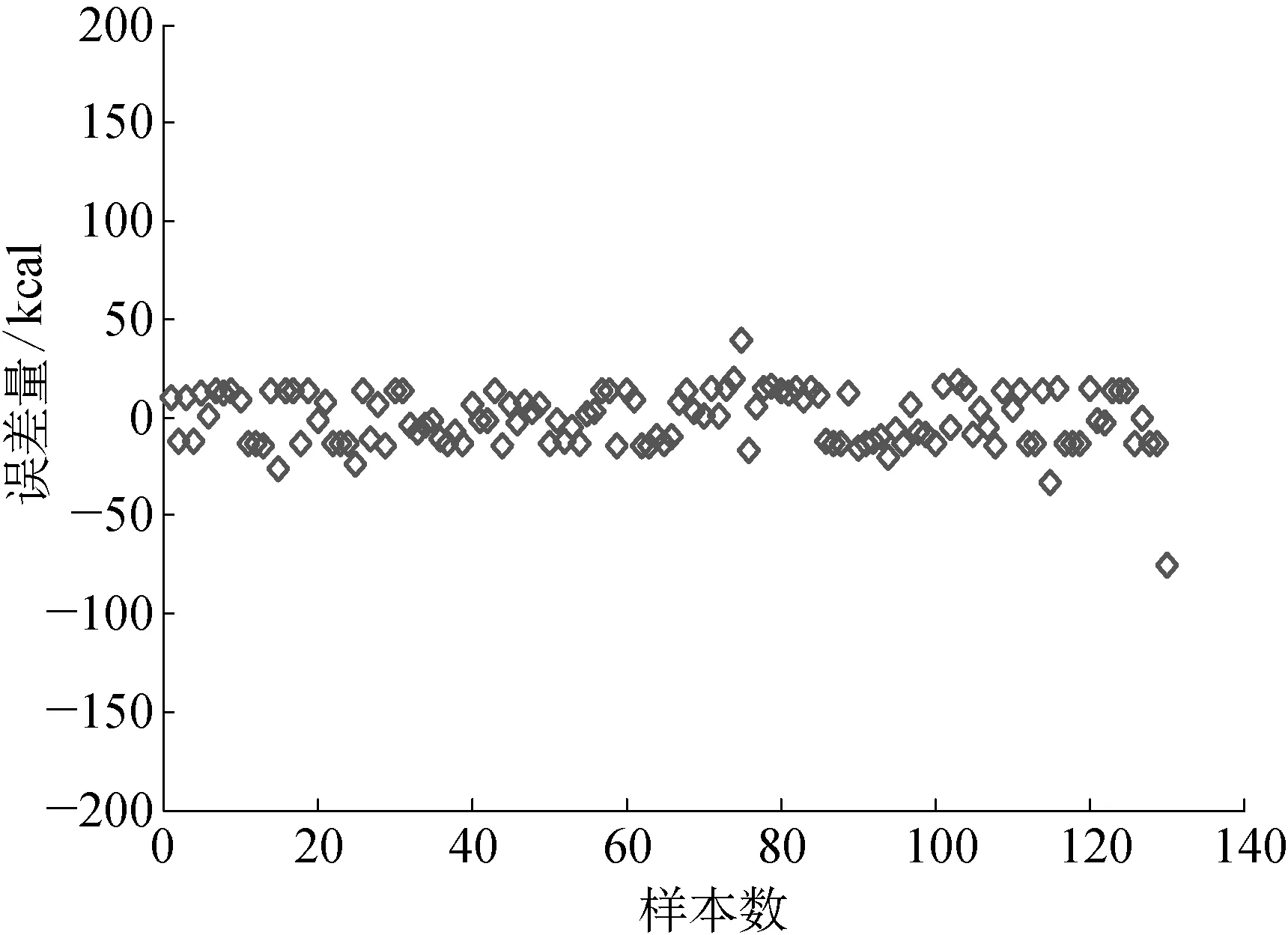
图7 软测量模型预测误差量示意
4 结束语
从仿真结果上可以看到,基于支持向量机的热值软测量模型,充分显示了燃料气系统热值的变化特征,其预测值误差的变化范围可以满足工业现场的应用要求。但在研究过程中也存在两个方面的问题需要解决。
1) 软测量模型的均方误差(MSE)和相关系数(R)只能达到0.010 56和82%,仍存在进一步优化的空间,如果采用新的优化算法如粒子群优化算法(PSO)和遗传算法(GA)优化模型参数c,g,可能会得到更好的预测效果。
2) 采用离线数据训练好的软测量模型,在运行一段时间后,随着工况的改变,其预测精度会出现一定程度的下降,为了使软测量模型能够适应新的工况,可在软测量模型中增加在线自校正环节,如增量式支持向量机算法解决该问题,并可进一步提升模型的泛化能力。
参考文献:
[1]王松汉.乙烯装置技术与运行[M].北京: 中国石化出版社,2009.
[2]杨思远,徐佩亮,王振雷.基于小波神经网络的热值软测量建模[J].石油化工自动化,2011,47(04): 34-37.
[3]刘漫丹,杜文莉,钱峰.裂解炉燃料气热值的模糊神经网络软测量[J].计算机集成制造系统-CIMS,2003,9(05): 412-416.
[4]张照娟.动态模糊神经网络的研究及在燃料气热值软测量中的应用[D].上海: 华东理工大学,2008.
[5]史峰,王小川,郁磊,等.MATLAB神经网络30个案例分析[M].北京: 北京航空航天大学出版社,2010.
[6]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(01): 32-42.
[7]孙优贤,褚健.工业过程控制技术(方法篇)[M].北京: 化学工业出版社,2005: 159-162.
[8]陈果,周伽.小样本数据的支持向量机回归模型参数及预测区间研究[J].计量学报,2008,29(01): 92-96.
[9]陈文杰,王晶.基于支持向量机的聚酯黏度在线软测量[J].控制工程,2005,12(05): 492-495.
[10]赵猛.在线分析仪表在乙烯装置中的应用[J].工业仪表与自动化装置,2009(06): 80-82.
[11]王瑞超,孙宇,胥小勇.基于模糊神经网络的薄膜收卷锥度张力控制系统[J].化工自动化及仪表,2013,40(03): 316-320,400.
[12]王云亮,崔学海.基于神经网络的谐波检测研究[J].化工自动化及仪表,2013,40(03): 330-333.
