基于WebGIS 的油田应急抢险最短路径算法研究
2014-09-10任伟建左方晨康朝海王琼霍凤财
任伟建,左方晨,康朝海,王琼,霍凤财
(东北石油大学 电气信息工程学院,黑龙江 大庆 163318)
网络分析作为网络地理信息系统(WebGIS)最主要的功能之一,是地理信息系统(GIS)的重要组成部分,在电子导航、交通旅游、城市规划、电力、通信等各种管网及管线的布局设计中发挥着重要的作用。而最短路径是WebGIS网络分析最基本、最关键的问题,在交通网络结构的分析、交通运输线路的选择、通信线路的建造与维护、运输货流的最小成本分析、城市公共交通网络的规划等方面,都有直接应用的价值[1]。
随着人们对安全、环境的重视以及油田突发事件的增多,油田应急系统的研究和应用越来越广泛。油田应急救援过程应能够及时、有效地将应急资源运送到事故现场,这就涉及最短路径问题。但在应急抢险的过程中,最短路径需要综合考虑路径的属性、资源运送的时效性、安全性、经济性等因素。为此,在抢险过程中,采用合适的最短路径搜索算法,尽量减少计算机的运算时间,是研究最短路径的一个重要方向[2]。
最短路径算法主要包括图论基本方法[3]、启发式搜索方法[4]、动态规划方法[5]、神经网络方法[6]等。启发式搜索方法多采用A*算法,但由于其执行时间通常为指数级,故一般较少采用;动态规划方法是一种解决多阶段决策问题的有效方法,但其动态决策过程中需要存储大量的阶段状态信息,故该算法目前主要适于普通小型试验级网络的最短路径处理;神经网络方法是一种新兴的算法,但由于其不成熟性,计算效率也较低,故较少采用;在实际过程中使用最多的是图论基本方法,其中较为常用的就是迪杰斯特拉(Dijkstra)算法。由于Dijkstra算法能适应网络拓扑的变化,性能稳定,因而在计算机网络拓扑路径选择以及WebGIS中得到了广泛的应用。目前在国内外有许多学者对Dijkstra算法进行了许多卓有成效的研究、改进和优化[7-9],其中有两种改进后算法的测试效果较好,分别是: DKA(the Dijkstra’s algorithm implemented with approximate buckets)和DKD(the Dijkstra’s algorithm implemented with double buckets),适合对2个节点间的最短路径问题进行求解。当面对大型的网络、对时效要求很高的问题时,这些算法的搜索效率会严重地降低,也不能满足问题解决的需要。笔者针对WebGIS网络分析中的最短路径问题,在Dijkstra算法的基础上,对其数据结构和计算方法作了一系列的改进,优化了系统的性能并采用面向对象的方式实现了该算法,算法效率得到了明显提高。
1 传统Dijkstra算法
Dijkstra算法是Dijkstra E W于1959年提出的一种按路径长度递增的次序产生最短路径的算法,被认为是解决单源点间最短路径问题比较经典而且有效的算法。其基本思想是生成1棵以固定起点为根的最短路径生成树[10]。根到树中每个节点的路径即为根到该点的最短路径,因为传统Dijkstra算法所求问题的网络中不存在负权,所以这棵最短路径生成树在生成过程中,将对各节点按其距固定起点的远近以及点间的邻接关系来逐个加入到树中,先近后远。
Dijkstra的表述通常有两种方式: 用永久和临时标号方式(Dijkstra算法也被称为标号作业法,通过不断地迭代产生出所有的永久标号);用OPEN,CLOSE表方式。文中采用的是永久和临时标号方式,算法的过程如下[11,16]:
设G=(V,E)是1个带权值有向图(这里权值可以是长度,也可以是时间、费用等),把图中节点集合V分成2组: 第1组为已求出最短路径的节点集合(用S表示,初始时S中只有1个起始节点,以后每求得1条最短路径,就将其加入到节点集合S中,直到全部节点都加入到S中,算法结束);第2组为剩余的还没确定的最短路径节点的集合(用U来表示),依据最短路径长度的递增顺序把第2组中的节点依次地加入到集合S中。在加入的过程中,总保持从起始节点v到S中各个节点的最短路径的长度不大于从起始节点v到U中任何节点的最短路径的长度。此外,每一个节点都对应着一个长度,S中节点的长度就是从v到此节点的最短路径的距离;U中节点的长度,是从v到此节点只包括S中的节点为中间节点的当前最短路径长度。
1.1 Dijkstra算法的标号
对图中的某点vj赋予2个标号(l,k),第1个标号l表示从起点v0到vj最短路径的长度;第2个标号k表示在v0到vj的最短路径上的vj前面1个邻点的下标,从而找到起点v0到终点的最短路径及v0到终点vt的距离。算法的基本步骤如下:
1) 给起点v0以标号(0,k),表示v0到v0的距离为0,v0为起点。
2) 找出已标号的点的集合S,未标号的点的集合U以及弧的集合{(vm,vn)|vm∈S,vn∈U}(m,n∈j),这里弧的集合是指所有从已标号的点到未标号的点的弧的集合,其中vm表示已经标号的节点,vn表示与vm相邻未标号的节点。
3) 如果{(vm,vn)|vm∈S,vn∈U}是空集,则计算结束。如果终点vt已标号(l,k),则v0到终点vt的距离为l,而从v0到vt的最短路径,则可以从vt反向追踪到起点v0而得到。如果上述集合不是空集则转下一步。
4) 对于上述集合中的每一条弧,计算sm n=l+cm n(cm n表示已标号节点vm到未标号节点vn的距离),在所有sm n中,找到其值为最小的弧。则给此段弧的终点v标以双标号(sm n,k),返回步骤2),以此类推。
若在步骤4)中,使得sm n值为最小的弧有多条,则这些弧的终点既可以任选1个标定,也可以都予以标定,若这些弧中有些弧的终点为同1点,则此点应有多个双标号,以便最后可找到多条最短路径。
1.2 Dijkstra算法的应用
例如求图1中v0到v3的最短路径:
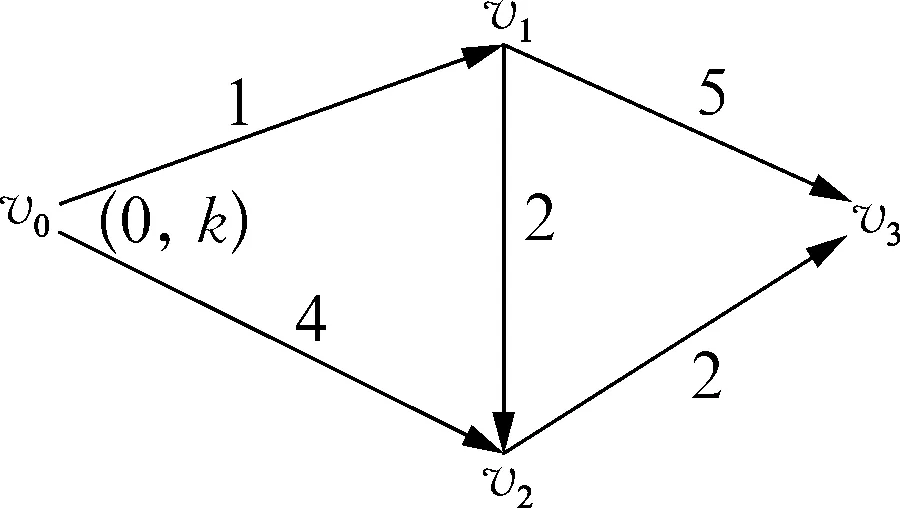
图1 Dijkstra算法示意
1) 给起点v0以标号(0,k),表示v0到v0的距离为0,v0为起点。
2) 找出已标记节点S={v0},未标号点的集合U={v1,v2,v3}以及弧的集合{(vm,vn)|vm∈S,vn∈U}={(v0,v1),(v0,v2)}。
s01=l0+c01=0+1=1
s02=l0+c02=0+4=4
Min(s01,s02)=s01=1
这样给弧(v0,v1)的终点v1标以(1, 0),表示v0到v1的距离为1,并且在v0到v1的最短路径中v1前面的1个点是v0。
3) 此时S={v0,v1},U={v2,v3},弧集合{(vm,vn)|vm∈S,vn∈U}={(v0,v2), (v1,v2), (v1,v3)}。
s02=l0+c02=0+4=4
s12=l1+c12=1+2=3
s13=l1+c13=1+5=6
Min(s02,s12,s13)=s12=3
这样给弧(v1,v2)的终点v2标以(3, 1),表示v0到v2的最短距离为3,并且在v0到v2的最短路径中v2前面的1个点是v1。
4) 这时S={v0,v1,v2},U={v3},弧集合{(vm,vn)|vm∈S,vn∈U}={(v1,v3), (v2,v3)}。
s13=l1+c13=1+5=6
s23=l2+c23=3+2=5
Min(s13,s23)=s23=5
这样给弧(v2,v3)的终点v3标以(5, 2),表示v0到v3的最短距离为5,并且在v0到v3的最短路径中v3前面的1个点是v2。
5) 这时S={v0,v1,v2,v3},弧集合{(vm,vn)|vm∈S,vn∈U}=φ,计算完成,如图2所示。

图2 Dijkstra算法标号示意
根据v3的标号可得v0到v3的距离是5,最短路径为v0—v1—v2—v3。
按标记法实现Dijkstra算法的过程中,核心步骤就是从未标记的点中选择1个权值最小的弧段,即1.1节所述算法的2)~4)。这是一个循环比较的过程,如果不采用任何技巧,未标记点将以无序的形式存放在1个链表或数组中。那么要选择1个权值最小的弧段就必须把所有的点都扫描一遍,在大数据量的情况下,这无疑是制约计算速度的瓶颈。
2 Dijkstra算法的优化
Dijkstra算法是目前大多数系统解决最短路径问题的基础。Dijkstra算法的优点是程序设计简单、通用性强,但不是专门针对特定2个点的,而在WebGIS中,往往是寻找2个特定点间的最短路径,此时Dijkstra算法的效率会降低,而且Dijkstra算法采用的邻接数据矩阵结构,占用空间十分巨大,严重浪费了计算机的资源,影响计算速度,不适合WebGIS节点量巨大的实际情况。因此在WebGIS应用中,对Dijkstra算法的改进是十分必要的。笔者从WebGIS的存储空间以及算法的本身出发对Dijkstra算法提出了优化和改进,使之更适合WebGIS中针对固定2个点间最短路径的实际情况。
2.1 WebGIS存储空间的优化
最短路径优化研究应尽量减少算法占用的存储空间。WebGIS中的数据(如道路、管网、线路等)要进行最短路径的计算,就必须将其按节点和边的关系抽象为图的结构,这在WebGIS中称为构建网络的拓扑关系(这里的拓扑关系仅记录了线与节点的关系而无线与面的关系,是不完备的拓扑关系)[12]。对于图3所示的电子地图,要计算图中2个点间的最短路径,需将图3中道路抽象为具有拓扑结构的道路网络,如图4所示。
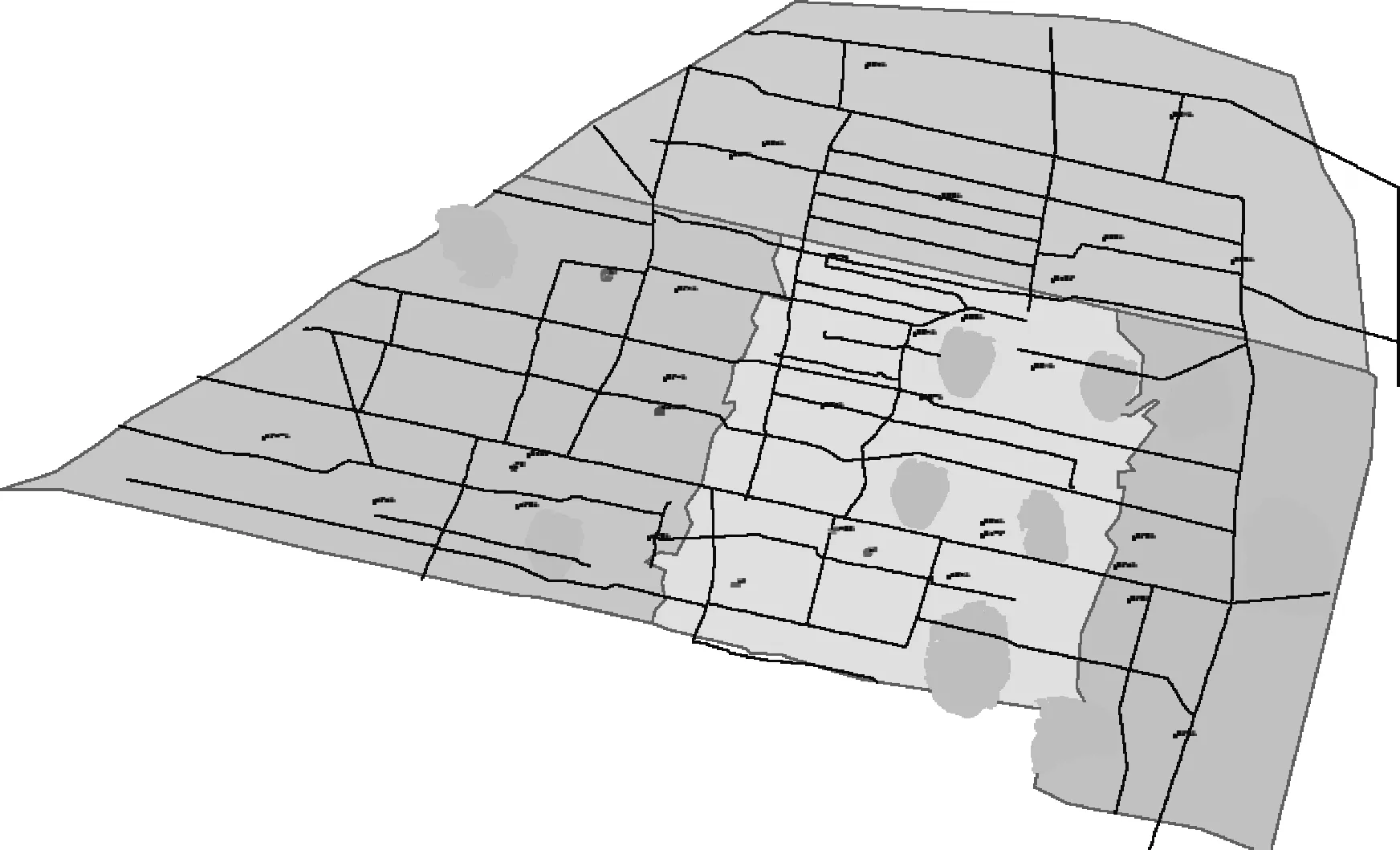
图3 电子地图示意
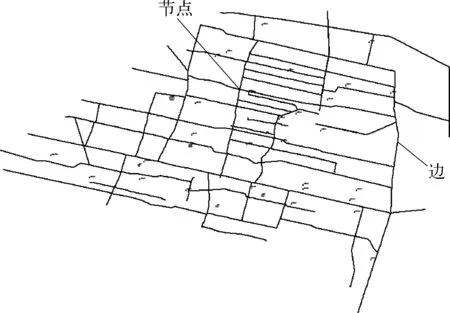
图4 拓扑结构的道路网络示意
具有拓扑结构的道路网络由节点、边及相应的拓扑关系构成。其中节点是道路的交叉点、端点,边是2个点间的一段道路。在网络分析过程中,实际只需关心网络边的信息,如边的权值、起点、终点,就可采用只存储边的网络拓扑信息,不存储实际节点的拓扑信息,减少空间分析时所要检索的数据量。
另外对节点和弧段等数据采取动态管理的策略,也会减少算法占用的存储空间。所谓动态管理,是指算法的开始,并不是创建整个网络中的节点和弧段的数据结构,而是根据算法运行的需要,动态地生成、扩展以及删除相应的节点。对数据实行动态管理的策略,能够最大限度地发挥存储空间的利用效率,避免无效数据占用大量的存储空间。
2.2 直线法优化Dijkstra算法
直线法优化Dijkstra算法是指通过减小算法中的搜索范围,以尽快达到目标节点。其核心思想: 在把研究的网络看成平面网络的前提下,将临时标记节点到源点的最短路径与该临时标记节点到目标节点的直线距离之和,作为此临时标记节点的一个属性值,即选取此属性值最小的临时节点作为永久标记节点,这种优化算法称为直线优化算法。此方法使得Dijkstra算法的搜索方向智能地趋向目标节点,减少了算法中遍历的节点个数,从而提高了搜索速度。
受直线优化算法的启发,结合WebGIS的数据组织方法可以采取一种优先搜索的方法。 从几何的知识可知2个点之间直线距离最短,在错综复杂的道路网上,任选2个点,其最短路径可设为1条从起点到终点的直线,该直线作为1条道路存在的可能性很小,但该线代表着1条路线的趋势,顺着这个方向的某条路径是起点到终点的最短路径的可能性极大。
如图5所示,求A点到E点的最短路径,可以在AE间虚拟一条连接2个点的直线,然后比较A点到邻接点间的路段与此虚拟直线的夹角,找出夹角最小的1条AB优先处理;接下来以B点代替A,以B为起点,以同样的方法找出与BE夹角最小的路段BF优先处理;接着以F点代替B点,以F点为起点,以同样的方法找出与FE夹角最小的路段FI优先处理。以此类推,最终找出1条最短路径。
由上可知,改进后的算法是在起点和终点间建立树状网络拓扑的过程,同时也是路径搜索的过程,只是在搜索过程中采用了一定的技巧,将未搜索的路径以有方向、有目的的形式进行,从而降低原算法中搜索那些与终点背道而驰的路径而导致算法效率低下的问题,大幅提高了计算机的运行速度。
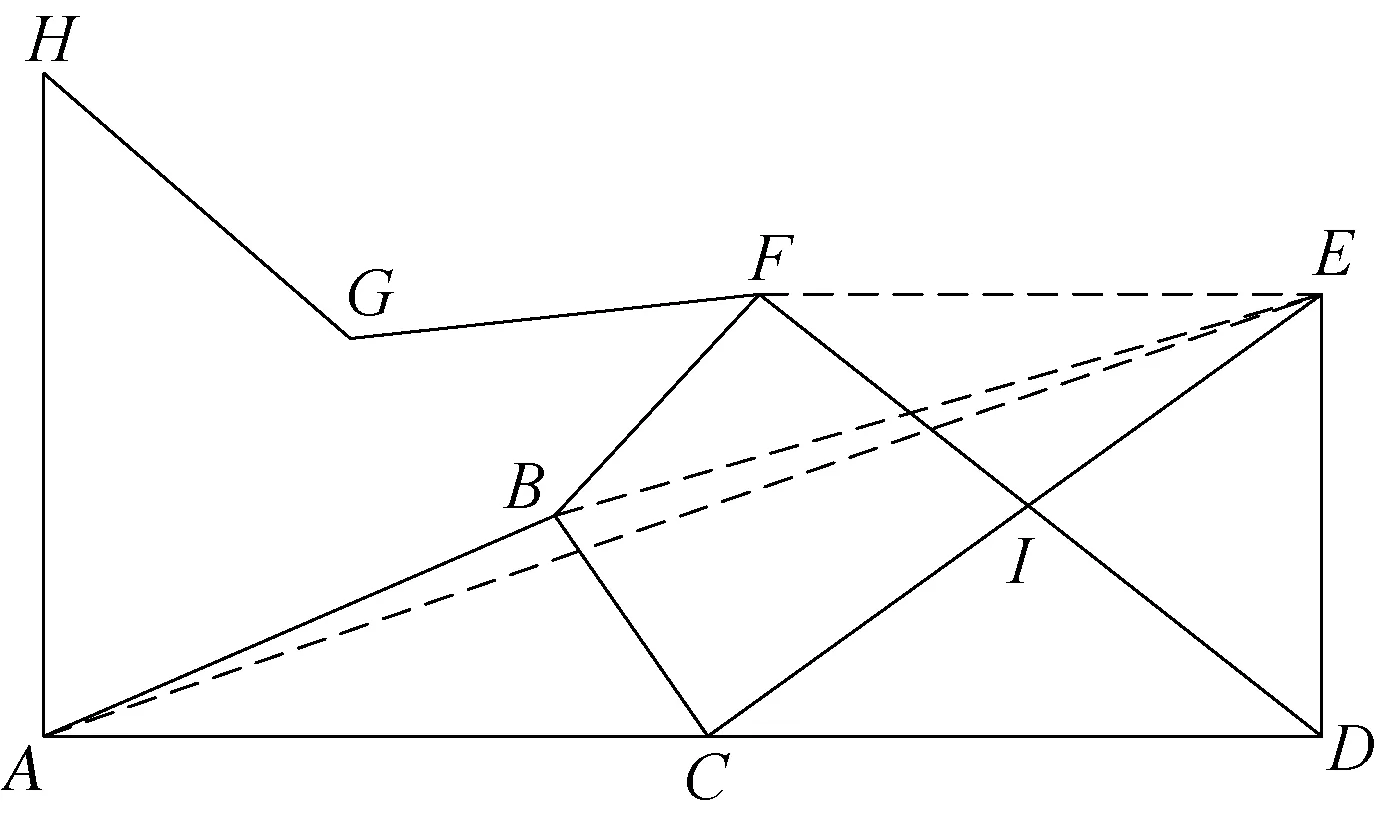
图5 直线优化算法路径示意
3 改进后的Dijkstra算法在油田应急抢险系统中的应用
油田应急抢险系统是集GIS、数据库、多媒体、语音技术及现代通信技术为一体的多功能辅助决策系统,是WebGIS空间分析的一个重要方向[13-15]。系统主要功能: 利用该系统的空间查询技术确定事故发生地点,快速显示采油厂的电子地图和地理信息,在电子地图上显示各主要功能单位(如119,110,120和物资储备库)到事故发生地点的最佳行驶路线。
该系统利用ArcGIS Server 9.3 组件,在Visual C#下实现最佳路径的查询功能,针对油田道路网络的具体情况,完成了改进后的Dijkstra算法在油田应急抢险系统中的应用,实现了单目标点—多源点最佳路径查询工作。该道路网中共有258个节点,221段弧,在主频为3.40 GHz、内存2G的计算机中,计算5条总长度为15 667 m路径,耗时约1.375 s。
用不同的道路数据,在同一台电脑上,笔者又多次模拟求解同样起点到终点的距离,表1显示了该算法和Dijkstra算法的运行时间结果对照。
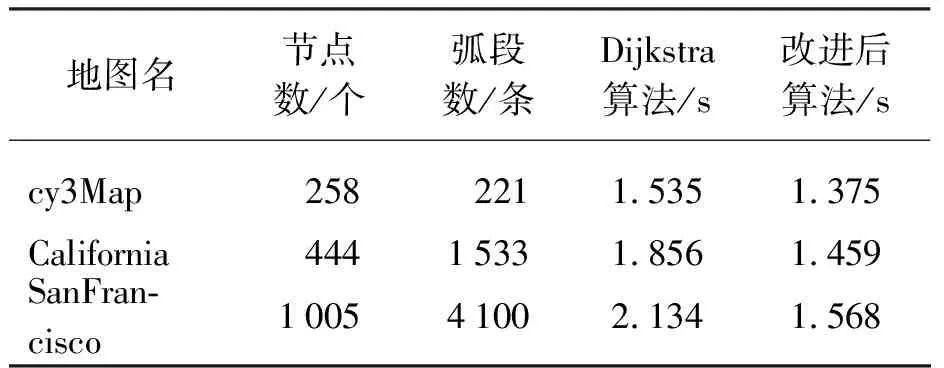
表1 同样起点到终点运行时间对比
从表1可以看出,当网络节点数较少时,两种算法的运算时间相差不多,效率差异不明显;但随着网络中节点数目的增多,Dijkstra算法需要遍历图中所有的节点,效率会降低,而该算法按照一定的搜索方向,减少了搜索节点的个数,提高了搜索速度,完全满足了油田应急抢险系统所要求的最佳时间(1~2 s)。
4 结束语
文中详细地介绍了Dijkstra算法的基本原理,并且结合WebGIS的实际情况,对原有的算法提出了优化方法。既节省了存储空间,又提高了运行效率,使得Dijkstra算法真正地应用到油田应急抢险系统中。然而,目前道路网越来越复杂,也越来越庞大,在应用过程中必须要考虑众多因素,如道路拥挤程度、道路等级、交叉口的延误时间、交通管制信息等,因而寻找考虑多种因素的最优应急抢险路径,将是需要进一步研究的问题。
参考文献:
[1]PALLOTLINO S. Shortest Path Methods: Complexity, Interrelation and New Propositions. Networks[J]. 1984, 14(02): 257-267.
[2]王一军,罗大庸,张航.城市应急最优路径算法[J].系统工程,2008,26(07): 86-91.
[3]唐文武,施晓东,朱大奎.GIS中使用改进的Dijkstra算法实现最短路径的计算[J].中国图象图形学报,2000,5(12): 1019-1023.
[4]魏唯,欧阳丹彤,吕帅,等.一种多目标增量启发式搜索算法[J].吉林大学学报,2009,47(04): 752-758.
[5]赵慧娟,汤兵勇,张云.基于动态规划法的物流配送路径的随机选择[J].计算机应用及软件,2013,4(30): 110-112.
[6]纪其进.一种基于脉冲耦合神经网络的最短路径算法[J].小型微型计算机系统,2005,26(05): 826-829.
[7]ZHAN F B. Three Fastest Shortest Path Algorithms on Real Road Networks[J]. Journal of Geographic Information and Decision Analysis, 1997,1(01): 69-82.
[8]熊碧霞,杨春兰.基于Dijkstra算法的最短时延路由算法的实现[J].中国水运,2009,9(02): 98-99.
[9]陈灵敏.最短路径算法在高速公路联网收费中的研究及应用[M].贵州大学学报(自然科学版),2009,26(01): 47-50.
[10]GILLES B, PAUL B. Fundamentals of Algorithmics(算法基础)[M].邱仲潘,柯渝,徐峰,等,译.北京: 清华大学出版社,2005: 154-157.
[11]胡洪林.求最短路径的Dijkstra算法原理分析[J].计算机科学,2008,34(07): 60-74.
[12]王陵,段江涛,王保保.GIS中最短路径的算法研究与仿真[J].计算机仿真,2005,22(01): 117-120.
[13]姜凤辉,李树军,姜凤娇.基于GIS的Dijkstra改进算法及其在交通导航系统中的应用[J].测绘与空间地理信息,2011,34(04): 129-131.
[14]高晓荣,徐英卓.油田事故应急救援可视化决策支持系统[J].计算机工程,2010,36(15): 236-239.
[15]羌龙华.基于GIS的油田应急指挥系统的设计与实现[J].自动化技术与应用,2011,30(07): 38-41.
[16]SCHULZ F,WAGNER D,WEIHE K. Dijkstra’s Algorithm Online: An Empirical Case Study From Public Railroad Transport[J].Journal of Experimental Algorithmics,2000(05): 110-123.
[17]宋士祥,张强,吴明,等.基于GIS和SOA的长输管道管理系统的设计与实现[J].化工自动化及仪表,2012,39(08): 998-1000,1033.
