电气几何模型的分析计算

刘磊

(中国华电工程(集团)有限公司， 北京 100035)

1 问题的提出

在电力系统的跳闸停电事故中，雷击电网引起的事故占有很大比重。据统计，因雷击线路造成的跳闸事故约占电网总事故的60%以上[1]。在我国110～220 kV输电线路的各种雷击事故中，线路绕击跳闸率超过了总雷击跳闸率的半数以上。国外735～765 kV的超高压线路运行经验同样表明，绕击跳闸是超高压线路雷击跳闸的主要原因[2]。因此，在工程实际中，绕击跳闸率的准确评价和分析具有重要的意义。目前，线路绕击率的计算使用较多的方法为规程法[3]和电气几何模型法[4-5]。其中，规程法指的是雷电绕击的分析与计算，它以我国电力行业标准为依据，分平原和山区2种情况，给出了保护角与杆塔高度有关的经验公式来计算绕击率。电气几何模型(EGM)是以“闪击距离”(击距)的概念为基础对线路的绕击机制进行分析和计算的，击距指的是雷电先导头部与地面目标的临界击穿距离。规程法给出的绕击率计算公式的特点是简单且实用性强，但其公式是建立在多年的运行数据统计及小电流试验的基础之上，试验模型及数据与现有的输电线路并不完全相符，而且统计数据具有很大的平均性，计算和分析的准确性较低。电气几何模型将特定线路具体的结构尺寸与线路的耐雷水平结合在一起，其分析过程反映了具体线路的特点，对于线路屏蔽失效及高杆塔而言，采用负保护角等现象的解释具有较高的合理性，因而采用电气几何模型对线路绕击率进行计算分析，其准确性更高。

2 电气几何模型的基本思想

从地闪放电的机制来分析，雷电下行先导的发展具有一定的分散性和随机性。当下行先导离地面物体较远时，雷击点无法确定。只有当下行先导与被击物在一定距离之内时，雷击点的选择性才会表现出来。电气几何模型以闪击距离(击距)的概念为基础，用击距表示地面不同物体对雷电下行先导的吸引能力。所谓击距就是雷云下行先导对地面物的临界击穿距离，电气几何模型理论认为，雷云下行先导先到达哪个地面物的击距之内，该物体即为雷击点。

电气几何模型的基础是击距，当不同地面物的击距确定以后，就可以通过几何分析法来对线路的绕击情况进行分析，图1给出了用电气几何模型法对输电线进行绕击计算时的基本原理。

图1 电气几何模型分析绕击概率原理图

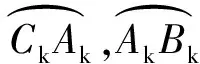
线路绕击跳闸率(每年雷击次数/100 km)

(1)

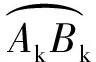
3 电气几何模型的计算方法

式(1)给出了线路绕击跳闸率的计算公式，式中参数与雷电流及线路的结构尺寸有关，在计算出式(1)中的各个参数之后，线路的绕击跳闸率即可得到求解。下面对各参数的计算公式进行分析。

3.1 击距公式

击距是电气几何模型的基础，不同研究者给出了不同的计算公式，本文在计算线路绕击跳闸率时，采用1993年IEEE导则中推荐的击距公式，即

rs=8I0.65。

(2)

3.2 击距系数

式(2)中击距只与雷电流幅值有关，而研究表明，击距与地面物的结构也有关系，这一结构主要指地面物体的高度。当杆塔高度不同时，大地与线路对雷电先导的吸引能力显然相同，即击距应该不同。研究者提出用击距系数来表示高度不同对击距的影响，击距系数定义为大地击距与导线击距的比值。本文采用了1997年IEEE规程中推荐的击距系数计算公式

k=0.36+0.17ln(43-Hd)，Hd≤40 m ，

(3)

k=0.55，Hd>40 m 。

(4)

3.3 落雷密度

本文采用IEEE导则中推荐的落雷密度(每年雷击次数/km2)公式，即

Ng=0.04Td1.25。

(5)

Td一般取40雷电日/年，此时计算可得Ng=4.024(每年雷击次数/km2)。

3.4 雷电流概率密度函数

雷电流的概率密度函数采用参考文献[8]给出的方法，参考文献[8]根据欧美的观测结果，统计得出雷电流的幅值服从对数正态分布，本文计算雷电流幅值概率密度的函数为

(6)

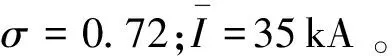
3.5 暴露距离的分类计算

由电气几何模型的原理分析可知，暴露距离与避雷线、导线、大地三者引雷曲线的交点有关。如图2所示，设三者引雷曲线相交于A，B2点，利用暴露距离来分析计算线路绕击跳闸率的前提是，假设雷电先导的发展方向是垂直向下的，因此，当线路结构不同造成A，B2点相对位置不同时，暴露距离的计算将会出现不同的情况，电气几何模型坐标如图2所示。

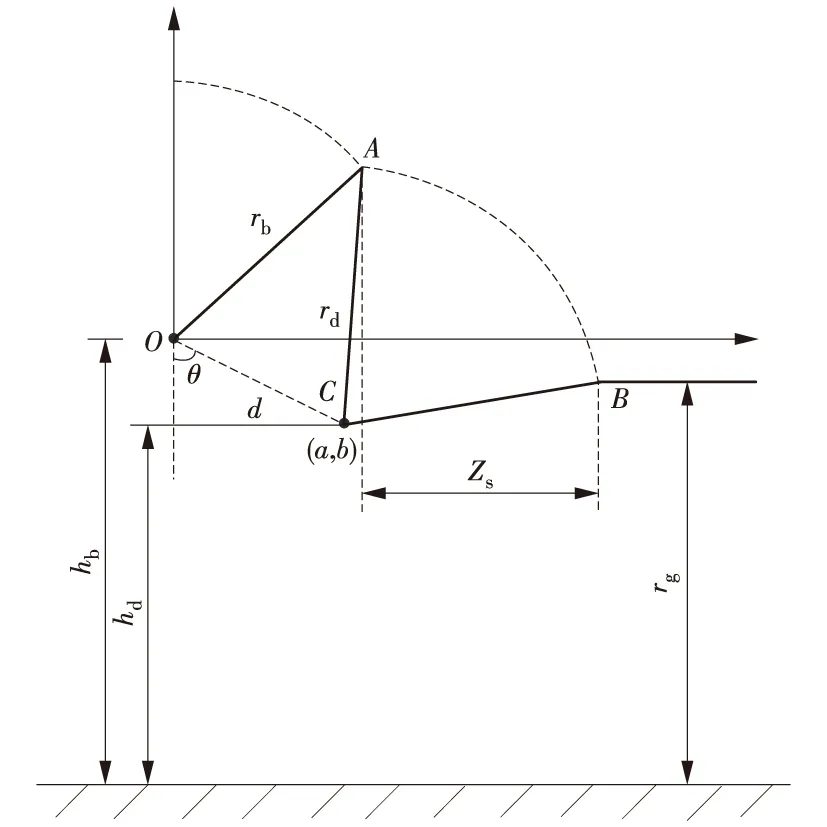
图2 电气几何模型坐标图

由图2可知，A点为避雷线引雷弧段与输电线路引雷弧段的交点。在图2中，以避雷线为坐标原点(O)建立坐标系。C点为输电线路，其坐标为(a，b)，根据2个圆相交列出方程组(7)，可得到A点的坐标(xA，yA)。

(7)

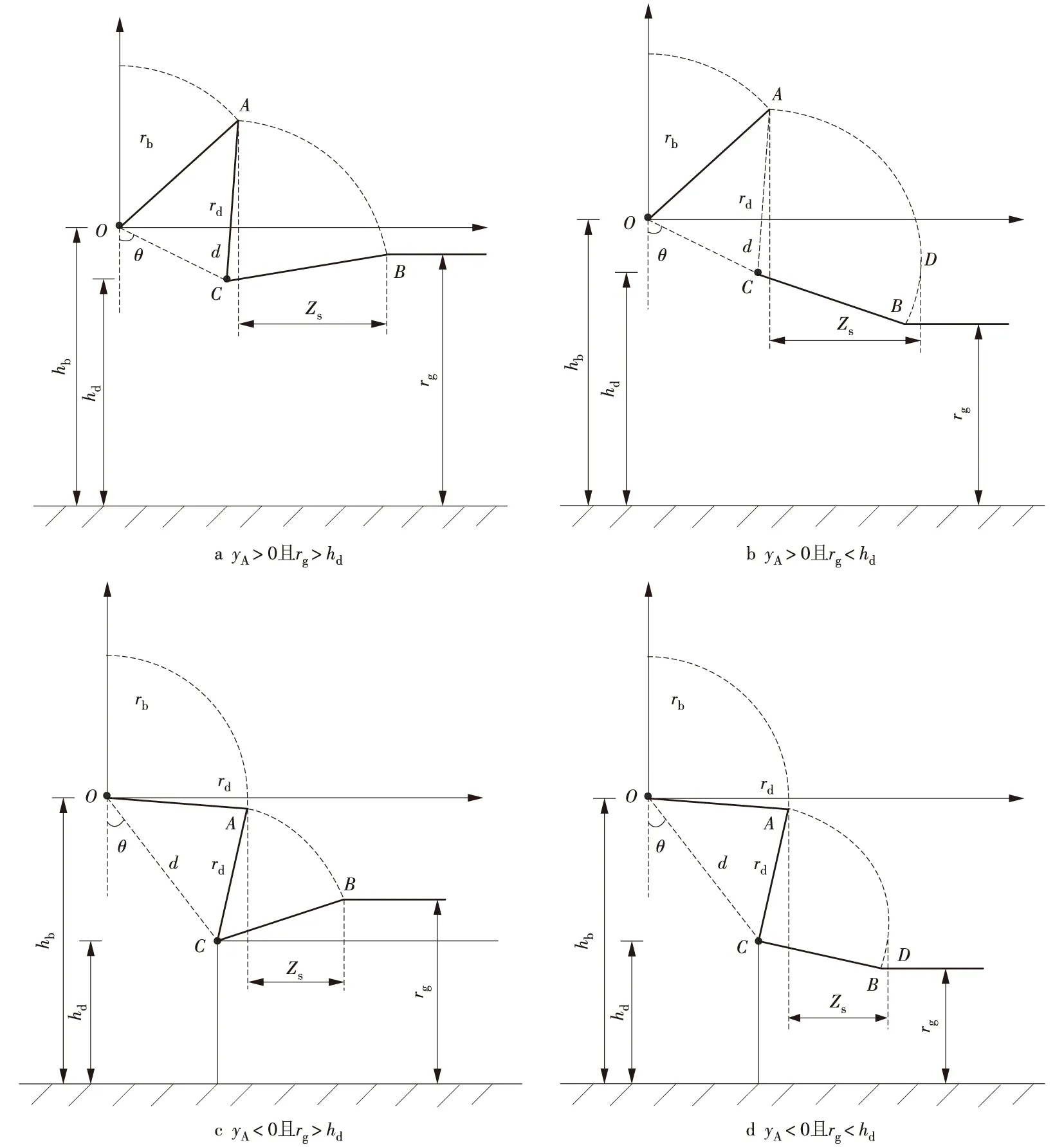
图3 电气几何模型屏蔽示意图

笔者认为式中避雷线击距rb和导线击距rd相等，即rb=rd。

B点为输电线路引雷弧段与地面引雷直线的交点，解下列方程组得B点的坐标(xB，yB)。

(8)

解方程组(7)，(8)，可得到A，B点的坐标为

(9)

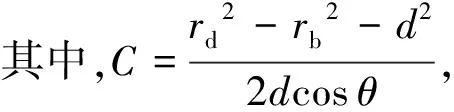
(10)

当A，B2点相对位置不同时，暴露距离的计算可分为以下几种情况。

(1)若实际避雷线与导线的屏蔽几何关系满足2个圆的交点A存在，yA>0且rg>hd，如图3a所示，则

Zs=xB-xA。

(11)

(2)若实际避雷线与导线的屏蔽几何关系满足2个圆的交点A存在，yA>0且rg

Zs=xD-xA，

(12)

其中，xD=dsinθ+rd。

(3)若实际避雷线与导线的屏蔽几何关系满足2个圆的交点A存在，yA<0且rg>hd，如图3c所示，则

Zs=xB-rb。

(13)

(4)若实际避雷线与导线的屏蔽几何关系满足2个圆的交点A存在，yA<0且rg

Zs=xD-rb。

(14)

3.6 雷电流上、下限值

(1)临界雷电流。线路的绕击耐雷水平就是其发生绕击跳闸的临界雷电流Ie。绕击耐雷水平取决于线路绝缘状况，当线路绝缘子串的50%闪络电压 已知时，可由式(6)对其进行求解。

(15)

式中：Zd为输电线路等值波阻抗，参考文献[3]取Zd=400 Ω对耐雷水平进行估算。

(2)临界最大雷电流。由电气几何模型的原理可知，最大击距对应的雷电流即为发生绕击的临界最大雷电流Imax。最大临界雷电流可通过最大击距与击距公式进行求解。当线路暴露距离为0时，对应的击距最大。根据暴露距离的计算公式可求得最大击距rmax为

cosθ/(2F) ，

(16)

式中：F=K2-sinθ；G=F[(hc+hb)/cosθ]2；θ为避雷线保护角；k为击距系数。

4 计算实例

通过上述电气几何模型法的基本原理及其计算过程的详细分析，可对线路的绕击跳闸率进行计算。某一实际220 kV线路，其基杆塔的参数见表1，本文利用电气几何模型法(EGM)与规程法对其绕击情况进行计算与对比分析。该线路2000—2001平均落雷密度为0.0139 82(每年雷击次数/km2)，不考虑地面倾角。规程法中，平原地区绕击率的计算公式为

(17)

式中：Pα为绕击率；α为保护角；hgt为杆塔高度。

不计击距系数的计算结果见表2。

表1 线路参数类型 m

注：在U50%电压为1 200 kV的条件下。

表2 不计击距系数的计算结果

由表2可以看出, 规程法计算的线路绕击跳闸率非常低，而利用EGM计算的绕击跳闸率较大，从运行统计的数据来看，电气几何模型的计算结果更加符合实际情况。对于本文论述的电气几何模型法考虑线路的实际结构，结果更加准确。

5 结论

运用电气几何模型法对线路绕击进行分析计算具有较高的准确性。本文在介绍电气几何模型法的基础上，给出了运用电气几何模型法分析计算线路绕击跳闸率的详细过程，并对不同电气几何结构下的暴露距离进行了分类讨论，给出了不同情况下暴露距离的计算公式。在此基础上，运用电气几何模型法和规程法，对某线路其中的两基杆塔进行了绕击计算，对比分析了2种方法计算结果。规程法计算的绕击率非常小，而电气几何模型法的计算结果较大且更符合实际情况。

参考文献：

[1]林福昌.高电压技术[M].北京：中国电力出版社，2011.

[2]李晓岚，尹小根，余仁山，等.基于改进电气几何模型的绕击跳闸率的计算[J].高电压技术，2006，32(3)：42-42.

[3]DL/T 620—1997 交流电气装置的过电压保护和绝缘配合[S].

[4]张志劲，司马文霞，蒋兴良，等.超/特高压输电线路雷电绕击防护性能研究[J].中国电机工程学报,2005，25(10)：1-6.

[5]李晓岚.击距系数及基于电气几何模型的输电线路绕击跳闸率计算的研究[D].武汉：华中科技大学，2005.

[6]IEEE working group on estimting lightning performance of transmission lines，estimating lightning performance of transmission linesⅡ-updates to analytical models[J].IEEE Transactions on Power Delivery，1993，8(3)：1254-1267.

[7]韩孚昌，李晓岚. 基于电气几何模型的四种输电线路绕击跳闸率计算方法的比较[J].市场周刊:理论研究，2008，(1)：133-135.

[8]1243—1997 IEEE guide for improving the lightning performance of transmission lines[S].