基于SSSC的电网潮流计算
2014-09-10赵丽娜
赵丽娜
(广东省输变电工程公司 咨询分公司,广州 510160)
0 引言
静止同步串联补偿器(SSSC)是近年来电力系统出现的FACTS控制器的一种。它与输电系统以串联方式联结,是应用可关断晶闸管(GTO)构成的同步电压源的控制器,基本原理是向线路注入1个与其电流相位相差90°的可控电压,等效为能快速控制线路的有效阻抗,从而进行有效的系统控制。
1 基于功率注入法的SSSC模型
功率注入法实际上是一种网络拓扑变换,它将线路上可调变量对系统的贡献移植到对应线路的两侧节点上,这样可在不修改原来节点导纳阵的情况下嵌入FACTS模型,最大限度地利用传统潮流计算中雅可比矩阵形成的公式和经验。结合功率注入法得到SSSC的等效注入功率模型如图1所示。
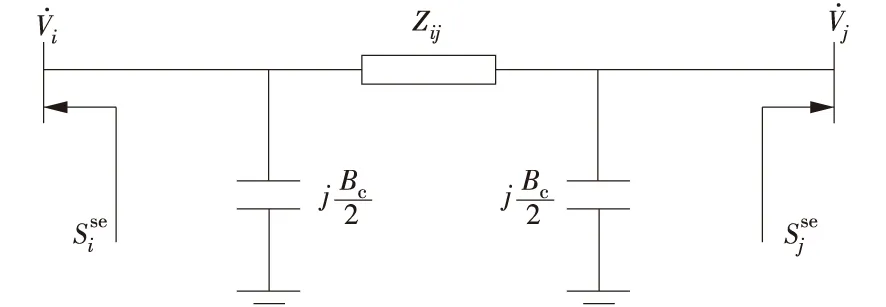
图1 SSSC的等效注入功率模型
根据功率注入法,SSSC潮流模型可以表示为
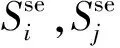
jBij+jBc/2)]*,
(2)
(Gij+jBij)]*,
(3)
Sij=Pij+jQij=Vi∠θi[(Vi∠θi+Vse∠δse-
Vj∠θj)*(Gij+jBij)*-j(Vi∠θi+
Vse∠δse)*Bc/2]。
(4)
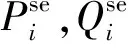
由式(2)~(4)可得
Bc/2)sin(θi-δse)] ,
(5)
Bc/2)cos(θi-δse)] ,
(6)
Bijsin(θj-δse)] ,
(7)
Bijcos(θj-δse)] ,
(8)
Pij=Vi2Gij-ViVj[Gijcosθij+
(Bij+Bc/2)sinθij]+
ViVse[Gijcos(θi-δse)+
(Bij+Bc/2)sin(θi-δse)] ,
(9)
Qij=-Vi2(Bij+Bc/2)-
ViVj(Gijsinθij-cosθij)+
ViVse[Gijsin(θi-δse)-
(Bij+Bc/2)cos(θi-δse)] 。
(10)
为了维持恒定的直流电压,SSSC与交流系统的有功交换必须为零,即
Pex=Re{VseI*}=0 ,
(11)
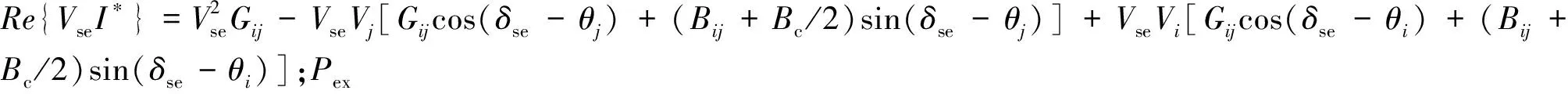
这样,通过功率注入法就可以把SSSC的模型加入到潮流计算模型中,不仅简化了潮流模型,而且可以与以往的潮流计算软件衔接,在无需对原有潮流计算软件做太大改变的情况下,计算出SSSC对功率分配的影响。
2 牛顿-拉夫逊法对SSSC雅可比方程的修改
计及SSSC的潮流计算,可描述为对下列方程组的求解:
(12)
式中:X为包含节点电压及相角的传统潮流方程的状态向量;Xu为包含SSSC注入电压幅值及相角的状态向量;方程组(12)为计及SSSC的节点功率平衡方程;方程组(12)中必须修正与SSSC相连节点的节点注入功率方程。
方程组(12)可由式(13)和式(14)表示。式(13)为与SSSC没有相连的节点的功率平衡方程。
式中:PGi,PLi分别为i节点发出有功功率和线路有功损耗;QGi,QLi分别为i节点发出无功功率和线路无功损耗。
对PQ节点来说,PGi,QGi,PLi,QLi为给定值,Vi,θi为待求变量。
对PV节点来说,PGi,PLi,Vi为给定值,QGi,PLi,θi为待求变量。
式(14)为与SSSC相连的节点的功率平衡方程。节点i,j为PQ节点,加上还要考虑SSSC对节点i,j的附加注入功率,此时节点i,j的功率平衡方程为
(14)
方程组(12)为SSSC的控制目标方程及约束方程,其中,SSSC的自身约束方程见式(10),SSSC的控制目标方程为
(15)
式中:Pijs,Qijs是线路ij有功功率和无功功率的给定值,即线路潮流SSSC的控制目标;Pij,Qij为Sij的有功和无功功率分量。则用牛顿-拉夫逊法联立求解方程组(12),雅可比矩阵为
(16)
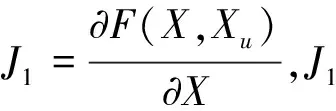
3 算例分析
为验证本文所提模型及算法的有效性,在IEEE-30节点系统上进行了分析计算:分别计算在IEEE-30节点系统不同支路上安装SSSC时和在同一支路上安装SSSC但支路潮流控制目标不同时线路中的潮流分布。
根据IEEE-30节点电力系统模型的网络结构和网络参数,该网络包括6台发电机(节点1,2,5,8,11,13,其中1为平衡节点,2,5,8,11,13为PV节点),21条负荷母线及43条支路,其中4条支路(6,9),(6,10),(4,12),(27,28)为变压器支路分别对应T1,T2,T3,T4。此时参数控制的约束条件为:0.9≤Vi≤1.1,0≤Vse≤1.0,-180°≤δse≤180°。 表1给出了在IEEE-30节点系统中支路4-6和支路21-22以及支路27-29上安装静止同步串联补偿器的情况,即分别在不同支路上装设SSSC时的潮流计算。SSSC分别装设在支路4-6节点4的出口处、支路21-22节点21的出口处以及支路27-29节点27的出口处。其中,4-6支路潮流的控制目标为7.95-4.80i,21-22支路潮流的控制目标为1.53-1.67i,27-29支路潮流的控制目标为-6.3+1.65i。由表1可以看出:系统中计入SSSC后,其各节点的电压水平明显改善且没有超出所给范围,SSSC控制变量的收敛值也在要求范围之内;系统计入SSSC后,给定的支路潮流控制目标也达到了,这验证了SSSC对支路潮流的控制作用。只是计入SSSC后的潮流计算迭代次数稍有增加,应进一步考虑如何减少潮流计算的迭代次数。
表2为IEEE-30节点系统中支路4-6上安装SSSC时不同控制目标下的潮流计算结果,方式1为没有安装SSSC,此时支路潮流为7.879-4.740 5i,方式2中4-6支路潮流控制目标为7.95-4.80i,方式3中4-6支路潮流控制目标为7.75-4.70i。由表2中数据可以看出,SSSC具有很强的潮流控制功能,且所得潮流结果均在给定范围内。方式2中通过SSSC的调节,线路传输的有功功率增加,其注入电压相角为正值,此时SSSC工作在容性模式下,它相当于在线路中串入1个电容,减小了线路阻抗,所以增大了线路传输有功功率;方式3和方式2正好相反,它通过SSSC调节使线路传输有功减少,此时SSSC工作在感性模式下,相当于在线路中串入1个电感,增大了线路电抗,其注入电压相角为负值。这说明SSSC能在相同的容性和感性范围内调节线路功率,相比其他FACTS元件只能在容性或感性范围内调节线路功率,SSSC拥有更大的调节范围。
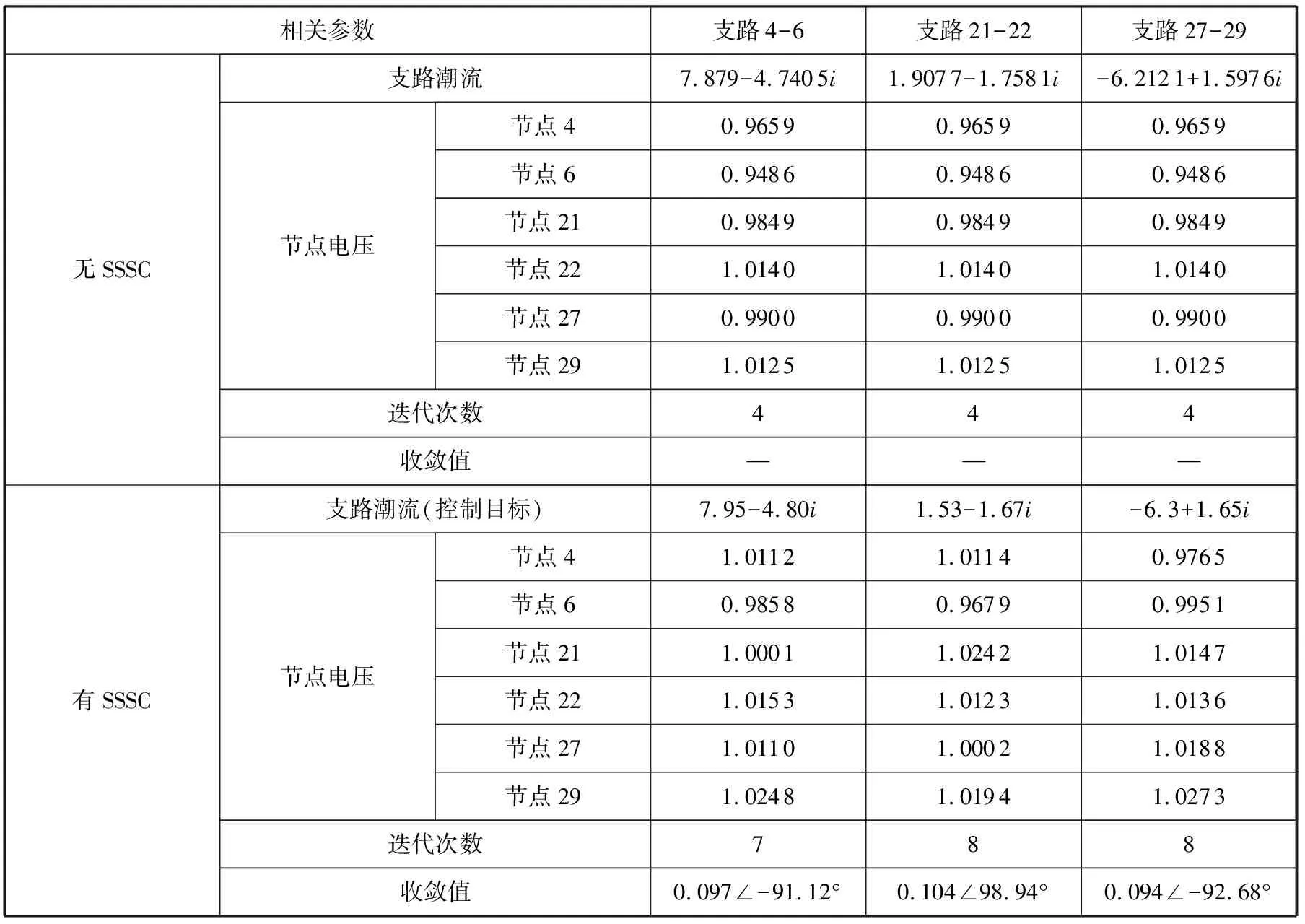
表1 IEEE-30节点系统不同支路装SSSC的潮流计算
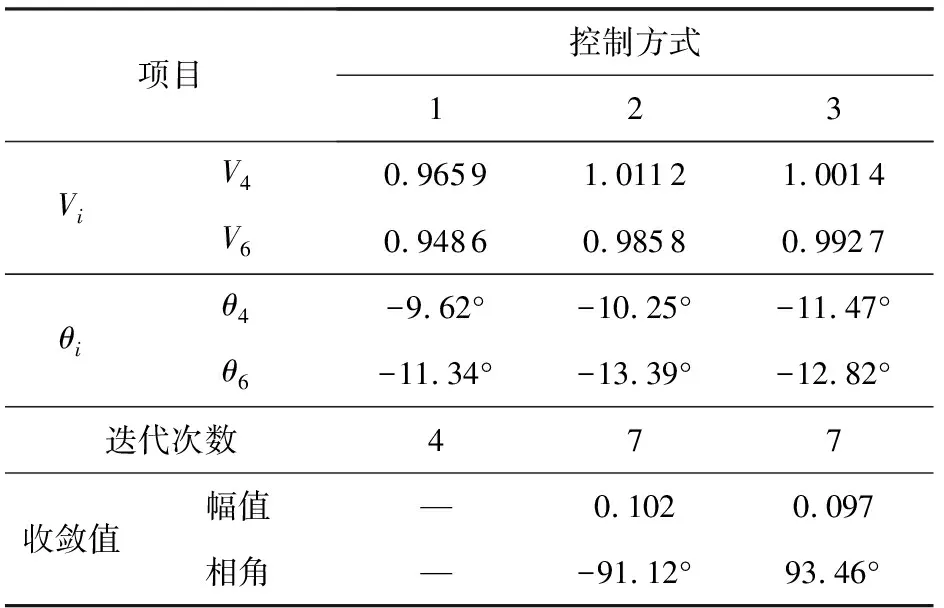
表2 IEEE-30节点系统不同控制目标时SSSC的潮流计算
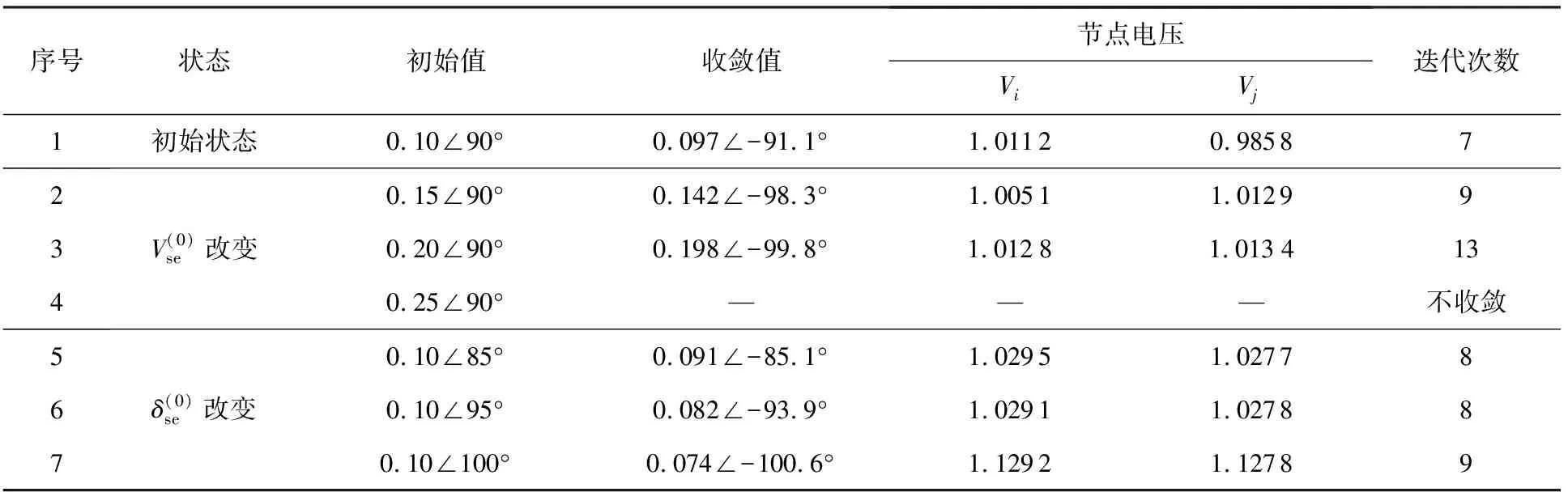
表3 不同Vse,δse初始值时SSSC的收敛情况
表3给出了不同的Vse,δse初始值对潮流计算收敛性的影响。在IEEE-30节点系统中选取线路4-6,SSSC安装在节点4的出口处,所有计算中SSSC的控制目标是相同的,其支路潮流控制目标为7.87-3.49i。
4 结论
本文基于带SSSC联络线基本结构模型,提出了一种在联络线功率控制目标给定的条件下含SSSC网络的潮流算法。该方法不必修改原有网络的节点导纳矩阵,只将SSSC对网络的影响转化为节点等效注入功率,推导了节点注入功率与SSSC结构参数的关系表达式,并根据给定功率控制目标建立新的状态方程,选取新的状态变量,将SSSC对网络的影响转移到对潮流方程的修正中去。同时根据IEEE-30模型参数,验证了本文算法的有效性。
参考文献:
[1]陈葛松,叶海蓉.可控串联补偿技术及其应用介绍[J].国际电力,2004,8(4):43-48.
[2]赵学强.阳城-淮阴500 kV线路固定和可控串补方案的比较研究[J].中国电力,2002,35(1):52-56.
[3]L Zhang, M L Crow,Z Yang. The steady state characteristics of an UPFC integrated with energy storage[J].Power Engineering Society Winter Meeting,2001,3(28):1232-1237.
[4]赵洋,肖湘宁.利用SSSC阻尼电力系统低频振荡[J].电力系统自动化,2007,31(17):40-44.
[5]ZHANG Xiaoping. Advanced modeling of the multicontrol functional static synchronous series compensator (SSSC) in newton power flow[J].IEEE Traps on Power Systems, 2003,13(4):845-851.
[6]ZHANG Xiaoping. Modelling of the interline power flow controller and the generalized power flow controller in newton power flow[J].Generation,Transmission and Disrtibution,2003,150(3):317-323.
[7]刘明波,谢敏,赵维兴.大电网最优潮流计算[M].北京:科学出版社,2010.
[8]王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2006.
[9]陈珩.电力系统稳态分析[M].3版.北京:中国电力出版社,2007.
[10]李光琦.电力系统暂态分析[M].3版.北京:中国电力出版社,2007.
[11]孙智峰.发电厂自动电压控制系统应用[J].华电技术,2011,33(5):35-36.
[12]李渊.现代电力系统病态潮流算法的研究[J].华电技术,2009,31(5):24-27.
