高速铁路接触网避雷线高度设计方法研究

2020-07-13曹晓斌田明明李瑞芳

铁道学报 2020年6期

曹晓斌，田明明，李瑞芳，高保

(1.西南交通大学电气工程学院,四川成都 610031；2.广东电网公司惠州供电局，广东惠州 516001；3.中铁二院工程集团有限责任公司，四川成都 610031)

接触网是高速列车取电的唯一途径，接触网遭受雷击后将导致列车供电中断，严重情况下危害列车运行安全。我国高速铁路牵引供电系统接触网大部分全线未设置避雷线，仅仅在关键部位设置避雷器来防止过电压[1-2]。文献[3-5]对我国高速铁路雷电防护体系进行分析和研究，并且提出参考电力系统设计架设专用避雷线，或升高 PW线回流线兼做避雷线的防雷方案，可以有效提高接触网雷电防护性能。文献[6-7]也对高速铁路接触网雷击跳闸率的计算方法进行了分析和研究。

随着我国高速铁路的发展，接触网防雷也逐渐引起了注意，一些地区为了降低雷击跳闸率，在接触网上增设了专用避雷线。避雷线高度关系到接触网雷电防护性能，因此在接触网防雷设计中避雷线架设高度也是一个关键参数，有必要展开进一步研究。高速铁路接触网结构相比输电线路而言其导线结构及排列方式更为复杂，特别是对于复杂站场，因此在计算避雷线的屏蔽范围时工作量较大。滚球法作为国际电工委员会(IEC)推荐接闪器保护范围计算方法，具有计算过程简单、计算工作量小、计算结果可靠等优点。

本文结合高速铁路接触网自身结构的特点，并结合现有的一些避雷线屏蔽计算方法，提出一种适合工程推广应用的避雷线高度设计方法。以单、复线铁路接触网为例，推导了避雷线高度的计算公式，并对接触网耦合系数和雷击跳闸率进行分析；对滚球半径的影响进行分析，推荐选用适合不同地区的滚球半径，为避雷线架设提供设计依据。

1 避雷线屏蔽性能计算方法

1.1 电气几何模型

20世纪60年代，文献[8-14]建立了雷电屏蔽性能分析的电气几何模型(Electro-geometric Model, EGM)，广泛应用于防雷计算中。以接触网EGM模型为例，图1为复线铁路情况下接触网EGM模型，图中R表示击距，下标g、F、T、b分别对应大地、馈线、接触线、避雷线的击距。通过调整避雷线高度可以保证接触网各导线被有效屏蔽，利用EGM模型可以有效分析图中避雷线的屏蔽情况。

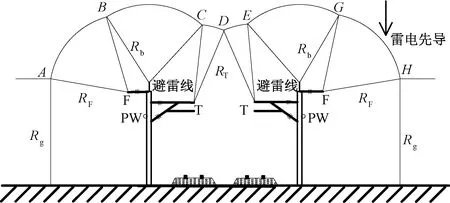
图1 复线情况下接触网EGM模型

1.2 滚球法

滚球法基于EGM模型并在其基础上变化而来，它是IEC推荐的计算接闪器保护范围的一种方法，我国相关规程中也把它作为一种标准设计方法[15-18]。滚球法的应用如图2所示，图中灰色部分为被避雷线屏蔽部分。利用滚球法可以计算得到接闪器的防雷效果，计算过程简单，应用便捷。

图2 滚球法应用

根据滚球法的计算方法，如图2所示，球体半径为R，避雷线架设高度为hx，则其保护半径bx为

( 1 )

1.3 滚球法与电气几何模型对比

滚球法在EGM模型基础上演化而来，像铁路这种周边情况复杂，如铁路两边分布有桥梁、山坡以及多条铁路并行复线铁路等复杂情况，可以有效推广。EGM应用过程中，首先要确定击距、暴露宽度等参数，应用过程复杂。滚球法的应用过程是以某一确定半径的球体，沿着布置有避雷线的铁路接触网两端滚动，球体无法触及的地方就是避雷线的保护范围，其应用过程如图3所示。

图3 复杂情况下滚球法应用

2 滚球法计算避雷线设计高度

2.1 计算参数

通过上面介绍可知，滚球法不仅可以分析避雷线防雷效果，也可以用来计算避雷线最佳防护高度。高速铁路主要以AT供电方式为主，因此以AT供电方式下单线和复线铁路为例，通过滚球法分析避雷线的架设高度。图4为高速铁路接触网单线情况下几何参数示意图，图中接触网导线包括T线、F线、PW线。复线铁路计算中轨道中心间距按照常规设定为6 m。雷击接触网主要通过直击F线以及T线对接触网造成危害，因此需要选择一个合适的高度架设避雷线，来分析避雷线的屏蔽效果。

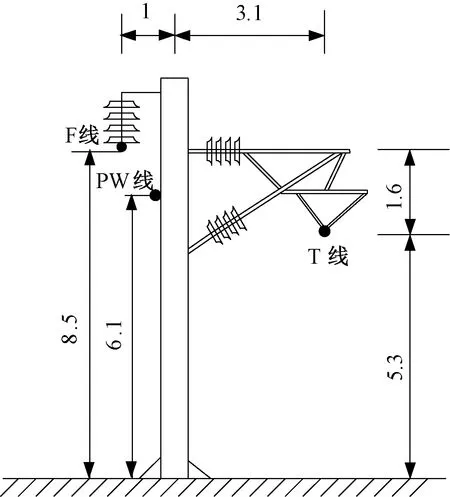
图4 接触网结构参数(单位：m)

2.2 避雷线高度的计算

(1)单线铁路避雷线高度计算

在单线接触网情况下，当球体(图5中的O1、O2)只触及到大地和被保护的导线(接触线、馈线)时，经过支柱中心线方向与球体的交点(图5中的C、D)得到避雷线最低架设高度。当需要同时保护接触线T、馈线F时，计算中取两个高度中较大值作为避雷线的最后架设高度，这样馈线F和接触线T均在避雷线的保护范围内。

图5 单线铁路接触网避雷线高度计算

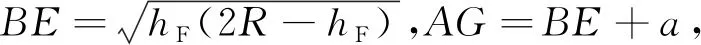
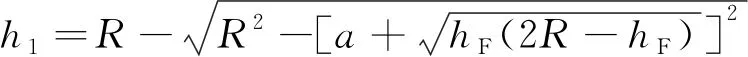
( 2 )

同理当以保护馈线设计避雷线高度时可以得到

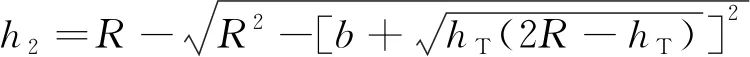
( 3 )

式中：R为滚球球体半径；hF为馈线F线到地面的垂直高度；hT为接触线T线到地面的垂直高度；b为接触线水平支架的长度；a为馈线水平支架的长度。避雷线设计高度以h1、h2中较大值作为设计依据。

(2)复线铁路避雷线高度计算

复线情况滚球法的计算过程如图6所示。利用滚球(图6中O1、O2、O3)沿着被保护的导线滚动，确定避雷线的安装高度(图6中C1、C2)和保护范围。通过分析发现，如果按照第一类滚球半径30 m计算，此时接触线已在保护范围内，因此复线接触网只需考虑对馈线F线的保护。

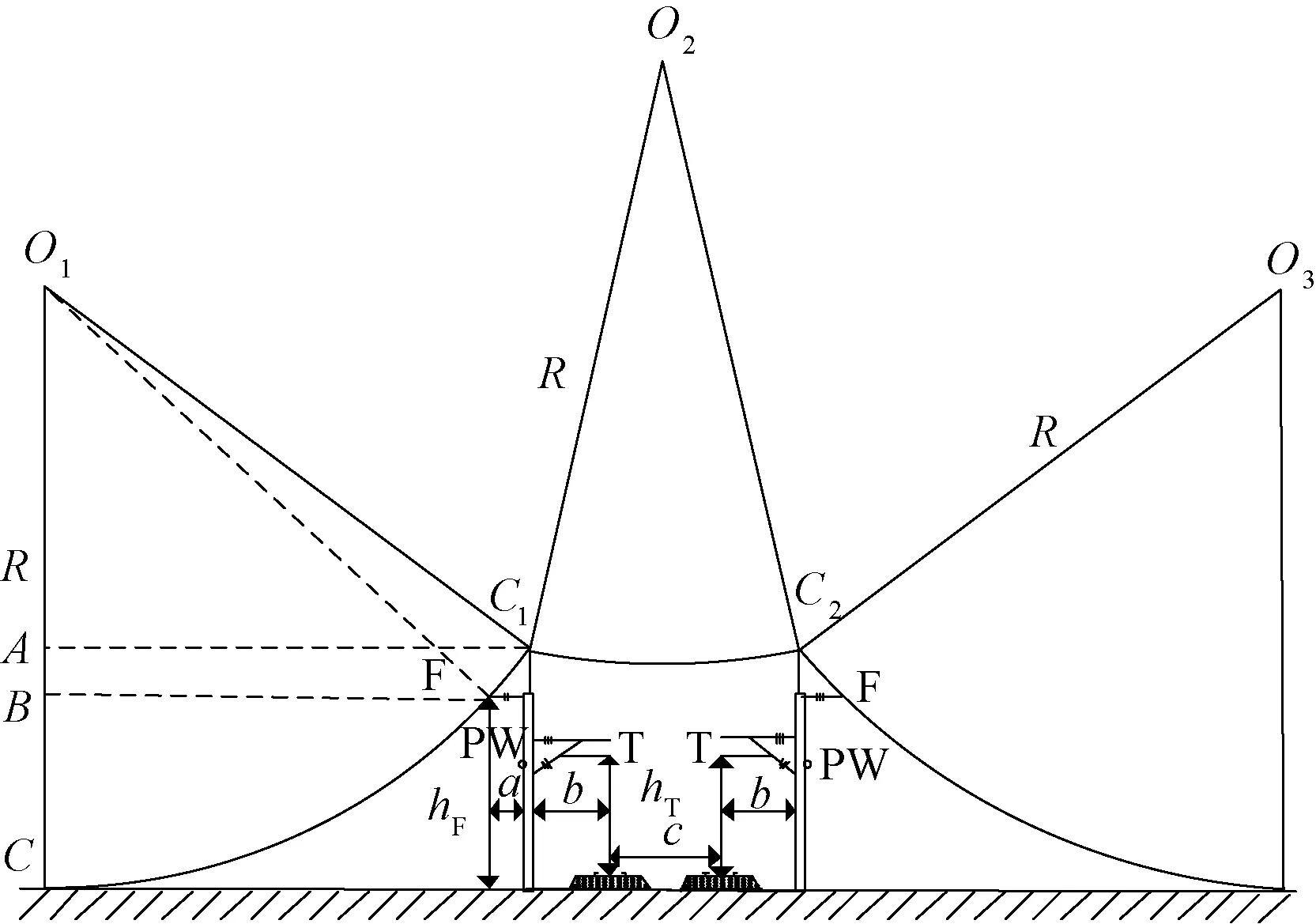
图6 复线铁路接触网避雷线高度计算

同理，通过计算可以得到复线情况下避雷线的设计高度为

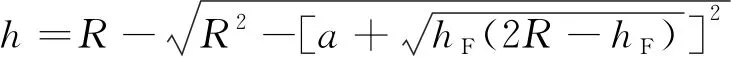
( 4 )

2.3 避雷线高度与滚球半径关系

通过前面分析得到了避雷线设计高度的计算方法，将滚球半径和接触网结构参数带入到计算公式中可以得到避雷线设计高度，避雷线高度与滚球半径关系如图7所示。

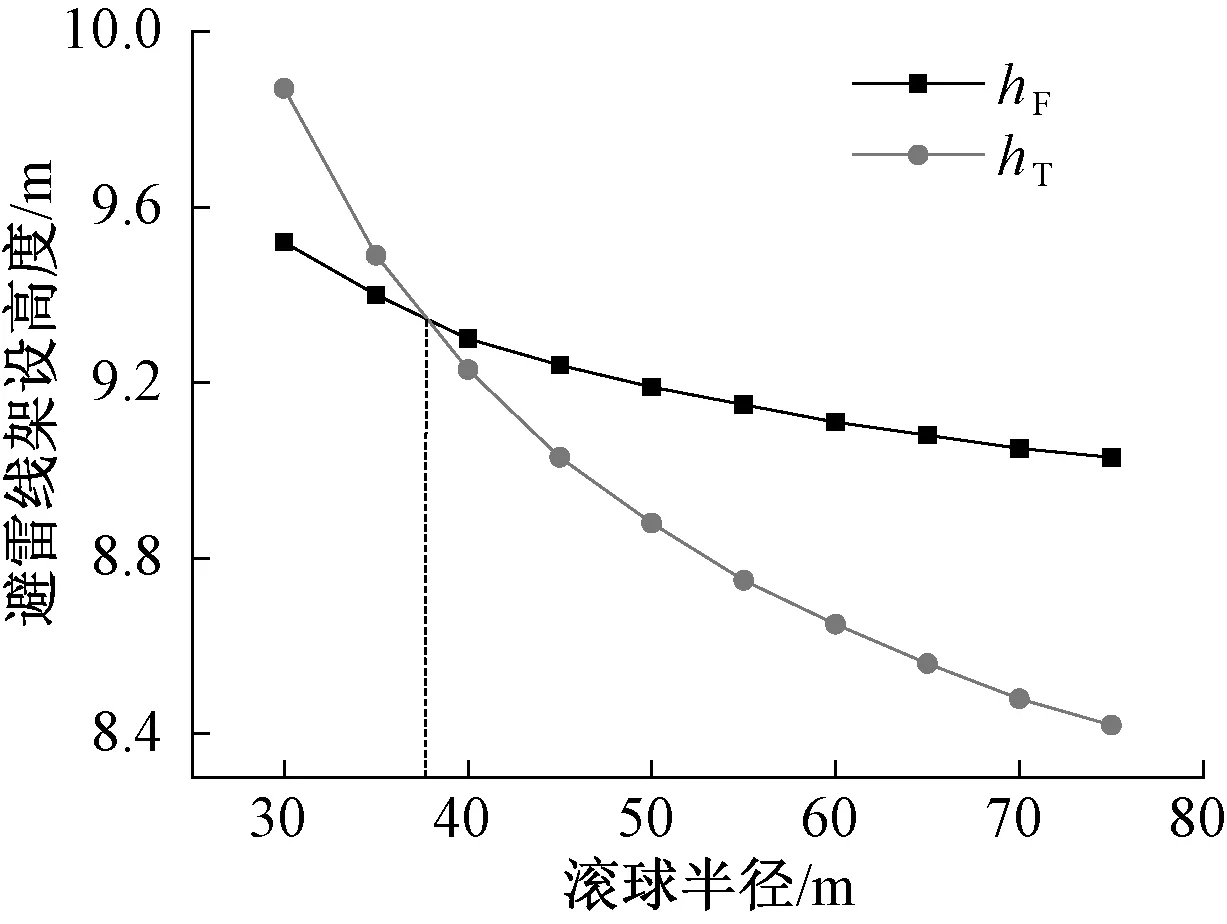
图7 避雷线高度与滚球半径的关系

单线铁路需要考虑避雷线对馈线和接触线的保护，避雷线高度选取二者中较大者作为最终的安装高度(图7中hF、hT)，而复线情况则仅需考虑对馈线的保护(图7中hF)。从图7可以看出，滚球半径与避雷线的高度成反比。进一步计算可以知道，当R<37 m时，避雷线主要考虑对接触线进行保护，当R>37 m时，避雷线主要考虑对馈线进行保护，R=37 m时，两种方式计算结果相同。下面将进一步分析避雷线高度与防雷性能关系，从而最终选取推荐合适的滚球半径。

3 避雷线高度对接触网雷电防护性能影响

3.1 避雷线高度对接触网耦合性能的影响

在防雷计算过程中，耦合系数是一个重要参数，本节将讨论避雷线高度对耦合系数影响及其计算方法。雷击避雷线后雷电流分布如图8所示，采用麦克斯韦方程组求解耦合系数。由于接触网导线的排列方式不同于电力系统输电线路各导线的排列方式，因此其导线耦合系数的计算不能直接采用电力系统耦合系数计算公式。公式中a，b，c，d分别对应避雷线、馈线、接触线、PW线。

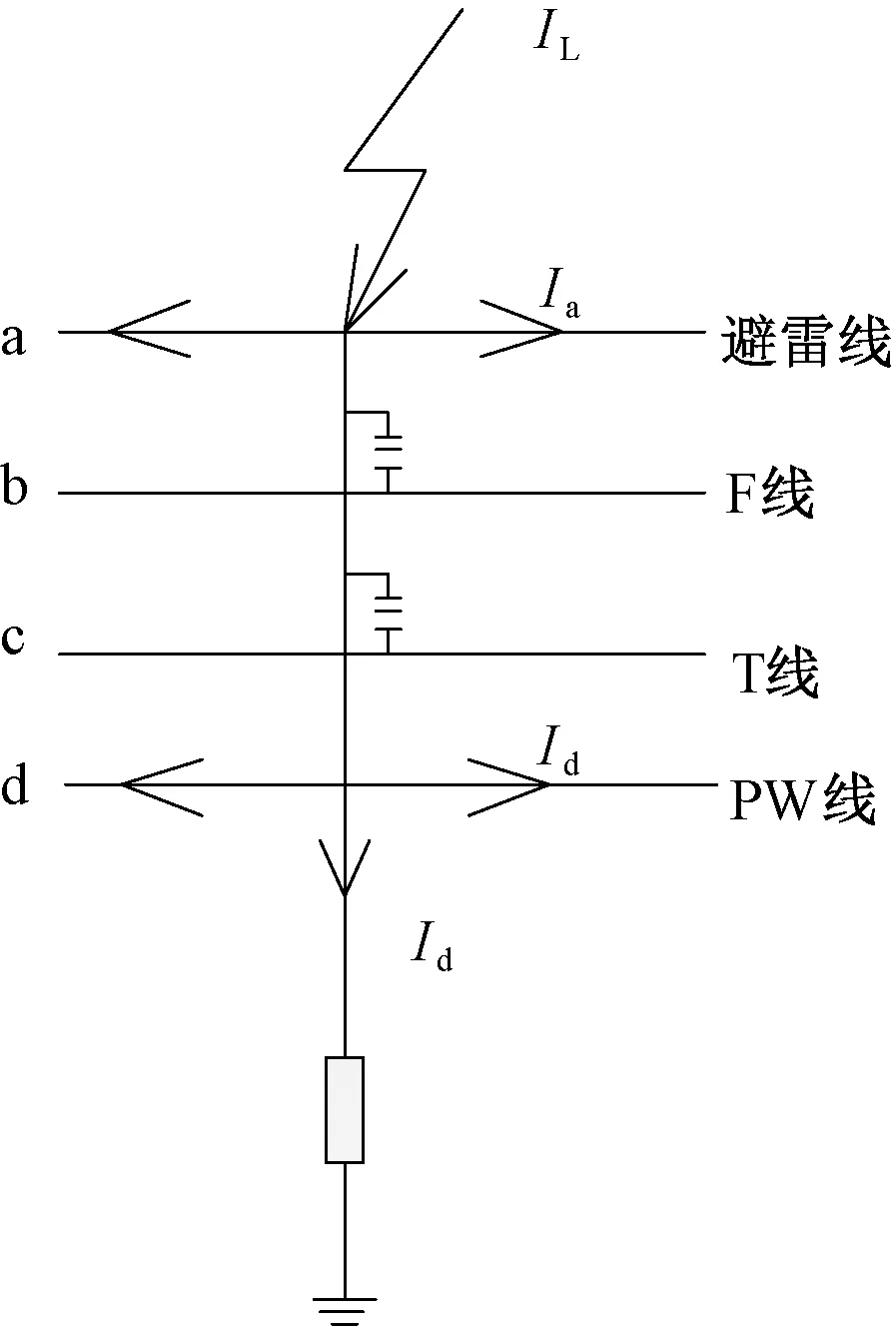
图8 雷击避雷线电流分布

( 5 )

Uk、Ik(k=a，b，c，d)分别表示对应导线的电压及电流；Zkk、Zkn(k、n=a，b，c，d)分别表示对应导线的自波阻抗和互波阻抗，其计算公式参考文献[19]。

由图8可知，馈线和接触线通过绝缘子与地绝缘，因此Ib=Ic=0。本文计算中不考虑支柱压降，认为Ua=Ud。计算得到馈线、接触线耦合系数kb、kc为

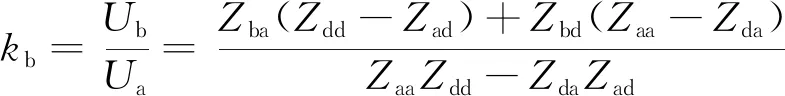
( 6 )

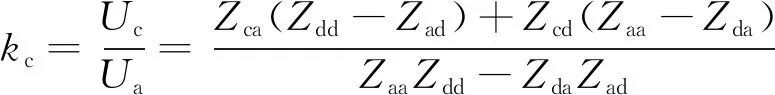
( 7 )

分别带入参数计算T线以及F线的耦合系数，随着避雷线架设高度的变化其耦合系数的结果如图9所示。

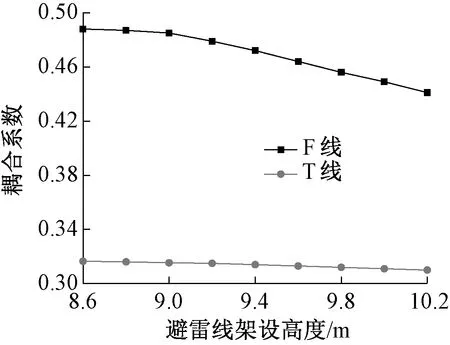
图9 避雷线高度与耦合系数关系

根据计算结果可以看出，馈线F耦合系数大于接触线T的耦合系数。从图8可以看出，馈线F距离上更接近避雷线，因此它们之间的耦合性能更好，与计算结果吻合。根据所给的参数得到馈线的耦合系数为0.45左右，接触线的耦合系数为0.31左右，并且馈线和接触线耦合系数均随着避雷线高度的增加而逐渐减小，馈线耦合系数计算结果受避雷线高度的影响更明显。

3.2 避雷线架设高度对雷击跳闸率的影响

当避雷线架设高度发生变化时，接触网屏蔽性能各方面会受到影响，其雷击跳闸率也会发生变化，本节计算雷击跳闸率的变化。计算方法参考文献[4,6]中跳闸率计算方法。计算结果见表1、表2。

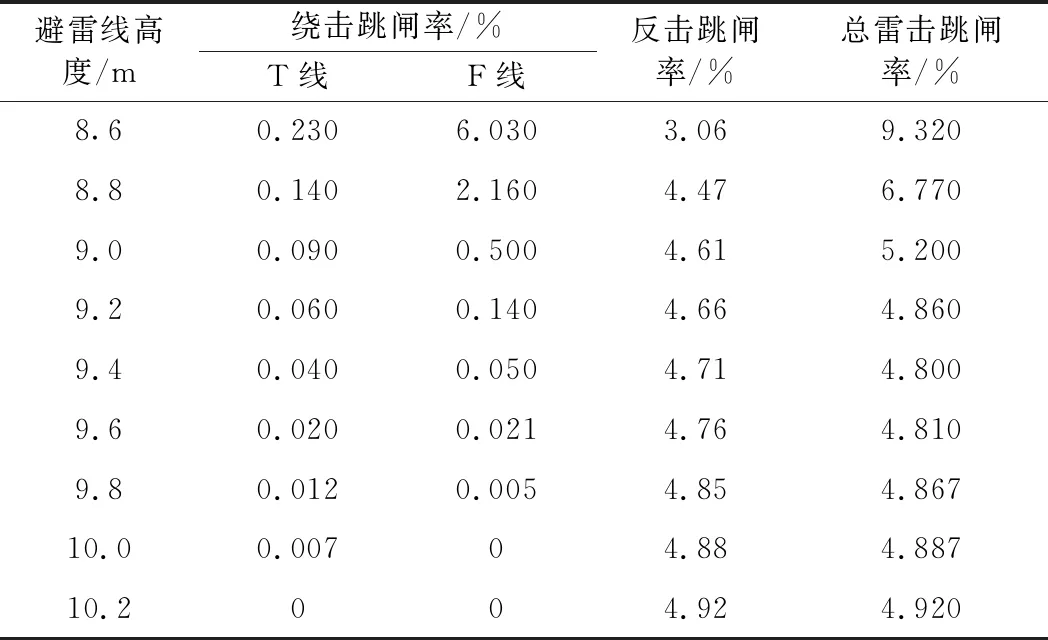
表1 单线铁路雷击跳闸率

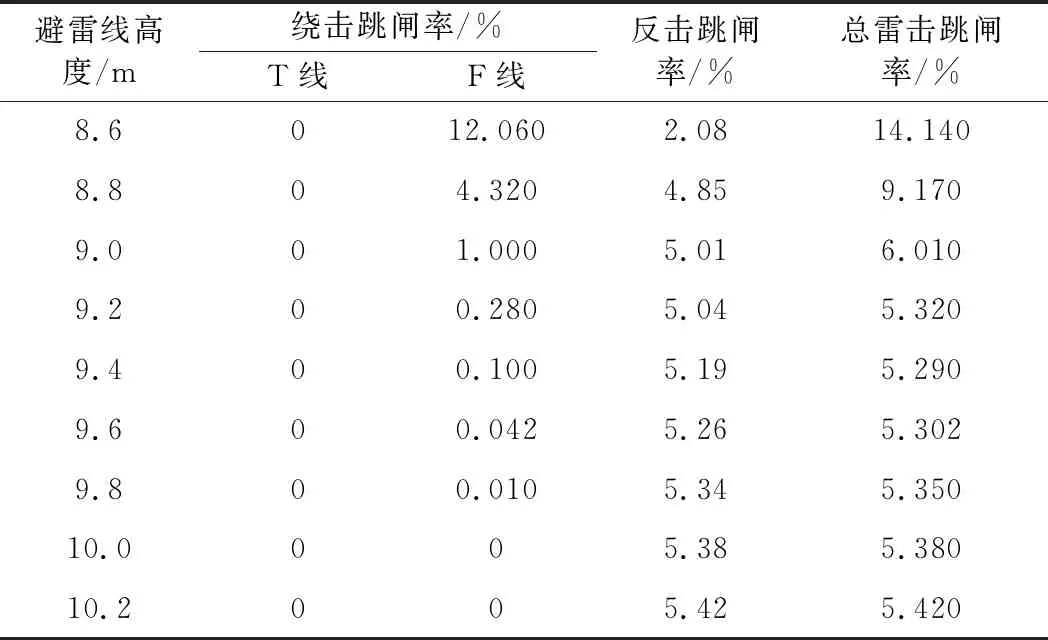
表2 复线铁路雷击跳闸率

表1、表2计算了单、复线铁路雷击跳闸率随避雷线高度变化情况，计算过程未考虑感应雷击跳闸率的影响。从计算结果可以看出，复线铁路接触线T线雷击跳闸率为0，主要是因为复线铁路接触线T线所对应的绕击区间被屏蔽，因此复线铁路架设避雷线设计过程中无需考虑接触线影响，此计算结果与滚球法分析相同。复线铁路馈线绕击跳闸率是单线铁路馈线绕击跳闸率的2倍。随着避雷线高度增加，复线铁路反击跳闸率以及总跳闸率均大于单线铁路。

从表1、表2可以看出，无论是在单线还是复线区段，随着避雷线高度增加，绕击跳闸率逐渐降低，反击跳闸率逐渐增加。通过进一步分析可知，随着避雷线高度增加，避雷线引雷范围越大，其反击雷击跳闸率逐渐增加，从而导致总雷击跳闸率逐渐增加，因此在选择避雷线高度时要考虑反击雷击跳闸率的影响。避雷线高度选择要同时兼顾考虑反击和绕击跳闸率，要选择一个最优的高度，使总雷击跳闸率最低。

3.3 滚球半径的选择

根据我国防雷相关规范将滚球半径划分为三类，R1=30 m，R2=45 m，R3=60 m。参考这三类滚球半径应用2.2节推导计算公式分别计算单、复线铁路接触网对应的避雷线设计高度，其结果见表3。

表3 避雷线高度计算结果 m

根据设计高度并参考3.2节雷击跳闸率计算结果可以发现，采用不同滚球半径计算得到的结果相差较小，因此为了便于推广，在避雷线高度设计过程中可以采用规程中推荐滚球半径计算。一般情况下认为雷暴活动越频繁的地区，滚球半径选取越严格，但是通过本文计算发现，采用第一类滚球半径设计避雷线高度雷击跳闸率反而偏高，这主要是由于反击雷击跳闸率升高的原因。因此，在雷暴活动不频繁的地区，可以考虑适当降低避雷线设计高度，采用第三类滚球半径，可以节约成本；在雷电活动严重的地区，提升避雷线设计高度，建议采用第二类滚球半径确定避雷线设计高度。