基于模块化多电平换流器的静止无功补偿装置的研究
2014-09-10郑滨豪
郑滨豪
(杭州华电半山发电有限公司,杭州 310008)
0 引言
在电力系统中,各种无功负荷不仅增加了线路的损耗,还降低了电能质量。实时动态快速地补偿无功功率,对于提高电网稳定性、保证电压水平具有重要意义。
传统的无功补偿装置(动态无功补偿装置TSC,静止式无功补偿装置SVC等)动态响应速度慢、调节特性差、补偿电流谐波含量高。随着电力电子技术的发展,基于电力电子变换技术的换流器不断更新。电力电子变换器按照换流方式的不同可以分为电压源型换流器(VSC)和电流源型换流器(CSC)。CSC的换流方式必须有源,并且只能在过零点换相,相比之下VSC就能弥补这些不足。近年来由德国学者提出的新拓扑——模块组合多电平变流器(MMC)更是基于基本的VSC单元设计出的级联型多电平换流器[1]。MMC通过子模块的组合级联,叠加子模块的电压后能很好地逼近正弦波,降低谐波含量;模块组合的设计思路也能很好地实现冗余控制,扩展到不同的电压等级,同时可以省去体积庞大的变压器和滤波装置。
鉴于MMC具有以上优点,采用MMC作为电力系统中高压等级的静止无功补偿装置,研究装置的基本原理和数学模型,设计了dq前馈解耦的控制系统,采用最近电平逼近策略实现级联子模块的电容电压均衡,最后通过仿真验证了基于模块化组合多电平换流器的静止无功补偿装置的良好性能。
1 MMC的工作原理
三相MMC的拓扑结构如图1所示,MMC中每相包含2个桥臂,3相共6个桥臂,每个桥臂由n级联个子模块(SM)和桥臂电抗器(L0)组成,R0是桥臂等效阻抗。如图1所示,每个SM由2个带反并联二极管的绝缘栅双极型晶体管(IGBT)、1个直流电容器和1个机械旁路开关组成。设子模块的参考电压为Vc,则通过控制2个IGBT的不同组合,可以实现每个子模块对外的输出控制,具体开关状态见表1。

图1 MMC主电路拓扑

表1 子模块的开关状态
n个SM级联起来,每个桥臂能产生0~nVc的电压,可简化为输出幅值为0~nVc的理想电压源。设换流器出口侧交流电压、电流波形为纯正弦波,则
uj=Usinωt,
(1)
ij=Isin(ωt+φ) ,
(2)
式中:φ=±90°。
MMC交流侧电压、直流电压与桥臂电压间关系为
(3)
(4)
由式(3)、式(4)可得
(5)
Udc=Vpj+Vnj,
(6)
式中:j=a,b,c,下同。
由于3个相单元的对称性,直流电流Idc在3个相单元之间均分,即流过每个相单元的直流电流为Idc/3,又由于上下桥臂的对称性(上下桥臂的换流电抗相等),交流相电流在上、下桥臂间均分,即流过每个桥臂的交流电流为相电流的一半。计入换流器运行时相单元中的交流环流icirj(2倍工频)[2],则每一相上下桥臂的电流分别为
(7)
(8)
2 MMC的调制与均压策略
目前,MMC的调制方法主要有脉冲宽度(PWM)调制法和阶梯波调制法2种,应用在中高压的无功补偿领域,MMC级联的子模块数很多,采用PWM调制需要给每个子模块加载1个载波和调制波,控制系统非常复杂,甚至难以实现,通时PWM的开关频率会很高,损耗很大,装置的效率很低。因此,阶梯波调制法是比较合适的选择。在电平数足够多的情况下,阶梯波调制产生的波形谐波含量也很小。目前常用的是2种阶梯波调制法:特定谐波消去法(SHE)和最近电平逼近法(NVL)[3]。由于SHE方法需要求解非线性方程组,并进行离线φ计算和查表,且当电平数大于5时算法将变得相当复杂,因此不适合用于电平数较多的MMC拓扑。
基于NVL调制法的换流器交流侧输出电平等于和参考正弦电压最接近的电平,即将参考波除以每个子模块的额定电压,然后四舍五入取整,得到需要的子模块个数为
(9)
(10)
式中:Npj和Nnj分别为上下桥臂需要投入的子模块的个数;函数NINT(x)是对x进行取整的函数。
通过式(9)、式(10)得到上下桥臂需要投入的子模块数,为了确保各个SM中电容电压都维持平衡状态,采用如下均压策略选择具体投入哪些子模块:按照子模块的电容电压值从小到大排序,然后采样桥臂电流值,当桥臂电流为正时(充电),先触发电压最低的Npj和Nnj个子模块;当桥臂电流为负时(放电),先触发电压最高的Npj和Nnj个子模块。最近电平逼近法流程如图2所示。
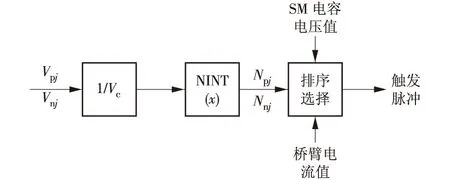
图2 最近电平逼近法
3 dq解耦控制
换流器交流侧三相电压、电流经park变换矩阵

(11)
变换后,在dq坐标系下的交流侧动态微分方程为
(12)
式中:id和iq分别为输入换流器的有功、无功电流;usd和usq分别为系统电压的d轴、q轴分量;ucd和ucq分别为换流器侧电压的d轴、q轴分量;L为交流侧电抗器的电感;R为该电抗器电阻[4-5]。
前述的均压策略只是保证了桥臂中的子模块之间的电压相等,为保证整个直流侧电压恒定,需要加入直流电压控制,因此,无功功率和直流侧电压解耦控制框图如图3所示。
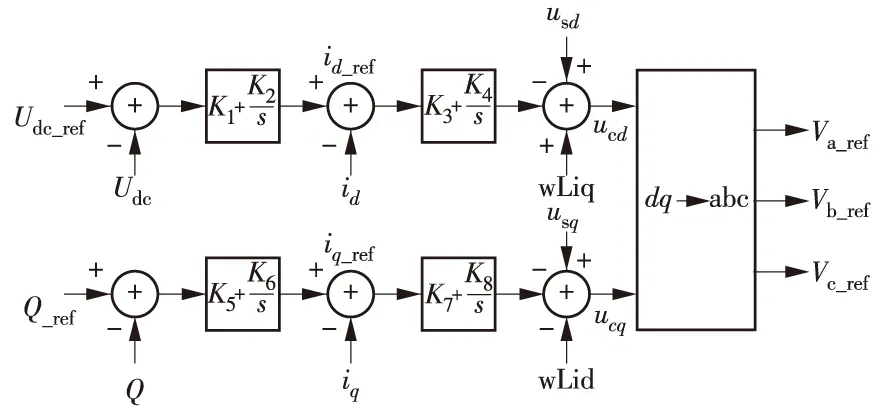
图3 有功、无功解耦控制
4 仿真验证
为了验证基于MMC的静止无功补偿装置的可行性和控制策略的有效性,在 PSCAD/EMTDC 软件平台搭建详细的仿真模型。仿真系统中MMC每桥臂有70个SM,共420个;直流电容C为8 000 μF,其额定电压Vc为1 ;缓冲电感Ls为15 mH;交流相电抗器L为5 mH;MMC交流侧接无穷大交流系统,电压等级为35 kV;换流器交流输出电平数最多为71。具体参数见表2,仿真电路结构如图4所示。

表2 仿真系统主要电路参数

图4 仿真电气原理
仿真系统中,直流电压控制位为60 kV,在0~0.02 s内,无功功率设定值输出为0;在0.02~0.25 s内,无功功率设定值为-20 MV·A(以系统流向MMC的方向为正);在0.25~0.50 s内,无功功率设定值为-40 MV·A;在0.50~0.75 s内,无功功率设定值反转为40 MV·A;在0.75~1.00 s内,无功功率设定值为20 MV·A。
图5显示了MMC单相上下桥臂输出的电压,图6显示了MMC对交流侧输出的三相电压,这2张图均显示了71电平逼近的阶梯波已经非常接近正弦波,谐波含量非常低;图7显示了交流电流正弦性,谐波含量很低;图8为直流电压,从图中看出直流电压控制非常稳定;图9显示了无功功率跟随给定值效果良好;图10显示了上下桥臂的电流值;图11显示子模块电容电压平衡效果良好,电容电压在额定电压附近波动。综上所述,仿真验证了MMC的拓扑、电容电压平衡控制策略和功率解耦控制策略的有效性。

图5 单相上下桥臂电压

图6 MMC输出电压

图7 交流三相电流

图8 直流电压

图9 无功功率参考值和实际值

图10 桥臂电流

图11 子模块电容电压
5 结论
本文在介绍MMC工作原理的基础上,通过理论推导得出了桥臂电压和电流的表达式,提出了dq解耦的功率控制方法和子模块电容电压平衡策略,推导了MMC交流侧的微分模型,并验证了基于MMC的无功补偿装置的可行性,对上述的控制策略进行了71电平含420个SM的三相MMC模型的计算机仿真,仿真结果验证了理论推导和控制方案的可行性。
参考文献:
[1]Marquardt R,Lesnicar A.New concept for high voltage-modular multilevel converter[C]//Power Electronics Specialists Conference (PESC).Aachen:IEEE,2004:1-5.
[2]管敏渊,徐政,屠卿瑞,等.模块化多电平换流器型直流输电的调制策略[J].电力系统自动化,2010,35(2):48-52.
[3]胡鹏飞,江道灼,郭捷,等.基于晶闸管换向的混合型多电平换流器[J].电力系统自动化,2012,36(21):102-107.
[4]郭捷,江道灼,周月宾,等.交直流侧电流分别可控的模块化多电平换流器控制方法[J].电力系统自动化,2011,35(7):44-47.
[5]管敏渊,徐政.模块化多电平换流器子模块故障特性和冗余保护[J].电力系统自动化. 2011,35(16):94-98.
