Research of WSN Node Localization Technology Based on Six-Element Array for Ultrasonic Ranging*
2014-09-08ZHAOQingqingHUANGLiangFUXianfengLIMingyuanDUANWeijun
ZHAO Qingqing,HUANG Liang,FU Xianfeng,LI Mingyuan,DUAN Weijun
(School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710072,China)
Research of WSN Node Localization Technology Based on Six-Element Array for Ultrasonic Ranging*
ZHAO Qingqing,HUANG Liang,FU Xianfeng,LI Mingyuan,DUAN Weijun*
(School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710072,China)
For the high accuracy,wide range and stable performance,the ultrasonic positioning technology is becoming an important research point in wireless sensor networks.This paper presents and implements a six-element array ultrasonic sensor and a TDOA ranging experiment。It analysis the ranging error and realizes node localization using geodesic distance based multidimensional scaling positioning algorithm.The MATLAB simulate results show that the geodesic distance MDS algorithm can achieve higher accuracy than Trilateration and Multilateration.
wireless sensor networks;six-element array of ultrasonic ranging;multi-dimensional scaling;time difference of arrival;node self-localization
近些年来,随着物联网技术的迅猛发展和应用,无线传感器网络WSN(Wireless Sensor Networks)已经成为当今生活中不可或缺的一部分。无线传感器网络的众多应用场合如战场监控、环境监测、室内定位与跟踪、智能仓储和物流管理等,不知道来源位置的传感器感知数据往往是没有意义的,因而无线传感器网络节点的自身定位技术就显得非常重要[1]。
传感器网络定位技术是一项复杂的技术,涉及的节点数量众多,覆盖范围广泛。根据网络中是否存在锚节点可以将算法分为节点自定位算法和基于锚节点辅助的定位算法,无锚节点的节点自定位算法的研究刚刚兴起,而且在实际应用中对硬件要求较高,操作复杂度也较大,因此本文只对基于锚节点的定位技术进行研究。
在特定的网络环境下,基于锚节点的WSN定位算法在定位精度、定位时间及定位可靠性等方面仍存在巨大的挑战[2]:①网络环境多样性。在某些应用中,传感器节点随机分布于无人值守的区域中,网络环境复杂多样,因而算法能在各种环境中保证定位精度则尤为重要。②节点移动性。动态网络节点定位不但面临成本、能耗、环境多样性的挑战,还应更多的考虑位置信息的时效性以及由于网络形状改变而带来的拓扑结构变化。③可靠性。由于网络的开放性,节点常常受到攻击,例如在常受到攻击的军用领域,事件发生的位置信息的可靠性是决定战争胜利的关键因素之一,因此可靠性尤为重要。
目前的定位方法主要分为基于距离的(Range-Based)和非基于距离的(Range-Free)两种定位方法。基于距离的定位方法主要有:基于接收信号强度衰减RSSI(Received Signal Strength Indication)定位[3]、基于到达时间TOA(Time of Arrival)定位[4]、基于到达时间差TDOA(Time Difference of Arrival)定位[5]和TOF(Time of Flight)定位[6]等;非基于距离的定位方法则主要有质心算法、MDS-MAP[7]算法、距离向量-跳段DV-HOP(Distance Vector-HOP)算法[8]等。马震等提出一种基于MDS-MAP分布式传感器网络定位算法MDS-MAP(D)[9]。该算法将传感器网络划分为簇,由簇头节点执行次序多维定标算法得到局部网络中各节点的绝对坐标。相比于MDS-MAP算法,MDS-MAP(D)可有效降低节点定位的计算复杂度,但在定位精度上的优势并不明显。
基于TDOA的定位算法通常利用超声波与RF信号的传播速度差异计算信号到达时间差进行测距,然后采用三边定位算法进行位置估计。基于超声波的TDOA技术测距精度高,系统具有较高的定位精度,因此获得广泛应用。
目前典型的基于超声波测距的定位系统主要有Cricket[10]、AHLos[11]和SpiderBat[12]等。Cricket定位系统采用基于最小二乘法和卡尔曼滤波的三边定位算法逐个节点迭代定位;AHLoS系统采用原子式、协作式和迭代式的最大似然估计方法定位。这两类系统均采用基于超声波和RF到达时间差的TDOA方法测距,系统定位精度在20~30cm,但由于测距范围较短(通常在10m以内),限制了该类系统的应用范围。SpiderBat则采用超声波传播时间测距,超声波测距节点由四组独立可控的超声波收发传感器和一个数字罗盘组成,采用四组超声波收发传感器解决了超声波波束角有限的问题,增加了测距范围并提高了测距精度,每个节点配备了一个数字罗盘,这样收发双方两个节点就能分别获得它们之间的绝对角度。SpiderBat的定位过程与Cricket系统相类似。
本文在自主研发的超声波六元阵测距平台上,研究并提出一种基于超声波TDOA测距的WSN节点定位技术,采用基于测地距离的多维定标(Geodesic Distance Based Multi Dimensional Scaling)[13]定位算法,可有效实现网络高精度相对定位和绝对定位,从而为WSN提供更好地节点自身定位服务支持。
1 超声波测距
本文采用基于超声波的TDOA测距技术,利用超声波信号和射频信号获取TDOA所需的时间差,同时改进超声波收发电路,设计实现了超声波六元测距阵列,为无线传感器网络定位算法提供高精度测距。
1.1 TDOA测距原理
TDOA测距技术是超声波测距系统中最常用的技术之一,主要有回波测距和非反射式测距两种方法[14]。与回波测距法相比,非反射式测距过程中的超声波发送信号不经反射直接到达接收端,避免了多径反射以及信号反射时的能量损耗和波形失真。因此,无线传感器网络中利用超声波信号进行测距时,更多的是采用非反射式测距方法。本文同样采用非反射式的测距方法实现节点间测距。非反射式测距方法要求收、发节点之间保持时间同步,时间同步的精度将直接影响测距精度。测距过程如图1所示。
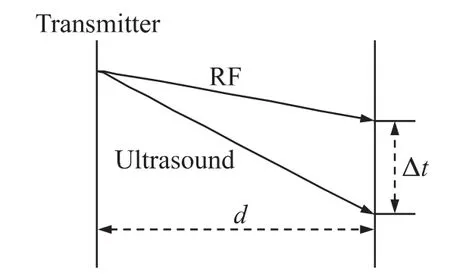
图1 非反射式测距示意图
发送节点同时发送一个RF信号与超声波信号,以RF信号作为时间同步信号标记测距的开始时刻,接收节点只需测出RF信号与超声波信号的到达时间差Δt即可利用式(1)计算出收发节点之间的距离d:

其中vr为RF信号在空气中的传播速度,vu为超声波信号在空气中的传播速度。由于vr≫vu,所以可将式(1)简化为:

1.2 超声波六元阵
由于超声波发射器存在一定的波束角,当超声波接收器不在超声波发射器的波束角范围内或者偏离超声波发射器的角度较大时,接收端很难检测到超声波信号;同样的,单个超声波发射器只能向某个固定方向的一定角度范围发射超声波信号,偏离这个方向的接收节点也很难检测到该发射器发送的超声波信号。为了保证较高的测距精度和定位精度,同时为了提高测距范围,本文设计完成了一种超声波六元阵测距节点,其实物图如图2所示。节点分别利用六组不同方向的超声波收发器实现超声波测距,每组可实现最大15 m距离的测量。这种基于六元阵的设计可以增大信号的覆盖面,有利于超声波信号的接收检测,从而实现二维全向精确测距。

图2 超声波六元阵收发模块实物图
1.3 超声波TDOA测距
TDOA测距模块以超声波六元阵收发模块与JN5148射频模块为硬件平台。超声波接收模块采用阈值检测法对超声波信号进行接收检测。为了弥补环境温度变化对超声波测距精度的影响,本文利用温度传感器采集环境温度对超声波的传播速度进行补偿:
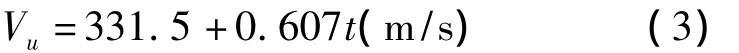
其中Vu为补偿后的速度,t为环境温度(℃);对于软件延时和同步精度差等误差,则利用参量补偿的方式来减小误差。
本文在教学楼走廊对超声波节点进行TDOA测距实验以验证其测距精度。实验中,节点的设计最远测量距离为15 m,测距距离从1 m开始测量并逐渐增加到15 m,每隔1 m进行一组测距实验,共计15组测试数据。为了减小样本测量误差,每组实验测量50次,取多次测量的样本平均值进行比较。测距实验结果如图3所示,样本数据平均误差8 cm,最小误差近似为0,最大误差为26.7 cm,相对测距误差范围为0%到1.335%,平均相对测距误差约为0.4%。
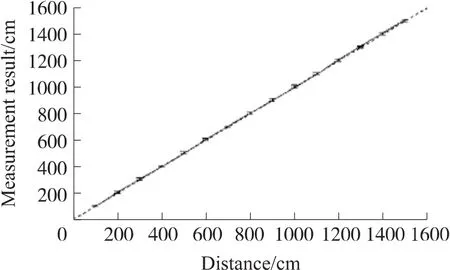
图3 超声波六元阵测距结果
以测距实验取得的平均相对测距误差和最大相对测距误差作为参考,度量系统的定位精度,在算法仿真实验中,所有节点的相对测距误差设为0.4%和1.5%。
2 基于超声波阵列测距的定位算法
为了实现对WSN进行精确定位,本文提出一种基于超声波六元阵进行节点间测距,并采用多维定标进行网络自身定位的WSN定位算法。考虑在一个L×L的二维正方形平面区域中,部署一个包含N个节点的传感器网络,其中有M个锚节点(M≥3),网络中每个节点都包含一个同构的超声波六元阵列传感器节点,可以与其他邻节点互相进行测距,如图4所示。

图4 超声波六元阵定位系统示意图
定位算法采用改进的多维定标算法计算网络坐标,其基本思想是:首先利用节点间的距离信息建立距离矩阵,然后应用MDS算法生成节点相对坐标,当有足够数量的(二维空间3个、三维空间4个)锚节点时,最后通过线性变换将网络相对坐标转化成绝对坐标。定位算法的定位过程主要分成3个阶段:
2.1 构建测地距离矩阵
网络部署完成之后,从全局角度生成网络拓扑连通图,并为图中每条边赋予一个距离值dij。对于在通信范围之内的节点对,利用超声波六元阵进行TDOA测距可以直接测得距离值,从而可构造信息不完全的距离矩阵DN=[dij]N×N。利用节点间的欧式距离dij作为测地距离的替代,对已知距离值令dG(i,j)=d (i,j),用min{dG(i,j),dG(i,k)+dG(k,j)}替换dG(i,j),获得信息不完全的测地距离矩阵;然后,对于不在彼此通信范围之内的节点对,则通过最短路径算法(Dijkstra或Floyd算法)获得节点对之间的最短路径测地距离。收集所有节点对之间的距离值构成测地距离矩阵DG,然后就可以进一步计算网络相对坐标。
2.2 计算相对坐标
基于测地距离矩阵DG,对其应用古典MDS算法,即可构建网络相对坐标。这个过程如下:
(1)根据测地距离矩阵DG的数据,按照式(4)计算出bij:

(2)根据bij构造出X的中心化内积矩阵B:
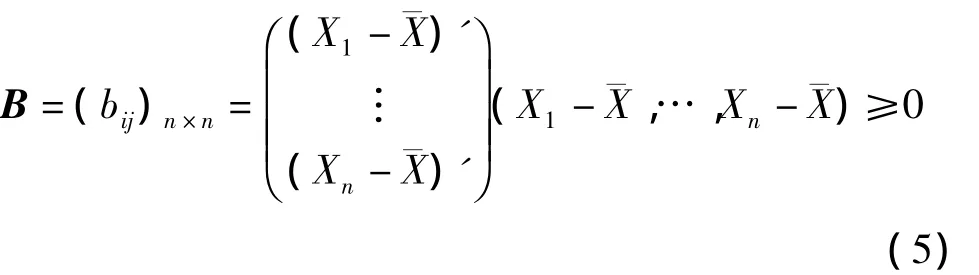
(3)记r为空间维度(此处默认为2维)λ1≥λ2≥…≥λr为B的正特征根,λ1,λ2,…,λr对应的单位特征向量为e1,e2,…,er,Γ=(e1,e2,…,er)是单位特征向量为列组成的矩阵,则,X矩阵中每一行对应空间中的一个点,第i行即为Xi。令Λ=diag(λ1,λ2,…,λr),那么式(5)可变为式((6):

(4)计算内积矩阵B的特征值λ1≥λ2≥…≥λn和r个最大特征值λ1≥λ2≥…≥λr>0对应的单位特征向量Γ。
(5)根据式(7)计算^X,得到网络相对坐标图。

2.3 计算绝对坐标
经过前面两步得到全网相对坐标,给出了每个节点的相对位置。虽然这些节点之间的相对位置关系是准确的,但是整个网络的坐标相对于真实位置则可能经过了缩放、旋转和翻转。为了获得网络绝对坐标,本文利用已知的锚节点构造坐标转换函数,将相对坐标图进行线性变换,使经过变换计算得到的坐标与锚节点的真实位置之间的误差平方总和最小,即更接近真实位置。
设坐标变换函数Q的系数矩阵为α,常数矩阵为β,则有:
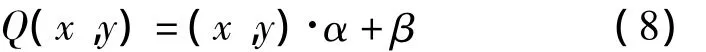
在2维空间中已知锚节点条件下,仅需选择3个锚节点M(b1,b2,b3),将其相对坐标上式求解齐次线性方程组,可得方程(8)的系数矩阵及常数矩阵β=(β1β2),从而得到坐标变换函数Q。利用上面获得的坐标转换函数,即可将相对坐标矩阵转换为绝对坐标矩阵。
3 仿真实验与分析
为了验证算法的有效性,本文在MATLAB仿真平台下,在30 m×30 m的二维场景中随机部署20个节点进行仿真实验,将本文提出的基于超声波六元阵列测距的测地距离多维定标定位算法(Geodesic Distance MDS)与Cricket所采用的迭代三边定位算法(Trilateration)以及AHLoS的迭代多点定位算法(Multilateration)进行仿真实验对比。由于本文设计的超声波六元阵最大可实现15 m范围内的测距,因此在MATLAB下定义节点间的测距范围为15 m,在测试结果中加入均值为零的高斯白噪声:
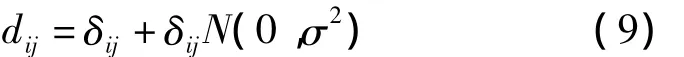
其中δij为真实距离,N(0,σ2)表示均值为0、方差为σ2的独立正态随机变量。仿真实验中以超声波六元阵TDOA测距实验得到的平均相对测距误差作为参考,将平均相对测距误差σ设为0.4%和1.5%分别进行实验。
定位算法的性能通过平均定位估计误差计算:
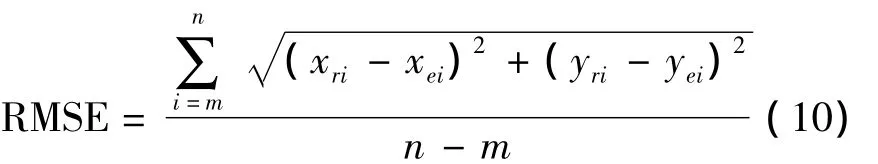
其中xri,yri表示i的真实坐标,xei,yei表示算法估计坐标。通常该误差越低定位算法性能越好。
在σ设为0.4%和1.5%时分别进行实验,按照不同节点规模将3种定位算法进行实验,计算定位误差并进行对比,其结果分别如图5和图6所示。
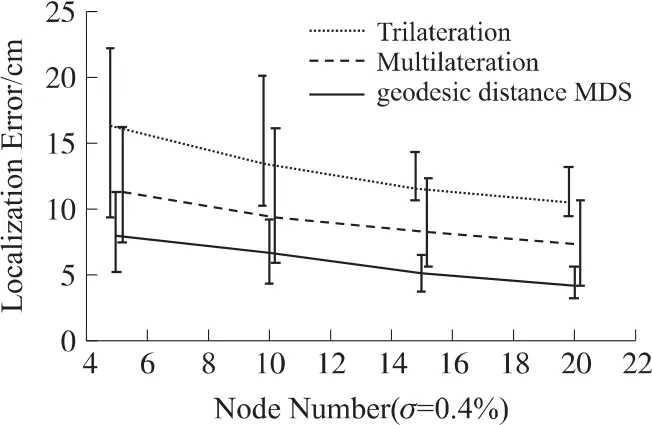
图5 不同节点数量下定位结果误差对比(σ=0.4%)
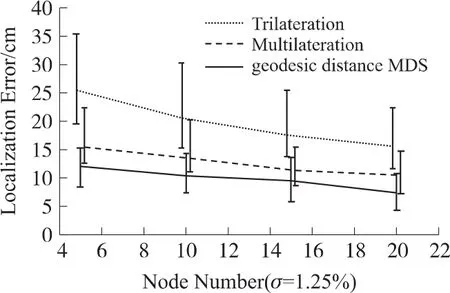
图6 不同节点数量下定位结果误差对比(σ=1.5%)
仿真实验表明,3种算法的定位误差随着测距误差的降低和节点密度的增加而有所降低。但与三边定位(Trilateration)和多点定位(Multilateration)算法相比,Geodesic Distance MDS算法能够准确构建距离矩阵,获得精确的相对关系,从而获得更高的定位精度,定位误差分别降低50%和30%以上,定位误差可降低到10 cm以内。在测距误差较小,节点数量多,网络平均连通度较高的情况下,算法能够获得更为准确的距离矩阵,从而获得较高的定位精度;而当节点数量较少,网络连通度不高时,部分距离信息采用最短路径替代,因而也会存在一定误差,但相比其他两种算法其误差则小得多。
4 结论
本文研究了基于超声波六元阵列TDOA测距的WSN网络节点定位技术。超声波测距系统采用RF信号实现收发节点同步,用温度补偿和软件处理延迟的方法有效减少误差,提高测距精度。在15 m范围内,室内测距的平均误差为8 cm,最大误差为26.7 cm。在此基础上提出一种测地距离的多维定标定位算法实现WSN精确定位。本文以超声波六元阵测距实验取得的测距精度作为依据,在MATLAB平台下对定位算法进行了仿真实验,结果表明Geodesic Distance MDS算法比迭代三边定位和迭代多点定位等方法定位精度更高,定位误差分别降低50%和30%以上,可满足较大范围定位需求。
[1]吴凌飞,孟庆虎,梁华为,等.一种基于共线度的无线传感器网络定位算法[J].传感技术学报,2009,22(5):722-727.
[2]唐弢.基于锚节点的无线传感器网络定位技术研究[D].哈尔滨:哈尔滨工业大学,2013.
[3]方震,赵湛,郭鹏,等.基于RSSI测距分析[J].传感技术学报,2007,20(11):2526-2530.
[4]刘世森,汤朝明,吴畏.无线传感器网络中的TOA测距方法研究[J].工矿自动化,2012.192(38):36-39.
[5]赵海,张宽,朱剑,等.基于TDOA的超声波测距误差分析与改进[J].东北大学学报(自然科学版),2011(6):802-805.
[6]常华伟,王福豹,严国强,等.无线传感器网络的TOF测距方法研究[J].现代电子技术,2011,34(1):35-38.
[7]Shang Y,Ruml W,Zhang Y.Localization from Connectivity in Sensor Networks[J].IEEE Trans on Parallel and Distributed Systems,2004,15(11):961-973.
[8]Liu K Z,Yan X P,Hu F P.A Modified DV-Hop Localization Algorithm for Wireless Sensor Networks[C]//IEEE International Conference on Intelligent Computing and Intelligent Systems.Shanghai,China,2009:511-514.
[9]陈岁生,卢建刚,楼晓春.基于MDS-MAP和非线性滤波的WSN定位算法[J].浙江大学学报(工学版),2012,46(5):866-872.
[10]Nissanka Bodhi Priyantha.The Cricket Indoor Location System[D].Massachusetts Institute of Technology,2005.
[11]Andreas Savvides,Chih-Chieh Han,Mani B Strivastava.Dynamic Fine-Grained Localization in Ad-Hoc Networks of Sensors[J].Proceedings of the 7th Annual International Conference on Mobile Computing and Networking,2001:166-179.
[12]Georg Oberholzer,Philipp Sommer,Roger Wattenhofer.SpiderBat: Augmenting Wireless Sensor Networks with Distance and Angle Information[C]//IPSN’11,April 12-14,2011,Chicago,Illinois.
[13]Shang Y,Ruml W,Zhang Y,et al.Localization from Mere Connectivity in Sensor Networks[C]//Proc of the 4th ACM Int’l Symp on Mobile Ad Hoc Networking and Computing.New York:ACM Press,2003:201-212.
[14]黄洁,王福豹,段渭军.WSN节点超声波测距技术研究[J].电子设计工程,2013,21(6):120-122.

赵晴晴(1989-),女,山东德州人,硕士生,主要研究方向为无线传感器网络,zhaoqingqing0413@163.com;

黄亮(1985-),男,湖北孝感人,博士生,主要研究方向为传感器网络、无线adhoc网络等,huangliangnumber1 @163.com;

段渭军(1962-),男,陕西渭南人,研究员,硕士生导师,主要研究方向为无线传感器网络、信号处理,duanwj@nwpu. edu.cn。
基于超声波六元阵列测距的WSN节点定位技术研究*
赵晴晴,黄亮,傅贤锋,李明远,段渭军*
(西北工业大学电子信息学院,西安710072)
基于超声波测距的定位技术以其精度高、范围广和性能稳定等优点,在无线传感器网络中广泛应用。为了实现较大范围的高精度定位,利用自主实现的超声波六元传感器阵列进行TDOA测距,并进行测距误差分析,然后采用基于测地距离的多维定标算法(Geodesic Distance MDS)进行无线传感器网络节点定位。在MATLAB平台下与Cricket采用的迭代式三边定位和AHLoS采用的多点定位算法进行对比仿真实验,结果表明Geodesic Distance MDS算法在不同网络规模和测距误差条件下均能够获得更高的定位精度和较小的定位误差。
无线传感器网络;超声波六元阵测距;多维定标;到达时间差;节点自定位
TP393
A
1004-1699(2014)03-0368-05
2014-01-20修改日期:2014-03-07
C:6150P
10.3969/j.issn.1004-1699.2014.03.018
项目来源:西安市科技计划项目(CX1255①)
猜你喜欢
杂志排行
传感技术学报的其它文章
- Design and Implementation for Diarrheic Shellfish Poison Detection Based on Electrical Cell-Substrate Impedance Sensing*
- A Design of ECG Signal Monitoring System Based on Intelligent Terminal
- A Study of Multi-Channel sEMG De-Noising and Aliasing Removal*
- Analysis of Temperature Characteristic and Design of Interface ASIC Based on Ring Schottky Diode for MEMS Gyroscope*
- Fabrication and Characteration of NiCr-NiSi Thin Film Thermocouples on CFCC-SiC Substrate*
- Fluxgate Magnetometer with Low-Cost and High-Resolution Based on ARM*
