The purification scheme ofmultiphoton entanglement state based on quantum nondemolition (QND)measurement
2014-09-08YANFeiHUANGFeng
YAN Fei,HUANG Feng
(Department of Mathematics and Physics,Anhui Jianzhu University,Hefei 230601,China)
The purification scheme ofmultiphoton entanglement state based on quantum nondemolition (QND)measurement
YAN Fei,HUANG Feng
(Department of Mathematics and Physics,Anhui Jianzhu University,Hefei 230601,China)
Based on quantum nondemolition(QND)measurements of photon numbers,a multiphoton polarization entanglement purification scheme was proposed in this paper.Because the W state was the basis vector of the new mixed tripartite entangled state,we called it the mixed W state.Here,the QND detectors acted not only as the CNOT operations but as single photon number detectors.Itwould greatly reduce the complexity of the realization of the purification scheme.All thesemerits suggested that the purification scheme for themixed W states could be realized with the current technology.
quantum nondemolition measurement;mixed W state;cross-Kerr nonlinearity; quantum purification
0 Introduction
Entanglement presented by Schrodinger is a criticalmanifestation of quantum mechanics.During the past years,quantum entanglement played a more and more important role in quantum information processing and transmission,such as quantum cryptography[1-4],quantum teleportation[5],quantum dense coding[6],and so on.In quantum communication,entanglement states are used to build quantum channel for information transmission.However,due to the impossibility thatone quantum system can be isolated from the environment absolutely,the noise in quantum channelwill inevitably degrade the entanglement of quantum system,and the practically available quantum entangled states are all nonmaximally entangled states,even the mixed states.So,if nothing has been done on the distributed states before used in quantum communication,the reduced entanglement of quantum system will decrease the fidelity of quantum teleportation or make quantum communication insecure.To overcome this problem,many schemes have been proposed,such as entanglement distillation[7-8]entanglement concentration[9-10],and entanglement purification[11].Entanglement purification is amethod that can extract a small number of entangled pairs with a relatively high degree of entanglement from a large number of less entangled pairs using only local operations and classical communication(LOCC),while entanglement concentration is the process to obtain somemaximally entangled states from a set of pure non-maximally entangled states.In the original entanglement purification scheme[11],Bennett et al proposed a protocol for increasing the entanglement of quantum systems in a Werner state with Controlled-not gates (CNOT)and single partitlemeasurements.But,in experiment,it is difficult to implement a perfect CNOT operation[12].Subsequently,various schemes of entanglement purification have been proposed[13],and many of them were focusing on how to avoid the difficult CNOT operation.In 2001,Pan et al[14]presented an experimental protocol for the entanglement purification of photon pair by using the ordinary polarized beam splitter rather than the original complicated CNOT operation.This proposal has been realized in Lab in 2003[15].Recently,Sheng et al[16]introduced a scheme for polarization-entanglement purification based on parametric down-conversion sources with cross-Kerr nonlinearity.Subsequently,they introduced a deterministic entanglement purification protocol for two-photon entangled states[17].In 2011,Deng proposed an economical one-step error-correction protocols for multipartite polarization-entangled systems[18]and efficientmultipartite entanglement purification with entanglement link from subspace in a GHZ state[19].
From the previous entanglement purification schemes,we find that most of them are working on the bipartite entanglement purification.There are few proposals discussingmulti-qubit entanglement purification.In 1998,Murao et al[20]proposed amultipartite purfication protocol bymeans of local operations and classical communication.The high dimensional purification protocol also has been proposed by Cheong et al[21].However the entanglement of three qubits is more complicated than that of two qubits.Recently,Sheng et al[22]presented an entanglement purification protocol for a multipartite GHZ state with QNDs.In 2011,based on charge detection amultipartite electronic entanglement purification was proposed[23].Because GHZ state can be regarded as themaximally entangled state of three qubits.If one of the three qubits is traced out,the remaining state is completely unentangled.Thus,the entanglement properties of the GHZ state are very fragile under particle losses.However,W state hasmore robust entanglement than GHZ state[24]in the sense that the remaining two particles are still in an entangled state if the third one is traced out.Inspired by Sheng et al[22]proposal,in this paper,we will propose an entanglement purification scheme for the mixed triphoton polarized entangled states,which is expressed as themixture ofW-type and GHZ-type basis states.Because these two types of entangled states are genuine tripartite entangled states,we call this kind of basis the genuine basis[25].
QND has the potential available of being able to condition the evolution of the system without necessarilydestroying the single photons[26-28].The QND device is generally composed of several cross-Kerr nonlinearities,a probe beam,several polarized beam splitters(PBSs)and the X homodynemeasurement.The Hamiltonian[26]of the cross-Kerr nonlinearity is
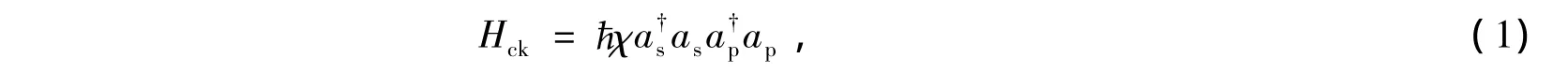
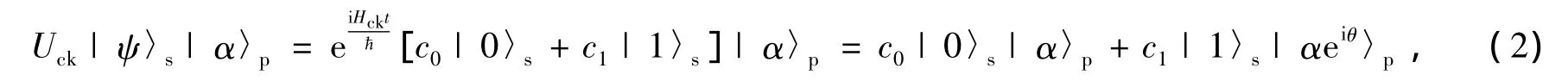
whereθ=χt and t is the interaction time.It is shown in the Eq.(2)that the Fock state|n〉sis unaffected by the interaction but the coherent laser probe beam|α〉picks up a phase shift directly proportional to the number of the photons in the Fock state.Namely,for n,n=0;1 photons in the signalmode,the probe beam evolves to|αeinθ〉p.
Fig.1 is Schematic diagram showing the principle of the QND detector.In Fig.1,two coss-Kerr nonlinearities and a coherent laser probe beam|α〉are used in our protocol.θrepresents the cross-Kerr nonlinearities that induce a phase shift on the probe beam.The QND can distinguish superpositions and mixtures of the states|HH〉and|VV〉from|HV〉and|VH〉.This two-qubit QND detector is a parity checking device.
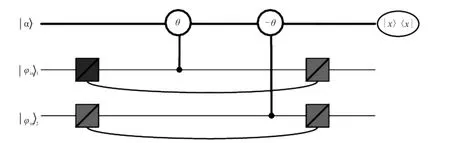
Fig.1 Schematic diagram show ing the princip le of the QND detector
1 Multipartite entanglement purification via QNDs
1.1 Quantum nondemolition measurements and the genuine basis for tripartite systems
We consider two polarization qubits initially prepared in the states|φ〉1=c0|H〉1+c1|V〉1and |φ〉2=d0|H〉2+d1|V〉2where|H〉and|V〉are two independent polarizations of the photons.The principle of the nondestructive quantum nondemolition measurement of the photon number state is shown in Fig.1.One can easily see that|HH〉and|VV〉pick up no phase shift and remain coherent with respect to each other.The probe beam|α〉pwill pick up a phase shiftθ(-θ)if the state is|HV〉(|VH〉).Sowe can distinguish superpositions and mixtures of the states|HH〉and|VV〉from|HV〉and|VH〉using s a coherent state|α〉probe beam and several cross-Kerr nonlinear interactions.Namely the state of the signal-probe combined system|φ〉1|φ〉2|α〉pwill evolve to


here the tripartite|W〉i(i=1,…,8)of A,B and C are shared by Alice,Bob and Charlie,respectively.
We will use the generic basis labels|0〉and|1〉representing|H〉and|V〉,respectively.
Following the Refs.[22,25-26],in this paperwewill propose a scheme for entanglement purfication of three qubits quantum system.The state to be purfied is a tri-photonmixed polarized entangled states,which is expressed by themixed W state[25],and the purification process ismainly based on the QND detector as depicted in Fig.2.
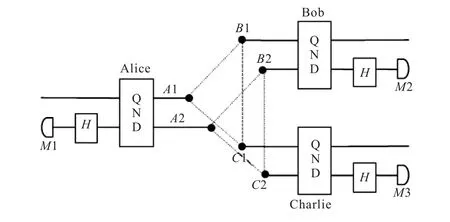
Fig.2 Schematic diagram show ing the principle of the tri-photon polarization entanglement purification protocol w ith QND detectors
In Fig.2,the rotation H represents a Hadamard operation.M is the single photon measurement for the states of down spatialmode.
1.2 Purification ofmixed W state based on QNDs
During the transmission process,entanglement will inevitably degrade.For communication purpose,suppose the three distant users Alice,Bob and Charlie share an ensemble ofρafter the transmission as
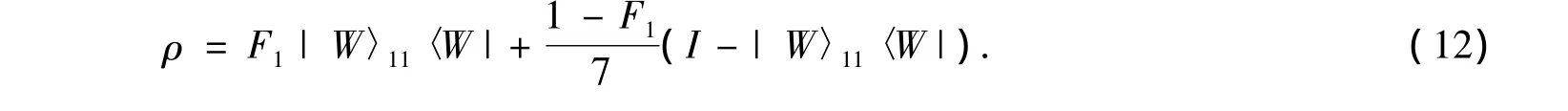
Here,to simplify the calculation,without loss of generality,we have let Fi=,i=2,3,…,8.Fiis unknown coficient and Fiis the fidelity relative to the ideal|W〉1state.
In order to complete the purification process,the three users must divide the ensemble of quantum systems intomany groups and the state of each group can be described by Eq.(12).We denote two pairs of them as A1B1C1and A2B2C2.So the total state of the system before purification can be viewed as a probabilisticmixture of 64 pure states,i.e.,|W〉1|W〉1,with a probability of,|W〉i|W〉jwith a probability ofif i=1,j≠1 and j=1,i≠1,and|W〉i|W〉j,with a probability ofif i,j≠1,respectively.
Each user,say Alice lets her two photons A1and A2pass through the up spatialmode and the down spatial mode,respectively,as shown in Fig.2.So do the other users Bob and Charlie.After the QNDs,the three parties compare their photons.If Alice,Bob and Charlie get the same results with an X homodyne measurement,after these operations,the quantum systems are in a new mixture of the following states
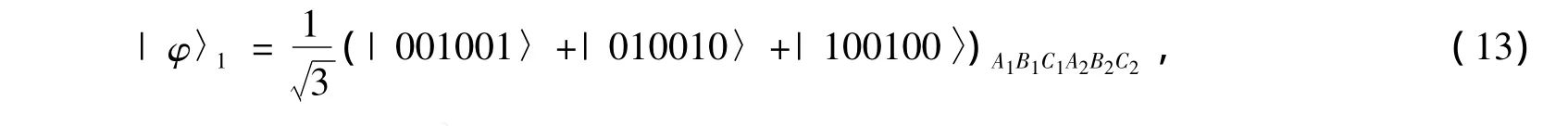
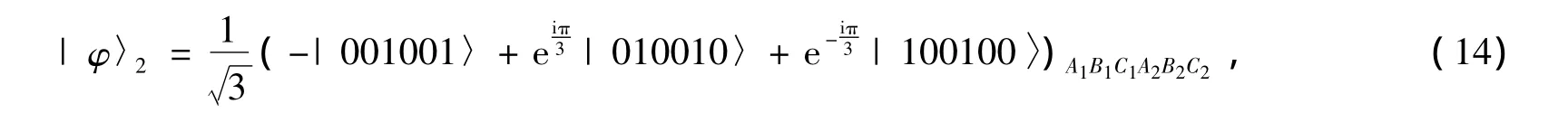
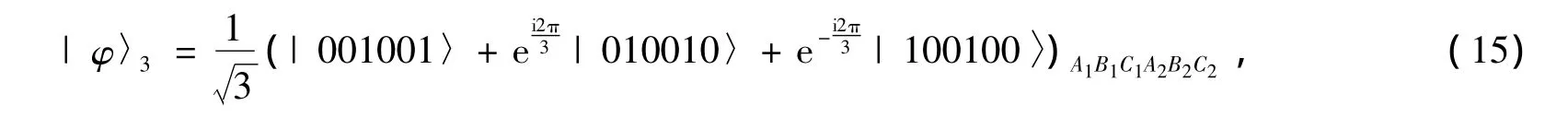
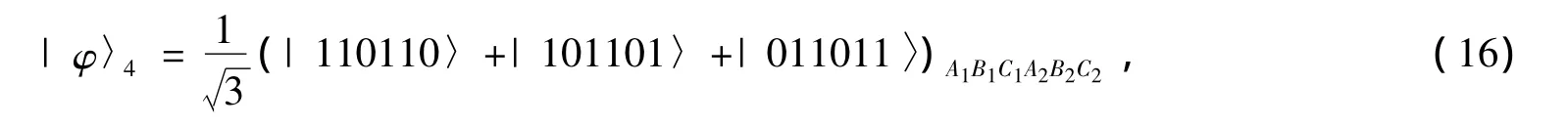
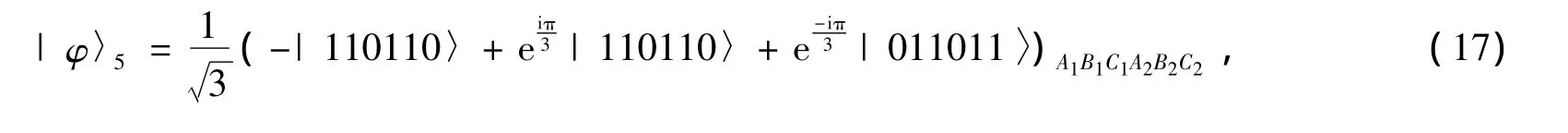
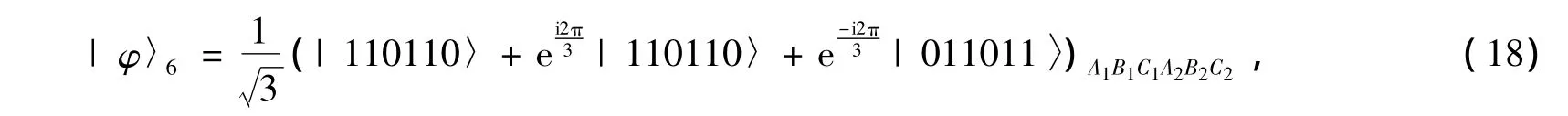
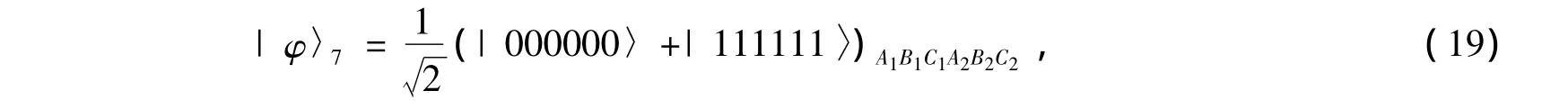
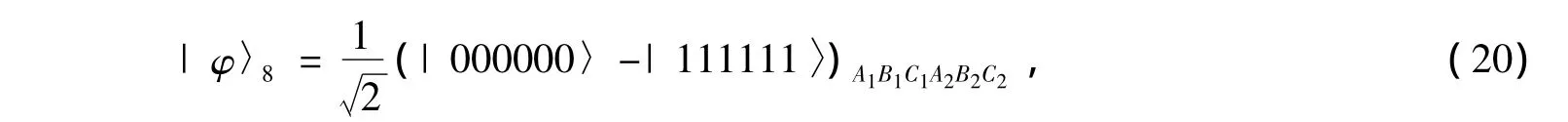
After the rotation R45on each photon in the down spatialmode as shown in Fig.2(the rotation operation completes the transformalions|0〉→(|0〉+|1〉→(|0〉-|1〉,themeasurementoutcome of the parties A2B2C2and the states of quantum system A1B1C1are shown in Tab.1.In the table,for example,σZ(A1)is the phase-flip operator,i.e.,|0〉→|0〉and|1〉→-|1〉on qubit A1.

Tab.1 The states of photons A1,B1and C1and the corresponding unitary transformations conditioned on themeasurement results on A2,B2and C2
So after these operations,the new fidelity is F'1=If the value of F'1,the fidelity will be enhanced,namely F'1-F1>0.That is to say we have accomplished the entanglement purification task with QNDs.
2 Conclusion
In summary,we present an entanglement purification protocol for tri-photon mixed entangled states expressed in the new genuine tripartite basis-mixed W states by using quantum nondemolition detectors.Here,the QND is realized by a coherent probe beam and several cross-Kerr nonlinear interactions between the signal beams and the probe beam.In our protocol,the QND detectors act not only as the CNOT operations but as single photon number detectors.The results show that,this QNDs-based purification protocol works fine for themixed tri-photonW states.With the help of QND technique,the complicated CNOT operations are no longer needed in the current entanglement purification scheme,whichmakes itmore feasible.So our protocol may be a useful scheme in long distance quantum communication.
[1]Ekert A K.Quantum cryptography based on Bell's theorem[J].Phys Rev Lett,1991,67:661-663.
[2]Bennett CH,Brassard G,Mermin N D.Quantum cryptography without Bell's theorem[J].Phys Rev Lett,1992,68: 557-559.
[3]Gisin N,Ribordy G,TittelW,et al.Quantum cryptography[J].Rev Mod Phys,2002,74:145-195.
[4]Deng FG,Long G L.Controlled order rearrangement encryption for quantum key distribution[J].Phys Rev A,2003,68:042315.
[5]Bennett C H,Brassard G,Crepeau C,etal.Teleporting an unknown quantum state via dual classicaland Einstein-Podolsky-Rosen channels[J].Phys Rev Lett,1993,70:1895-1899.
[6]Bennett C H,Wiesner S J.Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states[J].Phys Rev Lett,1992,69:2881-2884.
[7]Kwait PG,Barraza-Lopez S,Stefanov A,et al.Experimental entanglement distillation and‘hidden’non-locality[J].Nature(London),2001,409:1014-1017.
[8]Opatrnay T,KurizkiG.Optimization approach to entanglement distillation[J].Phys Rev A,1999,60:167-172.
[9]Bennett C H,Bernstein H J,Popescu S,etal.Concentrating partial entanglementby local operations[J].Phys Rev A,1996,53:2046-2052.
[10]Bose S,Vedral V,Knight P L.Purification via entanglement swapping and conserved entanglement[J].Phys Rev A,1999,60:194-197.
[11]Bennett C H,Brassard G,Popescu S,et al.Purification of noisy entanglement and faithful teleportation via noisy Channels[J].Phys Rev Lett,1996,76:722-725.
[12]Briegel H J,Duer W,Cirac J I,et al.Quantum repeaters:the role of imperfect local operations in quantum communication[J].Phys Rev Lett,1998,81:5932-5935.
[13]Ho K H,Chau H F.Purifying Greenberger-Horne-Zeilinger states using degenerate quantum codes[J].Phys Rev A,2008,78:042329.
[14]Pan JW,Simon C,Brukner C,et al.Entanglement purification for quantum communi-cation[J].Nature (London),2001,410:1067-1070.
[15]Pan JW,Gasparoni S,Ursin R,et al.Experimental entanglement purification of arbitrary unknown states[J].Nature(London),2003,423:417-422.
[16]Sheng Y B,Deng F G,Zhou H Y.Efficient polarization-entanglement purification based on parametric downconversion sources with cross-Kerr nonlinearity[J].Phys Rev A,2008,77:042308.
[17]Sheng Y B,Deng F G.Deterministic entanglement purification and complete nonlocal Bell-state analysis with hyperentanglement[J].Phys Rev A,2010,81:032307.
[18]Deng FG.One-step error correction formultipartite polarization entanglement[J].Phys Rev A,2011,83:062316.
[19]Deng FG.Efficientmultipartite entanglement purification with entanglement link from subspace[J].Phys Rev A,2011,84:052312.
[20]Murao M,Plenio M B,Popescu S,et al.Multiparticle entanglement purification protocols[J].Phys Rev A,1998,57:R4075-R4077.
[21]Cheong Y W,Lee SW,Lee J,et al.Entanglement purification for high-dimensionalmultipartite systems[J].Phys Rev A,2007,76:042314.
[22]Sheng Y B,Deng F G,Zhao B K,et al.Multipartite entanglement purification with quantum nondemolition detectors[J].Eur Phys JD,2009,55:235-242.
[23]Sheng Y B,Deng FG,Long G L.Multipartite electronic entanglement purification with charge detection[J].Phys Lett A,2010,375:396-400.
[24]Eibl M,Kiesel N,Bourennane M,et al.Experimental realization of a three-qubit entangled W state[J].Phys Rev Lett,2004,92:077901.
[25]Yang M,Yan F,Cao Z L.Purification ofmultipartite entanglementby local operations[EB/OL].(2009-04-15)[2013-08-20]http://arxiv.org/abs/0904.2343.
[26]Nemoto K,MunroW J.A near deterministic linear optical CNOT gate[J].Phys Rev Lett,2004,93:250502.
[27]Milburn G J,Walls D F.State reduction in quantum-counting quantum nondemolition measurements[J].Phys Rev A,1984,30:56-60.
[28]Grangier P,Levenson JA,Poizat JP.Quantum non-demolition measurements in optics[J]Nature(London),1998,396:537-542.
(责任编辑 郑小虎)
非破坏测量的多粒子纠缠纯化方案
严飞,黄凤
(安徽建筑大学数理系,安徽合肥230601)
提出了一种基于非破坏测量的多粒子纠缠混合态纯化方案.由于W态是该混合纠缠态的基本组成元素,所以称之为混合W纠缠态.利用交叉克尔非线性介质的宇称检测功能和光子计数功能,实现了无须联合Bell态测量和复杂的单光子探测技术的混合W态纠缠纯化方案,从而降低了纠缠纯化的复杂性,有利于实现纠缠纯化过程.
量子非破坏测量;混合W态;交叉克尔非线性效应;量子纯化
A
1000-2162(2014)04-0045-07
10.3969/j.issn.1000-2162.2014.04.008
Received date:2013-09-05
Supported by National Natural Science Foundation of China(10704001,61073048,10905024,11005029);the Key Project of Chinese Ministry of Education(210092);the China Postdoctoral Science Foundation (20110490825);the Key Program of the Education Department of Anhui Province(KJ2012A020,KJ2010A287,KJ2014A046,2010SQRL153ZD);the Doctoral Research Foundation of Anhui Jianzhu University(K02630);the“211 Project”of Anhui University(33190019);the Personnel Departmentof AnhuiProvince;Anhui Key Laboratory of Information Materials and Devices (Anhui University)
Author's brief:YAN Fei(1985—),male,born in Lujiang of Anhui Province,lecturer of Anhui Jianzhu University,Ph.D.
CLC number:O413
