一种基于Laplace谱的形状匹配算法

唐 俊，刘志忠，周洪伟，阚海俊

形状匹配是计算机视觉、图像分析和模式识别等领域中的一个关键问题.形状可以用点、线段、曲线等不同层次的几何基元来表示，但任何层次的几何基元都可离散为一系列的点，所以用点模式描述形状更具有普适性.因此，基于谱图理论的点模式匹配问题受到了极大关注.Scott等［1］首次将谱理论引入对应估计问题中，使用高斯加权函数构造待匹配特征点集间的邻接矩阵，然后对邻接矩阵进行SVD分解，通过比较得到的有序特征向量，求解点集间的匹配关系，此方法能处理大小不同的点集，但当点集间有较大旋转和缩放时，匹配效果不佳.针对Scott算法的缺陷，Shapiro等［2］提出了一种改进算法，分别构造两个点集内的邻接矩阵，并对邻接矩阵进行SVD分解，通过比较模态矩阵确定匹配关系;此算法对随机点抖动、仿射变换和缩放具有很好的鲁棒性，但该算法要求待匹配点集的大小相同.Carcassoni等［3］采取分层方法来抑制结构性差异在匹配中的影响.王年等［4］提出了一种基于Laplace谱的点模式匹配算法，该算法首先为两个特征点集分别定义了Laplace矩阵，随后对矩阵进行SVD分解，并根据特征向量间的距离确定匹配关系.Tang等［5］为进一步提高鲁棒性，提出将Laplace谱和双随机矩阵嵌入迭代变换与对应估计的框架中，以此确定匹配关系.Wang等［6］提出利用核主成分分析算法解决点模式匹配问题，该算法具有很好的抗离群点和抗随机抖动的能力.Leordeanu等［7］提出了基于成对约束的谱匹配算法，该算法能实现大小不同点集间的匹配，并在等距变换下可获得较好的匹配结果.赵健等［8］提出了一种新的不变量——相对形状上下文，并将其与谱方法结合，解决了Leordeanu算法在相似变换下匹配效果较差的问题.唐俊等［9］利用概率松弛方法，将形状上下文与Laplace谱相结合以优化匹配结果.文献［1－9］的方法在处理形状匹配时，并没有考虑形状本身的结构特性，得到的匹配结果并不一定是最优的.Thayananthan等［10］提出将形状轮廓的连续信息和弯曲信息同形状上下文相结合，以提升抗离群点的能力，并利用Viterbi算法求得联合代价函数的最小值，进而确定匹配关系，该算法在旋转角度不大的情况下能获得较好的匹配结果.

为了进一步提升匹配精度，并具有旋转不变性，作者提出一种新的形状匹配算法，首先定义两个形状的Laplace矩阵，并计算出对应的关系矩阵，然后将此矩阵代入Viterbi算法模型［12］，与形状的自身特性(弯曲能和邻接性［11］)相结合，从而得到更优的匹配结果.

1 Laplace谱匹配算法

设形状I包含n个特征点Ii(i=1，2，…，n)，定义Laplace矩阵如下

其中:d为任意两点的欧式距离.

对LI进行SVD分解，得到

其中:ΔI=diag(λ1，…，λm)，λ1≥ … ≥ λm－1＞ λm=0;U=(u1，…，um)为正交矩阵.

类似地，对于形状J可以得到

其中:ΔJ=diag{γi，…，γm}，V=(v1，…，vm).

当Cij同时为所在行与列的最大值时，说明I的第i个特征点与J的第j个特征点匹配.

2 结合结构信息的Laplace谱形状匹配算法

在形状匹配问题中，单独的Laplace谱算法得到的匹配结果往往并不可靠.为了提高准确率和鲁棒性，作者考虑将形状模型本身的结构特性(弯曲能和邻接性)融入对应估计中.函数f(·，·)表示两个特征点集间的对应关系，则总的匹配代价函数可写为

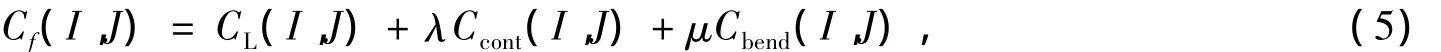
其中:CL为Laplace谱匹配代价，Ccont为邻接性代价，Cbend为弯曲能代价，λ和μ为权重参数.下面对上述符号作具体说明.

2.3 两组患者 BNP、COX-2、MMP-1、ACE2、TIMP-2水平比较 观察组患者BNP、COX-2、ACE2、TIMP-2水平高于对照组，MMP-1水平低于对照组，差异有统计学意义（P＜0.05）。见表2。

(1)Laplace谱匹配代价项CL

Laplace谱匹配代价项等于由函数f(·，·)所确定的所有对应点对的匹配代价之和，即

(2)邻接性代价项Ccont

邻接性约束是指在形状I中相邻的特征点Ii和Ik应与目标形状J中的相邻特征点Jf(i)和Jf(k)对应，其中函数f(i)表示将形状中的第i个点映射到目标形状中的第f(i)个点.假设Ii和Ii－1是相邻点，则邻接性约束可写成如下形式

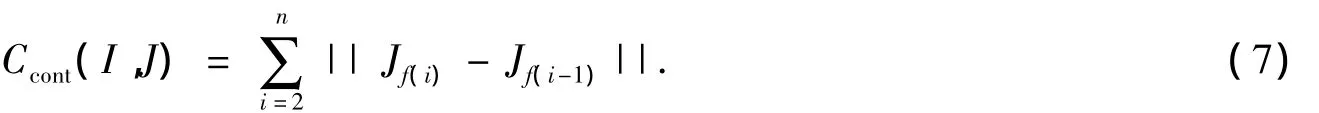
(3)弯曲能代价项Cbend

尖拐角或高曲率点具有高频特性，并且频率越高弯曲能也越高.因此，弯曲能可用于描述曲线的弯曲程度，且当曲线长度趋于无穷小时，弯曲能可作为点的局部特征.

设曲线为v(s)，则弯曲能等于曲线的曲率平方之和，即

其中:κ(i)=(v(i－1)+v(i+1)－2v(i))2表示第i个点的弯曲能.

如果两个特征点的弯曲能大小越相近，弯曲能代价项的值越小，那么两个特征点的局部特征越相似.弯曲能代价项可写成如下形式

Viterbi算法是十分有效的，它利用递归减少计算量，并使用整个序列的上下文来判断，从而即使观察序列中有一个“非寻常”的事件发生，也不会对结果产生很大影响.通常情况下，直接求解总代价函数的代价太高，为了简化运算，作者将对其中一个形状点集按顺(逆)时针进行排序，并利用Viterbi算法找出一条最优路径，从而确定形状点集间的匹配关系.

3 实验结果

3.1 性能分析

3.1.1 旋转不变性

点集中某一点的形状上下文［13］描述了其他点相对于该点的直方图分布，当选取不同的方向作为极坐标的正方向时，得到的形状上下文是不同的，因此形状上下文对旋转变换是非常敏感的.形状轮廓上某一点弯曲能的大小仅由当前点和其相邻两点共同决定，不随形状旋转而发生变化，具有旋转不变性.点间的邻接关系也不会因旋转而发生改变，同样具有旋转不变性，同时基于Laplace谱的匹配算法［5］(LP算法)在等距变换(平移、旋转和反射)下也是不变的.作者提出的算法是在LP算法的基础上，在对应估计过程中考虑了形状自身的结构信息，因此该文算法能获得更好的匹配结果，并具有旋转不变性.

3.1.2 复杂度分析

通过计算得到基于Laplace谱的初始匹配关系矩阵的复杂度为O(m3)，随后利用初始匹配关系矩阵及形状结构信息，在Viterbi模型上计算出匹配关系的复杂度为O(m3)，所以该文算法的复杂度为O(m3).

3.2 实验结果

在实验中，作者选取了不同的手势进行匹配，在每个手势轮廓上提取135个特征点.为验证可行性，将该文算法与LP算法和SCV算法［11］进行了比较.图1为不同手势的匹配结果，在一对手型中位置靠前的为原始手型，位置靠后的为目标手型，在每幅图中，都是将原始手型与目标手型进行匹配.图1中第1列为LP算法，第2列为SCV算法，第3列为该文算法，两手之间的连线表示错误匹配，位于手型边缘的方框中的“+”号交叉点表示未被匹配的点.

图1 不同手势的匹配结果Fig.1 The match results of different gestures

表1给出了多种算法不同手势的匹配结果比较.

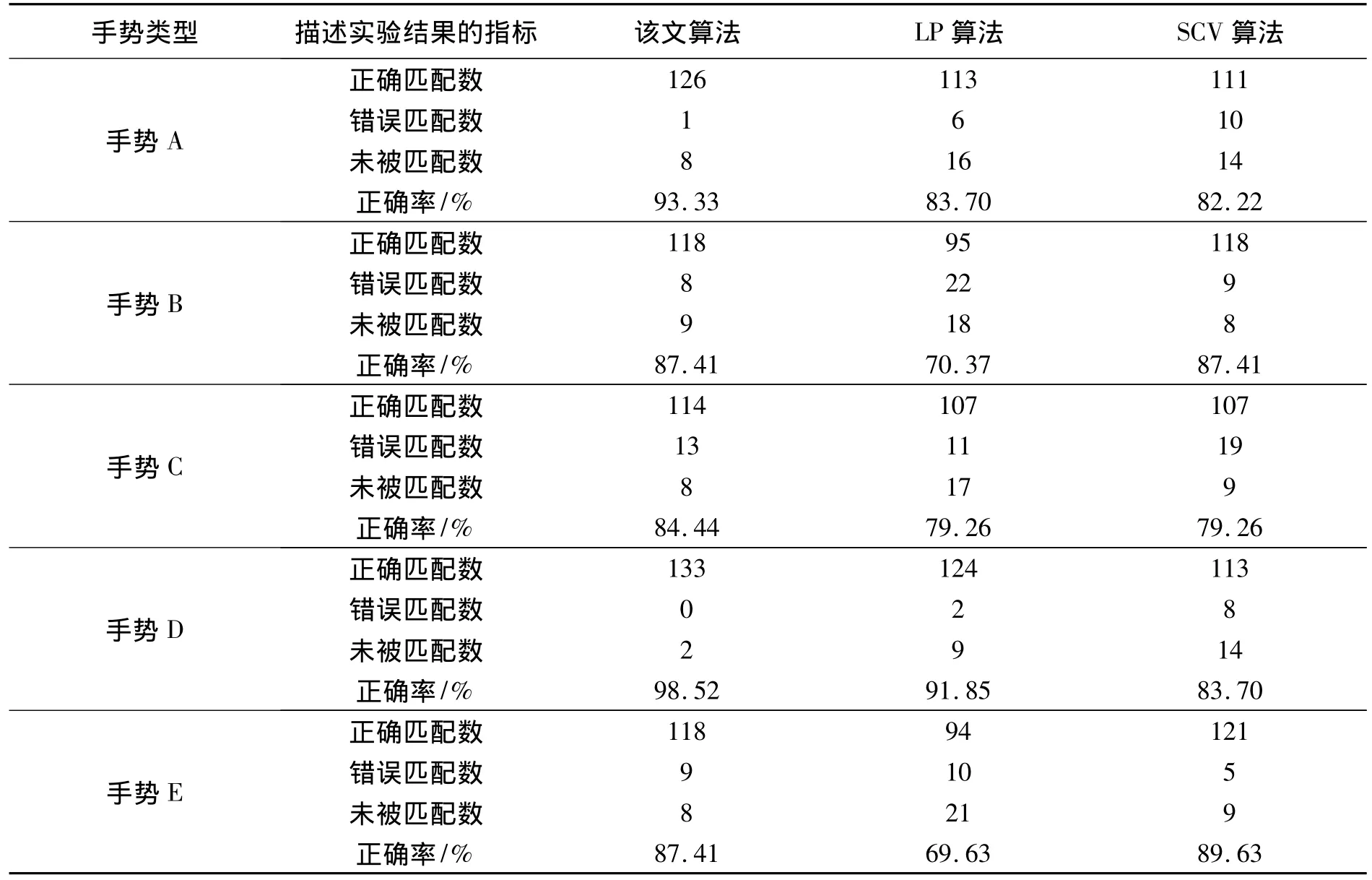
表1 多种算法不同手势匹配结果比较Tab.1 Comparison of the match results of different gestures with different algorithm

从表1可以看出，该文算法在正确匹配数和未匹配数方面均好于LP算法，而只有手势C中的错误匹配数稍多于LP算法;相对SCV算法，除了手势E外，该文算法在正确匹配数、未匹配数和错误匹配数方面均要好于SCV算法.SCV算法的一个致命弱点是不具备旋转不变性.对手势E进行5、10、15、30°的旋转，使用3种算法得到的实验结果如图2所示.图2中:一对手型中位置靠前的为原始手型，位置靠后的为目标手型，在每幅图中，都是将原始手型与目标手型进行匹配;第1列为LP算法，第2列为SCV算法，第3列为该文算法;两手之间的连线表示错误匹配，位于手型边缘的方框中的“+”号交叉点表示未被匹配的点.

图2 同一手势在旋转不同角度时的匹配结果Fig.2 The match results of the same gesture in different rotating angles

表2给出了多种算法同一手势在旋转不同角度时的匹配结果比较.

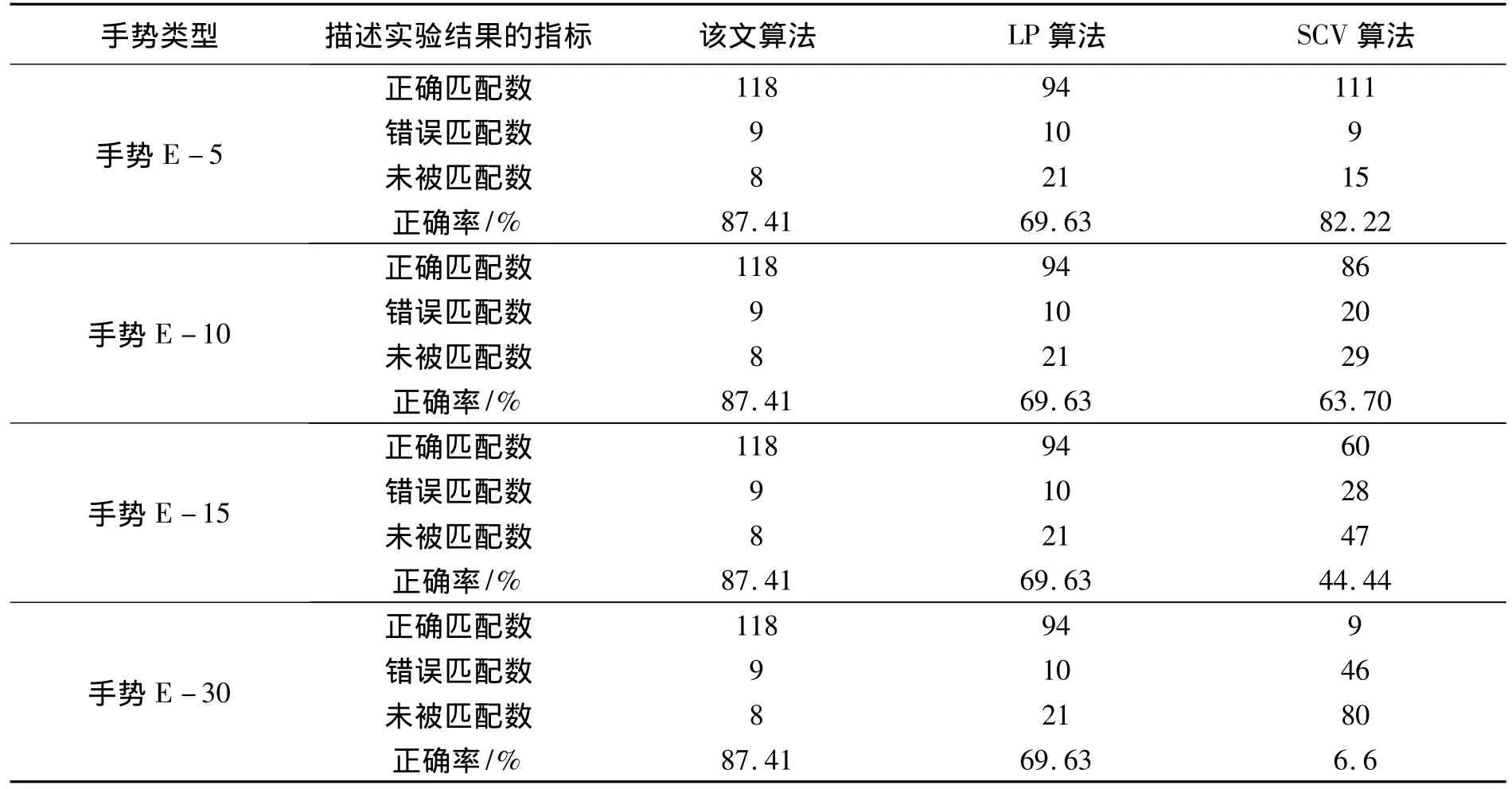
表2 同一手势在旋转不同角度时各算法的匹配结果比较Tab.2 Comparison of the match results of the same gesture in different rotating angles with different algorithms

从表2可以看出，在旋转变换下该文算法和LP算法的匹配结果不受旋转角度的影响，SCV算法随着旋转角度的增加，正确匹配率会急剧下降.

4 结束语

在形状匹配问题中，传统的谱算法只依据独立的特征进行分析，并没有考虑当前形状本身固有的特性，因此不能获得好的匹配结果.针对存在的问题，作者将形状本身的结构特性与Laplace谱算法相结合，提出了一种新的形状匹配算法，实现了形状的匹配，实验结果表明该文算法具有更高的准确性和较强的鲁棒性.

［1］ Scott G L，Longuet-Higgins H C.An algorithm for associating the features of two images［J］.Biological Sciences，1991，244:21 －26.

［2］ Shapiro L S，Brady J.Feature-based correspondence:an eigenvector approach［J］.Image and Vision Computing，1992，10(5):283 －288.

［3］ Carcassoni M，Hancock E R.Correspondence matching with modal clusters［J］.IEEE Pattern Analysis and Machine Intelligence，2003，25(12):1609 －1615.

［4］ 王年，范益政，韦穗，等.基于图的Laplace谱的特征匹配［J］.中国图象图形学报，2006，11(3):332－336.

［5］ Tang J，Liang D，Wang N，et al.A Laplace spectral method for stereo correspondence［J］.Pattern Recognition Letters，2007，28(12):1391 －1399.

［6］ Wang H F，Hancock E R.Correspondence matching using kernel principal components analysis and label consistency constraints［J］.Pattern Recognition，2006，39(6):1012 －1025.

［7］ Leordeanu M，Hebert M.A spectral technique for correspondence problems using pairwise constraints［C］∥Proceedings of the Tenth IEEE International Conference on Computer Vision，2005:1482 －1489.

［8］ 赵健，孙即祥，李智勇，等.基于相对形状上下文和谱匹配方法的点模式匹配算法［J］.电子与信息学报，2010，10(32):2287－2293.

［9］ 唐俊，王年，梁栋，等.一种结合形状上下文分析的Laplace谱匹配算法［J］.系统仿真学报，2009，14(21):4344－4350.

［10］ Thayananthan A，Stenger B，Torr P H S，et al.Shape context and chamfer matching in cluttered scenes［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，2003:127－133.

［11］ Kass M，Witkin A，Terzopoulos D.Snakes:active contour models［J］.International Journal of Computer Vision，1987，1(4):259 －268.

［12］ Forney G D.The viterbi algorithm［J］.Proceedings of the IEEE，1973，61(3):268 －278.

［13］ Belongie S，Malik J，Puzicha J.Shape matching and object recognition using shape contexts［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(4):509 －522.