单元方向图对阵列综合性能影响分析

丛友记，卢 青，简 玲

(中国船舶重工集团公司第七二四研究所，南京 211153)

单元方向图对阵列综合性能影响分析

丛友记，卢 青，简 玲

(中国船舶重工集团公司第七二四研究所，南京 211153)

在阵列天线综合问题中，传统方法假设各辐射单元各向同性且忽略互耦效应。工程应用中这些忽略会给计算结果带来较大的误差。本文首先建立了天线单元方向图对天线阵列性能影响的数学模型，对阵列指向精度、目标方向图赋形等问题进行了仿真对比分析。为了克服由单元方向图带来的误差，将阵中单元方向图代入优化过程中，算例表明该措施的有效性。考虑了阵列边缘单元辐射特性差异对阵列性能的影响。仿真结果表明在优化过程中考虑这些差异可以进一步提高计算精度。

单元方向图；阵列天线；阵列综合；赋形

0 引 言

相控阵体制雷达具有抗干扰能力强、搜索和跟踪目标快以及可靠性高等优势，是未来雷达的发展方向之一。如何实现相控阵天线各类的波束赋形是研制相控阵雷达面临的重要课题。阵列天线方向图综合包含低副瓣、超低副瓣方向图、各种赋形波束、展宽波束等功能的实现。经典的Chebyshev综合、Taylor综合等可用于笔形波束的综合。这些算法具有解析形式，计算速度快，但对于更加复杂的方向图赋形具有局限性。全局优化算法如遗传算法(GA)、粒子群(PSO)、模拟退火(SA)等可应用于不同间距、任意形状的阵元配置，其因通用性好且能够满足多种类型的方向图综合要求而得到了大量的应用。但是，这类数值算法随着变量数目的增大而计算量急剧增大，收敛缓慢，在大型阵列综合方面的应用受到了很大的限制。文献[1]采用了各类智能优化算法相结合的混合优化算法，在解决大型阵列综合问题上具有很大的优势。

本文首先建立了阵列天线方向图与辐射单元方向图关系的数学模型，从理论上分析了单元方向图对阵列性能的影响。接下来给出了单元方向图影响的具体实例，总结了一些规律，并给出修正措施。为了补偿单元方向图引起的误差，在阵列综合优化中代入了辐射单元方向图。最后还分析了由边缘效应带来的一些误差并给出了补偿方法。

1 数学模型

假定相控阵平面阵列中辐射单元按栅格状排列，且各单元匹配良好。如图1所示的x-y平面上K×L个辐射单元组成的矩形栅格平面阵列，设第(k,l)个辐射单元的激励电流值I(k,l)，阵中单元方向图为fkl(u,v)，则阵列方向图可以表示为[2]

(1)

式中

其中，dx和dy分别表示沿x和y方向上的单元间距；λ0为自由空间波长；I(k,l)=A(k,l)exp(jφ(k,l))，A(k,l)、φ(k,l)分别是阵列单元的幅度、相位。

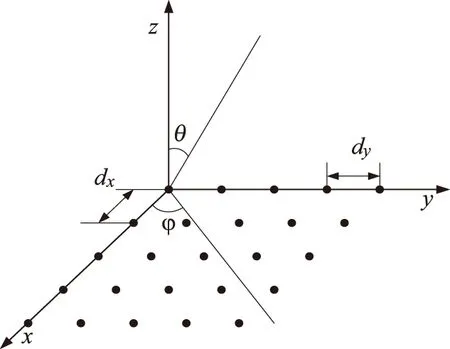
图1 平面阵列结构示意图

阵列综合就是找到一组阵列单元的幅度、相位分布，使式(1)计算出来的阵列方向图满足目标方向图。传统的阵列综合均假定单元方向图为全向且单元之间无互耦，即fkl(u,v)=1。在工程应用中，忽略单元方向图的影响会大大简化阵列综合流程，提高阵列综合的效率。实际中辐射单元方向图是各向异性的，且每个辐射单元的方向图由于加工误差、安装位置不同均会不同。忽略这些误差将会使优化结果的可靠性大大降低，由此需要对单元方向图的影响作进一步的研究。

2 设计实例

2.1 阵列指向精度

相控阵的波束指向是根据单元间距及波束指向对各个单元配相来实现的，在所需的波束指向上形成等相位面。假定单元行间距、列间距归一化波长分别为dy、dx，波束指向角度为(As,Es)，则第(m,n)单元的相位为

φmn=n*φx+m*φy

(2)

式中，φx=-2πdxcos(Es)sin(As)，φy=-2πdysin(Es)，阵列中各单元按照式(2)计算出来的相位配相。然而，式(2)所计算出来的相位分布并未考虑单元方向图的影响。实际上，由式(1)可知阵列方向图是单元方向图与阵因子两者共同的结果，或者说是单元方向图对阵因子进行调制作用的结果[3]。这样就会导致由式(2)计算的相位配置使阵列波束的指向与实际要求有所偏差。为了模拟这种偏差，本文对开口波导组成的一维线阵进行了仿真分析，如图2所示。

图2 开口波导16单元线阵示意图

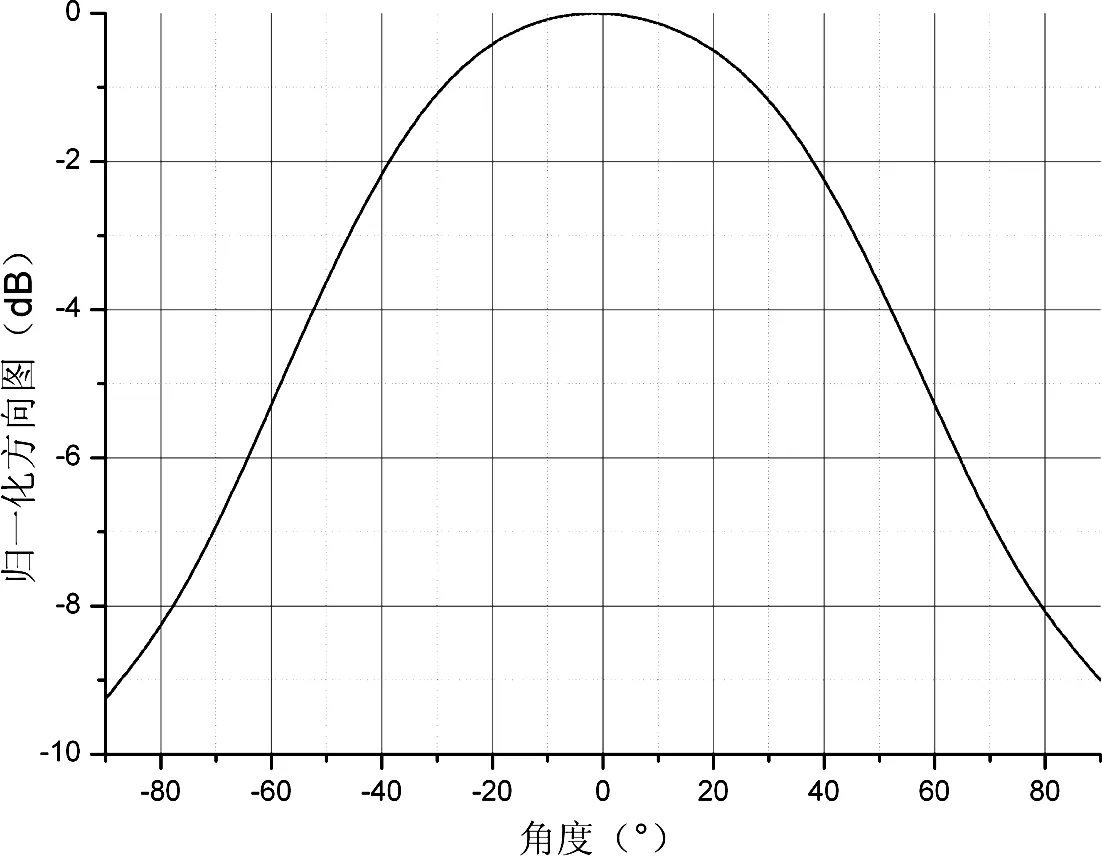
(a) 阵中单元E面方向图

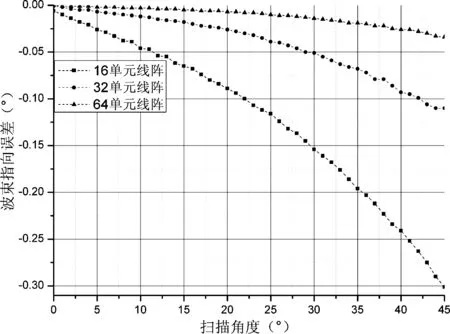
(b) 扫描误差曲线

本例分别对16、32、64单元的一维线阵进行了仿真分析，单元间距为0.6λ0。将式(2)计算的相位代入商用电磁仿真软件Ansoft HFSS[4]中求出实际全波仿真的波束指向，对波束指向偏差进行对比分析。图3给出了阵中单元方向图以及三类不同线阵的仿真结果对比。

从图3可以明显地看出单元方向图对阵列方向图的调制作用。当阵元数较少时，单元方向图对阵列波束指向影响较大，而随着阵列规模的增大，阵列方向图的指向误差将会减小。这是因为当阵列规模较小时，阵因子方向图波瓣较宽，单元方向图对阵因子的调制作用明显。随着阵列规模的增大，阵因子波瓣越来越窄，在阵列方向图中起主要作用的是阵因子，方向图的调制作用有限。为了消除该误差影响，可以根据实测结果与配相的关系反求所需波束指向的各单元配相。从图3还可以看出，阵中单元辐射方向图波瓣宽度不能太窄，否则阵列天线的波束扫描区域会受到限制。

2.2 45°余割平方波束综合

阵列综合的重要任务就是通过优化阵列中各辐射单元的幅度、相位以获得与目标方向图逼近的方向图。余割平方波束由于能够给不同斜距同一高度的目标提供均匀照射，兼顾了雷达的低空与高空的威力，是工程上常用的波束形式。因此，本文以45°余割平方波束赋形为例，在综合中将阵中单元方向图加入优化过程，并与传统的综合方法进行对比，讨论单元方向图对阵列天线方向图的影响。

本文对16单元的开口波导组成一维线阵进行了幅度、相位赋形，阵列形式与图2所示的阵列相同，单元间距归一化波长同样为0.6λ0。为了说明阵中单元方向图的影响，本文在赋形过程中考虑了两种情况，一种是将阵中单元方向图代入优化过程而另一种没有代入。阵中单元辐射方向图数据提取的是Ansoft HFSS全波仿真数据。阵列综合中采用了文献[1]所述的方法，即连续快速傅里叶变换法(SFFT)与人工智能优化相结合的优化算法。优化完成后将赋形结果——各单元的幅度、相位输入Ansoft HFSS进行全波仿真。图4给出了三组曲线对比，分别是单元方向图加入优化过程的赋形方向图、未考虑单元方向图的赋形方向图以及给定的目标方向图。

图4可以很明显地看出单元方向图对阵列赋形结果的影响，在主瓣20°范围以内，三者曲线均符合得较好。但是，当主瓣20°范围以外，未考虑单元方向图的赋形结果与给定的目标方向图偏离较大，45°时与目标方向图值差了将近3dB。由此可见，单元方向图对阵列方向图赋形结果影响较大，对宽波束综合需要考虑单元方向图因素。本例中仅考虑了单个频点。在工程应用中若工作频带内单元方向图随频率变化剧烈，则在阵列综合中还需分别代入各频点的单元方向图进行优化。

图4 阵列赋形结果对比图

2.3 边缘效应的影响

对于大型阵列，由于阵列单元的辐射环境类似，其阵中的单元方向图基本相同。在阵列边缘的单元由于单元所处辐射环境不同，其辐射方向图、单元匹配也会出现较大的差别。图5所示的是图2阵列中各单元的E面辐射方向图，可以看出阵中单元4～13由于所处的辐射环境类似，其单元方向图几乎完全相同，而边缘单元由于辐射环境不同辐射方向图差异较大，特别是边缘单元1与单元16。工程上为了减小这些差别可以通过在阵面四周安装哑元(寄生单元)——与阵中相同的辐射单元末端接匹配负载来解决。实际应用时常由于阵面体积、重量、成本等因素的限制，无法安装哑元，此时在阵列综合中考虑阵面边缘处单元的差异以使阵面性能更加准确。

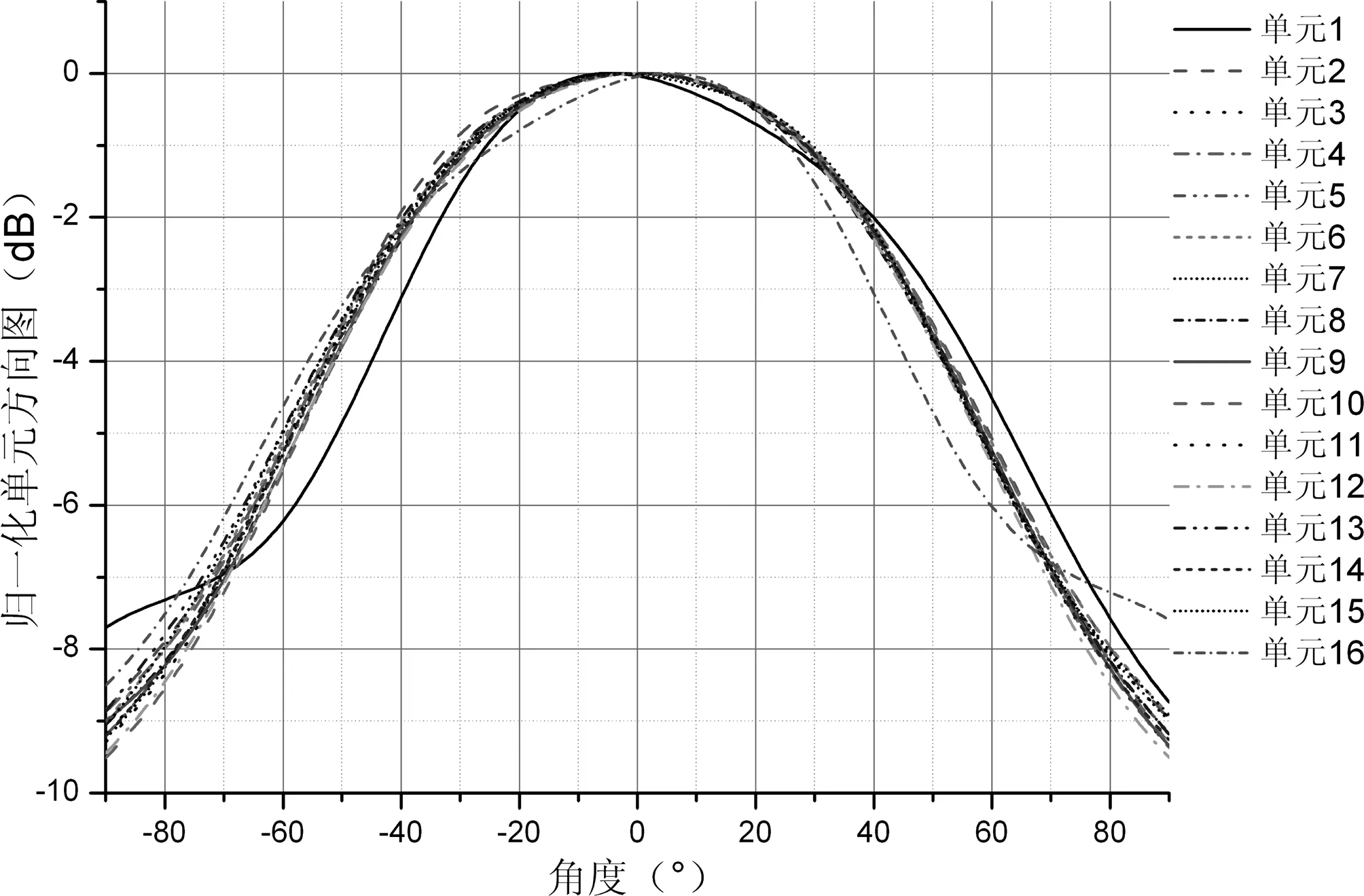
图5 阵列各单元E面方向图

本文还以16单元开口波导组成的一维线阵为例，将45°余割平方波束作为赋形目标，不同的是在这次赋形中考虑了阵列边缘单元的辐射特性差异。将优化权值代入Ansoft HFSS得到全波仿真方向图，程序优化计算得到的方向图称为理论优化方向图，赋形结果如图6所示。

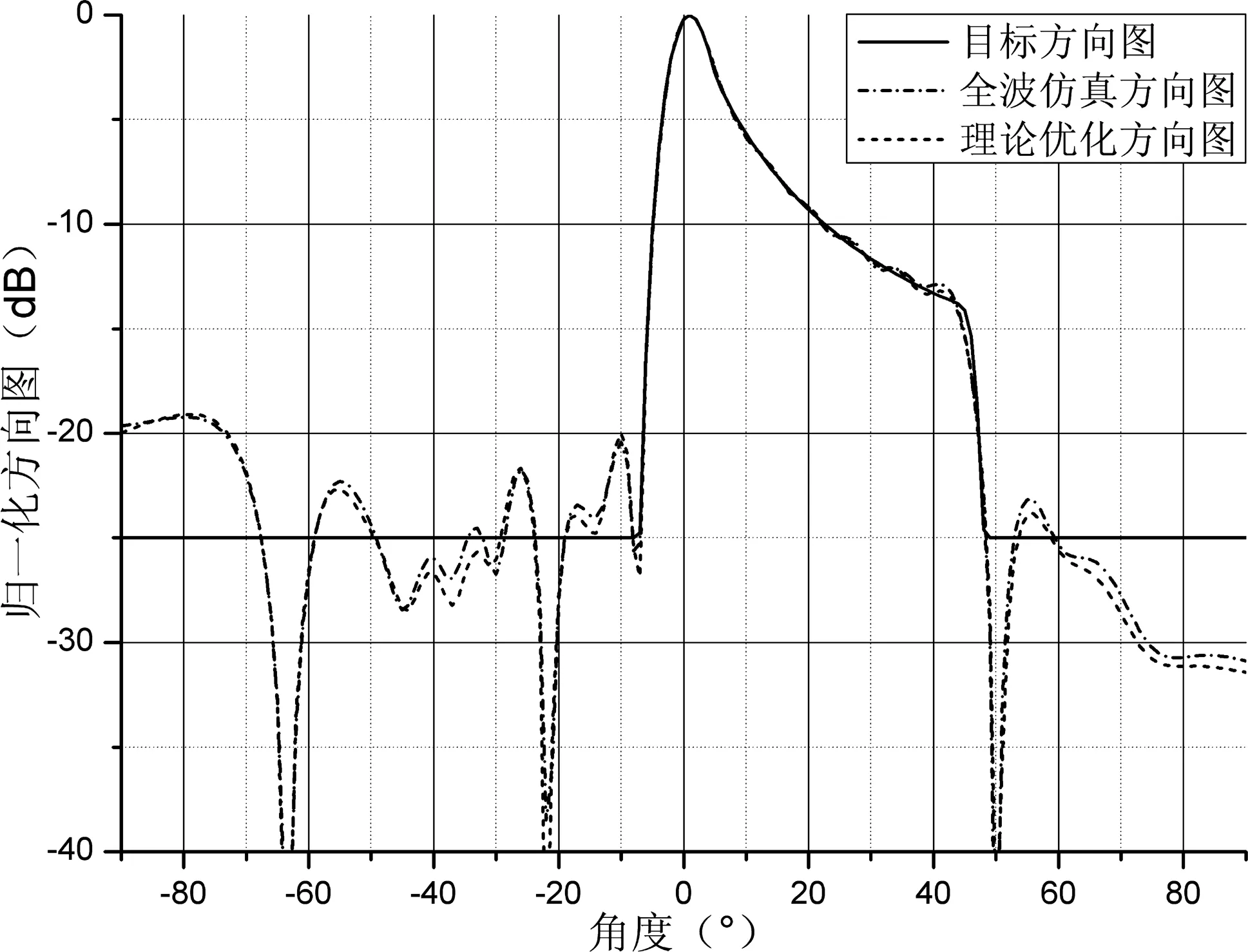
图6 理论优化方向图与全波仿真方向图对比图

从图6中可以看出，理论优化方向图与全波仿真方向图几乎完全吻合，其中旁瓣区域的微小差异是由于优化过程中未考虑阵中各单元方向图间的微小差异引起的。由于Ansoft HFSS全波仿真考虑了单元间互耦等效应，本例还间接证明了考虑单元辐射差异也就等效于考虑了阵列单元互耦等效应，这将可以更精确地模拟阵面性能。当阵列规模较大时由于边缘效应引起的误差较小，可以根据实际情况忽略该误差简化优化流程，提高优化效率。

3 结束语

传统的阵列综合通常假定辐射单元各向同性且忽略单元间互耦，在工程应用中，忽略单元方向图带来的误差会使赋形结果的可靠性大大降低。本文首先建立了阵列方向图与单元方向图关系的数学模型，在此基础上分析了单元方向图对阵列指向精度的影响，发现在小规模阵列中，单元方向图对阵列指向精度影响较大，实际应用中可以根据实测结果反求各单元相位分布来修正波束指向偏差。为了考虑单元方向图对赋形方向图的影响，本文在对45°余割平方波束赋形时，优化过程中代入了阵中单元方向图，结果表明采用该措施后赋形结果与目标方向图吻合得更好。如果单元方向图随着频率变化剧烈，则在赋形过程中还需考虑各个频点的单元方向图。最后本文以一维线阵为例考虑了阵列中边缘单元的辐射差异，结果表明在优化过程中考虑这些差异可以使计算结果更为可靠。本文中仿真代入的单元方向图依据的是电磁仿真结果，工程应用中可以通过实验测试的方法获得更为准确的单元方向图数据。

[1] Boeringer D W,Douglas H Werner.Particle Swarm Optimization Versus Genetic Algorithms for Phased Array Synthesis[J].IEEE Trans.on Antennas and Propagation,2004,52(3):771-779.

[2] 郭燕昌，钱继曾，黄富雄，冯祖伟.相控阵和频率扫描天线原理[M].北京：国防工业出版社,1978:5-12.

[3] 林昌禄，聂在平,等.天线工程手册[M].北京：电子工业出版社,2002:965-966.

[4] 谢拥军，刘莹,等. HFSS原理与工程应用[M].北京：科学出版社,2009.

Effect of cell pattern on integrated performances of arrays

CONG You-ji, LU Qin, JIAN Lin

(No.724 Research Institute of CSIC, Nanjing 211153)

When it comes to the antenna array integration, the conventional methods always assume the cell radiation pattern is isotropic and ignore the couple effect, which can lead to large errors in engineering applications. A math model of the effect of the antenna cell pattern on the performances of antenna arrays is established, and the pointing accuracy of arrays and the pattern shape are simulated, compared and analyzed. In order to minimize the errors caused by the cell pattern, the cell pattern is considered when the desired pattern is formed, and the example indicates that this method is effective. The effect of different radiation characteristics of antenna cells in array edges is also considered, and simulation results show that calculation precision can be further improved when these differences are taken into consideration.

cell pattern; array antenna; pattern integration; pattern shape

2013-12-11；

2014-01-15

丛友记(1986-)，男，工程师，硕士，研究方向：微波技术；卢青(1981-)，男，高级工程师，博士，研究方向：微波技术； 简玲(1980-)，女，工程师，硕士，研究方向：微波技术。

TN821.8

A

1009-0401(2014)01-0025-04