线性代数对学生发展影响的调查研究
2014-09-07李红刚李力沛
李红刚,李 玲,李力沛
(1.重庆邮电大学 数理学院,重庆 南岸 400065;2.长江师范学院,重庆 涪陵 408100)
1 本课题的研究现状及意义
线性代数课是社会发展和文理科各门课程的基础。线性代数的抽象思维和表述问题的方法是人们认识世界、改变生活的最基本的思想与方法之一,在提高学生逻辑思维、抽象能力方面有独到之处。但是,目前的线性代数课程教学面临如下问题[1-3]:(1)教材内容强调系统严谨,缺乏知识应用性;(2)教学课时数减少难以较好地完成基本内容和方法的教学;(3)教学中师生之间缺少互动交流;(4)学生缺乏对线性代数课程的作用、学习目的的认识。这就导致了学生学习线性代数困难、畏难、效果较差的现状,对学生素质的培养产生了不良影响。线性代数教学研究者认为当前的线性代数教材弱化了数学教育功能与价值,缺乏对现代数学思想、数学文化等的介绍与研究, 教学中忽视了提高学生对其应用价值的认识和实践;忽视了宏观把握各个专业和各门课程之间的相互影响。造成了学生知识基础不牢、问题表达不清、能力弱和发展后劲不足的状况。 因此,我们客观、定量、全面分析线性代数课对学生发展的影响程度,反应、表达学生的学习境况与诉求,发现教育中的问题,对促进线性代数课程改革和建设, 弥补线性代数对个人发展影响的相关研究中泛泛而论的不足以及为高校改革教育与人才培养规划提供参考, 改善不利学生成才的局面都具有积极的意义。
2 问卷调查法的介绍
问卷调查法就是通过用书面填表的形式间接搜集研究材料获得信息的一种调查手段。其种类可分为自填式问卷调查和代填式问卷调查两种。问卷的结构一般由卷首语(调查者的身份、单位、调查内容、填写问卷说明、其他事项)、问题(问卷主体部分,有开放式和封闭式两种),编码(利于资料数量化)和致谢语四个部分组成。问卷设计原则主要包括目的性、逻辑性、通俗性等。我们的调查以问卷星为问卷调查平台,其使用流程为:在线设计问卷→发布问卷并设置属性→发送问卷→查看调查结果→创建自定义报表。在问卷设计中,做到突显调研目的,确定调查方法、确定各问题内容,搜集数据资料。根据本文研究课题,从受调查者的主观兴趣和客观影响两个方面来综合评判线性代数对学生发展的影响。问卷共设有19个问题,分三个模块:模块一显示受调查人的基本身份信息,保证数据资料的准确率;模块二显示调查人对线性代数课程的主观兴趣度;模块三显示线性代数课程对受调查人的客观影响程度。线性代数课是否对学生的个人发展有影响,主要表现在对其他课程的学习、对解决实际问题、对毕业后的就业是否起到积极的作用。
3 线性代数课对学生个人发展影响的层次模糊综合评价[4]
层次模糊综合评判法是一种对多因素多层次制约的事物或对象,运用模糊数学理论的隶属度把定性评价转化为定量评价的分析方法。其评价结果清晰, 系统性强, 能较好地解决模糊的、难以量化的非确定性问题[4]。在本文中,我们针对全国2000多份问卷采集的数据,应用层次模糊综合评判模型作出线性代数课程对学生发展影响的分析研究。其实际处理过程如下。
3.1 建立层次结构模型
我们将问卷分为三个指标层,其中准则层的一级指标2个,二级指标7个,三级指标2个,将因素集分为3 组,U={u1,u2}为第一级因数集;U1={u11,u12,u13,u14},U2={u21,u22,u23}为第二级因素集;U14={u141,u142},为第三级因素集(如图3.1所示)。

图3.1 指标体系和层次结构
设置评语集 由于每个指标的评价值不同,就会形成不同的评价等级。线性代数对各因素指标的评价分为影响大、影响较大、影响一般、影响较小、没影响等五个级,并构成了评语集V={v1,v2,v3,v4,v5}。
判断矩阵构造 设线性代数课对个人发展影响的综合评价准则为:主观兴趣和客观影响,且客观影响的作用大于主观兴趣。所以,其准则层对目标层的判断矩阵为:
设主观兴趣的综合评价准则为:喜欢度、重视度、难易度、精力量,两两比较,得指标1层对准则层的判断矩阵:
设精力量的综合评价准则为:实际所花精力量和期望所花精力量,且实际所花精力量的作用明显比期望所花精力量的作用更大。所以,指标2层对指标1层的判断矩阵:
设客观影响的综合评价准则为:对其他课程的帮助、对解决问题的帮助、对求职就业的帮助,两两比较,得指标1层对准则层的判断矩阵:
判断矩阵相关数据的计算 分别计算判断矩阵B,B1,B14,B2的权重向量,最大特征值,一致性指标,随机一致性指标于表3.1:
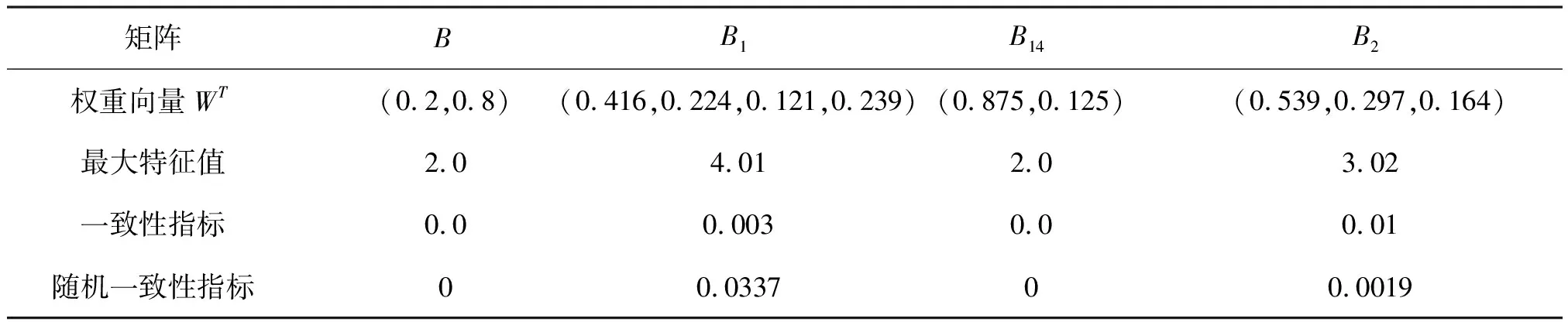
表3.1 各判别矩阵的权重向量、最大特征值、一致性指标、随机一致性指标
由表3.1得出每个判别矩阵的随机一致性指标的值均小于0.1,因此,它们都通过一致性检验。
层次模糊综合评判 评语集分别对应了问卷的答案选项,将问卷数据换算成百分比,以小数形式带入,如表3.2所示。
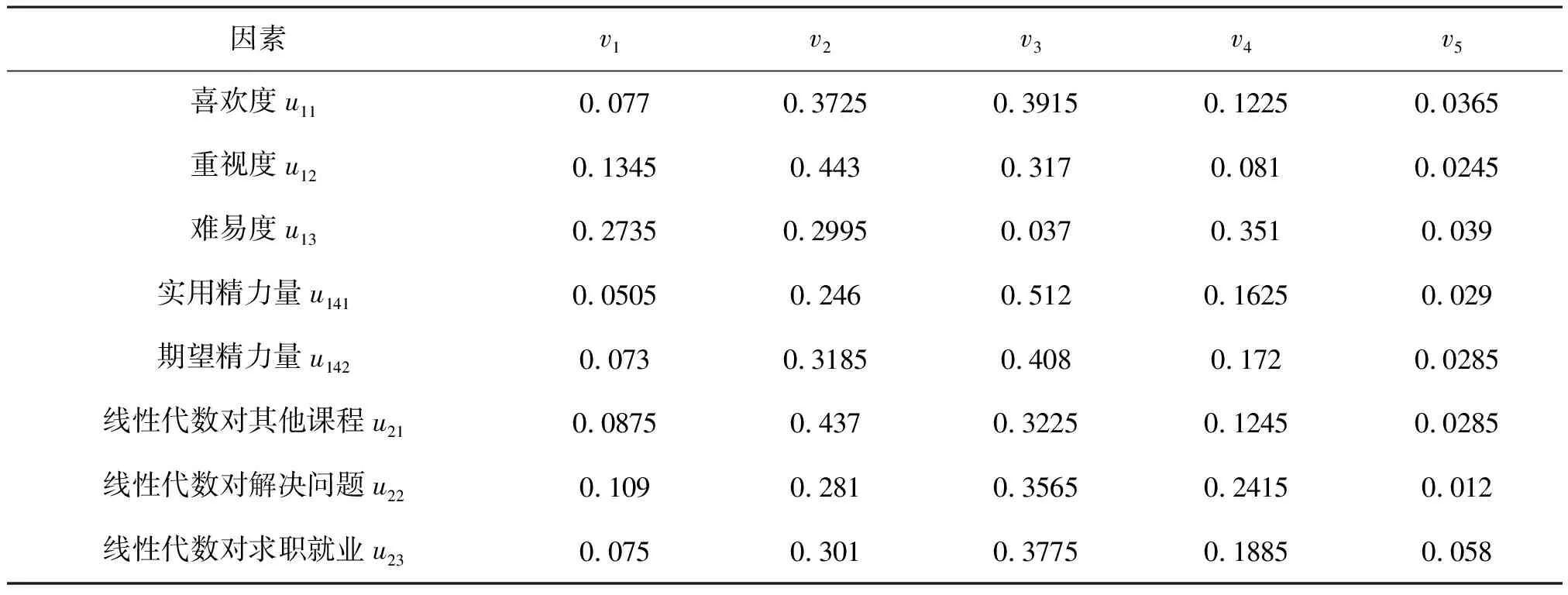
表3.2 对应因素的评语集数据
通过上表,可以得到对喜欢度u11,重视度u12,难易度u13的评判矩阵:
实际精力量u141,期望精力量u142的评判矩阵:
线性代数对其他课程的影响,对解决问题的影响和对求职就业的影响的评判矩阵:


表3.3 线性代数层次模糊综合评判表
4 线性代数对学生个人发展影响的结论与建议
在表3.2中,H14,H1,H2与H分别表示学生学习线性代数课的期望及实用精力量、学习线性代数课的主观兴趣、学习线性代数课后在三个方面对个人发展的客观影响以及学生学习线性代数课程的综合影响。根据最大隶属度原则,我们获得的结论如下:
(1)三级指标H14所花精力与二级综合指标H1主观兴趣的评价等级均为“影响一般”,说明了学生在学习线性代数时所花精力量和其学习兴趣只是一般。
(2)二级指标H2客观影响和一级指标H综合影响的评价等级都为“影响较大”, 说明线性代数课对学生其他课程学习、解决实际问题能力、个人求职工作以及综合性的全面影响较大。
由此结论看出:线性代数作为必修课对学生个人发展的客观影响和全面性的综合影响都大,因此,学好线性代数完全必要。然而,学生学习线性代数的主观努力还不够,大有潜力可挖掘。
造成这种情况的原因不少。我们通过调查发现,这主要表现在大学线性代数教育与中学初等数学教育的较大差别上。大学一年级的学生,多年受应试教育的影响,习惯形象具体的思维和被动学习的教学模式,而对线性代数的语言叙述、逻辑思维、抽象表达和教师教学方法等不适应。这就直接导致学生认为线性代数课难学,兴趣降低,积极性受挫,学习效果变差,并进入不良循环状态。
对于这种现状,建议教师在学习方法、逻辑思维、抽象表达等方面多给学生予指导和帮助,使他们平稳过渡到大学学习环境中来;建议教材改革中注重应用、人文、理论知识的结合,以提高学生学习兴趣和积极性;建议考试灵活多样,促进学生自主学习,以提高学生的能力。
尽管线性代数课的教育教学存在一些问题,但它对学生一生的发展影响是深刻的。我们曾在人文意境中讨论数学的教育教学问题时指出[5-6]:“数学(包括是线性代数)是人类认识、利用和改变客观世界的有力工具,是人文世界的一个部分。其发展过程和历史现状充满了辩证唯物主义的思想方法。作为教师应激发学生的学习兴趣,引导其掌握数学的分析方法。”作为学生学好线性代数知识,有助于提高自己的学习能力。而我们要做的则是进一步增强其影响,培养更多的高素质人才以满足社会的发展需要。
参考文献:
[1]陈怀琛. 论工科线性代数的现代化与大众化[J].高等数学研究,2012,15(2).
[2]陈怀琛,高淑萍,杨威.科学计算能力的培养与线性代数改革[J].高等数学研究,2009,5(52).
[3]徐海静,何立官.矩阵思想在《线性代数》教学中的应用[J].西南师范大学学报(自然科学版),2013,37(5).
[4]汪培庄,韩立岩.应用模糊数学[M].北京:北京经济学院出版社,1989.
[5]李红刚,张杰,曾令淮.数学方法教育中的人文意境(I)—数学教师需要知道[J].喀什师范学院学报,2006,27(6).
[6]李红刚,杨娟.数学方法教育中的人文意境(II)—教师能做到[J].喀什师范学院学报,2007,31(6).
