铰接多浮体系统在规则波作用下的运动响应
2014-09-07王桂波,勾莹,滕斌,曹光磊
王 桂 波, 勾 莹, 滕 斌, 曹 光 磊
( 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024 )
铰接多浮体系统在规则波作用下的运动响应
王 桂 波, 勾 莹*, 滕 斌, 曹 光 磊
( 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024 )
基于线性势流理论,利用模态法在频域内研究了铰接多浮体结构在规则波作用下的运动响应.首先采用边界元法建立边界积分方程求解水动力系数及波浪激振力,然后基于最小势能原理采用拉格朗日乘子法推导出系统的约束矩阵,并利用该约束矩阵建立系统运动方程求解各运动模态的运动响应幅值.通过与已发表的5个铰接漂浮方箱在规则波作用下运动响应结果的对比,证明了方法的正确性和有效性.以3个铰接的箱型浮体为例,讨论了水深、铰接位置对结构运动响应的影响.研究发现水深、铰接位置均会对结构的运动响应产生一定影响,且对于不同的波浪周期其影响程度也不同.
高阶边界元法;铰连接;多浮体;运动响应
0 引 言
近年来,随着海洋资源的进一步开发,多浮体结构的应用也越来越广泛,例如LNG运输船的装卸载操作、海蛇波浪发电装置、海上漂浮机场、移动海上基地等.
相对单个浮体,多浮体系统中每个浮体在波浪中的运动特性是不同的,因此既要考虑每个浮体与流场间的耦合作用,还要考虑多体系统内各物体间水动力耦合影响.谢楠等[1]利用三维源汇分布法计算了浮体间距对浮体运动响应的影响,结果表明,相互间水动力耦合作用显著.Choi等[2]利用高阶边界元法计算了两条船旁靠和串靠时的运动响应;Gou等[3]利用快速多极子方法计算了3个浮体船在规则波作用下的运动响应,并与单个船体的运动响应进行对比,发现由于船体间水动力的影响波浪激振力和水动力系数均发生了显著变化.以上这些研究结果都说明必须完整地考虑浮体间的水动力耦合影响.
对于浮体间有连接的情况,还需要考虑连接力对各浮体运动响应的影响.海上浮桥、海上漂浮机场都可以简化为由刚性铰相连接的多浮体结构.对于采用刚性铰相连接的多浮体系统,由于其连接会限制浮体间的某些相对作用模态,在进行水动力分析时可采用直接模态分析法.直接模态分析法即根据浮体间的连接方式分析系统可能的运动模态,根据分析得到的运动模态求解相应的辐射势并建立相应的运动响应方程,浮体间的连接作用力作为系统间的内力,从而求出系统的运动响应.Newman[4]和Lee等[5]采用这一方法研究了波浪与铰接和固接多浮体相互作用的问题,在Lee等[5]的文章中还考虑了浮体的弹性刚度对多浮体系统运动响应的影响;Diamantoulaki等[6]采用直接模态法研究了入射波频率及浮体个数对铰接多浮体系统运动响应的影响.虽然直接模态法针对特定的铰连接方式确定系统的运动模态,减少了计算量和存储量,但对于一些复杂结构,在计算之前不易准确分析出系统的运动模态,对于采用非铰连接形式的多浮体系统,这一方法也失去了其可减少计算量的优势.由于每个浮体可分解为6个自由度,更普遍的总模态法认为系统的总模态数为6×N(N为物体的数量),对每个浮体列运动响应方程,浮体间的连接作用力作为外力,根据浮体间连接处的力和位移特性补充方程,得出以6×N个响应幅值及浮体间连接力为未知量的方程组,通过求解得出系统的运动响应和连接作用力.Hong等[7]利用总模态法研究了两并排船只在波浪作用下的运动响应并与实验结果进行对比;Kim等[8]采用总模态法研究了浮体形状以及连接刚度对系统运动响应的影响;勾莹等[9]利用总模态法研究了波浪与两个铰接和柔性连接方箱的相互作用问题,发现当入射波频率与箱体的自振频率接近时箱体的运动响应会发生快速变化;Tajali等[10]利用总模态法研究了吃水深度、系泊的有无,以及波浪入射方向对铰接多浮体系统运动响应的影响.总模态法中根据浮体间连接处的力和位移特性补充方程时一些学者也利用不同的方法进行实现,勾莹等[9]根据两漂浮方箱连接点处的位移匹配条件直接补充运动约束方程求得各浮体的运动响应;沈庆等[11]利用虚功率原理导出多体系统凯恩方程求解各浮体的运动响应;Sun等[12-13]利用拉格朗日乘子法引入约束矩阵,联合各浮体的运动方程导出系统的整体运动方程,与前两种方法相比,当浮体的个数较多,且浮体间的连接方式比较复杂时引入约束矩阵表达形式更为简洁,也更适合计算机编程计算.
本文利用总模态法对多浮体系统进行水动力分析,通过引入约束矩阵建立多浮体系统的运动方程,研究水深、铰接位置及结构布置方式对铰接多浮体系统运动响应的影响.
1 边界积分方程的建立及速度势求解
假定波浪中有N个作小幅简谐振荡的浮体A,B,C,…,浮体间为刚性铰连接,如图1所示,整体坐标系OXYZ为固定坐标系,坐标系O1X1Y1Z1,O2X2Y2Z2,O3X3Y3Z3,…为局部坐标系,所有坐标系原点均位于静水面上.
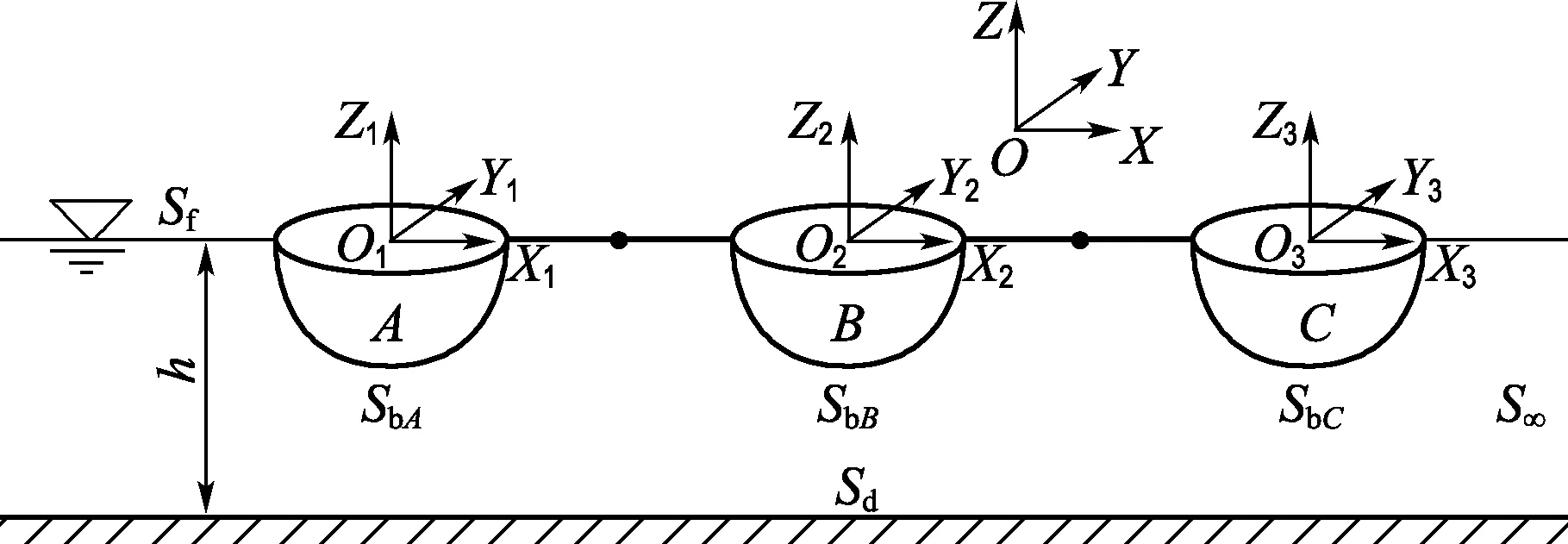
图1 坐标系定义
在流域内,函数u和v在边界上具有一阶和二阶导数,且满足第二格林公式:
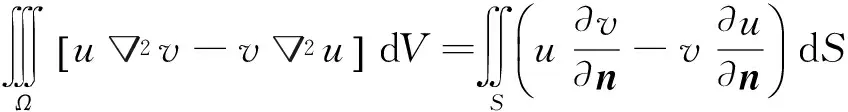
(1)
式中:Ω为流域;n为物面的单位法向量,指出流体流向为正;S=Sb+Sf+Sd+S∞,为流域边界,Sb为物面,且Sb=SbA+SbB+SbC,…,Sf、Sd、S∞分别为自由水面、水底面、无穷远处水面.令φ=u为速度势函数,G=v为源点在(X0,Y0,Z0)的格林函数.针对不同问题和边界条件,采用不同形式的格林函数,本文采用满足除物面条件以外所有边界条件的格林函数,使积分区域仅限于物体表面Sb上,即格林函数G满足以下控制方程和边界条件:

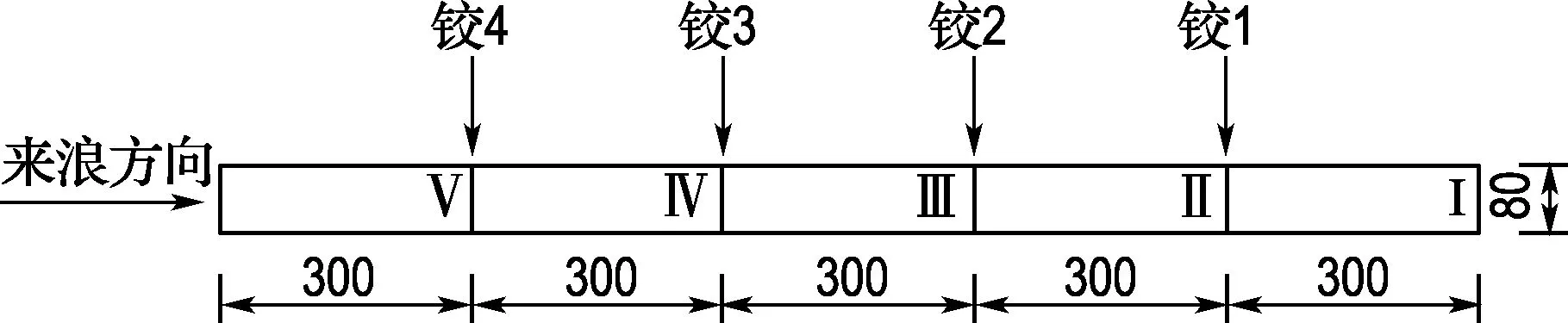
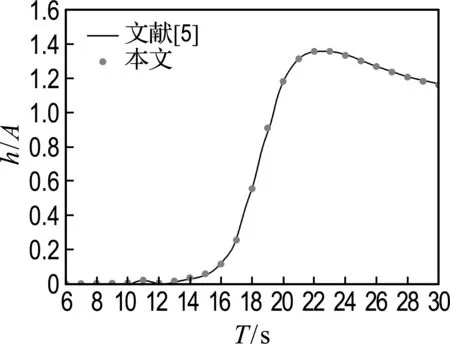
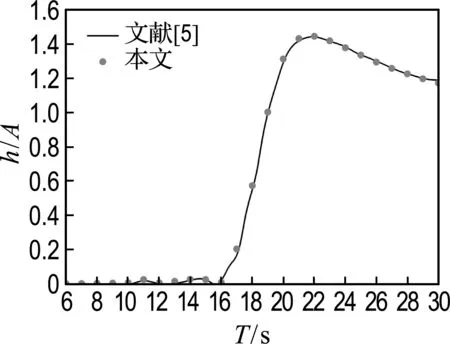
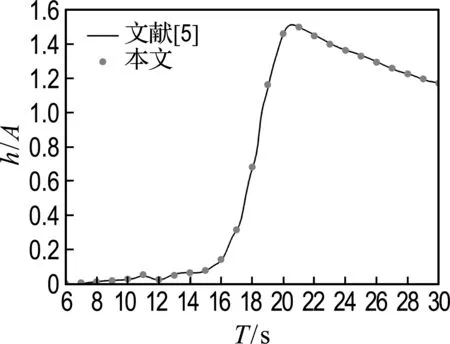
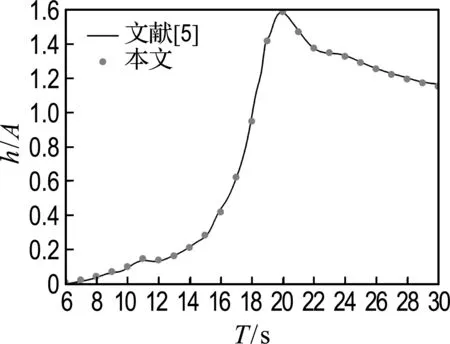
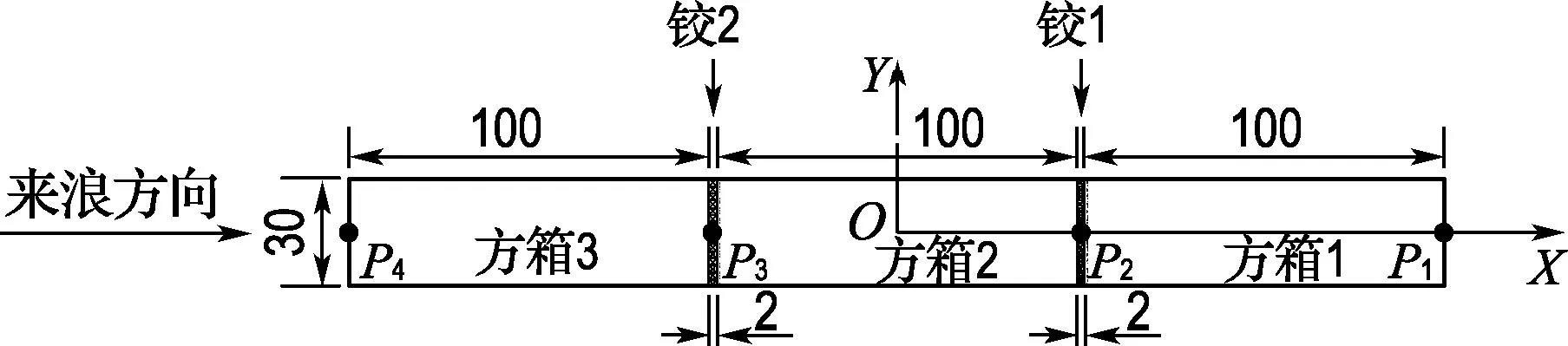
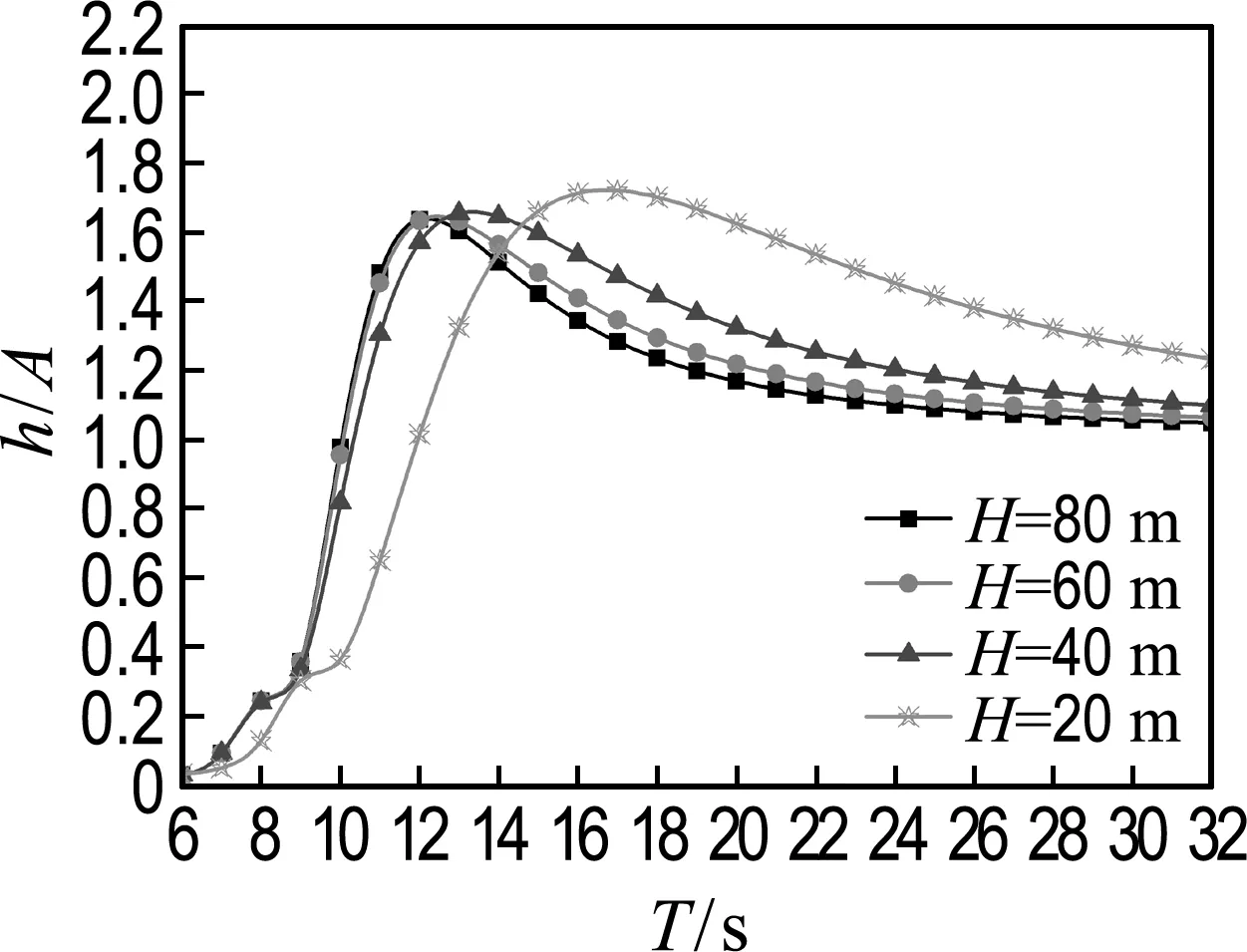
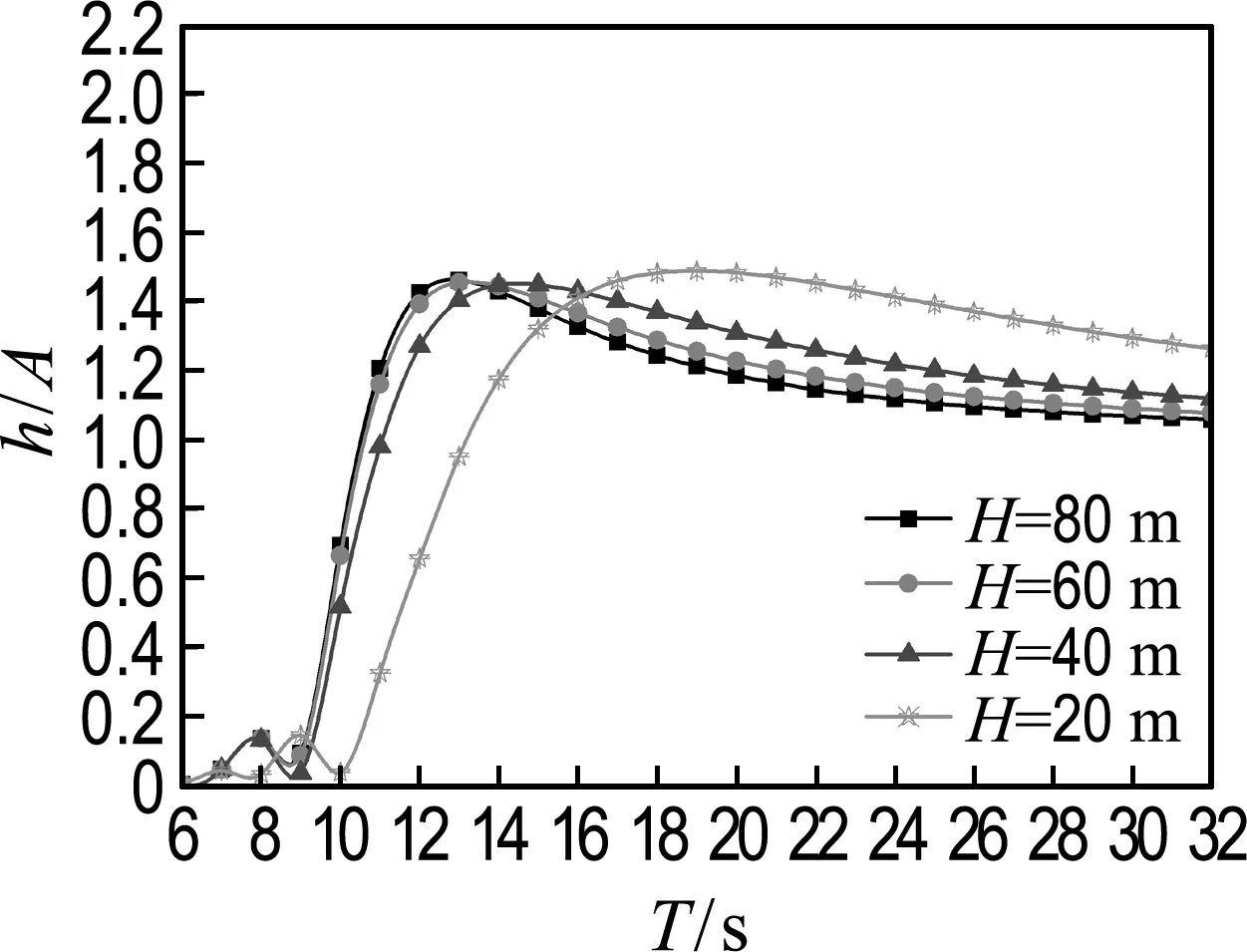
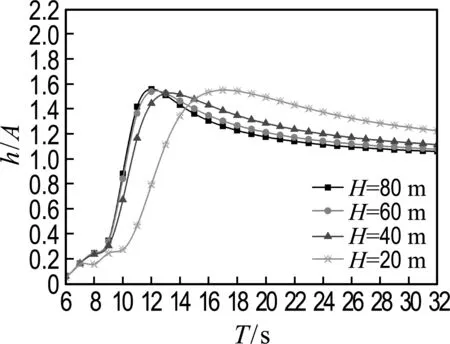
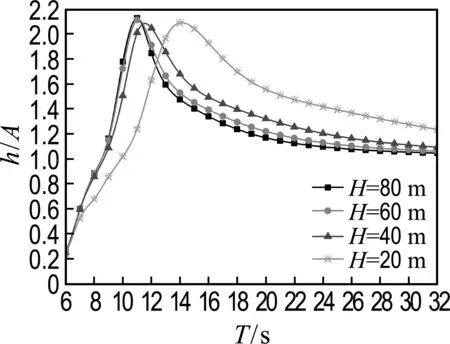
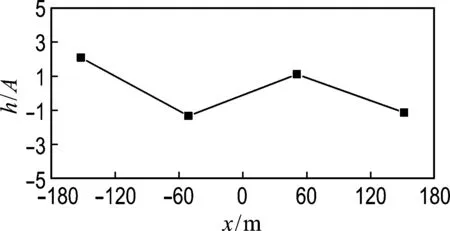
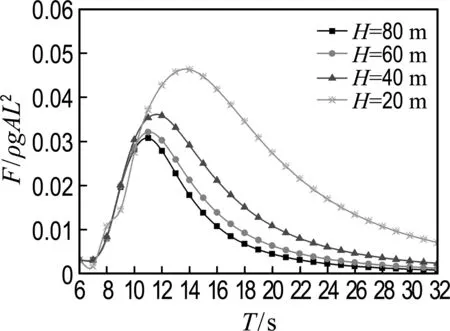
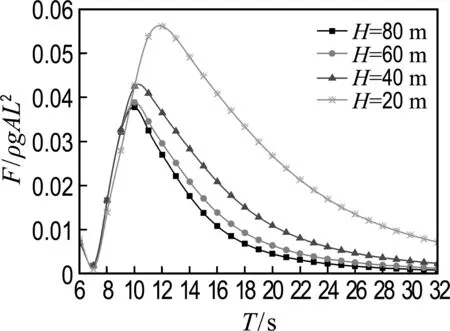
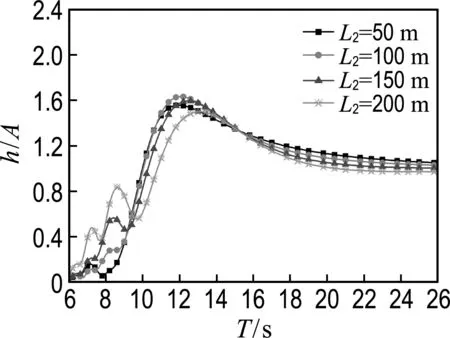
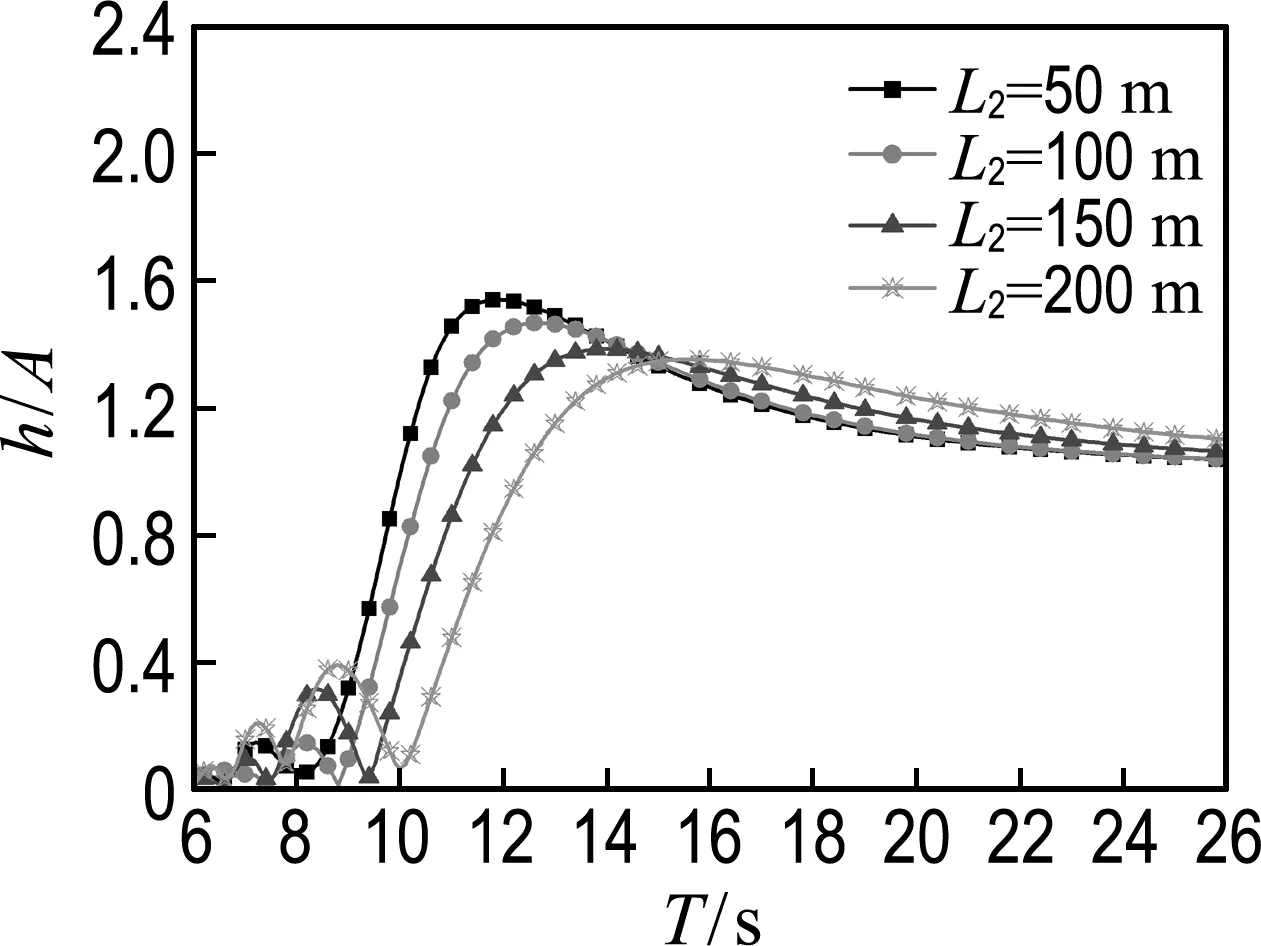
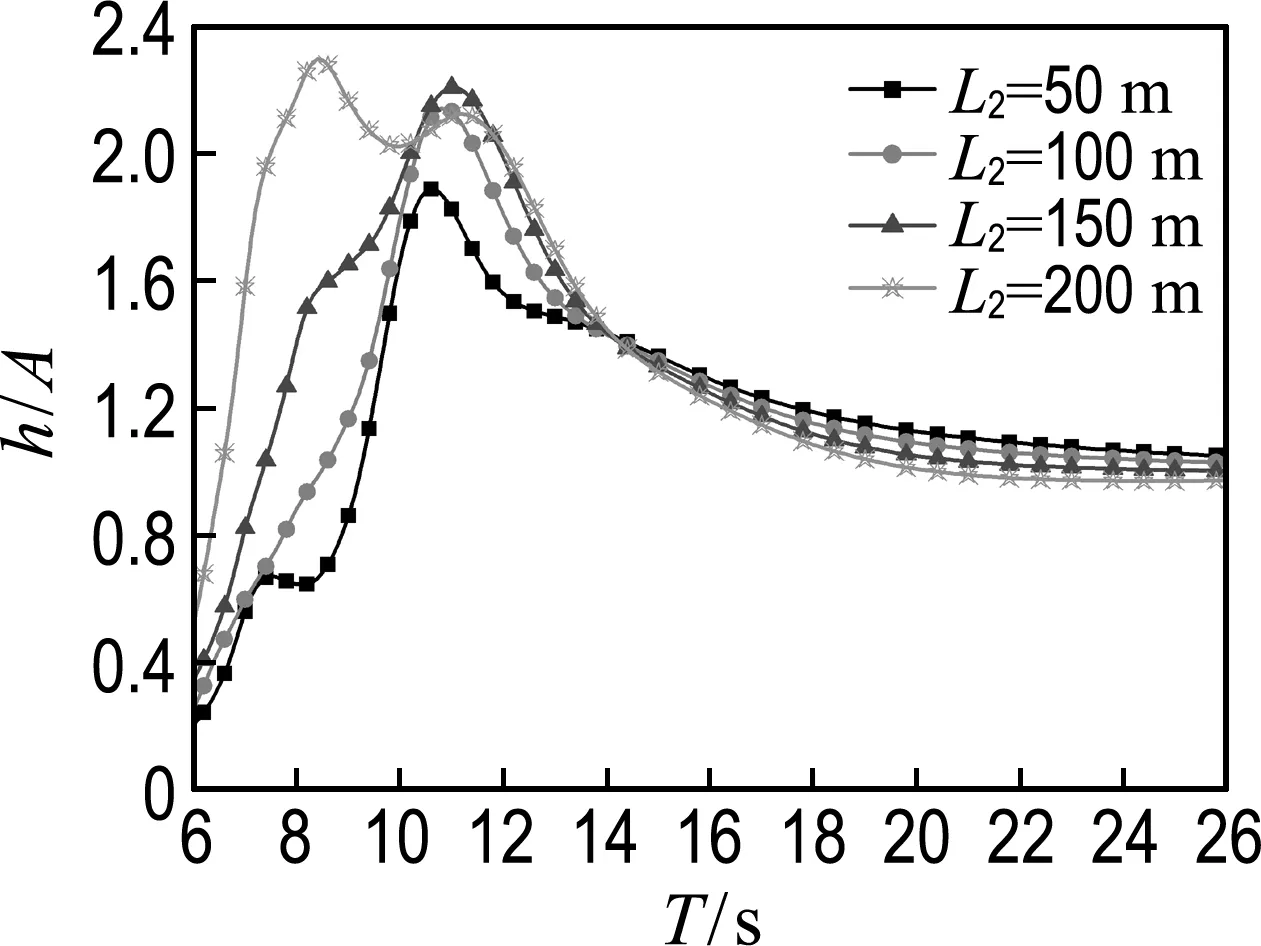
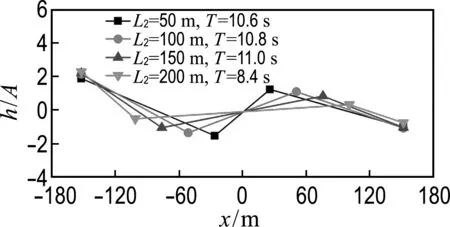
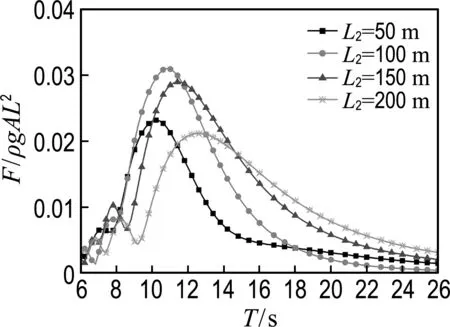
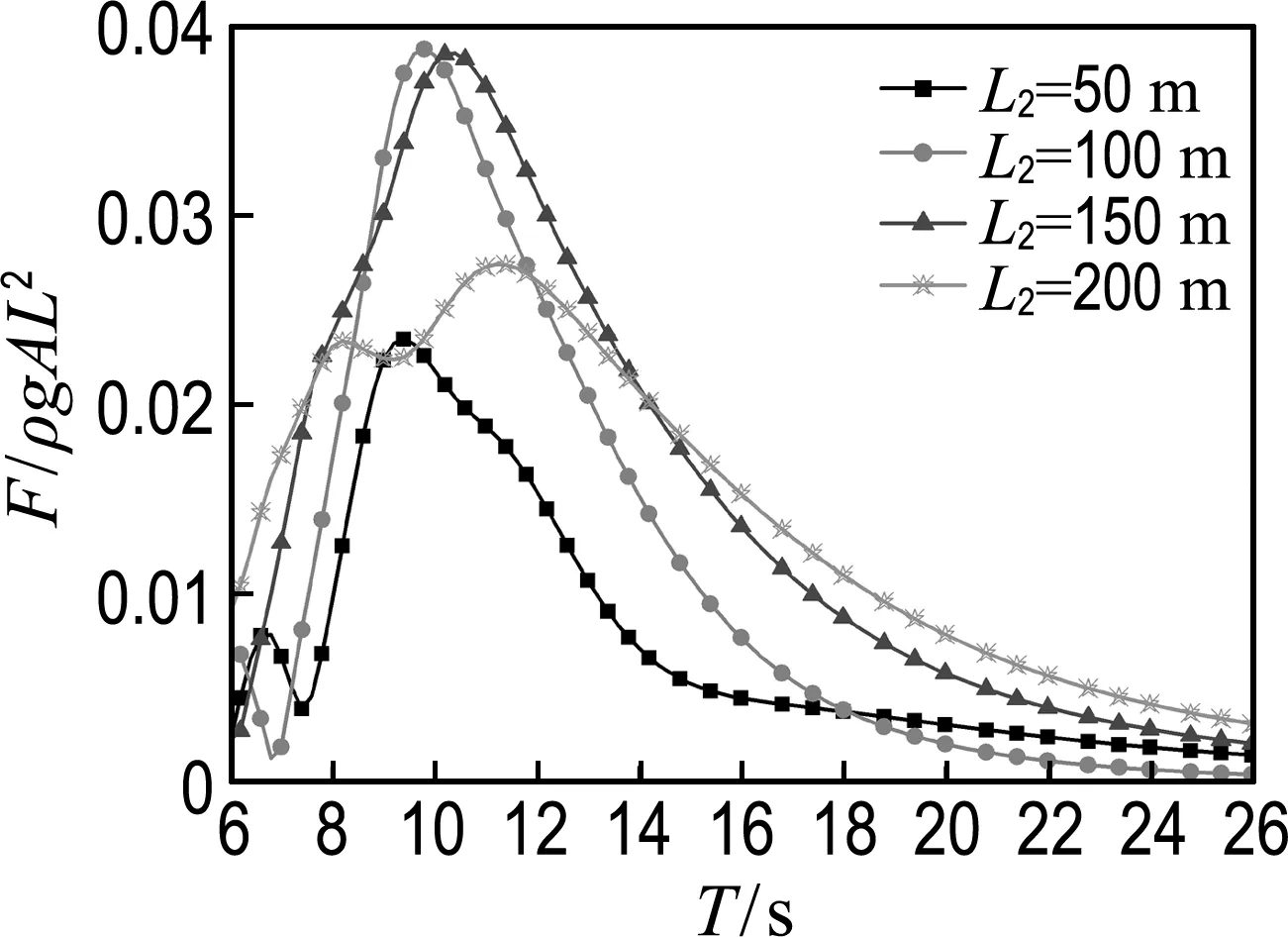
-h Gz=0;z=-h Gr=0;r→∞ (2) John[14]于1950年导得了满足上面条件的格林函数G: (3) 式中:r=[(x-x0)2+(y-y0)2+(z-z0)2]1/2;r1=[(x-x0)2+(y-y0)2+(z+z0+2h)2]1/2;ν=ω2/g,为深水中的波数.将速度势φ和上述格林函数应用第二格林公式(1)可得积分方程 (4) 其中α为固角系数,其取值分别为 (5) 式中:Θ为物体表面所占的空间角度. 流场中速度势可以表达为如下形式: (6) 当波浪的入射角与x轴的夹角为β时,流场中的入射势φi可以写为 (7) 式中:A为入射波的波幅;g为重力加速度;k为波数,且波浪频率与波数之间的关系满足色散方程ω2=gktanhkh;φd为绕射势;φj(j=6(I-1)+1,…,6(I-1)+6)(其中1≤I≤N)表示浮体I作单位幅值运动,其他浮体不动时产生的辐射势;εj(j=6(I-1)+1,…,6(I-1)+6)(其中1≤I≤N)表示浮体I的运动幅值.综合式(4)和式(6)可以求出绕射势和辐射势,进而求出附加质量、辐射阻尼,以及波浪激振力. 对于简谐波与结构物相互作用问题,浮体的运动响应也应是同频率下的简谐运动,因此将浮体的运动响应分离出时间因子,得到复值形式的运动响应ε.根据线性势流理论,考虑浮体间水动力耦合的影响,利用总模态法,在频域内建立系统的运动响应方程,对于有连接的多浮体系统,各浮体的运动方程表达形式为 (8) 式中:n为浮体的数量,M、a、b、C、fex、fl分别为浮体的质量矩阵、附加质量阵、辐射阻尼阵、恢复力矩阵、波浪激振力矩阵、浮体间的连接所产生的作用力和力矩,下标II表示由于浮体I运动在浮体I自身上引起的物理量,下标IJ表示由于浮体J运动在浮体I上引起的物理量,为表达方便将式(8)简化为如下形式: Kε=F (9) 式中:K、ε、F分别为刚度阵、物体位移向量、系统所受外力向量,所以系统内势能的大小可以表示为 (10) 对于有连接的多浮体系统,在连接点处应满足位移连续条件,即Dε=0,所以应用拉格朗日乘子法有 (11) 令m表示系统中所有约束连接点处约束个数的总和,则F、ε、K、D、λ的大小分别为6n×1、6n×1、6n×6n、m×6n、m×1.对方程(11)两边同时变分得到 Kε+DTλ=F Dε=0 (12) 将方程(12)进行整理得到 (13) 该方程即为系统的运动方程.以两个铰接浮体结构I、J为例对建立约束矩阵D的过程进行说明,当结构仅可以绕y轴转动时,在铰接点处满足位移连续条件: ξI1=ξJ1,ξI2=ξJ2,ξI3=ξJ3,ξI4=ξJ4,ξI6=ξJ6 (14) 式中:ξI和ξJ分别表示浮体I和浮体J在铰接点处的平动位移和转角.其中 ξI1=εI1+Z0×εI5-Y0×εI6 (15) ξJ1=εJ1+Z0×εJ5-Y0×εJ6 (16) 式中:(X0,Y0,Z0)是铰接点处的坐标,εI1,…,εI6为浮体I的平动位移和转角,εJ1,…,εJ6为浮体J的平动位移和转角,且上述计算均相对于整体坐标系.同理可以得到ξI2、ξI3、ξI4、ξI6和ξJ2、ξJ3、ξJ4、ξJ6的表达式,将这些表达式代入式(14)中,得到约束矩阵D的表达式为 (17) 3.1 数值验证 采用与文献[5]相同的数值模型,模型结构如图2所示,其中方箱各处密度均匀,每个方箱的长、宽、高、吃水深度分别为300、80、12、6 m,水的密度取1 025 kg/m3,在每个方箱表面长、宽、高方向分别划分30、8、2个单元,总的单元数为1 832,总的节点数为5 913.利用上文中的方法建立5个铰接方箱的约束矩阵,计算了当水深为无限水深,来浪方向为0°时该铰接系统的运动响应,并与文献[5]的计算结果进行对比,其中波浪入射角为来浪方向与x轴正向的夹角. 图3为0°方向来浪时,各铰接点处的升沉位移,从图中可以看出本文的计算结果与文献[5]的计算结果吻合较好,表明程序是正确的. 图2 五方箱铰接俯视图(单位:m) (a) 铰1 (b) 铰2 (c) 铰3 (d) 铰4 图3 铰的升沉位移 Fig.3 Heave responses of hinges 3.2 水深对系统运动响应的影响 取3个方箱组成的铰接系统,系统结构如图4所示,每个方箱均为均质方箱,方箱的长、宽、高、吃水深度分别为100、30、10、5 m,方箱间的间隔为2 m,水的密度取1 025 kg/m3,波浪入射角为来浪方向与x轴正向的夹角.在每个方箱表面划分40×10×2个单元,总的单元数为1 800,总的节点数为5 703,本文计算了来浪方向为0°,水深分别为80、60、40、20 m时结构的运动响应(坐标原点定在方箱2中心,P1、P2、P3、P4点的坐标分别为P1(152,0,0),P2(51,0,0),P3(-51,0,0),P4(-152,0,0)). 图4 三方箱铰接俯视图(单位:m) 图5为P1、P2、P3、P4垂向运动响应随周期的变化情况,从图中可以看出随着水深的增加,在一定的周期范围内,P1、P2、P3、P4的垂向运动响应逐渐增大,且垂向位移峰值所对应的周期逐渐减小,当周期较大时P1、P2、P3、P4的垂向位移随着水深的增大而逐渐减小,最终趋近于一个定值.从4个点的垂向运动响应比较中可以看出当水深H=80、60、40 m时P1、P2、P3、P4的垂向运动响应变化不大;但当H=20 m时其垂向运动响应变化较大,说明水深对浮体的运动响应有一定影响,且随着水深的变化浮体的运动响应呈非线性变化.当水深较深时浮体的运动响应接近于深水情况,浮体的运动响应变化不大;当水深较浅时浮体的运动响应受水深的影响变化比较明显.同时从图中还可以看出迎浪侧的P4点垂向运动响应最大,其次为背浪侧的P1点,中间两点最小.图6为水深20 m时,P4点运动响应达到最大时结构整体的位形图,从图中可看出此时各浮体结构间的相对运动情况.图7分别为铰1、2的垂向剪切力随周期的变化情况,该力除以ρgAL2进行量纲一化,其中ρ、g、A、L分别代表流体的密度、重力加速度、波幅、方箱长度,从图中可以看出当周期小于10 s时,水深对铰接点垂向剪切力的影响不大,说明此时水深对结构的相对运动响应影响较小,可视为深水情况.但当周期逐渐增大对应的入射波浪波长增长时,水深的变化对垂向剪切力有明显的影响.水深越小,在同一周期时垂向剪切力越大,说明结构间的相对运动越大.并且水深越小,垂向剪切力峰值越大,其对应的周期也越大. (a) P1点 (b)P2点 (c)P3点 (d)P4点 图5 不同水深下各铰接点的升沉位移 Fig.5 Heave responses of hinge points under different water depths 图6 H=20 m,T=14 s时结构整体位形图 (a) 铰1 (b) 铰2 图7 铰的垂向剪切力 Fig.7 Vertical shear forces acting on hinges 3.3 铰接点位置对系统运动响应的影响 为了便于研究参数影响规律,取3个方箱组成的铰接系统开展研究.每个方箱均为均质方箱,方箱的宽、高、吃水深度以及布置方式与图4相同,方箱间的间隔为2 m,方箱的总长度为定值,即2L1+L2=300 m,其中L1为方箱1、3的长度,L2为方箱2的长度.计算了无限水深条件下,来浪方向为0°时,L2分别为50、100、150、200 m时结构的运动响应(P1、P2、P3、P4点的坐标分别为P1(152,0,0),P2(L2/2+1,0,0),P3(-L2/2-1,0,0),P4(-152,0,0)). 图8分别为P1、P2、P3、P4垂向运动响应随周期的变化情况,从图中可以看出随着方箱2长度的增加,在结构垂向运动响应峰值对应的周期附近P1、P2、P3的垂向运动响应逐渐减小,但P4则相反,其垂向运动响应逐渐增大.在短周期时,各点的运动响应结果都波动较大,当周期约大于14 s时结构的运动逐渐趋于平稳,此时铰接点位置对结构的运动响应影响不大,这是因为当T=14 s时,波长约为306 m,近似于结构的特征长度,因此在周期大于14 s以后铰接位置对结构整体的运动响应影响不大.根据图8的结果可知,当L2分别为50、100、150和200 m时,P4点峰值对应的周期分别约为10.6、10.8、11.0和8.4 s,即当L2分别为50、100、150 m时,P4点峰值所对应的周期随着L2的增加而增加,但当L2=200 m时,P4点峰值对应的周期减小到8.4 s.其原因在于当L2为100 m时,结构各段的长度相同,P4点的运动响应只出现一个峰值,当L2为50、150和200 m时,结构中L1=L3≠L2,此时P4点的运动响应出现两个明显的变化过程,但当L2为50、150 m时,L1、L3对前一个变化过程影响不明显,当L2等于200 m时,L1、L3对前一个变化过程的影响比较明显,在此处出现峰值.在图9中给出了这4个周期时结构的整体位形图.从图中可以看出当L2=200 m时结构各浮体相对运动较小,比较平稳.图10为铰1、2在不同铰接位置时的垂向剪切力随周期的变化情况,将该垂向剪切力除以ρgAL2进行量纲一化,其中L取为100 m.对图10(b)中铰2的结果进行仔细分析,可以看出虽然在计算周期范围的左右两侧,即短周期和长周期部分,L2=200 m时的剪切力较大,但是在垂向剪切力出现较大峰值时,L2=200 m情况的剪切力峰值显著降低;L2=100 m即3个方箱结构特征尺度一样时其垂向剪切力最大;在大多数周期情况下L2=50 m情况的剪切力较小. (a) P1点 (b)P2点 (c)P3点 (d)P4点 图8 不同L2下各铰接点升沉位移 Fig.8 Heave responses of hinge points under differentL2 图9 结构整体位形图 (a) 铰1 (b) 铰2 图10 不同L2下铰的垂向剪切力 Fig.10 Vertical shear forces acting on hinges under differentL2 (1)采用总模态法可以使多浮体系统的水动力分析问题得到很好的解决,同时通过引入约束矩阵D使系统的运动方程有了统一写法,其表达形式更为简洁,也更适合统一编程计算求解. (2)将不同水深情况下系统的运动响应进行对比可以得到,随着水深的增大,周期较小时结构的垂向运动响应逐渐增大,对于周期较大的情况则相反,结构的垂向位移随着水深的增大而逐渐减小,最终趋于定值;当周期较小时,水深对铰接点的垂向剪切力影响不大,但当周期逐渐增大时,水深越小垂向剪切力峰值对应的周期越大,并且水深越小同一周期时的垂向剪切力也越大. (3)通过不同铰接位置情况下系统的运动响应对比可知,当结构总长度一定时,在一定的周期范围内,随着中间结构长度的增加,在结构垂向运动响应峰值对应的周期附近背浪侧结构的垂向运动响应逐渐减小,迎浪侧结构的垂向运动响应逐渐增大,当波长大于结构的特征长度时结构的运动逐渐趋于平稳,此时铰接点位置对结构的运动响应影响不大;同时还可以得出当中间结构长度较大时各浮体间的相对运动较小,此时结构比较平稳.可根据实际工程需要设计各结构的特征长度. [1] 谢 楠,郜焕秋. 波浪中两个浮体水动力相互作用的数值计算[J]. 船舶力学, 1999,3(2):7-15. XIE Nan, GAO Huan-qiu. Numerical calculation of hydrodynamic interaction of two bodies floating in waves [J].JournalofShipMechanics, 1999,3(2):7-15. (in Chinese) [2] Choi Y R, Hong S Y. An analysis of hydrodynamic interaction of floating multi-body using higher-order boundary element method [C] //Proceedingsofthe12thInternationalOffshoreandPolarEngineeringConference. Kitakyushu:The International Society of Offshore and Polar Engineers, 2002:303-308. [3] GOU Ying, TENG Bin. Research on hydrodynamics interaction between multiple floating bodies [C] //Proceedingsofthe8thInternationalConferenceonHydrodynamics,ICHD. Nantes:ICHD 2008 Local Organizing Committee, 2008:237-244. [4] Newman J N. Wave effects on deformable bodies [J].AppliedOceanResearch, 1994,16(1):47-59. [5] Lee C H, Newman J N. An assessment of hydroelasticity for very large hinged vessels [J].JournalofFluidsandStructures, 2000,14(7):957-970. [6] Diamantoulaki I, Angelides D C. Analysis of performance of hinged floating breakwaters [J].EngineeringStructures, 2010,32(8):2407-2423. [7] Hong S Y, Kim J H, Cho S K,etal. Numerical and experimental study on hydrodynamic interaction of side-by-side moored multiple vessels [J].OceanEngineering, 2005,32(7):783-801. [8] Kim B W, Hong S Y, Kyoung J H,etal. Investigation on wave reduction performances of floating hinge-linked breakwater [J].JournalofOceanScienceandTechnology, 2006,3(1):13-22. [9] 勾 莹,滕 斌,宁德志. 波浪与两相连浮体的相互作用[J]. 中国工程科学, 2004,6(7):75-80. GOU Ying, TENG Bin, NING De-zhi. Interaction effects between wave and two connected floating bodies [J].EngineeringScience, 2004,6(7):75-80. (in Chinese) [10] Tajali Z, Shafieefar M. Hydrodynamic analysis of multi-body floating piers under wave action [J].OceanEngineering, 2011,38(17):1925-1933. [11] 沈 庆,陈徐均. 系泊多浮体系统流固耦合和浮体间耦合动力分析[J]. 中国造船, 2002,43(2):81-84. SHEN Qing, CHEN Xu-jun. Dynamic analysis of a mooring multi-body system coupled with fluid and among bodies [J].ShipBuildingofChina, 2002,43(2):81-84. (in Chinese) [12] Sun L, Eatock T R, Choo Y S. Responses of interconnected floating bodies [J].TheIESJournalPartA:Civil&StructuralEngineering, 2011,4(3):143-156. [13] Sun L, Eatock T R, Choo Y S. Multi-body dynamic analysis of float-over installations [J].OceanEngineering, 2012,51:1-15. [14] John F. On the motion of floating bodies II. Simple harmonic motions [J].CommunicationsonPureandAppliedMathematics, 1950,3(1):45-101. Motionresponsesofhingedmultiplefloatingbodiesunderregularwaveaction WANG Gui-bo, GOU Ying*, TENG Bin, CAO Guang-lei ( State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China ) Motion responses of hinged multiple floating bodies in regular waves are studied by modal analyses in frequency domain based on the linear potential flow theory. Hydrodynamic coefficients and exciting forces are obtained by solving the boundary integral equations, which are developed by boundary element method. The system motion equations for solving motion amplitude response of motion modals are established by the adoption of constrained matrix, which is derived by the principle of minimum potential energy and the method of Lagrange multipliers. The validity and effectiveness of the presented method is verified by a satisfactory agreement with published results of motion responses of five hinged floating barges under regular waves. At last, taking three hinged floating barges as examples, the influences of water depth and hinged position on motion response are discussed, respectively. The experimental results show that water depth and hinged position have certain impact on the motion response of the structure, and for the different wave periods, the influences are different. higher-order boundary element method; hinged connection; multiple floating bodies; motion responses 1000-8608(2014)06-0618-08 2014-01-09; : 2014-09-20. 创新研究群体科学基金资助项目(51221961);“九七三”国家基础研究发展计划资助项目(2013CB036101);中央高校基本科研业务费专项资金资助项目(DUT14ZD203). 王桂波(1987-),男,硕士生;勾 莹*(1977-),女,讲师,E-mail:gouying@dlut.edu.cn;滕 斌(1958-),男,教授,博士生导师. O35 :Adoi:10.7511/dllgxb201406004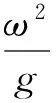
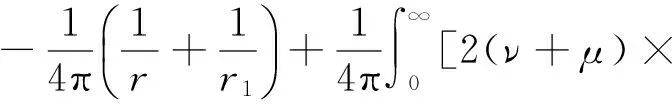
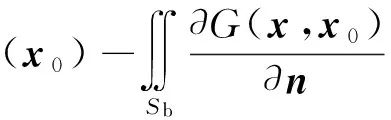
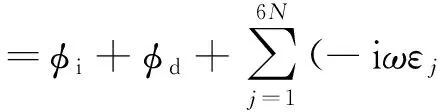
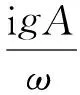
2 运动方程的建立
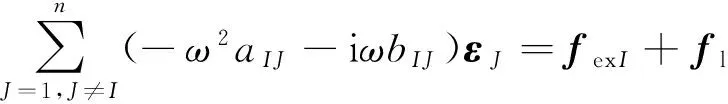
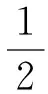
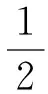
3 数值验证及分析
4 结 论
