框支-斜交密肋复合墙结构影响因素及框支梁内力系数研究

贾 穗 子， 袁 泉， 曹 万 林

( 1.北京工业大学 建筑工程学院， 北京 100124；2.北京交通大学 土木建筑工程学院， 北京 100044 )



框支-斜交密肋复合墙结构影响因素及框支梁内力系数研究

贾 穗 子*1， 袁 泉2， 曹 万 林1

( 1.北京工业大学 建筑工程学院， 北京 100124；2.北京交通大学 土木建筑工程学院， 北京 100044 )

采用正交试验设计方法，考虑框支梁高跨比(hb/l0)、抗震墙截面宽度与高度比(Bw/Hw)、密肋复合墙高跨比(hw/l0)，通过对框支-斜交密肋复合墙结构计算结果直观分析和方差分析，对构件关键部位内力和整体结构最大转角影响因素进行显著性分析，得出hb/l0和Bw/Hw对框支梁和框支柱的部分内力具有显著影响，对整体结构最大转角具有一定影响的结论．并在此基础上给出相应框支梁内力系数实用设计计算方法．

框支-斜交密肋复合墙；框支梁；正交试验设计；内力系数

0 引 言

框支-斜交密肋复合墙结构底部采用框架-剪力墙结构形式，上部选用新型斜交肋格的密肋复合墙结构．密肋复合墙结构具有节能抗震、绿色环保、轻质高强、施工简单、刚度灵活可调的特点[1-5]，其中密肋复合墙板是由密布的肋梁、肋柱构成肋格，内嵌生态轻质砌块预制而成的板式构件,混凝土边框柱、连接柱及暗梁组成的外框架连接、约束着密肋复合墙板，形成密肋复合墙结构的主要受力构件[6]．以往密肋复合墙板采用正交肋格的构造形式，本文首次选用斜交框格改变墙体传力途径，沿斜向裂缝方向向下传力同时减轻砌块的阻碍作用，使得上下层受力更均匀，构造形式具有创新性．

对框支-斜交密肋复合墙结构低周反复加载试验研究及运用非线性动力分析程序IDARC和ANSYS对试件的滞回特性、受力性能有限元分析表明，框支-斜交密肋复合墙结构同框支-砌体结构和框支-剪力墙结构相比[7]，表现出不同的受力特性，因此对该结构构件实用计算方法研究具有必要性．本文基于IDARC建立结构模型，采用正交试验设计方法研究多种因素对构件内力和顶部最大转角影响的显著性，由统计回归得到框支梁的预测数学模型．

1 框支-斜交密肋复合墙结构分析中试件正交试验设计

按照试件(基本构造形式见图1)尺寸，取框支梁跨度l0为6 m,抗震墙高度Hw为1.75 m，分别考虑hb/l0、Bw/Hw和hw/l0三个因素分析结构框支梁、框支柱弯矩和剪力及顶部最大转角．在正交试验水平表表头设计中，放置一个空白列作为误差列，以防因素交互对试验结果造成误差[8]． 正交试验设计水平表的设置见表1，依据各因素水平数，安排试验方案，具体参数设置见表2．

图1 框支-斜交密肋复合墙结构示意图

表1 试件正交试验设计水平表

表2 试件正交试验表

2 影响因素直观分析

由表2设计的9组正交试验经有限元分析，分别得出框支梁、框支柱关键部位的剪力、弯矩及整体结构顶部最大转角，见表3．

基于表3的计算结果，表4给出运用极差法对影响因素和空白列的直观分析．其中Ki表示某一列取第i个水平时的所有内力试验值之和；ki=Ki/ni，表示该因素在相应水平上内力试验值的平均数，其中ni表示第i列同一水平出现的次数，即试验次数除以第i列水平数；Ri=max(ki)-min(ki)，表示第i列的极差．

由表4可知：框支梁支座剪力空白列极差与因素hw/l0极差相当，说明对于支座的空白列表面上虽然没有安排因素，但实际上存在一些“因素”，这些“因素”与其他影响因素发生交互作用，试验本身的人为、机械误差也会导致空白列极差增大，由于空白列极差没有大于某因素的极差，排除遗漏对试验结果有重要影响的因素．其余内力空白列极差均小于其他因素．综上所述，本文对于创新型框支-斜交密肋复合墙结构因素安排合理，在误差范围以内．

表3 正交试验计算结果

表4 墙体直观分析表

图2给出影响构件内力和转角各因素水平(L)与同水平平均偏差量的趋势图．

由图2可知，对于框支梁内力变化，hb/l0影响最大，Bw/Hw次之，hw/l0较小, 且随因素水平的增加内力呈增大趋势；对于框支柱底部剪力，Bw/Hw影响最大，hb/l0、hw/l0次之，且随hw/l0递增呈下降趋势；hb/l0对框支柱底部弯矩影响较大，Bw/Hw次之，hw/l0最小．对于试件顶部最大转角的影响，3个因素极差相差不大，随着因素水平增加，折线曲率比较缓和．

(a) 框支梁支座剪力影响趋势图

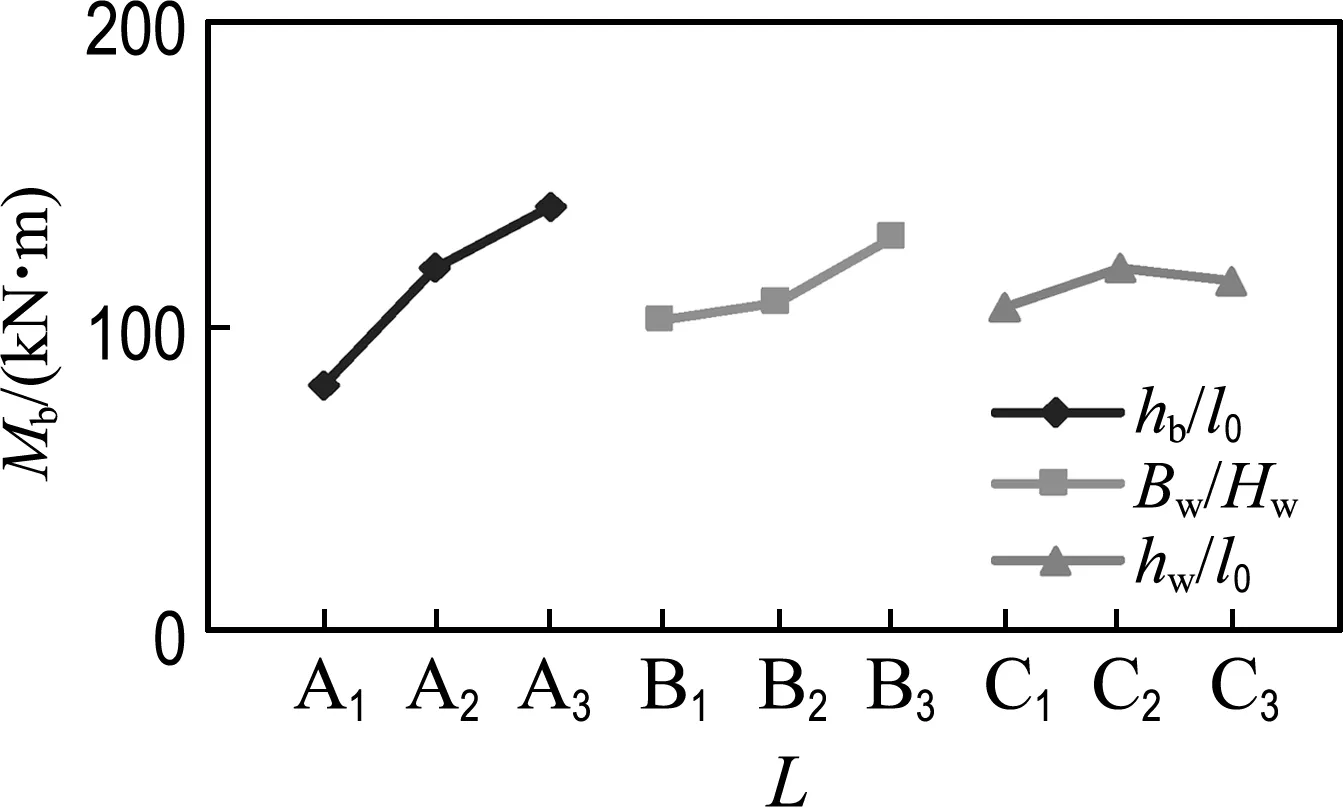
(b) 框支梁支座弯矩影响趋势图

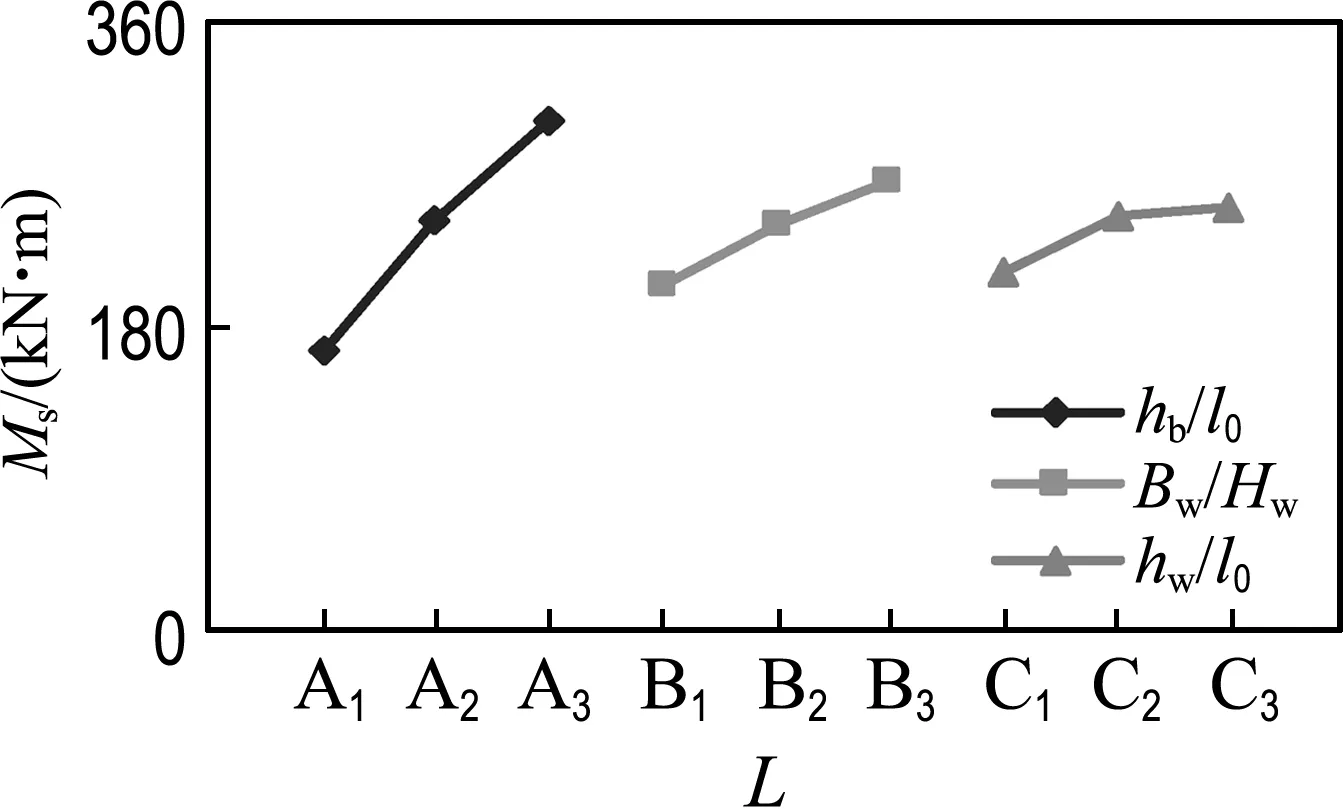
(c) 框支梁跨中弯矩影响趋势图

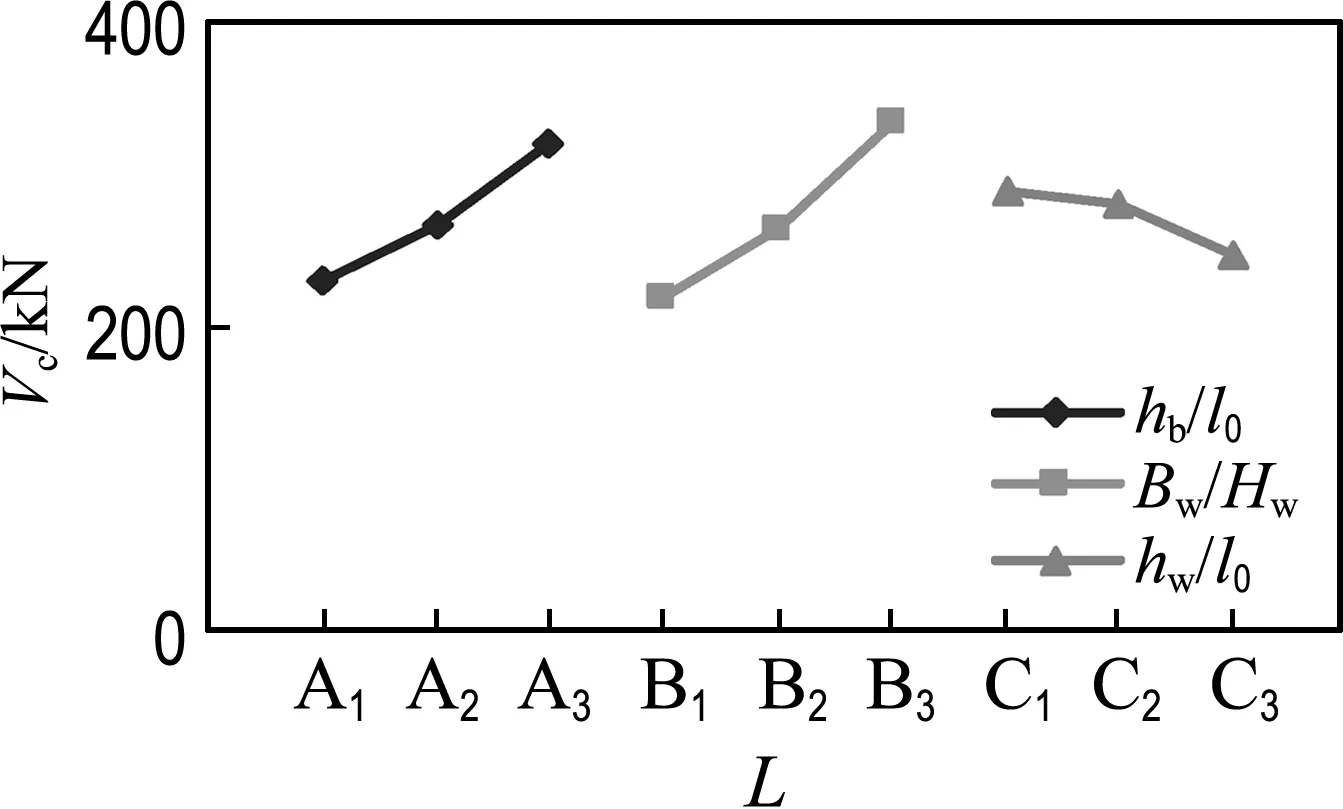
(d) 框支柱底部剪力影响趋势图

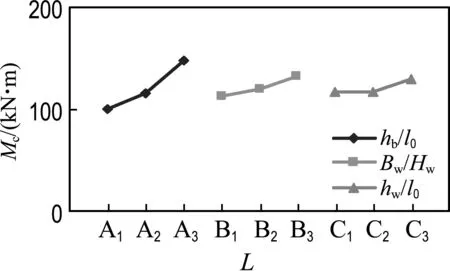
(e) 框支柱底部弯矩影响趋势图

(f) 顶点最大转角影响趋势图

图2 各因素水平与同水平平均偏差量的影响趋势

Fig.2 The influence trend of factor level and average deviation value of the same level

3 影响因素方差分析

采用方差分析法对正交试验计算结果进行精确分析，表5给出各因素对框支梁、框支柱内力及墙体最大转角的显著性程度的判定．

各因素对结构内力的影响服从自由度为(2,2)的F分布．当F≥F0.01(2,2)=99时，说明因素水平的改变对指标影响特别显著，即该因素为高度显著因素，记作***；当F0.01(2,2)>F≥F0.05(2,2)=19时，说明因素水平的改变对指标影响显著，即该因素为显著因素，记作**；当F0.05(2,2)>F≥F0.10(2,2)=9时，说明因素水平的改变对指标有一定影响，即该因素为一定影响因素，记作*；当F0.10(2,2)>F时，说明因素水平的改变对指标无显著影响，即该因素为非显著性因素，记作×．F值与对应临界值之间的差距越大，说明该因素越重要．

表5 方差分析F值计算表

由表5可知，对于框支梁支座剪力，hb/l0具有高度显著影响，Bw/Hw影响显著，hw/l0影响显著性不大；对于支座弯矩，hb/l0、Bw/Hw具有高度显著影响，其中hb/l0影响效应比重更大，hw/l0是非显著性影响因素；hb/l0、Bw/Hw、hw/l0均为跨中弯矩的影响因素，hb/l0影响最显著；对于框支柱底部弯矩和剪力，3个因素均为影响因素，而框支柱内力的显著影响因素不同，底部剪力为Bw/Hw，底部弯矩为hb/l0；对于顶点最大转角，hb/l0和Bw/Hw具有一定影响．

4 框支梁内力系数分析

由于框支-斜交密肋复合墙体属于新型结构，斜向交叉的肋格改变了以往墙板传力途径，不受砌块阻隔，沿主应力方向传力，在墙板上开洞，洞口两侧构造柱受力极其复杂，容易发生破坏，且理论基础和试验数据较少，所以本文暂时不研究洞口对斜交框支密肋结构的影响．本文参照框支砌体结构实用设计计算方法[9]，推导框支-斜交密肋复合墙结构中框支梁内力系数．

等效竖向荷载直接作用在框架梁顶面时，底部框剪结构框架梁内力计算结果列于表6，为了便于对比分析，框支-斜交密肋复合墙结构中框支梁内力计算结果也列于其中．

(1)框支梁跨中截面弯矩系数αM

为了便于实用设计计算，在回归框支梁跨中截面系数αM时仅考虑最显著因素，即高跨比hb/l0，基于表6数据，偏于安全考虑，对于每一种因素水平，选取αM最大的数据组进行回归分析．最终得出αM关于hb/l0的计算公式，如下式所示：

αM=1.97hb/l0+0.46

(1)

对于式(1)，所选取的hb/l0、αM数据组，其计算值与有限元值之比，μ=1.062，σ=0.061，δ=0.057，R2=0.999．

表6 框支-斜交密肋复合墙结构框支梁与相应框架梁正交设计内力计算结果对比分析

(2)框支梁支座截面弯矩系数α′M

框支梁支座截面弯矩系数α′M计算原理同式(1)．参见表5和6，虽然hb/l0影响效应比重是Bw/Hw的3倍多，但是hb/l0和Bw/Hw均对支座弯矩产生高度显著影响，对于两种因素的每一种水平，选取α′M最大的数据组进行回归分析．最终分别得出α′M关于hb/l0、Bw/Hw的计算公式如式(2)和(3)所示：

α′M1=-1.68hb/l0+0.95

(2)

式(2)中，相应的hb/l0、α′M1数据组，其计算值与有限元值之比，μ=1.097，σ=0.114，δ=0.104，R2=0.922．

α′M2=-0.84Bw/Hw+0.65

(3)

式(3)中，相应的Bw/Hw、α′M2数据组，其计算值与有限元值之比，μ=0.673，σ=0.072，δ=0.107，R2=0.997．

(3)框支梁支座截面剪力系数βV

参见表5和6，hb/l0是最显著因素，对于每一种因素水平，选取支座截面βV最大的数据组进行回归分析，最终得出βV关于hb/l0的计算公式，如下式所示：

βV=-1.76hb/l0+1.11

(4)

式(4)中，相应的所有hb/l0、βV数据组，其计算值与有限元值之比，μ=1.087，σ=0.117，δ=0.108，R2=0.993．

5 结 语

本文考虑框支梁高跨比、抗震墙截面宽度与高度比、密肋复合墙高跨比三因素影响，采用正交试验设计，并通过设置空白列以减小对新型结构没有足够认知带来的误差，对框支-斜交密肋复合墙结构进行了研究．基于对结果的直观分析和方差分析，得出影响结构框支梁、框支柱内力和整体最大转角的各因素水平与同水平平均偏差量变化趋势，及影响因素的显著程度．在此基础上，考虑影响最显著因素，通过回归分析拟合框支梁内力系数计算公式，为相关结构设计提供了参考．

[1] 黄 炜,张程华,姚谦峰,等. 密肋壁板结构弹塑性计算模型研究[J]. 振动与冲击, 2011,30(2):233-237.

HUANG Wei, ZHANG Cheng-hua, YAO Qian-feng,etal. Elasto-plastic models of a multi-ribbed slab structure [J].JournalofVibrationandShock, 2011,30(2):233-237. (in Chinese)

[2] 夏 雷,丁永刚,姚谦峰. 框支密肋复合墙结构墙梁抗震性能试验研究[J]. 建筑结构学报, 2011,32(10):146-152.

XIA Lei, DING Yong-gang, YAO Qian-feng. Experimental study on seismic performance of multi-ribbed composite wall-beam supported on frame [J].JournalofBuildingStructure, 2011,32(10):146-152. ( in Chinese)

[3] 贾穗子,袁 泉. 密肋复合墙结构滞回退化参数及耗能减震性能[J]. 华中科技大学学报, 2013,41(7):32-35.

JIA Sui-zi, YUAN Quan. Deteriorating hysteretic parameters and energy dissipation performance of multi-ribbed composite wall structures [J].JournalofHuazhongUniversityofScienceandTechnology, 2013,41(7):32-35. (in Chinese)

[4] LIU Pei, YAO Qian-feng. Dynamic reliability of structures:the example of multi-ribbed composite walls [J].StructuralEngineeringandMechanics, 2010,36(4):463-479.

[5] 贾穗子,袁 泉. 近断层地震动作用下密肋复合墙结构地震反应分析[J]. 哈尔滨工程大学学报, 2012,33(11):1366-1370.

JIA Sui-zi, YUAN Quan. Seismic response analysis of multi-ribbed composite wall structure subjected to near-fault ground motions [J].JournalofHarbinEngineeringUniversity, 2012,33(11):1366-1370. (in Chinese)

[6] 贾穗子,姚谦峰. 近场地震作用下密肋耗能复合墙结构地震响应分析[J]. 北京交通大学学报, 2011,35(4):88-92.

JIA Sui-zi, YAO Qian-feng. Seismic response analysis of multi-ribbed energy-dissipated composite wall structure of near-field ground motions [J].JournalofBeijingJiaotongUniversity, 2011,35(4):88-92. (in Chinese)

[7] 贾穗子. 框支密肋复合板结构抗震性能研究[D]. 北京:北京交通大学, 2014.

JIA Sui-zi. Research on seismic performance of frame-supported multi-ribbed composite slab structure [D]. Beijing:Beijing Jiaotong University, 2014. (in Chinese)

[8] 李云雁,胡传荣. 试验设计与数据处理[M]. 北京:化学工业出版社, 2005.

LI Yun-yan, HU Chuan-rong.ExperimentalDesignandDataProcessing[M]. Beijing:Chemistry Industry Press, 2005. (in Chinese)

[9] 中华人民共和国住房和城乡建设部. GB 50003—2011 砌体结构设计规范 [S]. 北京:中国建筑工业出版社, 2011.

Ministry of Housing and Urban-Rural Construction of the People′s Republic of China. GB 50003-2011 Code for Seismic Design of Masonery Structures [S]. Beijing:China Architecture Building Press, 2011. (in Chinese)

Researchoninfluencefactorofframe-supportedoblique-gridmulti-ribbedcompositewallandinternalforcecoefficientofframe-supportedbeam

JIA Sui-zi*1， YUAN Quan2， CAO Wan-lin1

( 1.The College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China；2.School of Civil Engineering and Architecture, Beijing Jiaotong University, Beijing 100044, China )

Considering the factors of height-to-span ratio (hb/l0) of the beam, width-to-height ratio (Bw/Hw) of the aseismic wall and height-to-span ratio(hw/l0) of multi-ribbed composite wall(MCW), the orthogonal test design method was adopted to analyze the calculation results of frame-supported oblique-grid MCW structure by using the visual and variance analyses, and the internal force influence factors of key parts and structural maximum angle were also researched. It is concluded thathb/l0andBw/Hwhave significant effects on part internal force of frame-supported beam and frame-supported column, as well as have certain effects on structural maximum angle, and based on the analytical results, the calculation method on internal force coefficient of frame-supported beam is obtained.

frame-supported oblique-grid multi-ribbed composite wall; frame-supported beam; orthogonal test design; internal force coefficient

1000-8608(2014)06-0612-06

2014-06-22；

: 2014-10-09．

“十二五”国家科技支撑计划资助项目(2011BAJ08B02)；国家自然科学基金资助项目(51078028).

贾穗子*(1984-)， 女，博士，在站博士后，E-mail: suizijia@163.com.

TU352.1

：Adoi:10.7511/dllgxb201406003