基于飞机散射信号的民航地面干扰源定位新算法

栾 声 扬， 邱 天 爽*， 于 玲， 李 景 春， 谭 海 峰

( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024；2.国家无线电监测中心，北京 100037；3.北京邮电大学 信息与通信工程学院， 北京 100876 )



电子与信息工程、管理工程

基于飞机散射信号的民航地面干扰源定位新算法

栾 声 扬1， 邱 天 爽*1， 于 玲1， 李 景 春2， 谭 海 峰3

( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024；2.国家无线电监测中心，北京 100037；3.北京邮电大学 信息与通信工程学院， 北京 100876 )

为了快速准确定位民航地面干扰源，提出了一种新的基于飞机散射信号的定位算法．首先，提出了新的初始参考点选取方法，并对此进行了理论分析和实验验证；然后，引入了相关熵和加权质心法，对现有算法进行了改进，同时进行了分析和实验验证．仿真实验结果表明，所提算法在保持计算量不变的前提下，显著地提升了基于飞机散射信号的民航地面干扰源定位精度，更具实用性．

干扰源定位；民航；多普勒频移；相关熵；加权质心法

0 引 言

民航通信安全是民航飞行安全的重要组成部分，按照国际民航组织(International Civil Aviation Organization，ICAO)规定，通常情况下采用频率范围为108 MHz到137 MHz的调幅(amplitude modulation，AM)广播为主要导航和通信方式，上述频率范围属于甚高频(vertical high frequency，VHF)频段[1]．在此频段，机载通信设备容易受到多种干扰[2]．根据干扰源的种类可以将其分为广播电台和有线电视台、大功率无绳电话、工科医射频设备、电力传输系统干扰等；而按照干扰产生的机制可以分为同频干扰、互调干扰、阻塞干扰和杂散辐射等．近年来，较常见的干扰源主要是非法的或设备老化的无线广播电台同频干扰、互调干扰．上述各类干扰是民航飞行作业严重的安全隐患，因此如何对影响民航通信的地面干扰源进行快速准确定位成为保障民航通信安全的重要课题．

针对民航地面干扰源的定位方法主要分为基于直达波方法和基于非直达波方法两大类．在这两大类方法中，基于直达波方法的研究比较成熟，其又分为地面监控和空中监控两种，具体而言，主要是基于接收信号强度(received signal strength，RSS)估计[3-4]、基于时延(time delay of arrival，TDOA)估计[5-6]和基于波达方向(direction of arrival，DOA)估计[7-8]．地面监控虽然成本较低，但易受地形地势影响，监测范围较小；而空中监控虽然具有较大的监测范围，但是成本较高．针对上述问题，谭海峰等[9]提出了利用飞机散射信号对地面干扰源进行定位的设想，并给出了相应的算法；邱天爽等[10]在此基础上，引入粒子滤波算法对民航干扰源的定位问题开展了研究．这两种算法都属于基于非直达波的民航地面干扰源定位算法，均可有效地解决在直达波信号较弱或者没有直达波情况下的定位问题，同时具有监测范围大、监控成本低的优点．但这两种算法仍存在不足，例如，文献[9]采用了正方形的区域划分方法来选取参考点，并且只利用最大相关值参考点对干扰源位置进行估计，导致定位误差较大；文献[10]在监测区域内引入大量粒子(即参考点)导致计算量较大，在较低信噪比时定位精度较差．

针对上述问题，本文提出一种新的基于飞机散射信号的民航地面干扰源定位算法．该算法采用正三角形划分监测区域，选取其各顶点作为初始参考点，并利用相关熵和加权质心法来估计干扰源的位置．

1 多普勒频移数学建模

民航地面干扰源发出的无线电信号经过飞机散射再被接收机获取的过程主要分为两个阶段，分别是信号由干扰源发射到达飞机的过程和信号由飞机散射后到达地面接收机的过程．在上述两个阶段中，飞机与干扰源之间、飞机与接收机之间都存在相对运动，故信号会发生多普勒频移，该频移与速度在相对运动的两者之间连线上的投影有关，而速度的投影又是时间变量的函数，故多普勒频移也是时间变量的函数，进而可以通过计算得到多普勒时频曲线．

依据大地坐标系理论[11]建立空间笛卡尔坐标系，将t时刻的飞机速度设为vp(t)=(vp,x(t)vp,y(t)vp,z(t))T，将飞机坐标设为xp(t)=(xp(t)yp(t)hp(t))T，将干扰源坐标设为xi=(xiyihi)T，将接收机坐标设为xr=(xryrhr)T，并且记光速为c0，干扰源信号载波频率为fc．其中，飞机的位置和速度信息可由广播式自动相关监视报文获取，接收机坐标以及接收信号的时间戳可由全球定位系统获取．

干扰源信号上行到达飞机处的载频fup(t)称为上行载频，根据多普勒频移的相关理论，它满足

(1)

干扰源信号被飞机散射后下行到达接收机处的载频fdown(t)称为下行载频，它满足

(2)

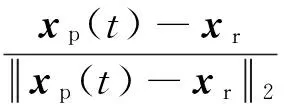
在接收机处得到的干扰源信号所包含的多普勒频移fD(t)为

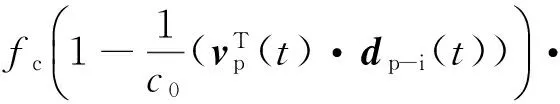
(3)

式(3)表示关于时间变量的多普勒频移函数，由式(3)可计算理论多普勒时频曲线．

2 定位算法与分析

2.1 定位算法

现有的民航干扰源定位算法流程可以分为3个阶段，即建立数学模型、选择初始参考点，以及基于不同准则筛选参考点．在选择初始参考点阶段，如图1(a)所示，文献[9]以正方形划分整个监测区域，并以各正方形的顶点作为初始参考点，文献[10]则在监测区域内随机选取大量的粒子作为初始参考点；在筛选参考点阶段，文献[9]采用最大相关值法，并以此作为选择最优点的依据，文献[10]则基于最小均方误差(MMSE)为每一个粒子选取了不同的权重，并以权重作为衡量参考点重要性的依据．

如图1(b)所示，本文在选择初始参考点阶段以正三角形对监测区域进行划分，并以其顶点作为参考点；在筛选参考点阶段，本文引入了相关熵的方法，并且只利用筛选出的少数参考点通过加权质心法来对干扰源位置进行估计．

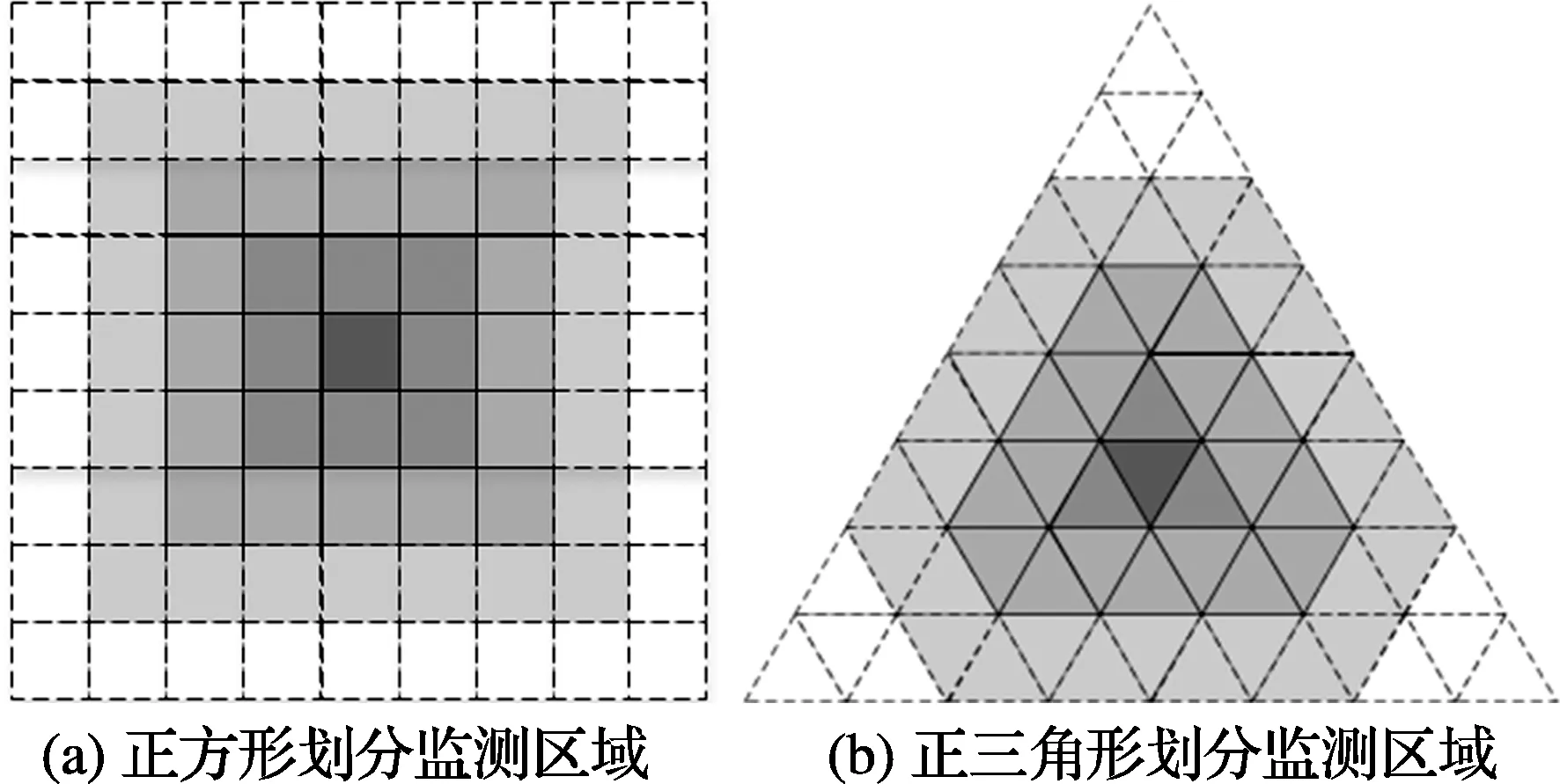
图1 监测区域按照正方形或正三角形划分

首先用正三角形划分监测区域，选取顶点作为初始参考点，其坐标记为xi,j=(xi,jyi,jhi,j)T，其中j=1,2,…,N，N表示整个区域的参考点总数．再将初始参考点坐标xi,j代入式(3)，可以计算得到对应于每个初始参考点的多普勒频移函数，记作fD,j(t)，其中j=1,2,…,N．设接收机所接收到零中频散射信号可以分成IQ两路sI(t)和sQ(t)，即

sI(t)=a(t)cos[φ(t)]

sQ(t)=a(t)sin[φ(t)]

(4)

其中a(t)是信号的包络，φ(t)是信号的相位．

设散射信号的多普勒频移函数为fD(t)，则有

(5)

将fD,j(t)和fD(t)代入式(6)，计算对应的相关熵vj，其中j=1,2,…,N，则有

vj=E[к(fD,j(t)-fD(t))]

(6)

式中：E[·]表示数学期望；к(·)是核函数，在此选用高斯核函数：

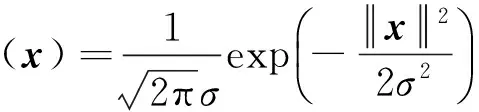
(7)

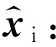
(8)

其中权值

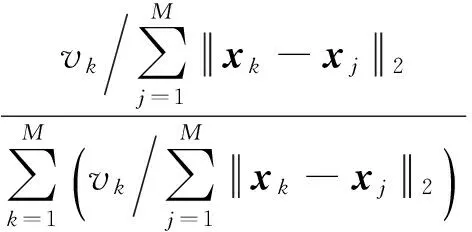
(9)

2.2 算法分析

不妨设用来划分监测区域的正多边形边数为n，每个内角为αn，单位为(°)，则αn能被360整除．由平面几何知识，αn取值范围为(0,180°)，并且随n的增大，αn也不断增大，故满足条件的αn只能取60°、90°和120°，即满足条件的正多边形为正三角形、正方形和正六边形．

在采用相同形状的正多边形划分同一个监测区域时，正多边形的面积越小，参考点的间距也越小，故定位精度就越高；而正多边形的面积越小，初始参考点的个数越多，故计算量就越大．因此，本文在选择正多边形时基于下列前提：监测区域的总面积S是相等的，初始参考点的个数均为N．满足上述条件下，只改变划分监测区域的多边形形状，定位算法计算量保持不变．

以正三角形为例，选取图1(b)中颜色较深的正三角形，如图2(a)所示，并以正三角形的中心B向任意一条边作垂线，交该边于垂足O，取该边上的一个顶点A，将此直角三角形记作△AOB．为了方便研究，如图2(b)建立笛卡尔直角坐标系．由于△AOB是正三角形的六等分之一，故△AOB被记作Δ3，并被称为采用正三角形划分区域时的基础三角形(下文简称基础三角形)．在此处和后文中，下角标处的正整数n表示对应的正多边形的边数，不再赘述．

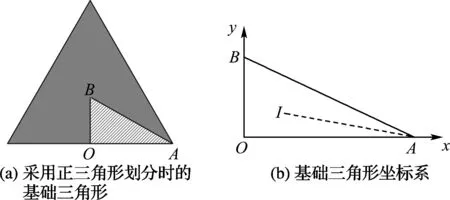
图2 采用正三角形划分时的基础三角形坐标系

假设干扰源I出现在图2(b)正三角形中的Δ3内，那么按照文献[9]算法，则会选择点A作为干扰源位置的最优估计，此时的定位误差为线段IA的长度|IA|，它的数学期望e3满足

|IA|]；n=3,4,6

(10)

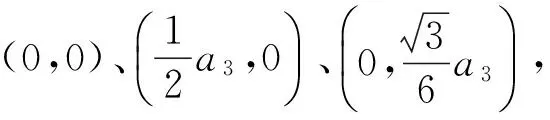
(11)

其中SΔ3表示基础三角形Δ3的面积．将ρ3(x,y)代入式(10)中，得到数学期望e3：

(12)

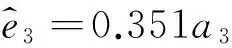
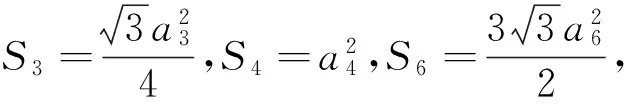
上述结论均基于最大相关值参考点估计法(文献[9]算法)，目的是为了确认哪种区域划分和初始参考点选择方式最有利于提高定位算法的精度．出于与之前的方法进行对比的目的，尚未引入相关熵和加权质心法，故在实验仿真阶段，不但要比较不同区域划分方法结合最大相关值参考点法时的定位精度，还要比较引入相关熵和加权质心法后的定位精度．

3 仿真结果

为了验证本文算法的有效性，实验仿真参数选取如下：在监测区域内随机选择干扰源坐标，设置接收机坐标为xr(t)=(4 300 500 0)T，设置飞机初始位置为xp(0)=(0 0 4 800)T，设置飞机的速度为vp(t)=(160 120 0)T，干扰源的载波频率为127 MHz，光速为3×108m/s，并选定边长为2×104m，总面积S=4×108m2的正方形区域为监测区域，取初始参考点数N=100，则分块个数N3=200，N4=100，N6=50，且对应的边长a3=2.149×103m，a4=2×103m，a6=1.755×103m．

为了比较本文算法与文献[9]算法在不同噪声下的定位精度，构造含有加性高斯白噪声的接收信号，并按照5 dB步长在-20 dB到20 dB范围内选取不同信噪比，再以1 000次仿真结果的均方根误差(root mean square error,erms)作为评价依据来检验各种算法的定位精度，结果如图3和4所示．

其中，图3(a)是在文献[9]算法基础上采用多种正多边形进行划分的结果，而图3(b)则是引入相关熵和加权质心法后的结果．图4是为了说明相关熵和加权质心法对定位精度的提升而进行的仿真对比结果．

由图3和4实验结果可见，无论是采用最大相关值参考点法，还是采用相关熵和加权质心法，以正三角形划分监测区域时均具有更好的定位精度；同时，在引入相关熵和加权质心法后，3种划分方式的新算法都具有更好的定位精度．故在选取初始参考点阶段选择正三角形划分监测区域，在估计干扰源位置阶段引入相关熵和加权质心法是最好的选择．

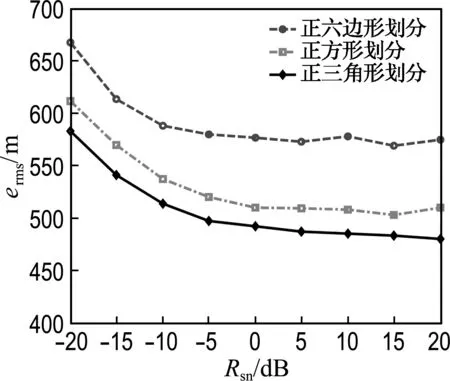
(a) 采用最大相关值参考点法时的均方根误差

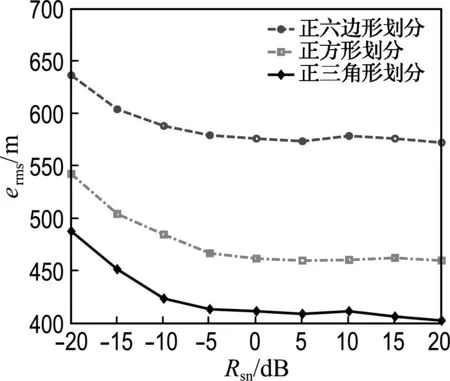
(b) 采用相关熵和加权质心法时的均方根误差

图3 不同划分方式时的定位均方根误差

Fig.3 Locating RMSE using different segmentations

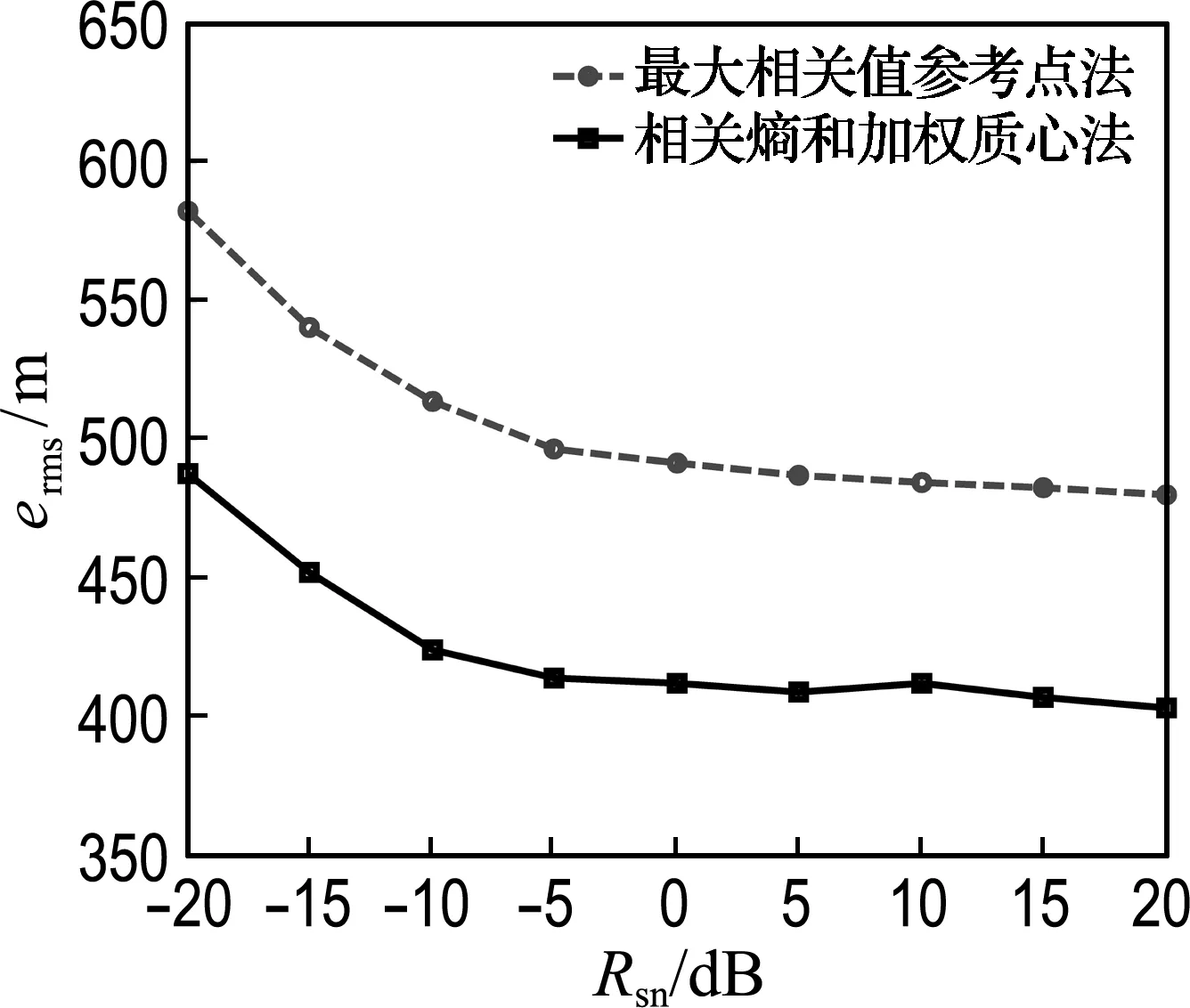
图4 采用正三角形划分时的定位均方根误差

需要说明的是，按照文献[10]中粒子滤波的定位算法，在选择初始参考点阶段选取了800个粒子，而在之后的每个时间点，都要基于800个点的数量进行权值更新，故计算量远远大于本文算法，因而在本文中只进行简要的说明和分析，而略去仿真比较．

4 结 语

本文针对威胁民航通信安全的地面干扰源定位问题，提出了一种新的基于飞机散射信号的干扰源定位算法．通过仿真实验，证明在高斯白噪声的条件下，本文算法定位精度较高．与文献[9]、[10]算法相比，本文算法的计算复杂度较小或者保持一致，这对实时分析并定位干扰源有实际应用价值．

[1] 马存宝. 民机通信导航与雷达[M]. 西安:西北工业大学出版社, 2004.

MA Cun-bao.CivilAircraftCommunicationNavigationandRadar[M]. Xi′an:Northwestern Polytechnical University Press, 2004. (in Chinese)

[2] Womersley R, Tournadre C, Hodder P. Investigation of interference sources and mechanisms for Eurocontrol. Final Report, DA243D005-1.0 [R]. Hull:Smith System Engineering Limited, 1997.

[3] So Hing-cheung, Lin Lan-xin. Linear least squares approach for accurate received signal strength based source localization [J].IEEETransactionsonSignalProcessing, 2011,59(8):4035-4040.

[4] WANG Gang, YANG Ke-hu. A new approach to sensor node localization using RSS measurements in wireless sensor networks [J].IEEETransactionsonWirelessCommunications, 2011,10(5):1389-1395.

[5] HU Jin-wen, XIE Li-hua, XU Jun,etal. TDOA-based adaptive sensing in multi-agent cooperative target tracking [J].SignalProcessing, 2014,98:186-196.

[6] Lin Lan-xin, So Hing-cheung, Chan F K W,etal. A new constrained weighted least squares algorithm for TDOA-based localization [J].SignalProcessing, 2013,93(11):2872-2878.

[7] 李 丽,邱天爽. 双基地 MIMO 雷达收发角和多普勒频率参数的联合估计方法[J]. 电子学报, 2013,41(12):2462-2467.

LI Li, QIU Tian-shuang. An algorithm for DOD-DOA and Doppler parameters jointly estimating in bistatic MIMO radar system [J].ActaElectronicaSinica, 2013,41(12):2462-2467. (in Chinese)

[8] ZHANG Jin-feng, QIU Tian-shuang. A novel covariation based noncircular sources direction finding method under impulsive noise environments [J].SignalProcessing, 2014,98:252-262.

[9] 谭海峰,李景春. 利用飞机散射信号查找干扰源的定位算法[J]. 无线电通信技术, 2009,35(2):40-42.

TAN Hai-feng, LI Jing-chun. Emitter locating algorithm by scattered signals of civil airplanes [J].RadioCommunicationsTechnology, 2009,35(2):40-42. (in Chinese)

[10] 邱天爽,夏 楠,李景春,等. 稳定分布噪声下基于高斯近似粒子滤波的干扰源定位算法[J]. 信号处理, 2012,28(9):1248-1253.

QIU Tian-shuang, XIA Nan, LI Jing-chun,etal. An interference localization algorithm based on Gaussian approximation particle filtering with stable distribution noise [J].JournalofSignalProcessing, 2012,28(9):1248-1253. (in Chinese)

[11] Snay R A, Soler T. Modern terrestrial reference systems PART 3:WGS 84 and ITRS [J].ProfessionalSurveyor, 2000,20(3):1-3.

Anovelalgorithmforcivilaviationgroundinterferencesourcelocatingviaplanescatteredsignals

LUAN Sheng-yang1， QIU Tian-shuang*1， YU Ling1， LI Jing-chun2， TAN Hai-feng3

( 1.Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China；2.The State Radio Monitoring Center, Beijing 100037, China；3.School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China )

A novel algorithm is proposed to locate the civil aviation ground interference source accurately and effectively via plane scattered signals. Firstly, a new method of arranging initial reference points is raised which is analyzed theoretically and testified experimentally. Secondly, correntropy and weighted centroid are introduced to optimize the existing locating algorithm. Both analyses and experiments are carried out. Simulation results show that the proposed algorithm improves the locating accuracy significantly and it has better practicality under equal amount of computations.

interference source locating; civil aviation; Doppler frequency shift; correntropy; weighted centroid

1000-8608(2014)06-0626-06

2014-02-13；

: 2014-08-04．

国家自然科学基金资助项目(61139001,61172108,81241059).

栾声扬(1983-)，男，博士生，E-mail:luanshengyang@live.com；邱天爽*(1954-)，男，教授，博士生导师，E-mail:qiutsh@dlut.edu.cn.

TN911.72

：Adoi:10.7511/dllgxb201406005