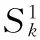按Laplace谱半径对一些偶单圈图的排序
2014-09-07张海霞
张 海 霞
( 1.大连理工大学 数学科学学院, 辽宁 大连 116024;2.太原科技大学 数学系, 山西 太原 030024 )
按Laplace谱半径对一些偶单圈图的排序
张 海 霞*1,2
( 1.大连理工大学 数学科学学院, 辽宁 大连 116024;2.太原科技大学 数学系, 山西 太原 030024 )
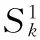
单圈图;最大Laplace特征值;排序
0 引 言
设G是n阶连通简单图,其顶点集为V(G)={v1,v2,…,vn},边集为E(G)={e1,e2,…,en}.G的阶数是指G的顶点个数.G的Laplace矩阵定义为L(G)=D(G)-A(G),其中A(G)和D(G)分别为G的邻接矩阵和度对角矩阵.G的Laplace特征多项式为Φ(G)=det(xI-L(G)),它的根称为G的Laplace特征值.既然L(G)是半正定的实对称矩阵,其所有的特征值都是实数,不妨记为μ1(G)≥…≥μn(G)=0,其中μ1(G)也称为G的Laplace谱半径.
图的Laplace特征值的研究是非常活跃的研究课题,已经有许多结果[1-5],它的研究不仅对图论本身有意义,而且对其他学科,例如物理、化学、生物也有非常重大的意义,因而越来越受到人们的关注[4-7].
单圈图是边数等于顶点数的简单连通图,它可以看成是树在不相邻的两个顶点间连一条边得到的.如果单圈图的圈长为偶数, 也称单圈图为偶单圈图.单圈图的邻接谱和Laplace谱的研究已有许多[8-9].而对于阶数和圈长固定的单圈图的Laplace谱半径的最小值问题仍未考虑.这里先考虑一些特殊的偶单圈图的Laplace谱半径的最小值问题.

1 用到的引理
引理1[11]记Dn是n阶矩阵,它是从路Pn+2对应的L(Pn+2)(n≥1)中删掉两个悬挂点所对应的行和列后得到的矩阵,其特征多项式记为Φ(Dn),规定Φ(D0)=1,Φ(D-n)=0.则
(1)xΦ(Dn-1)=Φ(Pn);
(2)Φ(Dn+1)=(x-2)Φ(Dn)-Φ(Dn-1);
(3)Φ(Dm+1)Φ(Dn)-Φ(Dm)Φ(Dn+1)=Φ(Dm)Φ(Dn-1)-Φ(Dm-1)Φ(Dn);
(4)Φ(Cn)=Φ(Dn)-Φ(Dn-2)+2(-1)n+1.

引理2给定n阶矩阵Dn(n≥1),则Φ2(Dn)=Φ(Dn+1)Φ(Dn-1)+1.
证明由引理1(2)可知,

两边取行列式可得
Φ2(Dn)-Φ(Dn+1)Φ(Dn-1)=Φ2(Dn-1)-Φ(Dn)Φ(Dn-2)=…=Φ2(D1)-Φ(D2)Φ(D0)=1
引理3给定n阶矩阵Dn(n≥1),则当x≥4时,Φ(Dn)>Φ(Dn-1).
证明利用数学归纳法:
当k=1时,Φ(D1)=x-2,Φ(D0)=1,故当x≥4时,Φ(D1)>Φ(D0).
假设当k≤n时,Φ(Dk)>Φ(Dk-1).
当k=n+1时,由引理1(2)及假设知,
Φ(Dn+1)-Φ(Dn)=(x-3)Φ(Dn)-Φ(Dn-1)> (x-4)Φ(Dn-1)≥0
故结论成立.
下面给出单圈图的一些变换性质.


证明不妨用k表示任意的大于3的正整数,由引理1(4)及文献[10]中引理1知,

(1)

当x≥r2时,P(x,k)>0;由引理3知P(4,k)<0;进一步
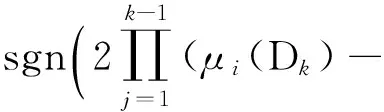

其中sgn为实数集R上的符号函数,即
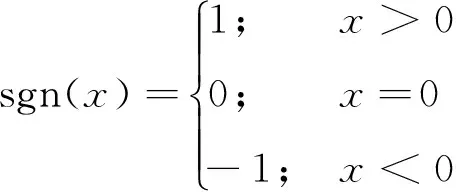
情形1若存在指标m满足μm(Dk-1)=r1,那么
由Φ(Dk)的根的特点可知1 情形2若存在指标m满足μm+1(Dk)≤r1<μm(Dk-1),那么sgn(P(μm+1(Dk),k))=(-1)m, sgn(P(μm(Dk-1),k))=(-1)m-1,因此P(x,k)在区间(μm+1(Dk),μm(Dk-1))内至少有一个实根,取代了情形1中的实根r1,其他区间内根的情况类似于情形1. 情形3若存在指标m满足μm+1(Dk-1) 综上,P(x,k)至少有k+1个实根,而P(x,k) 是k+2次多项式,故其余的根必定是实数.下面说明P(x,k)在(4,r2)内仅有一个根c(k),且为P(x,k)的最大根.不然,若(4,c(k)]内还有一个根d,由P(x,k)的连续性及根的分布特点可知,当x∈(4,d)时,P(x,k)<0,与P(x,k)>0矛盾.由此可见,P(x,k)的第二大根是小于4的. 下面考虑P(x,k)的最大根c(k)随k严格递减且有下界. 由Maple计算可知,c(4)=4.385 7,c(5)=4.384 7,故c(4)>c(5),假设c(k-1)>c(k)成立,由于P(x,k+1)-(x-2)P(x,k)=-P(x,k-1),等式两边取x=c(k),由假设可知,c(k)>c(k+1). 此外,P2(x,k)-P(x,k-1)P(x,k+1)=(x-4)(x3-6x2+8x-4),由Maple计算得到x3-6x2+8x-4=0的最大根为e=4.383 7,若存在l,使得c(l)≤e 证明通过直接计算可得 (2) 由于Dk-2-2a的最大特征值小于4,由文献[10]的引理6知,当 时,式(2)大于零,从而结论成立. (3) 其中a+b=k-2.特别地,当a=1,有以下定理. 证明不妨设k为任意的大于4的正整数,由式(3)可知 (4) 当x≥5时,Q(x,k)>0;由引理1(2)知Q(4,k)<0,考虑s1在区间(μk(Dk),μ1(Dk))内的位置. 若存在指标m满足μm(Dk)=s1,那么由Φ(Dk)的根的特点可知1 而Q(x,k)的最大根d(k)随k严格递增且有上界. 由Maple计算可知,d(4)=4.379 9,d(5)=4.382 8,故d(4) 此外,Q2(x,k)-Q(x,k-1)Q(x,k+1)=-x(x3-6x2+8x-4),由Maple计算得到x3-6x2+8x-4=0最大根为e=4.383 7,若存在m,使得d(m)≥e>d(m-1),那么Q2(x,m)-Q(x,m-1)Q(x,m+1)|x=e>0,与-x(x3-6x2+8x-4)|x=e=0矛盾.因而,d(k)严格递增且有上界e,但永远达不到上界. 证明由引理1(2)和2,式(3)变为 (5) 令W(x,t)=Φ(Dt)-2Φ(Dt-1)=(x-4)Φ(Dt-1)-Φ(Dt-2),t≥2. 由引理3知,对任意的x≥5,W(x,t)>0;W(4,t)<0.进一步, 由连续函数的零点定理知,W(x,t)在每个区间(μt(Dt),μt-1(Dt-1)),…,(μ2(Dt),μ1(Dt-1)),(4,5)内至少有一个实根,而W(x,t)的次数恰好为t,因而W(x,t)的第二大根小于4,记它的最大根为w(t). W(x,t)的最大根w(t)随t严格递增且有上界. 由Maple计算可知,w(1)=4,w(2)=4.415 0,故w(1) 此外,W2(x,t)-W(x,t-1)W(x,t+1)=9-2x,其最大根为4.5,若存在n,使得w(n)≥4.5>w(n-1),那么W2(x,n)-W(x,n-1)W(x,n+1)|x=4.5>0,与9-2x|x=4.5=0矛盾.因而,w(t)严格递增且有上界4.5,但永远达不到上界. 由定理1、2和引理5可知下面定理. [1]Anderson W N, Morley T D. Eigenvalues of the Laplacian of a graph [J]. Linear and Multilinear Algebra, 1985,18(2):141-145. [2]Cvetkovic D, Doob M, Sachs H. Spectra of Graphs-Theory and Application [M]. New York:Academic Press, 1980. [3]Kinkar C D. The Laplacian spectrum of a graph [J]. Computers and Mathematics with Applications, 2004,48(5-6):715-724. [4]LI Jiong-sheng, ZHANG Xiao-dong. A new upper bound for eigenvalues of Laplacian matrix of a graph [J]. Linear Algebra and Its Applications, 1997,265(1-3):93-100. [5]LI Jiong-sheng, ZHANG Xiao-dong. On the Laplacian eigenvalues of a graph [J]. Linear Algebra and Its Applications, 1998,285(1-3):305-307. [6]Merris R. Laplacian matrices of graphs:A survey [J]. Linear Algebra and Its Applications, 1994,197-198:143-176. [7]Merris R. A note on Laplacian graph eigenvalues [J]. Linear Algebra and Its Applications, 1998,285(1-3):33-35. [8]Cvetkovic D, Rowlinson P. Spectra of unicyclic graphs [J]. Graphs and Combinatorics, 1987,3(1):7-23. [9]郭曙光. 单圈图Laplace矩阵的最大特征值[J]. 高等应用数学学报:A辑, 2001,16(2):131-135. GUO Shu-guang. The largest eigenvalues of Laplacian matrix of unicyclic graphs [J]. Applied Mathematics Journal of Chinese Universities:Series A, 2001,16(2):131-135. (in Chinese) [10]张海霞,于洪全. 按Laplace谱半径对圈长和阶数固定的单圈图的排序[J]. 大连理工大学学报, 2013,53(1):145-150. ZHANG Hai-xia, YU Hong-quan. Unicyclic graphs ordering with fixed number vertices and cycle length by their Laplace spectral radii [J]. Journal of Dalian University of Technology, 2013,53(1):145-150. (in Chinese) [11]GUO Ji-ming. A conjecture on the algebraic connectivity of connected graphs with fixed girth [J]. Discrete Mathematics, 2008,308(23):5702-5711. [12]GUO Ji-ming. The Laplacian spectral radius of a graph under modifications [J]. Computers and Mathematics with Applications, 2007,54(5):709-720. Someeven-unicyclicgraphsorderingbytheirLaplacianspectralradii ZHANG Hai-xia*1,2 ( 1.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China;2.Department of Mathematics, Taiyuan University of Science and Technology,Taiyuan 030024, China ) unicyclic graphs; maximum Laplacian eigenvalues; ordering 1000-8608(2014)01-0152-05 2012-11-23; : 2013-09-21. 山西省自然科学基金资助项目(2012011019-2);太原科技大学校青年基金资助项目(20113022). 张海霞*(1979-),女,博士生,讲师,E-mail:zhx049@163.com. O157.5 :A 10.7511/dllgxb201401023
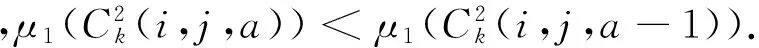


2 主要结论

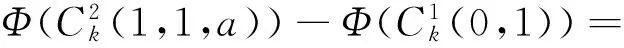






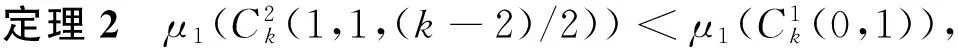





3 结 语