基于FFT算法的舰载导弹发射弹位影响研究

钟 洲, 姜 毅

(北京理工大学 宇航学院，北京 100081)

舰载导弹是现代海军的主要武器装备，为了保证火力强度，通常会在一艘舰船上不同位置配置多个共架发射系统。由于海战的特殊性，海浪的摇摆运动也会对导弹的发射精度产生影响[1]，表现在不同发射位置的导弹具有数值上较大差异的出筒姿态。因此，为了满足制导系统要求，对舰载导弹发射弹位影响的研究具有非常重要的意义。

本文利用Lagrange方程和修正的Craig-Bampton法建立了舰载导弹刚柔耦合发射动力学模型；通过参数化脚本语言(.cmd)[2]和C++编译程序，进行了参数化动力学仿真，获得了大量的导弹出筒姿态参数数据。同时，基于快速傅里叶变换法[3]对恶劣发射弹位导弹的动力学响应进行频谱分析，研究了发射精度的影响因素，并进一步分析了发射弹位对发射精度的影响，为舰载武器的设计和发射提供了参考依据。

1 快速傅里叶变换法

1.1 信号的频域处理方法

通常，我们利用试验或仿真得到的数据是时域信号，其反映的是不同时刻的响应情况。本文为了从舰艇运动方面来分析弹位对导弹发射精度的影响，需要进行时域信号的频域处理，显露出时域信号里隐藏的信息。目前，傅里叶变换是进行频域分析的重要手段，用于计算机处理的方法是离散傅里叶变换。

设有N点有限长序列x(n)，则其离散傅里叶变换(DFT)为

(1)

式中:k=0,1,2,…,N-1

逆变换(IDFT)为

(2)

1.2 FFT算法

假设DFT的抽样点数N=2m，那么对于偶数序号的基2算法为

(3)

对于奇数序号的基4算法为

(4)

(5)

式(3)～式(5)组成了分裂基算法中的L型算法结构。该算法是快速傅里叶变换算法中公认最好的，具有最少的乘法和加法次数。

2 舰载发射动力学建模

2.1 修正的Craig-Bampton

结构动力学中传统的Craig-Bampton(简称C-B)方法是基于弹性体没有大范围刚体运动的假设，分析的是线性动力学问题。子结构装配时，嵌入到C-B约束模态中包含六个刚体自由度，并且约束模态的本质是静力缩聚情况下计算出的模态，其模态和频率不能相互对应。而在多体系统动力学中，已经定义了构件的刚体位移，同时构件在惯性坐标系中有大范围运动，属于非线性动力学问题，因此必须对传统Craig-Bampton子结构法进行适当修正，使其能满足多体系统动力学计算的需要。

易知，在C-B模态坐标下，子结构的结构动力学方程为

(6)

式中:Mi,Ci,Ki、Ri分别为C-B模态基下的子结构质量，阻尼，刚度和外力矩阵。

求解式(6)所对应无阻尼振动方程的特征值和特征向量：

(7)

(8)

因此，子结构的物理自由度可以表示为

(9)

利用上述正交转换修正后，使得对界面坐标依次固定时产生的模态，被无约束的模态近似代替；约束模态被边界特征向量所取代。因此，可以除去零频率对应的六个刚体运动模态，并且所有模态和频率能相互对应。

2.2 多体系统刚柔耦合动力学方程

如果物体坐标系的位置,使用它在惯性参考系中的笛卡尔坐标X=(x,y,z)T和反映刚体方位的欧拉角ψ=(ψ,θ,φ)T来表示，并且模态坐标用式q=(q1,…,qM)T表示(M为模态坐标数)，那么柔性体的广义坐标可以表示为ξ=(X,ψ,q)T。

运用拉格朗日方程可以建立柔性体的运动微分方程：

(10)

式中:K和D分别为模态刚度矩阵和模态阻尼矩阵；Kξ和Dξ分别为物体内部由于弹性变形和阻尼引起的广义力；fg为广义重力；λ对应于约束的拉格朗日乘子；Q为对应于外力的广义力。

将柔性体的计算结果和多刚体理论方法相结合可以进一步得到多体系统的刚柔耦合动力学方程。通过文献[5-6]可以推导出使用拉格朗日乘子得到的第i个柔体或刚体的方程形式为：

(11)

式中:K为动能的表达式，Qi为广义力，包括单元弹性变形和外加载荷(包括单元间载荷)引起的广义力。将式(11)与约束方程C(q,t)=0联立，即构成刚柔耦合多体动力学方程。

2.3 舰载导弹刚柔耦合动力学模型

根据舰载发射动力学知识及武器系统的子部件功能关系，对整个舰船模型进行合理处理，简化后的模型主要分为舰体和垂直发射装置。其中，垂直发射装置主要由弹库、发射筒、导弹和导轨组成：导弹和导轨间隙装配，利用闭锁机构定位；导轨通过螺栓固定于发射筒中；弹库垂直内置于舰体中，其上下端部与舰体焊接。

舰载导弹垂直发射时的力学环境非常复杂，为了描述武器系统发射时的动力学特性，特作如下假设：除了导轨和导弹，其他结构件均视为刚体，不考虑其柔性；忽略螺栓固定和焊接处的柔性效应；不考虑发射过程中导弹的变质量特性；实际中导弹与舰体质量相差悬殊，忽略导弹运动对舰体产生的影响。

由实际工程经验可知，导弹在内弹道过程中，其本身的柔性效应和导轨的变形会对出筒姿态产生严重的影响，因此需要利用相关技术手段对导弹(包括弹体和定向钮)和导轨进行柔性体建模：Adams/Flex是采用修正的Craig-Bampton法来描述弹性体的变形，同时它给Adams和Ansys提供了双向数据交换接口。对于复杂结构件，可以先利用有限元软件Ansys对构件实体模型进行网格划分，定义好附着点(施加力与约束副的外部节点)和构件实际连接处节点的关系，然后通过Adams connection命令得到模态中性文件(MNF)，再将模态中性文件导入Adams便能生成所需的柔性体，提高仿真的精确度。本文最后生成的柔性体共有64个附着点和802 324个节点数。图1为使用Ansys软件生成的柔性体中导轨的有限元模型，其材料特性密度为2.7×103kg/m3，弹性模量为70 GPa，泊松比为0.3。

图1 导轨有限元模型

由于导弹发射采用冷发射方式，发射过程中导弹所受主要激励为弹射力、闭锁挡弹器的闭锁力以及导弹定向钮与导轨的接触碰撞力。其中闭锁力的效果利用Adams中的传感器sensor激发，当弹射力大于闭锁力时开始让导弹解锁运动。

模型中的导弹和导轨为柔性体，发射过程中定向钮和导轨的接触力用Contact(Flex body to flex)工具定义，其本质为：接触碰撞采用等效弹簧阻尼模型，即弹簧接触力根据Hertz接触理论计算，同时用阻尼器模拟接触过程中的能量损失；间隙处的切向摩擦力采用coulomb摩擦模型计算。Contact工具中的具体参数值与接触材料有关，定向钮和导轨的材料分别为钢和铝，可根据试验数据和软件提供的经验数据设定：接触刚度为3.8×104N/mm；阻尼系数为28 N·s/mm；力贡献指数为1.5；最大穿透深度0.1 mm；静摩擦系数为0.3；动摩擦系数为0.1。

弹射力由提拉杆式弹射装置提供，采用随体单向力模拟该载荷，作用点位于提弹梁质心，方向近似平行于导轨，载荷大小为：

F(t)=P(t)·S

(12)

式中：P(t)为试验测得各时刻燃气压强；S为活塞筒截面积。采用AKISPL函数拟合，得到弹射力曲线。

海面上的舰艇由于海浪的波动性，会产生6自由度的摇荡运动，包括3个沿坐标轴方向的往复平移运动和3个绕坐标轴的往复旋转运动。根据对发射精度的影响程度大小，一般仅考虑横摇、纵摇和垂荡3自由度方向上的运动，认为是幅值服从瑞利分布的简谐振动的叠加[7]。利用Adams中的多自由度点驱动工具(Point Motion)可以用来模拟舰艇在5级海况中的运动：横摇周期为8 s，幅值为12°；纵摇周期为5 s，幅值为2.5°；垂荡周期为5 s，幅值为1.9 m。

最后根据子部件真实运动关系对各部分连接施加相应约束，就搭建完成整个系统刚柔耦合模型,主要部分具体拓扑连接如图2示。

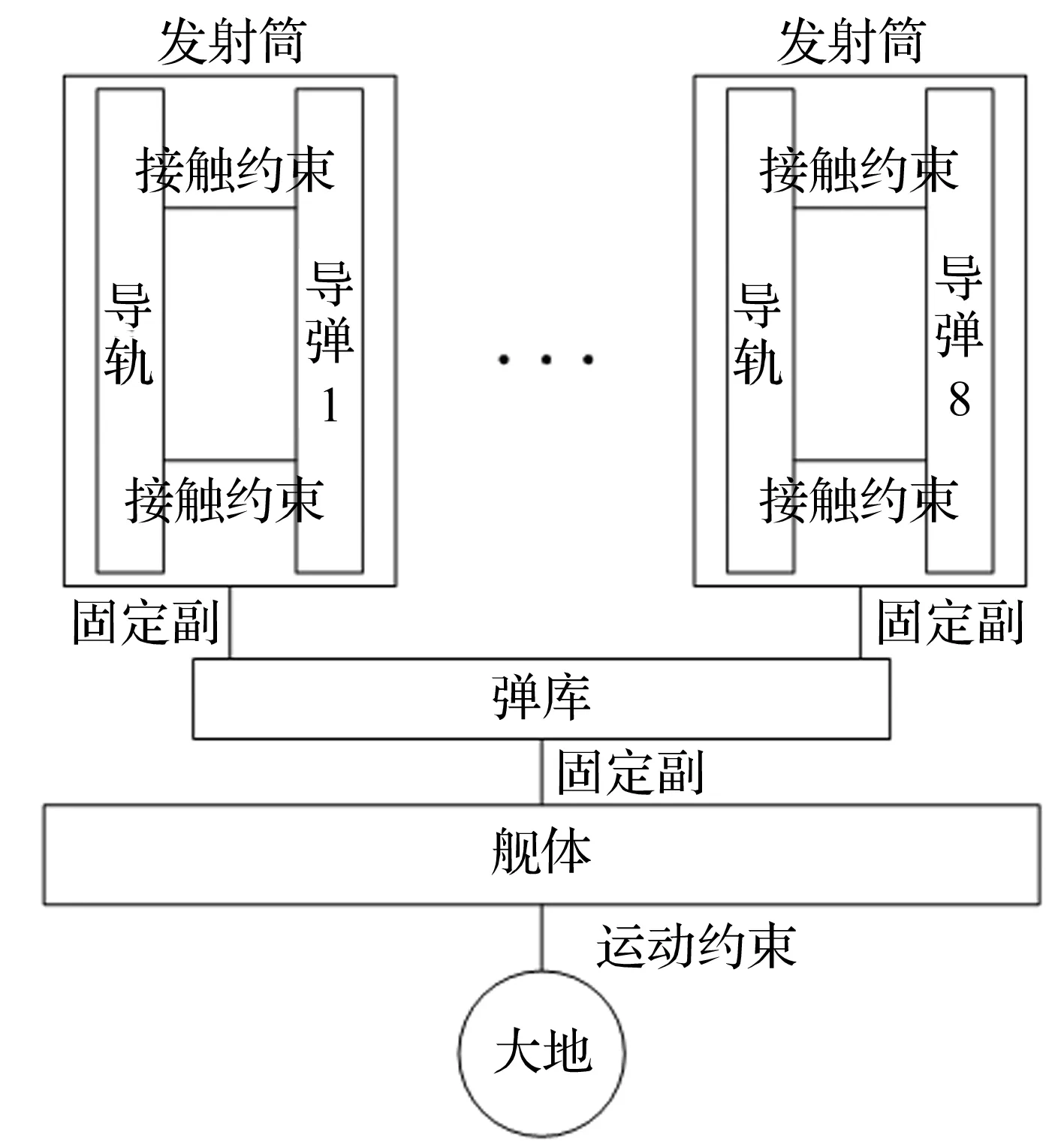
图2 拓扑连接

为了便于说明具体弹位，采用x-y格式进行描述(x表示弹库编号，y代表导弹编号)。对弹库以及导弹编号如图3所示。

图3 弹库和导弹编号

2.4 参数化自动仿真及结果分析

为了找出恶劣发射弹位，需要获取所有弹位在不同发射时刻下的导弹姿态，由于舰船弹库分布的对称性，本模型仅研究四个弹库(1,3,5,7)。考虑到工况众多(选择最小运动周期40 s，采样点间隔0.25 s，所有工况总和640种)，因此利用参数化设计，通过编译C++程序自动修改脚本文件的发射时间和发射弹位来实现自动仿真，其仿真控制流程如图4示。

图4 仿真控制流程图

仿真完成所有工况后，对保存的数据结果进行统计，列出各个弹库的角速度峰值对应弹位情况如表1所示。

表1 出筒角速度峰值

取5级海况下1-1和7-8位置对应的各六发试验弹相应数据，用以验证原模型仿真结果。1-1位置对应的导弹俯仰角速度最大为20.5 deg/s，偏航角速度最大为10.4 deg/s，滚转角速度最大为10.1 deg/s；7-8位置对应的导弹俯仰角速度最大为10.3 deg/s，偏航角速度最大为22.5 deg/s，滚转角速度最大为12.7 deg/s。与表1数值仿真结果相比，最大值在量级上基本一致，且误差在4%～10%之间，主要是由于动力学模型和海浪运动的简化处理造成。根据工程应用精度要求，文中提出的动力学仿真方法适用于工程计算和分析，计算结果是可信的。

3 发射弹位影响分析

使用数学软件工具对表1所列各恶劣弹位动力学响应信号进行频谱分析，限于篇幅所限，图5仅显示7-8弹位导弹的俯仰，偏航和滚转各姿态的频域信号图。

其中，俯仰姿态频谱图在频率为0.2 Hz时出现主峰值，远远高于其他峰值；偏航姿态频谱图则在频率为0.125 Hz时出现主峰值；而滚转姿态频谱图则包含多个大小相近的峰值。

由力学知识可知，影响导弹姿态的主要因素有以下三点：导弹的重力作用，海浪使舰船产生的摇摆运动和发射装置的结构特征引起的导弹滑块和导轨的相互碰撞力作用。通过动力学频谱分析可以方便的看出各因素的影响程度。

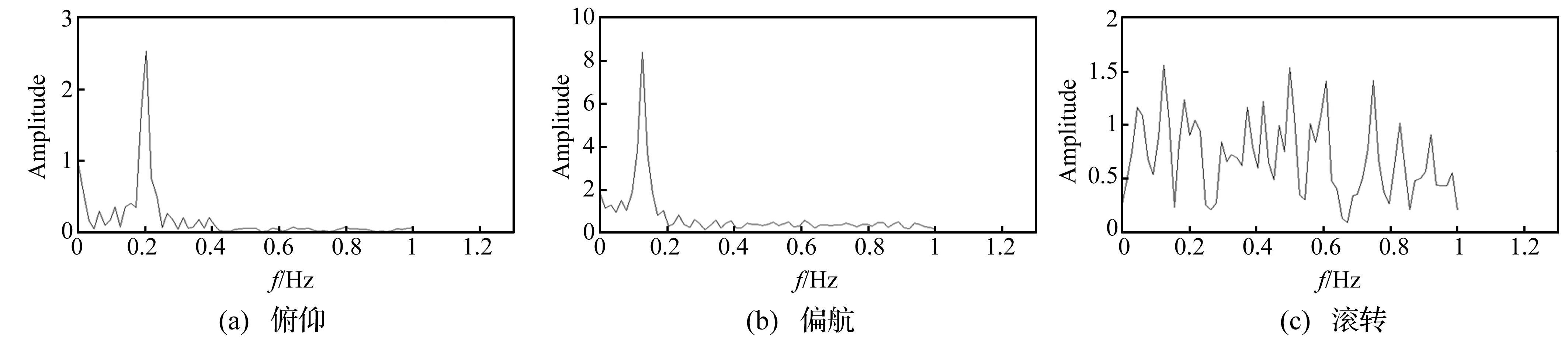
图5 角速度频谱图

从频率值来看，俯仰和偏航的频谱分析中的主峰值对应的频率在数值上正好等于舰船的纵摇和横摇频率大小，这是由于船艉5，7号弹库中导弹的俯仰方向与舰船纵摇的方向相同，偏航方向与舰船的横摇方向相同，船艏1，3号弹库中导弹的情况则恰好相反。从幅值上看，俯仰和偏航频谱分析中的直流分量主要是由重力引起的，其它峰值对应的是弹体与导轨的碰撞力，它们的大小相对于因为舰船摇摆运动而产生的主峰值小很多。因此高海情下导弹的偏航和俯仰姿态主要由舰船对应的摇摆运动引起的，而对于滚转姿态来说，其值受到三个因素的综合影响。

明确了导弹姿态和舰船摇摆运动的关系后就能详细的分析发射弹位对发射精度的影响。比较表1中四个弹库里恶劣发射弹位可知，7-8弹位的角速度模值最大。这是由于相比于5-8弹位，其离横轴较远，因而振动幅度更大，发射环境更恶劣，造成发射精度更低；相比于1-1弹位，虽然其离横轴较近，但是离纵轴较远，同时船体绕纵轴的横摇运动幅值12o比绕横轴的纵摇运动幅值2.5°高了一个数量级，因此发射精度相比起来仍然较低。

4 结 论

(1) 利用Matlab可以稳定有效的进行快速傅里叶变化，过程简单，适用于工程技术人员在一般情况下进行频域处理。基于多柔体动力学理论，在虚拟样机平台上建立的发射动力学模型是精确和高效的，更接近于真实的武器系统。

(2) 对动力学响应进行频谱分析，可以快速找出现象的本质，揭示出内在的规律，为今后类似问题的分析提供有价值的参考。

(3) 高海情下发射弹位对发射精度的影响，与舰船的摇摆运动有着密切的关系，主要取决于发射弹位距舰船横纵两轴的距离和舰船摇摆运动的幅值两个方面：距离越远则发射精度越低；如果距离一远一近，发射精度则需要考虑舰船对应摇动的幅值大小,进行综合确定。建议舰艇总体设计时，应该使弹库分布尽量靠近摇摆中心；同时，尽量避免发射弹位离横纵轴均远的导弹。

[1] 段齐骏,邱亚锋,张福祥. 舰载武器装备发射精度与载体运动关系研究[J].弹道学报,2000,12(2):60-64.

DUAN Qi-jun, QIU Ya-feng, ZHANG Fu-xiang. Study about the relationship between ship sway and launching precision of weapons[J]. Journal of Ballistics, 2000,12(2):60-64.

[2] 陈德民,槐创锋,张克涛. 精通ADAMS虚拟样机技术[M].北京: 化学工业出版社,2010.

[3] 刘益成,穆群英,赵培根. FFT算法运算次数的差分方程求解研究[J].长江大学学报(自然科学版),2008,5(3):1-3.

LIU Yi-cheng, MU Qun-ying, ZHAO Pei-gen. The method of solving number of operations for FFT algorithm by differential equation[J]. Journal of Yangtze University(Natural Science Edition), 2008,5(3):1-3.

[4] 高西全,丁玉美,阔永红. 数字信号处理-原理、实现及应用[M].北京: 电子工业出版社,2006.

[5] Orlandea N, Chance M A, Calahan D A. A sparsity-oriented approach to the dynamics analysis and design of mechanical system part[J]. Journal of Engineering for Industry, 1977, 99(3): 773-784.

[6] 洪嘉振. 多体系统动力学-理论、计算方法和应用[M]. 上海: 上海交通大学出版社,2006.

[7] 姚昌仁,唐国良,宋廷伦,等. 火箭导弹发射动力学[M].北京:北京理工大学出版社,1996.