偏斜非高斯随机振动信号幅值概率密度函数研究

程红伟，陶俊勇，陈 循，蒋 瑜

(1.国防科技大学 装备综合保障技术重点实验室，长沙 410073；2.国防科技大学 机电工程与自动化学院，长沙 410073)

工程实际中，一般基于高斯假设对随机振动信号进行统计分析和处理。然而越来越多的研究发现非高斯振动信号在实际环境中广泛存在[1-4]，忽略振动信号的非高斯性往往会导致过大的计算偏差甚至错误的结果。Steinwolf等[5]研究了湍流边界层在机翼蒙皮所引起振动的非高斯性。叶继红等[6]研究了大跨屋盖脉动风压的非高斯特性。Rouillard[7-8]分析了车辆振动环境的非高斯性，并提出了一种基于迭代算法的高斯分解方法。Rychlik等[9-11]对海浪及其引起的振动载荷的非高斯性进行了大量的统计研究。但非高斯振动信号的概率分布函数尚需要进一步研究。

对于一个平稳非高斯振动信号，概率密度函数(PDF)能够全面反映其统计特性，并决定了非高斯信号的分布规律、各阶统计矩和累积量。根据PDF曲线的对称性可以将非高斯振动信号分为对称非高斯信号和偏斜非高斯信号。对称非高斯信号的奇数阶中心矩为零，偏斜非高斯信号的奇数阶中心矩不为零。这两种非高斯信号广泛存在于实际环境中，其中对称非高斯振动信号多见于车辆结构，偏斜非高斯信号多见于风压或波浪引起的结构振动。对称非高斯信号是偏斜非高斯信号的一种特例。本文主要对典型偏斜非高斯振动信号的概率密度函数进行研究。非高斯随机过程幅值概率密度函数的数学表述方法主要有Edgeworth展开法、高斯变换法和最大熵法。Harremoäs[12]对比分析了最大熵法和Edgeworth展开法的优缺点。Winterstein[13]指出了Edgeworth展开法存在的问题，并基于Hermite多项式展开理论提出了Winterstein变换模型。当随机信号非高斯性较强时，Edgeworth展开法得到的概率密度曲线会出现负值并呈现多峰态；采用最大熵理论的方法同样会出现多峰值问题[12]。Winterstein模型计算过程比较复杂[13]。另外，Steinwolf[14]提出了一种基于经验信息的高斯曲线拼接法，该方法适用于对称非高斯信号。

综上所述，针对偏斜非高斯振动信号的幅值概率密度函数，需要提出一种既能满足计算精度要求，又相对简单的数学模型。本文基于高斯混合模型，提出了一种适用于偏斜非高斯振动信号幅值概率密度函数的数学模型。应用该数学模型对仿真非高斯振动信号和实测非高斯振动信号的幅值概率密度进行描述，通过与经验分布曲线和其他方法进行对比分析，验证了该方法的有效性和较高的计算精度。

1 非高斯统计量

理论上讲，能全面描述随机过程非高斯特性的统计量为高阶矩Mn(τ1,…,τn-1)或高阶累积量Cn(τ1,…,τn-1)[15]。但无论是高阶矩还是高阶累积量，都是时间间隔变量τi的多元函数，其估计、表述和应用都十分复杂，许多环节都可能引入较大的计算误差。高阶统计量的复杂性使其在非高斯振动的定量分析中应用较少，而主要应用于定性分析和特征识别中。通常用静态三阶和四阶统计量来描述平稳随机过程的非高斯性，即偏斜度γ3和峭度γ4[3,16]，

(1)

(2)

式中，X为非高斯随机过程；μX和σX分别为X的均值和标准差；M3和M4分别为X的3阶和4阶中心矩，可由X的概率密度函数得到。高斯随机变量的偏斜度γ3= 0，峭度γ4=3。

对于零均值平稳非高斯振动，通过时域样本序列可以对其偏斜度和峭度进行估计

(3)

(4)

式中x(t)为随机过程X(t)的样本序列；T为样本的时间长度。由于忽略了随机信号的时间相关性和四阶以上的高阶统计量，偏度和峭度不能完全表示随机振动信号的非高斯性。但在工程中，一般考虑偏度和峭度的计算结果能够满足精度要求。

2 非高斯随机振动的高斯混合模型

2.1 高斯混合模型

Middleton[17]在研究通信系统多源叠加噪声信号的幅值概率分布时提出了高斯混合模型，并在通信领域得到广泛的应用。高斯混合模型的统一表达式为

(5)

其中fNG为非高斯概率密度函数；fi(x)为第i个高斯分量的概率密度函数；αi为第i个高斯分量的权值，0 ≤αi≤ 1，∑αi=1。一般情况下，二阶或三阶高斯混合模型就可以给出精度足够高的结果。在本研究中，我们采用二阶高斯混合模型

fNG(x)=αf1(x)+(1-α)f2(x)

(6)

2.2 高阶矩分解

由于均值对概率分布的影响可以通过坐标轴平移变换得到，因此本研究基于零均值假设展开。对于零均值偏斜非高斯过程，假设其高斯混合模型为：

(7)

式中α，m1和σ1分别为高斯分量1的权重因子、均值和标准差；1-α，m2和σ2分别为高斯分量2的权重因子、均值和标准差。均值参数m1和m2的引入使高斯混合模型可以拟合偏斜概率密度曲线。式(7)中有5个未知参数，m1，m2，σ1，σ2和α。对于零均值非高斯过程其中心矩等于原点矩，以下统称为矩。非高斯随机过程的一阶矩为零，如式(8)

(8)

非高斯过程的二阶矩为方差，如式(9)

(9)

式中Ψ1(x)和Ψ2(x)分别为高斯分量1和高斯分量2的均方值，是均值和方差的函数：

(10)

将式(10)代入式(9)，非高斯随机过程的二阶矩可以展开为

(11)

同理，非高斯过程的三阶矩为

(12)

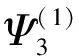
(13)

代入式(12)，非高斯随机过程的三阶矩为

(14)

类似地，非高斯随机过程的四阶矩和五阶矩如式(15)和(16)所示

(15)

(16)

对于式(15)，有

(17)

将式(17)代入式(15)，则非高斯随机过程的四阶矩为

(18)

对于式(16)，有：

将式(19)代入式(16)，则非高斯随机过程的五阶矩为

(20)

实际问题中，非高斯随机过程的各阶矩是未知的，一般根据样本记录得到其估计值。假设零均值非高斯过程的时间样本序列为x(t)，则其第i阶矩的估计值为

(21)

用估计值代替各阶矩的理论值，联立式(8)、(11)、(14)、(18)和(20)，得到关于未知参数α,m1,m2,σ1,σ2的五元方程组：

(22)

3 仿真算例与试验

为综合验证所提出的高斯混合模型的有效性，分别给出了以下两个示例：① 基于非线性变换得到的仿真加速度振动信号；② 非高斯振动台悬臂梁振动试验测量得到的非高斯应力响应信号。两种信号均为各态历经随机过程。

3.1 仿真信号

首先生成图1所示的零均值高斯信号，信号的标准差σx= 74.85 ms-2，功率谱(PSD)如图1(b)所示。对图1(a)所示的高斯信号进行如下非线性变换并去除均值，得到零均值非高斯信号z0(t)，如式(23)所示：

z(t)=x(t)+0.002x2(t)

z0(t)=z(t)-mean(z)

(23)

式中:z0(t)的时间序列及功率谱如图2(a)和图2(b)所示。z0(t)的标准差σz0= 76.78 ms-2，偏度γ3= 0.915 0，峭度γ4= 4.196 9。

将非高斯时间序列代z0(t)入式(21)，得到各阶矩的估计值：

将上述估计结果代入式(22)，得高斯混合模型各参数的估计估计结果

图1 仿真高斯随机振动信号

图2 仿真非高斯随机振动信号

将上述结果代入式(7)，得到图2(a)所示非高斯时间序列的幅值概率密度函数：

(24)

基于式(24)得到的非高斯概率密度曲线如图3所示。图3中同时给出了基于Edgeworth方法、Winterstein模型的概率密度曲线以及基于样本序列的经验分布曲线。图3(a)为线性坐标，可以清晰地显示分布曲线中间峰值部分的差异；图3(b)为半对数坐标，可以清晰地显示分布曲线在尾部的差异。通过对比分析，高斯混合模型和Winterstein模型得到的结果比较理想，Edgeworth方法计算的概率密度曲线偏离经验分布比较明显，而且曲线出现局部起伏，对于偏度和峭度更大的非高斯信号，这些起伏会继续发展，导致出现多峰值甚至负值。

为进一步分析和比较各种方法的准确性，这里以相对均方误差来衡量各幅值概率密度曲线对经验分布曲线的偏离程度。相对均方误差定义为

(25)

式中f为基于某种方法得到的非高斯概率密度函数，fEM为基于样本序列的经验分布。则图3中，对应于Edgeworth展开的均方误差rEdge= 2.13%，Winterstein模型的均方误差rWinter= 1.43%，高斯混合模型的均方误差rGM= 1.03%。综合图3和均方误差结果，可以看出高斯混合模型能够给出图2所示仿真非高斯信号最准确的概率密度函数解析表达式。

3.2 实测信号

如图4所示的悬臂梁结构，其材料为铝合金2024-T3。悬臂梁的几何尺寸见图4，悬臂梁根部通过夹具固定在振动台上构成如图所示的基础激励振动系统。基础激励的输入信号是加速信号，如图5所示。输入加速度为对称非高斯信号，偏度γ3= 0，峭度γ4= 6，标准差σ= 10 g(g表示重力加速度)。振动试验是在竖直方向上进行的，由于重力和其他非线性因素的影响，图4所示的悬臂梁根部的应力响应为偏斜非高斯过程，去除均值以后的应力信号如图6所示，信号标准差σ=41 MPa，偏度γ3=-0.7102，峭度γ4=4.7977。将图6所示的非高斯应力响应序列代入式(21)得到各阶矩的估计值：

将上述结果代入式(22)，得到高斯混合模型各个参数的估计结果

图3 仿真非高斯信号幅值概率密度曲线

图4 悬臂梁结构基础激励振动试验(单位：mm)

图5 非高斯振动试验输入信号

图6 非高斯振动试验的应力响应

将上述结果代入式(7)，得到图6(a)所示非高斯振动信号的幅值概率密度函数：

(26)

图7中分别给出了基于高斯混合模型、Edgeworth展开法和Winterstein模型的概率密度曲线以及基于样本序列的经验分布曲线。根据式(26)Edgeworth展开法相对于经验分布的均方误差为rEdge=1.39%；Winterstein模型的均方误差为rWinter=0.91%，高斯混合模型的均方误差为rGM= 0.30%。通过图7的分析和均方误差的定量比较发现，对于图6所示的实测非高斯应力信号，基于高斯混合模型能够给出其概率密度曲线的最优解析表达式。

对于工程中的偏斜非高斯振动信号，其偏度，-1.2<γ3<1.2。示例3.1中仿真信号的偏度为0.915 0，示例3.2中实测信号的偏度为-0.710 2。二者分别接近常见非高斯信号偏度的上限和下限。总结示例的分析结果，可以得出结论：基于高斯混合模型的数学表达式能够准确地表示偏斜非高斯信号的幅值概率密度。

图7 实测非高斯振动应力信号幅值概率密度曲线

4 结 论

基于高斯混合模型，利用高斯随机变量高阶中心矩和原点矩之间的关系，提出了一种求解偏斜非高斯振动幅值概率密度函数的方法。该方法的数学模型简单，能够准确表示偏斜非高斯振动信的概率密度。

通过仿真和实测非高斯振动信号验证了所提出方法的有效性和工程适用性。

本文提出的基于高斯混合模型的概率密度函数模型为偏斜非高斯振动信号的相关研究研究(如疲劳分析，减振隔振等)提供了准确的统计分析工具和重要的理论支撑。

[1] Benasciutti D，Tovo R.Fatigue life assessment in non-Gaussian random loadings [J].International Journal of Fatigue，2006，28(7): 733-746.

[2] 王旭，黄鹏，顾明.海边坡角可调试验房风载荷现场实测研究[J].振动与冲击，2012，31(5): 176-182.

WANG Xu，HUANG Peng，GU Ming.Field investigation on wind loads of a low building with adjustable roof pitch near see [J].Journal of Vibration and Shock，2012，31(5): 176-182.

[3] 何军.非高斯载荷作用下结构首次失效时间分析的Monte-Carlo模拟方法[J].振动与冲击，2007，26(3): 59-60.

HE Jun.Monte-Carlo simulation for first failure time of structures excited by non-Gaussian load [J].Journal of Vibration and Shock，2007，26(3): 59-60.

[4] Aberg S，Podgórski K，Rycklik I.Fatigue damage assessment for a spectral model of non-Gaussian random loads [J].Probabilistic Engineering Mechanics，2009，24(4): 608-617.

[5] Steinwolf A，RizziS A.Non-Gaussian analysis of turbulent boundary layer fluctuating pressure on aircraft skin panels [J].Journal of Aircraft，2006，43(6): 1662-1675.

[6] 叶继红，侯信真.大跨屋盖脉动风压得非高斯特性研究[J].振动与冲击，2010，29(7): 9-15.

YE Ji-hong，HOU Xin-zhen.Non-Gaussian features of fluctuating wind pressures on long span roofs [J].Journal of Vibration and Shock，2010，29(7): 9-15.

[7] Rouillard V.The synthesis of road vehicle vibrations based on the statistical distribution of segment lengths [C]//ACAM.Proceedings of 5th Australasian Congress on Applied Mechanics.Brisbane，Australia: ACAM，2007:1-6.

[8] Rouillard V.On the non-Gaussian nature of random vehicle vibrations [C]// WCE 2007.Proceedings of the World Congress on Engineering 2007.London，UK: WCE，2007.1219-1224.

[9] Rychlik I，Johannesson P，Leadbetter M R.Modeling and statistical analysis of ocean-wave data using transformed Gaussian processes [J].Marine Structures，1997，10(1): 13-47.

[10] Podgórski K，Rychlik I，Machado U B.Exact distributions for apparent waves in irregular seas [J].Ocean Engineering，2000，27(9): 979-1016.[11] Butler R W，Machado U B，Rychlik I.Distribution of wave crests in a non-Gaussian sea [J].Applied Ocean Research，2009，31(1): 57-64.

[12] Harremo⊇s P.Maximum entropy and the Edgeworth expansion [C]// IEEE.Proceedings of the IEEE Information theory workshop.Awaji Island，Japan: IEEE，2005.68-71.

[13] Winterstein S R.Nonlinear vibration models for extremes and fatigue [J].Journal of Engineering Mechanics，1988,114(10): 1772-1790.

[14] Steinwolf A.Approximation and simulation of probability distributions with a variable kurtosis value [J] Computational Statistics & Data Analysis，1996，21(2): 163-180.

[15] Mendel J M.Tutorial on higher-order statistics (spectra) in signal processing and system theory: theoretical results and some applications [J].Proceedings of the IEEE，1991，79 (3): 278-305.

[16] 蒋瑜，陶俊勇，王得志,等.一种新的非高斯随机振动数值模拟方法[J].振动与冲击，2012，31(9): 169-173.

JIANG Yu，TAO Jun-yong，WANG De-zhi，et al.A novel approach for numerical simulation of a non-Gaussian random vibration [J].Journal of Vibration and Shock，2012，31(9): 169-173.

[17] Middleton D.Non-Gaussian noise models in signal processing for telecommunications: new methods and results for class A and class B noise models [J].IEEE Transactions on Information Theory，1999，45(4): 1129-1149.