一种五自由度机械手直线轨迹规划方法研究

，，

(1.华中科技大学船舶与海洋工程学院，湖北 武汉 430074；2.空军预警学院，湖北 武汉 430010)

一种五自由度机械手直线轨迹规划方法研究

刘通1，唐国元1，黄道敏2

(1.华中科技大学船舶与海洋工程学院，湖北 武汉 430074；2.空军预警学院，湖北 武汉 430010)

针对一种有特定作业要求的五自由度机械手进行了轨迹规划研究。在运动学模型和工作空间的基础上，根据机械手末端的直线运动需求，不失一般性，设定所研究机械手的末端直线轨迹，分析了相应的轨迹规划的约束条件并建立约束方程。得到了在轨迹生成过程中各关节角和末端执行器作业中心的对应关系。详细分析了2种轨迹规划的算法，即多项式线性插值法和有界偏差关节路径法(BDJP)。并用这2种方法对机械手末端作业所需要的直线轨迹进行了仿真，给出仿真结果。

机械手；工作空间；直线轨迹规划；有界偏差关节路径法

0 引言

机械手的轨迹，指操作臂在机械手运动过程中的位移、速度和加速度。轨迹规划是根据作业任务的要求，计算预期的运动轨迹[1]，也就是求出每个关节的关节角度随时间的变化函数。因此，针对一种有特殊作业要求的五自由度机械手，进行了三维空间的连续直线轨迹规划研究。机械手须满足对作业目标实现直线插拔或者旋进旋出动作，机械手末端执行器的姿态在运动过程中保持不变。连续直线轨迹规划，是在末端执行器保持姿态的情况下要求机械手末端执行器时刻按照预定直线轨迹匀速运动。在计算得出的工作空间的基础上，详细研究了末端执行器沿直线轨迹运动过程中各个关节角随时间的变化函数。分别用预先解算关节变量解和实时解算关节变量2种算法对该模型进行了仿真研究。

1 机械手系统及功能

机械手具有五自由度6功能。作业动作由大臂的摆动、大臂俯仰、中臂俯仰、小臂俯仰、手腕的旋转和手爪的夹持等动作组合组成，三维模型如图1所示。

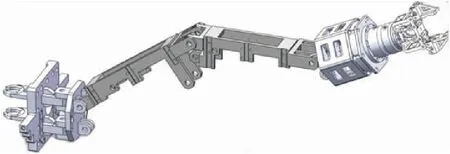
图1 机械手结构

根据实际作业要求，结合图2，对要求作出具体说明，即末端执行器须沿直线AB运动，实现插拔功能；末端执行器沿直线AB前进或者后退的速度v和腕关节旋转速度ω，须满足关系ω=tv(t是不为零的常数)，实现旋进旋出螺栓的功能；末端执行器轴线始终与AB连线方向保持一致。

图2 机械手作业路径要求

2 运动学模型及工作空间计算

利用D-H法描述机械手连杆间关系，建立运动学模型。模型关节角范围、机械手参数分别如表1和表2所示。拓扑结构如图3所示。

表1 关节角度范围 (°)

表2 机械手参数表

图3 机械手拓扑

根据各个坐标系之间的变换关系，可以得到从零坐标系到第5个坐标系的转换矩阵，即

(1)

(2)

c2=cosθ2；s2=sinθ2；c2+3+4=cos(θ2+θ3+θ4)，其他类似，下同。

式(2)就是将末端执行器的位置表示在基坐标下的结果。如果零坐标原点位置记为基坐标原点，上述4×4矩阵第4列前3行就是末端执行器在三维坐标中的位置，即

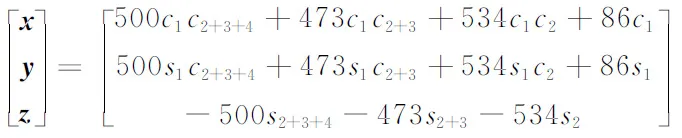
(3)

根据式(3)，可知末端执行器作业中心位置与各关节角的关系，并可利用变换矩阵和蒙特卡洛法绘制其工作空间[2]。

3 轨迹生成及仿真

3.1 轨迹生成的约束条件

(4)

由式(4)可以看出，处于第5坐标系的末端执行器的接近矢量由前4个关节角度决定。当指定了这个矢量的各个分量之间的关系，就固定了矢量的方向，即末端执行器的接近矢量。该模型中，第1个关节绕基坐标Z轴旋转变化，每一个固定值对应一个作业面，每一个作业面的范围由第2、3、4关节决定。为了简便直观，将第1个关节角即图2所示的摆动关节固定，使之处于运动学模型的零位，此时末端执行器工作面就在基坐标的X-Z平面，只需关注一个二维平面即可。

设定目标物为一直线杆件，用一个基坐标下的方向向量(1，0，-1)表示其姿态。作业要求为将杆件夹持，沿着杆件长度方向在基坐标中(1 440，0，-400)到(1 300，0，-260)的直线上运动，实现接插件的插拔，末端执行器在有姿态要求的机械手作业区域内，完成预定直线轨迹运动。

根据作业要求为式(3)添加约束条件，即

(5)

利用逆运动学，可由末端执行器位置反向推算角度空间中各关节角大小[3]。令式(3)分别等于作业起点位置[1 440 0 -400]T和终点位置[1 300 0 -260]T，再加上约束条件式(5)，合并得方程组为：

(6)

计算出在作业起点和终点的关节角度分别为：

确定了轨迹的起点到终点，接下来就要求在一定的时间内，4个角度值同时从起点值变化到终点值。最终需要求出这些关节角度的时间函数，也就确定了末端执行器作业中心的运行轨迹。假定这段路程所需时间为15 s。

3.2 轨迹规划算法

机械手轨迹规划的算法很多，插值法和有界偏差关节路径法是较常用的算法。插值法是利用有限数量的已知点构造一个有限次数的多项式来代替未知函数，再根据这个替代函数计算已知点以外的其他点的函数值。在数值计算理论中插值的方法有很多，如Lagrange插值、Newton插值和Hermite插值等[4]。其中简单有效的是Newton插值法，构造一个三次多项式来拟合几个角度的时间函数。构造三次Newton插值，至少需要4个已知点，故还须另外解出2个点。

求出θ2、θ3和θ4的时间函数分别为：

(7)

式(7)代入式(3)，利用Matlab的可视化仿真功能[5]，得到拟合结果。

有界偏差关节路径法BDJP(bound deviation joint path)是Taylor提出的一种关节空间的运动算法[6]。在轨迹规划过程中，根据直线轨迹首尾2点，依次取已知点的中间节点，直到机械手在每段运动中偏离预定轨迹的最大偏差在规定范围δmax内。该方法实质是递归两分法求中间点。

计算轨迹起点P0和终点P1关节矢量q0和q1，根据关节矢量求得中间点关节角度值为：

qm=q0+(q1-q0) /2

(8)

根据qm求得中间点Pm。而直接由起点和重点算得的中间点位置为：

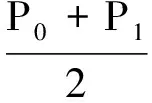
(9)

计算Pm和Pc的偏差为：

δp=|Pc-Pm|

(10)

如果δp<δmax，则停止进一步寻找中间点，采样下一段轨迹。否则计算中间点Pc的关节矢量，并以Pc代替P1，P0代替Pc，进一步寻找满足条件的中间点。其流程算法如图4所示。

图4 BDJP算法流程

3.3 仿真结果及分析

从图5可以看出，Newton插值法能很好地逼近预期的轨迹，在已知点附近，误差是很小的，误差最大的地方出现在2个已知点之间中心位置，约为2.5 mm。这个精度仍无法满足如旋动螺栓或者插拔高精度接插件等特定作业要求。此外，如果轨迹很长，就需要解出很多个中间节点，以便求出高次拟合多项式来保证精度。但是，机械手轨迹插值法的多项式次数一般不多于3次，次数大于3次的关节函数积分得到加速度不是一个常数，加速不稳定会带来机械结构的振动[7]。多次求解带来的累积误差，也会使末端执行器位置精度不能保证。

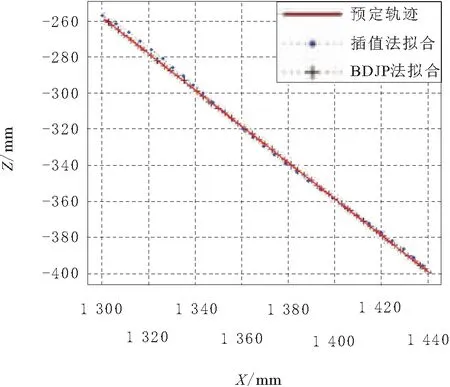
图5 插值法和BDJP法仿真结果

计算发现用BDJP法在X-Z平面跟踪预定轨迹时，X方向的偏差大于Z方向的偏差10倍以上，所以只需关注X方向的偏差Xerr。图5所示的结果是Xerr=0.5 时的结果。对比图5中的2种算法，可以发现偏差明显减小。为进一步对比2种算法误差大小，另再绘制误差对比图，如图6所示。

图6 插值法和BDJP法偏差对比

由图6可知，多项式插值的方法拟合的最大误差约为2.6；而用BDJP法最大误差为0.2，为插值法的1/13。

由分析仿真过程与结果可知，针对所研究的五自由度机械手，BDJP法有以下优点：算法收敛性好，仿真结果表明，每次递归之后的偏差减少60%以上；算法简单，容易操作；可以仿真任意轨迹；仿真过程中，误差可见而且能在算法中得以控制。

对比插值法和BDJP法，发现后者有明显优势，在精度要求方面和算法实施方面都能满足该项目实际要求。

4 结束语

以机械手运动学模型为基础，计算出工作空间，规划直线运动轨迹。并用Matlab仿真2种轨迹跟踪的算法，比较2种算法优劣，BDJP法在机械手工程实践中能很好地应用。

[1] 熊有伦.机器人技术基础[M].武汉:华中科技大学出版社，2008.

[2] 赵燕江，张永德.基于Matlab的机器人工作空间求解方法[J].机械科学与技术，2009，28(9):1658-1661.

[3] Craig J J.Introduction to robotics: mechanics and control[M].New York: Addison-Wesky Publishing Co.，1989.

[4] 李红.数值分析[M].武汉:华中科技大学出版社，2010.

[5] 周建兴，等.Matlab从入门到精通[M].北京:人民邮电大学出版社，2009.

[6] Russell H.Taylor，Planning and execution of straight line manipulator trajectories in robot motion[M].Massachusetts: The MIT，1983.

[7] Macfarlane Sonja，Croft Elizabeth A.Jerk-bounded manipulator trajectory planning: design for real-time application [J].IEEE Transactions on Robotics and Automation，2003，19(1):42-52.

Study of Linear Trajectory Planning Method for Five-freedom Robot

LIUTong1，TANGGuoyuan1，HUANGDaomin2

(1.School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China；2.Air Force Early-warning Academy of PLA，Wuhan 430010，China)

Trajectory planning for a five-DOF manipulator is studied in this paper.On the basis of the kinematic model and workspace，according to linear motion needs of manipulator ends，a straight trajectory was set to analyze constraint and constraints equations were established.The correspondence between each joint angle and end effector operations center was obtained in the trajectory generation process.Details of the two kind of trajectory planning algorithm were introduced，that is polynomial interpolation and bound deviation joint path.A straight path which is used in actual operation was simulated with the two algorithms and the result was shown.

robot； workspace； straight trajectory generation；BDJP

2014-08-18

国家科技重大专项资助项目(2011ZX05027-004-02-03)

TP241.2

A

1001-2257(2014)12-0008-04

刘通(1987-)，男，四川通江人，硕士研究生，研究方向为舰船与水下航行体运动控制，水下作业技术；唐国元(1973-)，男，湖北利川人，工学博士，硕士研究生导师，副教授，研究方向为舰船与水下航行体运动控制，舰船机电控制系统及特种装置系统，舰船动力装置智能化理论与技术；黄道敏(1971-)，女，安徽凤阳人，博士，研究方向为水下机器人，机电控制技术。