基于阿克曼定理的四轮独立转向模糊控制算法研究

，

(南京航空航天大学自动化学院，江苏 南京 210016)

基于阿克曼定理的四轮独立转向模糊控制算法研究

陈国栋，王志胜

(南京航空航天大学自动化学院，江苏 南京 210016)

基于阿克曼转向定理，研究电动汽车四轮独立转向系统。利用轮胎“魔术公式”建立二自由度非线性模型，并提出一种基于模糊策略的方法对其质心侧偏角进行控制。整车系统仿真的输入为左前轮车轮转角，其余3个车轮转角由模糊控制决定。质心侧偏角作为模糊控制器的输入，满足阿克曼定理的3个车轮转角作为其输出，由此实现四轮独立转向的控制。仿真研究结果表明所提出算法的有效性。

四轮独立转向；阿克曼定理；魔术公式；模糊控制

0 引言

目前，对四轮转向电动车的研究，一般都是研究1/2车辆模型，建立二自由度或者三自由度，线性模型或者非线性模型，围绕质心侧偏角为零的控制目标选择各种控制策略[1-2]，没有考虑阿克曼转向定理。也有考虑到阿克曼转向定理，但其建立的模型都是简单的线性模型[3-4]，利用的都是线性控制策略，没有考虑到轮胎的非线性特性。

在车辆二自由度非线性模型的基础上，同时满足阿克曼转向定理，建立了整车的四轮独立转向模型，并基于质心侧偏角利用模糊控制策略对其进行仿真，验证了模型的正确性和控制策略的有效性。

1 四轮电动独立转向数学模型

1.1 阿克曼定理

汽车在转向行驶过程中，全部车轮会绕一个瞬时中心点做圆周滚动[5]，如图1所示。图1中，δ1,δ2,δ3,δ4为4个车轮的转角；α1,α2,α3,α4为4个车轮的侧偏角；F1,F2,F3,F4为各个车轮产生的侧向力；u，v分别为车辆纵向和横向速度；β为车辆质心侧偏角；γ为整车绕质心的横摆角速度；a,b分别为质心到前后轴的距离；c为两车轮间的轴距；O为汽车转向的中心；d,e分别为转向中心到前后轴的纵向距离；f为转向中心到左后轮的横向距离。则其运动几何关系为：

(1)

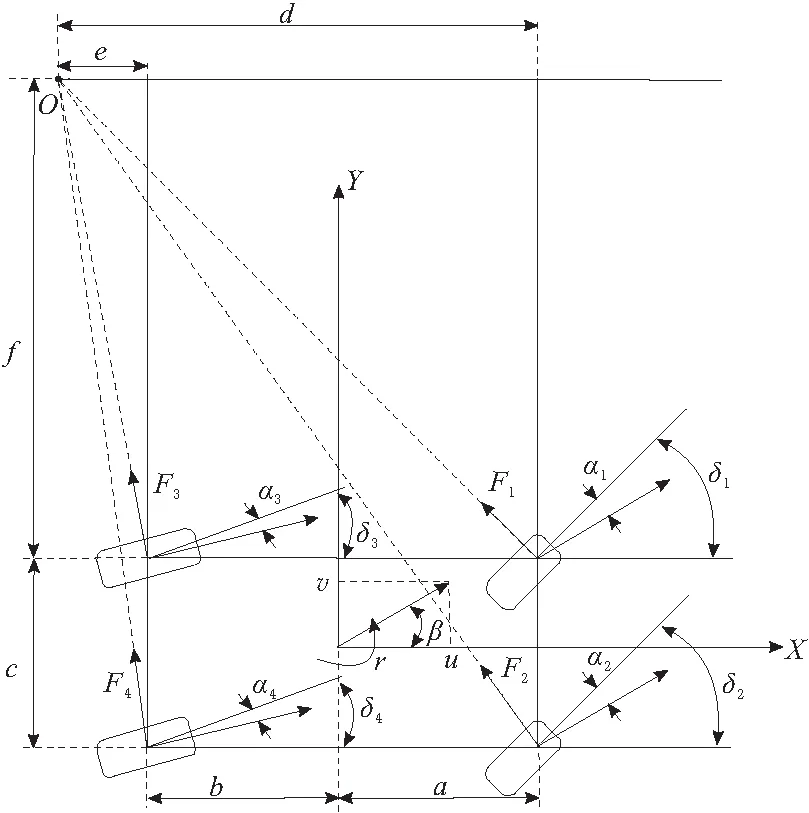
图1 整车模型

1.2 动力学建模

为分析四轮独立转向系统的各个车轮的转角和整车的稳定性能，同时为了简化系统的模型，特作如下合理的假设。

a.整车重量平均分配到4个车轮。

b.每个车轮特性一样，同时忽略车轮轮胎由于载荷变化而引起的轮胎特性变化。

c.忽略汽车悬架的作用，,即不考虑汽车垂向的位移运动，绕横向轴的俯仰运动和绕纵向轴的侧倾运动，认为车辆只是在平行与地面运动。则建立四轮独立转向二自由度非线性动力学方程为[6]:

(2)

(3)

m为整车的重量；JZ为整车转动惯量。

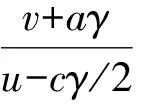
(4)

(5)

(6)

(7)

1.3 轮胎模型

传统汽车动力学建模一般采用线性轮胎模型，而轮胎线性模型的前提是在侧偏角非常小(小于5°)的情况下，而在侧偏角或者侧向加速度较大的情况下就需要轮胎的非线性模型来模拟。Pacejka模型(魔术公式)是一个半经验半理论模型，能够仿真轮胎的线性和非线性特性，同时可以描述轮胎的稳态力学[7]。轮胎侧向力方程为：

Fy=Dsin(Carctan(Bαi-E(Bαi-arctan(Bα1))))

(8)

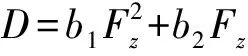
2 四轮独立转向模糊控制算法

模糊控制是一种智能的控制策略，能够模仿人的思维方式，对于非线性问题可以得到很好的解决。其设计主要过程是确定输入和输出变量的论域，模糊化，确定控制器结构选择，模糊规则制定和去模糊化。采用的是普遍采用的二维模糊控制器，其以系统的误差E和误差的导数EC作为输入变量，可以很好的反应输入变量的动态特性[8]。

论域的选择，质心侧偏角误差E的论域范围为[-6，6]；质心侧偏角误差导数论域范围为[-6，6]；左前轮和左后轮转角比U论域范围为[-1，1]。针对所研究的四轮独立转向控制系统的实际经验，质心侧偏角误差E和误差导数基本论域分别为[-0.1，0.1]和[-0.01，0.01]；左前轮和左后轮转角比U基本论域范围为[-1，1]。则量化因子和比例因子的确定如下所示，质心侧偏角误差的量化因子ke=6/0.1，误差导数的量化因子kec= 6/0.01，控制量输出的比例因子ku=1/1。E,EC和U的模糊集为{NB，NM，NS，ZO，PS，PM，PB}。如图2所示。

采用两输入一输出的控制器形式，两输入变量的语音值都为7，则总共有49条if A and B then C形式的规则，如表1所示。

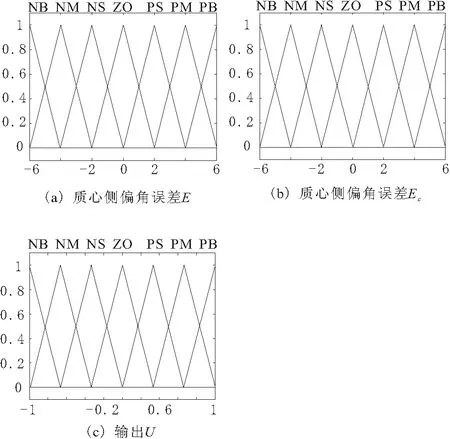
图2 输入输出的隶属度函数

表1 模糊规则

3 仿真实验与对比

整车的主要参数如表2所示。

表2 整车参数

为了验证提出的基于阿克曼转向定理四轮独立转向的非线性模型正确性及控制策略的有效性，特以传统两轮转向(2WS)模型和传统前后轮比例转向(4WS)模型[1,9]作为对比。仿真输入的车速为20m/s，左前轮转角为0.08rad/s时，车速为30m/s，左前轮转角为0.2rad/s。仿真结构如图3所示。

不同车速转角下的质心侧偏角如图4所示，线性四轮转向汽车(4WS)质心侧偏角在短时间波动后能够迅速的达到稳定值，基本没有误差。而四轮独立转向汽车(4WIS)质心侧偏角也在很短的时间内达到稳定，说明控制策略是有效的，同时由于采用非线性模型，具有不确定性，其质心侧偏角有很小的稳态误差，但在合理范围内。两轮转向汽车(2WS)的质心侧偏角较大，尤其是在高速大转角情况下。而传统四轮转向(4WS)和四轮独立转向(4WIS)在速度和转角变化下能够很好的限制质心侧偏角。

图3 整车仿真结构

图4 不同车速转角下的质心侧偏角

不同车速转角下横摆角速度如图5所示，两轮转向汽车(2WS)在高速大转向情况下横摆角速度非常大，超出合理的范围，这是由于前轮转向角度太大，而轮胎线性模型导致前轮侧向力相应变大，而后轮又理论上没有侧向力，这样导致横摆角速度超出了合理范围。而四轮转向汽车(4WS)的横摆角速度有所增加，这是由于线性轮胎模型采用，前后轮侧向力都有所增大，导致整车横摆角速度有所增大。而四轮独立转向汽车(4WIS)由于采用非线性轮胎模型，轮胎侧向力在大转角下基本不变，而轮胎的转角变大，由式(2)可知整车的横摆角速度有所下降。

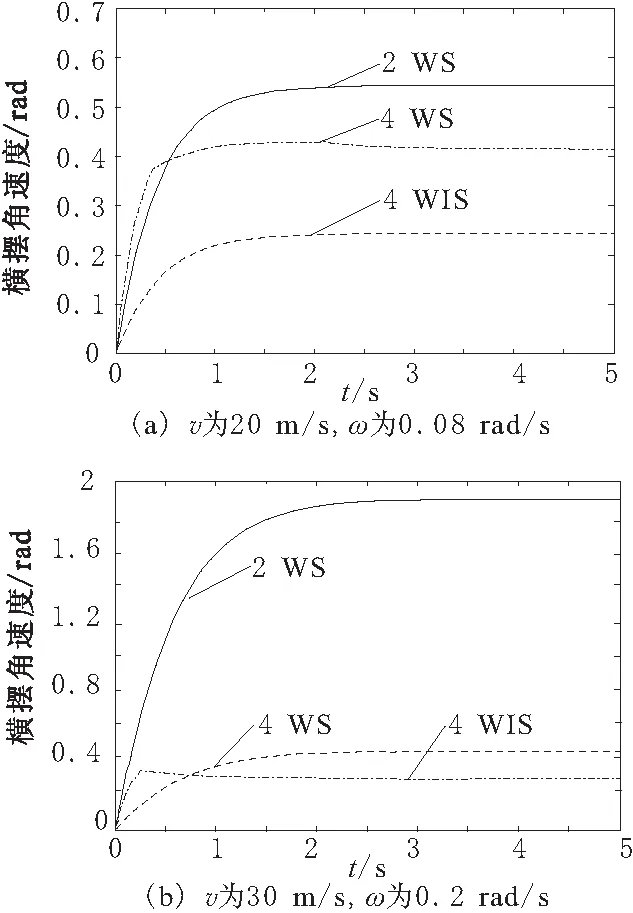
图5 不同车速转角下横摆角速度

不同车速转角下4个车轮转角如图6所示，四轮独立转向汽车(4WIS)后面的2个车轮经过一个较短的时间稳定，同时后面2个车轮转角较小而且相差不大，而前面的2个车轮在高速大转角下转角出现明显的差别。通过车轮转角看出，模糊控制策略可以在很短时间内让4个车轮转向稳定。

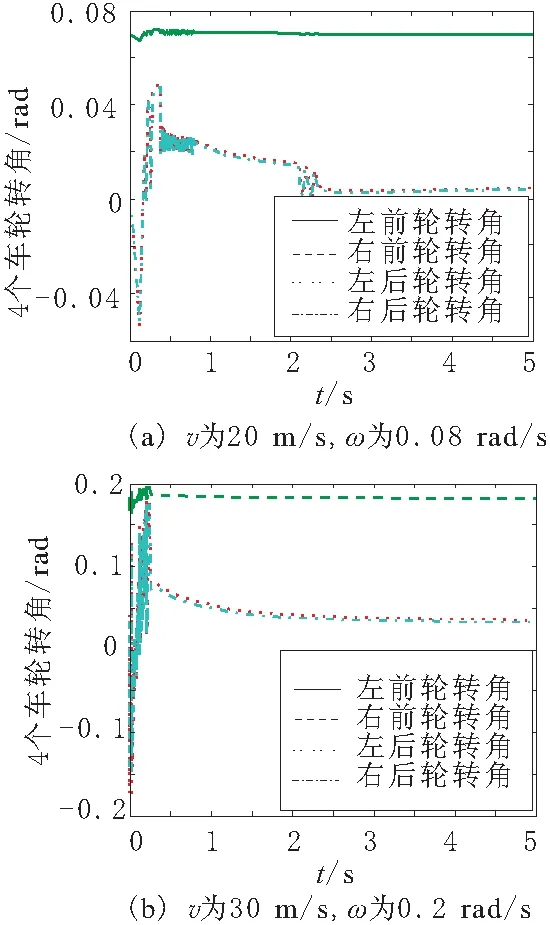
图6 不同车速转角下4个车轮转角

4 结束语

针对传统四轮转向建模过程中采用的线性模型，没有考虑转向过程中左右车轮转角的差异性，提出的基于阿克曼定理的四轮独立转向的非线性模型，采用模糊控制，通过Matlab对整车在低速小转角和高速大转角的仿真，在小转角工况下仿真出的质心侧偏角和横摆角速度跟传统四轮比例转向(4WS)接近，能够证明模型的正确性和控制策略的有效性。而在大转向工况下，四轮独立转向(4WIS)模型由于采用非线性模型，更能反映实际车辆运行状态，同时能够反映左右车轮转角的差异性，这是四轮转向(4WS)和两轮(2WS)转向所不具备的。

[1] 林程,孟祥,陈思忠,等.四轮转向车辆转向特性分析及试验研究[J].北京理工大学学报,2004,24(3):218-221.

[2] 田承伟,宗长富,何磊,等.汽车线控四轮转向控制策略[J].吉林大学学报工学版,2010,40(5):1177-1182.

[3] 舒进,陈思忠,杨林.四轮独立转向系统控制策略与试验[J].农业机械学报,2005,36(7):25-28.

[4] 冯严科,韩致信,雷继军,等.一种四轮独立转向车辆的稳态响应分析[J].科学技术与工程,2010,10(10):2380-2383.

[5] Ackermann J,Odenthal D,Bunte T.Advantages of active steering for vehicle dynamics control[C]//Proceedings of 32nd ISATA,Automotive Mechatronics Design and Engineering,1999.263-270.

[6] 杨福广.4WID/4WIS 电动车辆防滑与横摆稳定性控制研究[D].济南:山东大学,2010.

[7] Bakker E,Pacejka H B,Lidner L.A new tire model with an application in vehicle dynamics studies[J].SAE Paper ,1989.890087:101-113.

[8] 德丰.Matlab模糊系统设计[M].北京:国防工业出版社,2009.

[9] 郭孔辉,轧浩.四轮转向的控制方法的发展[J].中国机械工程,1998,9(5):73-75.

Fuzzy Control Method Based on Ackermann Steering Theorem for Four-wheel Independent Steering

CHENGuodong，WANGZhisheng

(Nanjing University of Aeronautics and Astronautics,Institute of Automation,Nanjing 210016,China)

Four-wheel independent steering system for electric vehicles is studied based on Ackermann steering theorem.A 2-DOF nonlinear steering model is established based on the tire “magic formula” model.And a new method based on fuzzy control strategy is proposed for its sideslip angle control.The left front wheel angle is input to the simulation of vehicle System,and the remaining angles of three wheels are decided by the fuzzy control.The sideslip angle is input to the fuzzy controller and the remaining angles of three wheels which meet Ackerman theorem are output to control four-wheel independent steering.And its control effect is compared with the traditional front-wheel steering and the traditional four-wheel proportional steering.Simulation results indicate that the new algorithm in this paper is effective .

four-wheel independent steering;Ackermann steering theorem;magic formula;fuzzy control

2014-04-15

U469.72

A

1001-2257(2014)08-0026-04

陈国栋(1989-)，男，江苏宝应人，硕士研究生，研究方向为电动汽车建模与仿真;王志胜(1970-)，男，湖北松滋人，教授，博士研究生导师，研究方向为机电模拟技术、工业机器人技术。