基于eM-Plant的医用轨道物流传输系统仿真与优化

2014-09-06臧铁钢王静静

机械设计与制造工程 2014年1期

张中，臧铁钢，王静静

(南京航空航天大学机电学院，江苏南京 210016)

轨道物流传输系统(简称TVS)是一种在医院中被广泛使用的先进物流传输方式，它是在计算机控制下，利用智能轨道载物小车在专用轨道上传输物品的系统［1］。当前，在医用TVS系统设计的过程中，供应厂商处于主导地位，大部分设计方案都由其完成。有不少医院已经建成很长时间后才引入该系统，而原先科室设计并非最优布局，或者在建成规划初期并不清楚每个科室的预计物流量，导致原有科室布局无法使TVS系统运行效率达到最佳。而有时供应厂商依靠传统设计经验，并未对医院具体现状进行考察、研究和系统分析，同样使得建造效果未达到最优。目前在以TVS系统为医院内部物流配套建设和科室布局规划领域，相关研究仍存在较大的空白。本文参考某医院建设TVS系统后得到的统计数据进行分析评价，提出改进意见，调整原有布局，使TVS系统运行效率尽可能最大化，并且为以后的TVS系统规划建设提供理论依据。

1 研究对象与模型构建

在医院中，每天都需要完成各种类型的物品运输：血液中心向手术室、住院部输送血液，药房向门诊室提供药品，以及其他如小型医疗包、处方、化验标本、X光片、针剂等的输送。整个过程概念图如图1所示。

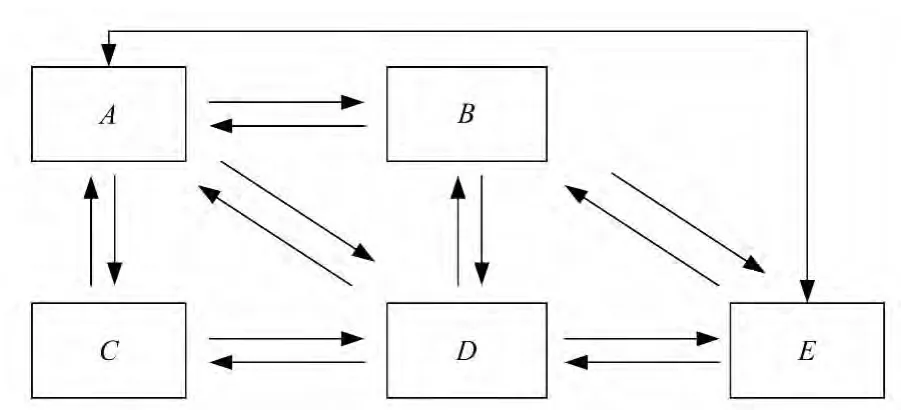
图1 TVS系统传输物品概念图

图1 表示共有ABCDE 5个工作地，它们是确定的并且相互间的距离是已知的，另外有5个科室与之相对应(图中未标出)，且两两科室之间存在着一定的物流量。为研究方便，以Mi(i=1，2，…，n)表示科室，序列M1M2M3M4M5表示科室M1在工作地A，科室M2在工作地B，科室M3在工作地C，科室M4在工作地 D，科室 M5在工作地 E;而M5M1M4M3M2表示M5在工作地A，M1在工作地B，M4在工作地C，M3在工作地D，M2在工作地E。其余以此类推。

借助图1，还可以抽象出两个变量：物流传输系统中科室两两之间的物流量和距离，见表1和表2直观的表示。

表1中的数据是经过统计平均得到的，而表2中的数据则是确定的，因为工作地的位置是固定的。接下来要做的就是对目前的科室布局进行优化。在必要的情况下，重新布局科室所在位置，使得TVS物流传输系统的工作效率尽可能达到最大化。

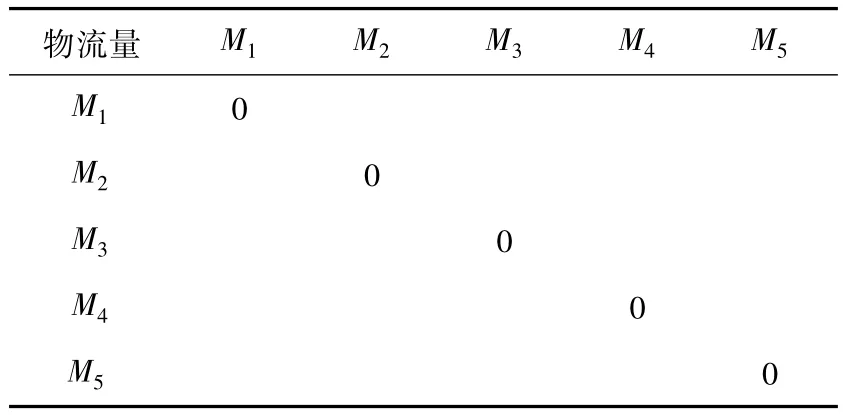
表1 各科室对应的物流量

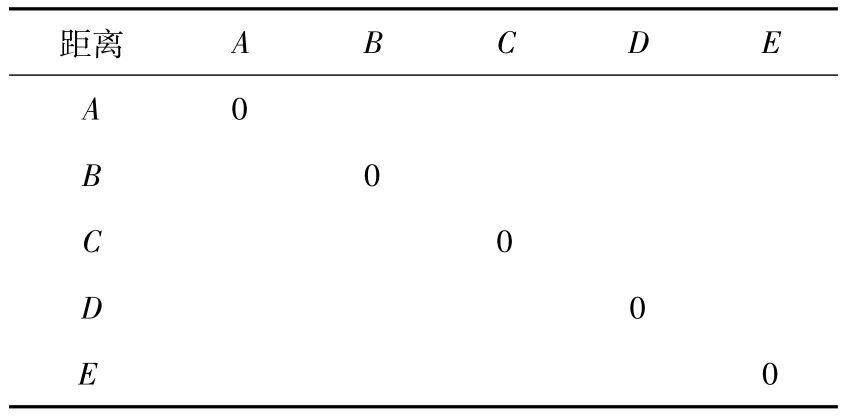
表2 各科室对应的距离

2 二次分配问题的引入

通过前面的分析，可以得出所要研究的内容，简化描述即为：若干个科室需要布置在若干个地方，知道两两科室之间的物流量和距离，如何布置科室使得物流传输系统运行的效率最高，即如何分配才能实现系统总物流量尽可能的小。

这是一个设备布局问题，也是一个典型的二次分配问题(Quadratic Assignment Problem，QAP)。该问题最早源于Koopmans和Beckmann于1957年提出的一类数学模型［2］，纯数学描述为：已知n个作业单位两两之间的物料搬运量大小Wij(i，j=1，2，…，n)，以及n个工作地彼此之间的距离Dij，如何将n个作业单位分配到n个工作地，使得总物流量最小［3-4］，即

最早成功解决二次分配问题的是模拟退火法，之后出现的如禁忌搜索算法、蚁群算法、遗传算法［5］、集群智能算法、神经网络方法都能较好地解决二次分配问题。本文在求解QAP的过程中选择使用遗传算法，并通过eM-Plant自带的遗传算法工具来实现求解过程。

3 基于eM-Plant的仿真与优化

3.1 eM-Plant应用原理概述

eM-Plant软件采用基于面向对象的建模原理，通过建立和运行系统的计算机仿真模型来模仿实际系统的运行状况及其随时间变化的规律。在这个过程中，通过对仿真运行过程的观察和统计，得到仿真输出参数和基本特性，以此估计和推断系统的真实参数和真实性能。eM-Plant使用自定义的目标库来创建具有良好结构的层次化仿真模型，这种模型包括物流和供应链、资源利用率、生产过程、控制策略、分析和优化生产布局等。用户通过扩展的分析工具、统计数据和图表来评估不同的解决方案，并在建设规划的初期阶段作出迅速而又可靠的决策。

3.2 医用轨道物流传输系统仿真与优化

图2为某医院科室平面布局，科室两两之间的传输距离和物流量见表3和表4。下面通过仿真来计算该医院物流系统的初始总物流量，并作出优化。

图2 某医院科室平面布局

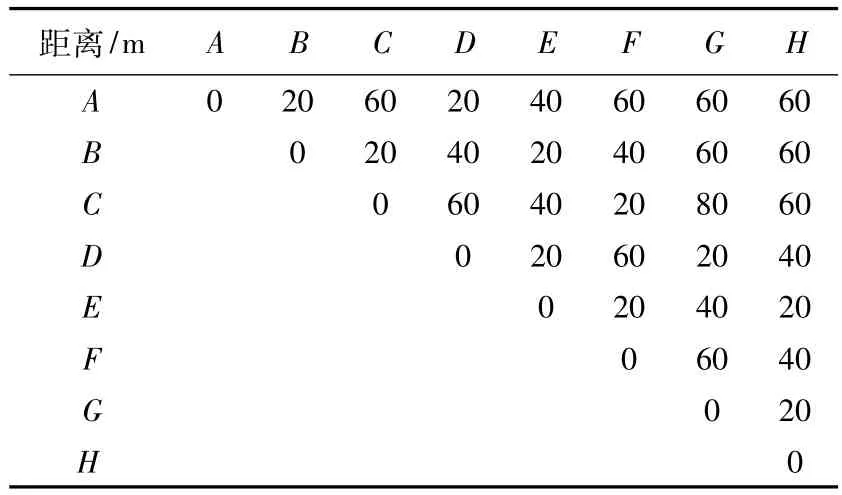
表3 8个工作地对应的距离

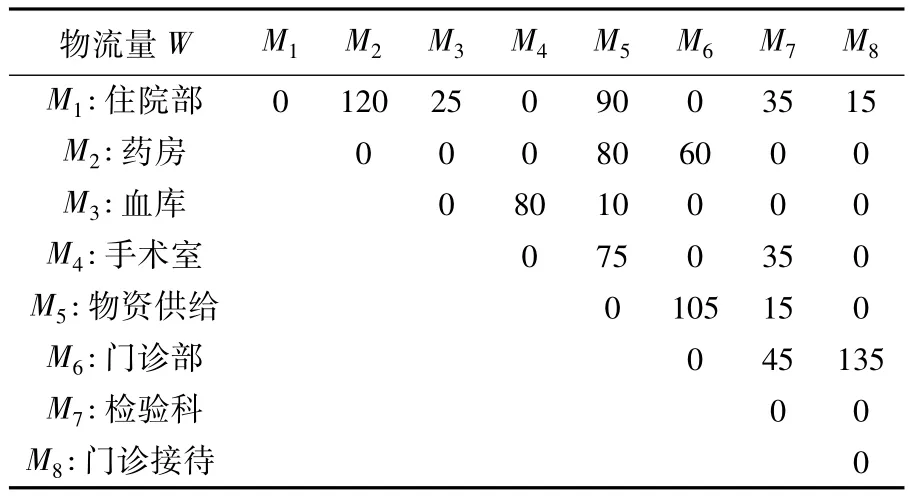
表4 8个科室之间的物流量

按照初始布局，即M1布置在A，M2布置在B，…，M8布置在 H，此时传输系统总物流量 V=∑Wij× Dij=32 700。

根据上文分析，用 eM-Plant建立仿真模型［6］，如图3所示。对初始布局进行仿真，得到初始物流量V0=32 700，与上面计算一致。这说明了仿真模型的正确性和可靠性。再次运行仿真，此次求系统最小物流量。仿真结束后，系统自动生成一份报告，查看报告中的 Optimization problem：Minimum，可以看到系统最小总物流量Best Fitness：26 300，比初始布置时的总物流量32 700小得多，此时对应的序列 Bestsolution：M2M1M7M6M5M3M8M4，即表示将M2分配在A，M1分配在B，…，M4分配在H时，系统总物流量最小，此时物流传输系统的运行效率最佳。