弱刚性钣金件受力下的贴模度仿真分析

2014-09-06石庆兰刘胜兰谭高山

机械设计与制造工程 2014年4期

石庆兰，刘胜兰，谭高山，2

(1．南京航空航天大学机电学院，江苏南京 210016)

(2．安徽工业大学数理学院，安徽马鞍山 243002)

目前，飞机钣金件的外形准确度常用零件内表面与模具贴合间隙的大小即贴模度［1］表示。对这一指标的检测，传统的模拟量传递检测方法为：将被测钣金件与检验样件或检验模等实物进行比对，操作人员通过视觉观察零件外形是否与样件或模胎上刻线相吻合，通过触觉来感知是否与模胎相贴合［2］。随着三维数字化技术的发展，对这一检测过程已逐渐实现了数字化快速检测。

弱刚性钣金件在飞机中得到大量应用，例如蒙皮钣金件是组成飞机外形的主要零件，其刚性弱、外形复杂、不规则、易变形，为了提高对飞机钣金件测量的准确度和了解使用过程中的应力分布，需要对其进行受力下的分析。对成形后的钣金件进行受力变形分析，一定载荷下的贴模度检测为其中的一项重要内容。

随着CAE技术的发展，有限元分析软件的使用不仅可避免反复试验，减少对工艺人员生产经验的依赖，而且能够预测成形过程中可能出现的一些缺陷，对工艺方案进行优化，使得钣金成形技术水平有一个质的飞跃［3］。目前的有限元分析技术还停留在对零件设计模型的分析计算上，针对已有成品件进行有限元仿真的研究目前并不多见。本文在数字化测量与检测的基础上，结合有限元仿真软件，计算弱刚性钣金件受力下的贴模度，同时分析各节点的等效应力。

1 检验方法

蒙皮钣金件在检测过程中允许一定范围内的弹性变形。原航空工业标准文件“飞机钣金件尺寸公差及技术条件”(HB 6470-90)［4］对该类零件的检测给出了加压检测标准。飞机蒙皮钣金件外形准确度检测中，加压条件下钣金件贴模度测量方法如图1所示［4］。将被测钣金件与检验模具位置对齐以后，在某一个合适的位置加载一定的力，然后测量贴模度。

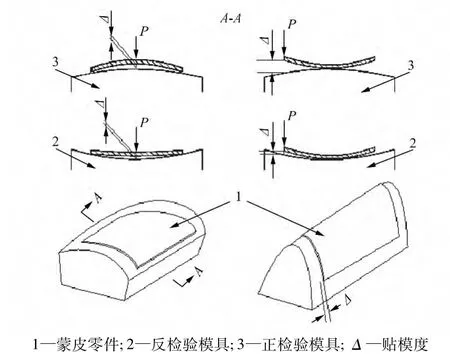
图1 加压检验下的零件贴模度测量

目前该标准仍然是航空企业检测弱刚性钣金件的重要依据，但通常的数字化测量与分析方法只能得到自然状态下的贴模度误差检测数值，无法满足载荷下的贴模度计算要求。本文将对这一加压下的检测过程进行有限元仿真模拟。蒙皮零件模型用其下表面测量数据描述，其格式为三角网格结构，三角网格结构是有限元分析中常见的一种网格划分形式，符合有限元分析的要求。使用光学扫描仪获得的数据网格非常密集、不均匀，需要经过一定的处理才可进行分析。检验模具模型采用理论设计检验模型表示，为自由曲面。

2 贴模度受力仿真过程

图2(a)为某一钣金件检验模胎的设计模型，图2(b)为光学扫描获得的三角网格形式的测量数据模型。根据飞机蒙皮钣金件相对检验模具的贴模度测量方法，该零件(外形尺寸参数为700mm×200mm×1．6mm)可在某一个合适的位置加载一个50N的力。在实际检测过程中，主要是工人师傅凭经验在某个位置放一个重50N的沙包，然后再进行检测。对这一过程进行仿真，首先要对测量数据进行处理。

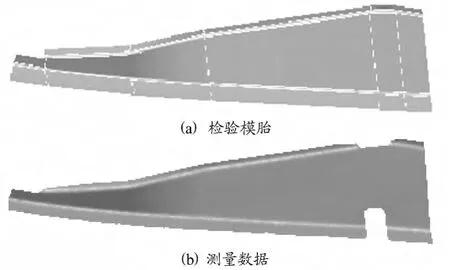
图2 钣金件模型

2.1 测量数据处理

通常情况下，采用光学扫描仪获得的钣金件内表面三角网格数据不均匀，存在大量的冗余数据，甚至有不少狭长三角片的存在，并不满足有限元分析软件对网格质量的要求。需要对其进行均匀化处理。对测量数据进行均匀化处理的方法很多，要获得均匀程度比较高的结果数据最简单的方法是对其均匀采样，给定某个采样距离，即可获得采样后的数据点，然后对采样数据点进行网格化便可得到均匀的三角网格，结果如图3所示。

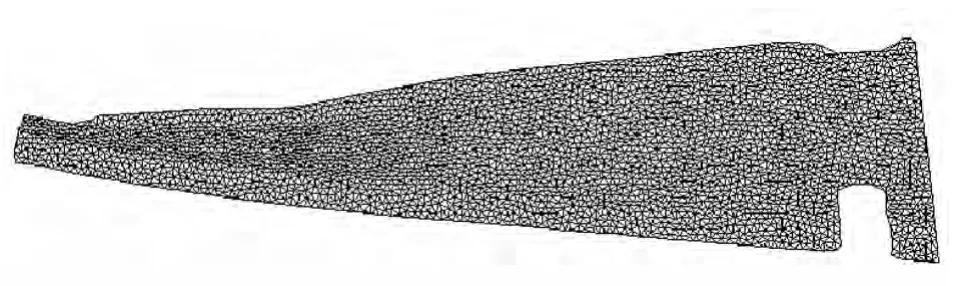
图3 钣金件表面数据均匀化处理结果

测量数据位于测量坐标系中，而检验模胎位于设计坐标系中，在进行有限元仿真之前必须将两个模型对齐，以统一坐标系。对模型对齐的研究最早由ChenY［5］、BeslP［6］等人提出，随着研究的不断深入，目前常用的逆向软件，如Imageware、Geomagic已实现模型对齐功能。使用逆向软件将模型对齐后，沿外法矢方向移动测量数据至数据点全部位于检验模胎上侧，使之符合零件对模胎的贴合要求。对齐后进行贴模度误差分析，即计算每个测量数据点到理论模型的最近距离，如图4所示。

图4 自然状态下的贴模度误差图

2.2 参数设定

按照有限元分析的一般步骤。首先导入零件测量数据模型和检验模胎模型。测量数据模型为三角网格格式，导入后不需要进行网格化。检验模胎模型为自由曲面格式，需要进行网格划分。两者均为壳单元，测量数据模型单元类型为线性三角形单元，模胎模型单元类型为二次四边形缩减积分单元。

参数设定中的材料属性：钣金件的材料为LY12，其杨氏模量为70GPa，泊松比为0．3。截面属性：均质壳单元，模型厚度为1．6mm，测量数据模型壳偏移为底部表面，模胎模型壳偏移为顶部表面。完成材料属性的设置后，对测量数据和模胎进行装配，由于之前二者坐标系已经统一，因此无需平移旋转等操作，只需要将两个部件进行实例化操作即可。采用静力通用分析步，求解方法为默认。相互作用属性中定义类型为接触，属性为力学切向行为，摩擦系数为0．3。相互作用类型为表面与表面接触，主表面选择模胎表面，从表面为测量数据表面，滑移公式为小滑移。边界条件设置中模胎为刚体，固定住6个自由度。

从图4中可以看出，零件两端部分比较贴模，而中间有一个区域鼓起比较厉害，最大误差值为4．25mm。因此加载力的位置应为贴模度误差数值比较大的区域(如图5所示)，施加一个合力为50N的均布载荷，方向垂直于零件表面向下，进行仿真计算。

图5 加压位置

2.3 仿真结果分析

加压前后贴模度误差值如图6和图7所示。由图可见，在50N合力的作用下，该零件贴模度最大值由4．245mm减小到了3．499mm。

图6 加压前贴模度误差(单位mm)

图7 加压后的贴模度误差(单位mm)

施加载荷的具体位置在检测标准中并未给出，实际检测时更是没有准确的方法，有些时候零件某个地方隆起，加压位置却是在旁边的位置。数值模拟正是一种可以通过对不同位置施加载荷来确定位置的方法。因此可在其他位置进行同样的分析，对多次结果进行比较，确定出最合适的加载位置。对批量生产的零件而言，由于其成形工艺参数相同，通过对几个零件的加载结果分析可以很容易确定其余零件的最佳受载位置。

最后可进一步了解各节点的等效应力分布，如图8所示。最大应力为43．74MPa，远小于该零件材料的弹性极限 σe=325MPa。进一步说明在50N力作用下的变形属于弹性变形。