基于高斯逼近的广义B样条平滑滤波快速算法

申 丁，高诚辉，2，任志英，2

(1．福州大学机械工程及自动化学院，福建福州 350108)

(2．福州大学摩擦学研究所，福建福州 350002)

在描述和评价三维表面特征中，基准信息的提取一直是重中之重，它直接影响最后粗糙度评定的精确程度。目前使用的方法主要有中线法、相移滤波法(RC法)、高斯滤波、样条滤波等。ISO11562与ISO16610都提出以高斯滤波器作为标准滤波器［1-2］，其优势在于它的零相位和无相位畸变等优点，但它也存在边界畸变、计算速度相对较低等不足之处。为了解决边界畸变问题，ISO16610-22提出用标准样条滤波器替代高斯滤波器［3］，但其计算效率不高，因此在工业中的应用十分有限。由于B样条滤波器在截止波长λc处有超过99．99%的截止率，2006 年 Munetoshi Numada［4］基于 B 样条滤波提出了相应的频域滤波法，不仅提高了计算速度，而且较好地抑制了边界畸变。但B样条滤波器和高斯滤波器的传输特性不同，若给同一表面进行滤波会得到不同的粗糙度参数值。为此，文献［5］提出了相应的光滑滤波算法，通过B样条滤波器逼近来实现高斯滤波，不仅大大减少了计算量，而且对标准高斯滤波有较高的逼近度。但此方法需要通过多个滤波器联级实现逼近，这就意味着要经过多次循环计算才能得到高度逼近的基准面。本文将广义B样条滤波器和平滑滤波算法相结合，在保证逼近精度要求的同时，通过优化传递函数中的参数t1，t2，不借助级联实现其对标准高斯滤波器的逼近，减少了计算量，为今后三维表面粗糙度评定打下了良好的基础。

1 算法的理论基础

1.1 广义B样条滤波器

由线性微分方程推导出的广义B样条函数，其定义如下［6］：

广义B样条函数滤波过程同B样条滤波一样，实际上也可以看成一种插值逼近过程，在给定范围［x0，xn］内，广义B样条函数可以构造一系列函数来逼近目标函数。其公式如下：

式中：sn(x)是插值函数;c(x)是插值系数。

根据式(3)，实测信号f(i)可由一系列的广义B样条基函数β3r

1(i-k)(k∈Z)线性表示。确定实际分解系数C(i)的过程就相当于分解过程，称为直接B样条变换;而利用广义B样条基函数来表示实测信号的过程称为间接B样条变换。

1.2 高斯滤波器

根据ISO11562规定，高斯滤波权函数表示为［1］：

式中：wc=2πΔx/λc;e为自然对数的底。

1.3 逼近高斯的广义B样条平滑滤波器

表面轮廓基准的确定作为粗糙度评定的首要任务，其过程可看作是对实测数据的平滑处理。因此学者们在变分原则基础上，提出了平滑变分公式［7］：

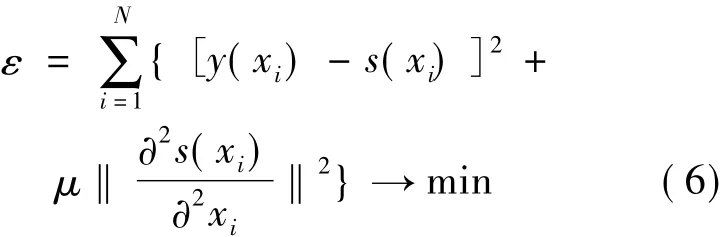
式中：y(xi)为实测数据;s(xi)为滤波后基准数据;为曲线弯曲能量的范数，代表基准的平滑性，而［y(xi)-s(xi)］2侧重于滤波后的基准与原始轮廓的逼近程度;μ为拉格朗日常数，用来平衡逼近程度和基准的平滑性。

1989 年，Johannes［8］向式(6)中添加速度项以提高逼近速度，其等式如下：

式中：τ为调节参数。

将式(8)关于C(xi)偏微分求导，同时代入差分算子(其中，二阶差分算子d(2)(xi)=δo(xi+1)-2δo(xi) + δo(xi-1)，一阶差分算子 d(1)(xi) =δo(xi)-δo(xi-1))，即可求出平滑样条系数C(xi)，其等式如下：

再根据间接B样条变化，即可求得轮廓的基准信息：

将式(10)转换为Z域表达式：

式中：M为采样点总数。

2 改进的算法——逼近高斯的广义B样条平滑滤波器特性

对式(11)进行傅里叶变换(即将式(11)中的z用e-jwt替代)，可求出平滑广义B样条滤波器的频域响应。其等式如下：

目前提高逼近程度的方法主要是通过滤波器级联实现［5］，但是由于广义B样条函数的传递函数中含有可变参数t1，t2，因此在实际工程应用中通过修正其取值，可以在不级联的情况下，同样提高其逼近程度。这就意味着滤波过程中，在最短的时间内得到满足精度要求的轮廓基准。根据ISO11562规定，滤波器在截止波长 λc(λc=2πΔx/wc)处的传输率为50%，因此式(13)必须满足如下关系：

将式(15)与式(13)联立，即可得到平滑广义B样条函数的频域响应公式。为了得到最佳逼近滤波器，建立以w(i)为自变量的目标函数，其中w(i)∈(0，π)，t1∈ (0，+ ∞)，t2∈ (0，+ ∞)。

从式(13)和公式 wc=2πΔx/λc可以看出，广义B样条平滑滤波器对标准高斯滤波器的逼近不仅与t1，t2有关，而且在不同取样间隔Δx情况下，逼近的程度也不同。为了方便起见，以wc为对象进行讨论。本文在不同的截止角频wc下运用PSO(粒子群算法)求解t1，t2的最优值，使两种滤波器之间幅频偏差达到最小化。本文分别列出wc=0．01，wc=0．10和wc=1．00时，广义B样条滤波器与高斯滤波的传输特性及其之间的偏差，如图1～图6所示。

图1 高斯滤波器与广义B样条平滑滤波器(wc=0．01)

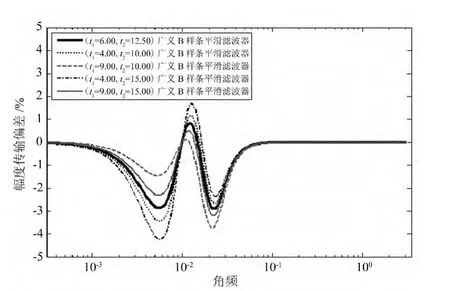
图2 不同参数的滤波器的幅度传输特性偏差(wc=0．01)

图3 高斯滤波器与广义B样条平滑滤波器(wc=0．10)

图4 不同参数的滤波器的幅度传输特性偏差(wc=0．10)

图5 高斯滤波器与广义B样条平滑滤波器(wc=1．00)

图6 不同参数的滤波器的幅度传输特性偏差(wc=1．00)

图1 ～图6分别描述了在不同截止角频wc的情况下，广义B样条滤波器与高斯滤波的幅度偏差比较。图1为当wc=0．01时，标准高斯滤波器和参数t1，t2在不同情况下广义B样条滤波器的传输特性曲线。从图2的传输幅度偏差可以看出，当t1=6．00，t2=12．50时，广义B样条滤波器与标准高斯滤波器的偏差小于3%;从图3和图4可以看出，当 wc=0．10，t1=1．01，t2=0．36 时，广义 B 样条滤波器与标准高斯滤波器的偏差小于2．8%;从图5 和图 6 可以看出，当 wc=1．00，t1=6．87，t2=1．90时，广义B样条滤波器与高斯滤波器的偏差小于1%(明显小于ISO11562规定的5%)。这表明随着wc的提高，参数优化的广义B样条滤波器逼近标准高斯滤波器的程度越来越高，即在满足奈奎斯特定理的条件下(采样频率必须大于或等于2倍信号谱的频率，即1/λ ＜ 1/(2Δx)，wc≤ π)，适当保持wc在较高的水平，广义B样条滤波器的逼近效果就越明显。本文发现wc=1．00左右最为合适，因为在表面评定中的标准高斯滤波器存在滤波过渡区。当wc趋于π时，位于截止角频右边的过渡区超出π以外，起不到滤波的作用。

3 实验分析

为了验证算法的可行性，对一实际零件表面进行了测量，其中截止波长λc=80μm，采样间距为0．5μm，共测量19 000个数据点。其原始轮廓如图7所示。

图7 原始表面轮廓与两种滤波基准线比较图

根据上述广义B样条平滑滤波算法，其中共轭滤波器的参数分别为 b1=0．476 8，b2=-0．096 5，A=1-b1-b2。图7 中灰色实线与白色方形实点分别为实测轮廓和高斯滤波基准，黑色细线为本文算法滤波基准。为了抑制边界处的畸变，高斯滤波分别对边界处滤波窗内的权值重新归一化［9］。从图7可以看出，本文方法与高斯滤波的结果十分接近，所述方法同样具有抑制边界畸变的能力，且整个滤波过程耗时只有1．6ms左右，仅为高斯滤波(整个过程耗时70ms左右)的1/40。

4 结束语

本文借助平滑变分公式和广义B样条函数，实现B样条滤波对标准高斯滤波器的逼近，整个运算过程不存在任何级联运算，很大程度上提高了运算效率。同时，由于滤波窗尺寸较小，对边界畸变存在一定的抑制作用。

［1］ ISO11562-1996 Geometrical Product Specification(GPS)-Surface Texture：Profile Method-Metrological Characteristics of Phase Correct Filters［S］．

［2］ ISO16610-21，2011 Geometrical Product Specifications(GPS)-Filtration：Linear Profile Filters：Gaussian Filters［S］．

［3］ ISO16610-22，2006 Geometrical Product Specifications(GPS)-Filtration：Liner Profile Filters：spline Filters［S］．

［4］ Munetoshi Numda，Takashi Nomura，Kazuhide Kamiya，et al．Filter with variable transmission characteristic for determination of three-dimensional roughness［J］．Precision Engineering，2006，30(4)：431-442．

［5］ 张浩，袁怡宝，张峰．基于B样条滤波器的表面粗糙度提取方法［J］．纳米技术与精密工程，2009(11)：490-495．

［6］ Unser M，Aldroubi A，Edem M．B-spline signal process：Part ITheory［J］．IEEE Transaction on Signal Processing，1993，41(2)：821-832．

［7］ Schoenberg I J．Spline functions and problem of graduation ［J］．Proc．Nat．Acad．Sci．1964，52(4)：947-950．

［8］ Johannes P F，D＇HAEYER．Gaussian filtering of images：a regularization approach［J］．Signal Processing，1989，18(2)：169-181．

［9］ Brinkmann S，bodschwinna H，Lemke H-W．Accessing roughness in three-dimensions using gaussian regression filtering［J］．Machine Tools and Manufacture，2001，41(13)：2153-2161．

［10］胡广书．数字信号处理［M］．1版．北京：清华大学出版社，1997．

［11］张浩，袁怡宝，张峰，等．广义B样条滤波器在表面形貌测量中的应用［J］．光学精密工程，2008(9)：1722-1726．