Sensitivity analysis for stochastic user equilibriumwith elastic demand assignment model

Wang Jian Wu Dingxin Deng Wei

(1School of Transportation, Southeast University, Nanjing 210096, China)(2Lyles School of Civil Engineering, Purdue University, West Lafayette 47906, USA)(3Faculty of Transportation Engineering, Huaiyin Institute of Technology, Huai’an 223001, China)



Sensitivity analysis for stochastic user equilibriumwith elastic demand assignment model

Wang Jian1,2Wu Dingxin1,3Deng Wei1

(1School of Transportation, Southeast University, Nanjing 210096, China)(2Lyles School of Civil Engineering, Purdue University, West Lafayette 47906, USA)(3Faculty of Transportation Engineering, Huaiyin Institute of Technology, Huai’an 223001, China)

This paper puts forward a rigorous approach for a sensitivity analysis of stochastic user equilibrium with the elastic demand (SUEED) model. First, proof is given for the existence of derivatives of output variables with respect to the perturbation parameters for the SUEED model. Then by taking advantage of the gradient-based method for sensitivity analysis of a general nonlinear program, detailed formulae are developed for calculating the derivatives of designed variables with respect to perturbation parameters at the equilibrium state of the SUEED model. This method is not only applicable for a sensitivity analysis of the logit-type SUEED problem, but also for the probit-type SUEED problem. The application of the proposed method in a numerical example shows that the proposed method can be used to approximate the equilibrium link flow solutions for both logit-type SUEED and probit-type SUEED problems when small perturbations are introduced in the input parameters.

network modeling; stochastic user equilibrium; elastic demand; sensitivity analysis; first-order approximation

Sensitivity analysis is defined as a technique used to determine how the different values of independent variables impact a particular dependent variable under a given set of assumptions. In network modeling, it is constantly used for estimating the changes of objectives at macroscopic levels (i.e., network performance) caused by the variations in the objectives in macrocosmic levels (i.e., signal splits). The possible application of this method includes, but is not just restricted to, the first-order equilibrium solution approximation, critical parameter identification, parameter uncertainty analysis and effectiveness diagnosis.

The research on sensitivity analysis for traffic assignment models can be traced back to the work done by Hall[1]. He investigated the direction of change when perturbations are added to the inputs of a user equilibrium traffic assignment model. Tobin and Friesz[2]overcame the problem of the non-uniqueness of the user equilibrium path flows by introducing an equivalent restricted program that has the desired uniqueness properties. Following their work, Yang[3]derived a gradient-based sensitivity analysis formula for network equilibrium problems with elastic demand. However, this method has several significant deficiencies that it is only applicable to non-degenerated point (equilibrium flows should be strictly positive), and the assumption that the link travel cost increases monotonously with respect to the link flow is also stronger than necessary. A detailed description of those deficiencies and the corresponding technique for improvement can be found in Ref.[4]. For the sensitivity analysis of logit-based stochastic user equilibrium (SUE) problem, Ying and Miyagi[5]formulated a computationally efficient link-based algorithm by adopting Dial’s algorithm[6]. Clark and Watling[7]proposed a more generous method for sensitivity analysis of the SUE assignment model, which is actually a direct application of the first-order sensitivity approximation method for a general nonlinear program proposed by Fiacco[8]. The method can not only observe the changes of the equilibrium link flows with respect to uncertainty parameters at logit-based SUE but also can be equally applied for probit-based SUE.

The aforementioned literature mainly focused on addressing the sensitivity analysis problem for UE and SUE assignment models as well as some combination models. Based on our knowledge, no research has been conducted on implementing the sensitivity analysis of SUE with the elastic demand (SUEED) traffic assignment model. This paper aims to formulate a method for a sensitivity analysis of SUEED models with the gradient-based method.

1 SUEED Problem

The SUEED model assumes that, in the equilibrium state, route or link choices should be such that an SUE is formed, and, meanwhile, the demand between each O-D pair (used in the SUE assignment) must be consistent with travel costs between each O-D pair[9]. Maher et al.[9]proposed an equivalent unconstrained mathematical program for the SUEED problem, which is formulated as

(1)

2 Sensitivity Analysis for SUEED Assignment Problem

2.1 Sensitivity analysis for general nonlinear programming

Fiacco[8]made a significant contribution to the sensitivity analysis of nonlinear programming.

s.t.p(ε)gi(x,ε)≥0i=1,2,…,mhj(x,ε)=0j=1,2,…,n

(2)

2.2 Sensitivity analysis method for SUEED problem

(3)

where

(4)

(5)

(6)

whereSis the vector of all expected perceived O-D travel times;tis the vector of all link travel times. Assume thatεis a perturbed parameter in the SUEED problem. MatrixN(ε) in Eq.(2) is then extended as

Note that

(8)

(9)

wherePrsis the vector of all the route choice probabilities between the O-D pairr-s;D-1(q) denotes the vector of all inverse functions of the O-D demand function. The mixed derivatives ofZ(q,ε) with respect to link flowvband perturbed parameterεis

(10)

Simplifying Eq.(10) yields

(11)

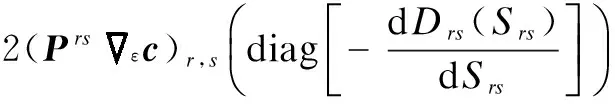
(12)

3 Numerical Application

The example network shown in Fig.1 is used to demonstrate how to apply the sensitivity analysis method. This network has two O-D pairs, seven links and six nodes, of which nodesEandFare signal-controlled intersections. There are three paths for O-D pairAB, that is, route 1:AEB; route 2:AFBand route 3:AEFB, and only one path,CEFDfor O-D pairCD.

The current O-D demands are assumed to be 18 veh/min and 6 veh/min for O-D pairsABandCD, respectively. The link travel cost and its corresponding input data are

Fig.1 The example road network

summarized in Tab.1. IntersectionsEandFare supposed to be controlled by two independent signal splits,λ1andλ2. The elastic demand functions for O-D pairsABandCDin this numerical example are specified as

qAB=DAB(SAB)=50exp(-0.5SAB)

(13)

qCD=DCD(SCD)=30exp(-0.2SCD)

(14)

Tab.1 Input data to the example network

3.1 Sensitivity of logit-type SUEED problem

The signal splits are set asλ1=λ2=λ3=λ4=0.5 to start a test. Letθbe the discrete parameter in the logit-type SUEED problem. The numerical results including equilibrium link flows, O-D demands and the Jacobian matrix of route choice probabilities calculated atθ=1 are presented as

Assume thatλ1is a perturbed parameter in the road network, and then according to Eqs.(3), (4), (5) and (12), matrixMand matrixNcan be calculated correspondingly. Then using Eq.(2), the sensitivity of the equilibrium link flow and O-D demand solutions with respect to signal splitλ1is obtained as

(15)

Eq.(15) has plentiful physical meanings and can be used to develop a first-order approximation of the perturbed solution for small changes in signal splitsλ1, given as

(16)

Fig.2 describes the comparison of estimated link flow calculated by Eq.(16) and the exact link flow. The linear nature of the approximation procedure given here is clearly evident. The further the signal split from the initial solution value, the greater the deviation between the exact and approximate solutions.

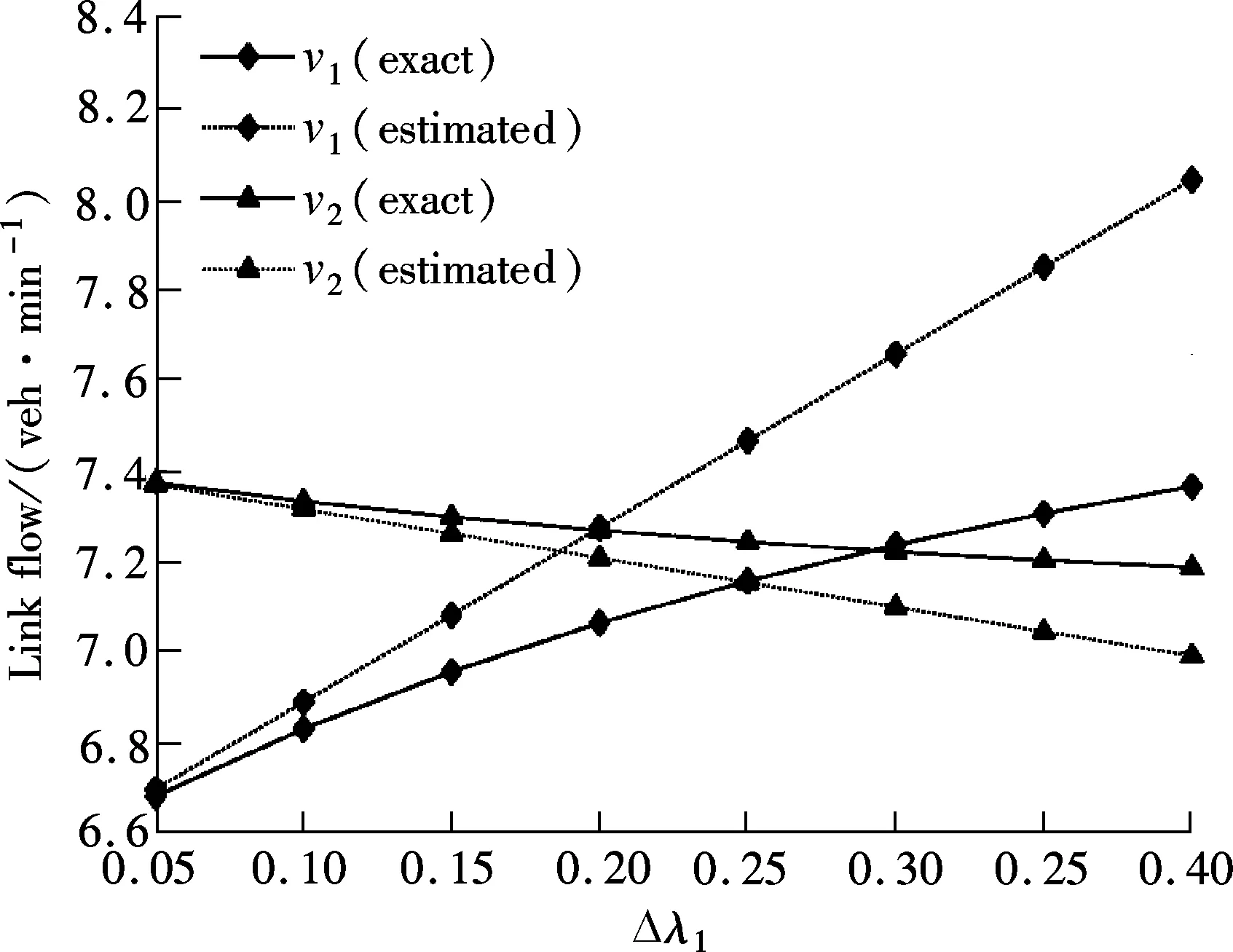
Fig.2 Exact and approximated equilibrium solutions for the logit-type SUEED (signal split change)

3.2 Sensitivity of probit-type SUEED assignment problem

For the probit-type model, the link travel time is assumed to be normally distributed with a mean equal to the measured link travel time and with variance that is proportional to the measured link travel time. In other words,

Ta～N(ta,αta)

whereαis the variance of the perceived travel time over a road segment of unit travel time. The covariance of route travel time then will be subject to a multivariate normal distribution as follows:

Crs～MVN(tΔrs,αΔrstΔrsT)

The equilibrium link flows, O-D demands and the Jacobian of route choice probabilities calculated with the MSA method atα=1,λ1=λ2=λ3=λ4=0.5 are specified as

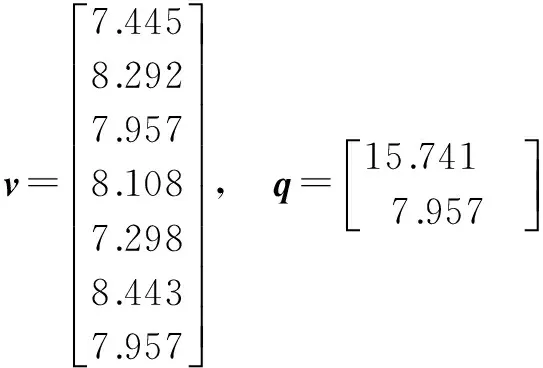
Assume that there is a perturbation in the input parameterλ1. Similarly, by using the derivatives of Eq.(2), the sensitivity of the link equilibrate solutions with respect to input parameterλ1can be calculated. The linear approximation to the solution for a small change in signal splitλ1is thus presented as

(17)

Eq.(17) denotes that an increase in signal splitsλ1will lead to different change patterns in the output parameters. The demand between O-D pairABand the equilibrium flow on link 1 and link 5 will benefit most from the increased signal splitsλ1while the equilibrium flow on link 2 and link 6 are reduced significantly.

According to Eq.(17), the exact and estimated equilibrium route flow solutions are drawn in Fig.3. As can be seen, the estimated route flows are very close to corresponding exact values, which implies significant potential use in practice. If high accuracy is not requested, the sensitivity analysis method will be a good alternative to approximate the equilibrium solutions when changes are introduced to the network input parameters, which also saves much effort being required to re-solve the assignment. But it should be noted that the accuracy of the estimated equilibrium patterns is significantly dependent on the perturbations itself. The larger the perturbation introduced, the greater the divergence between the exact and approximate solutions will be.

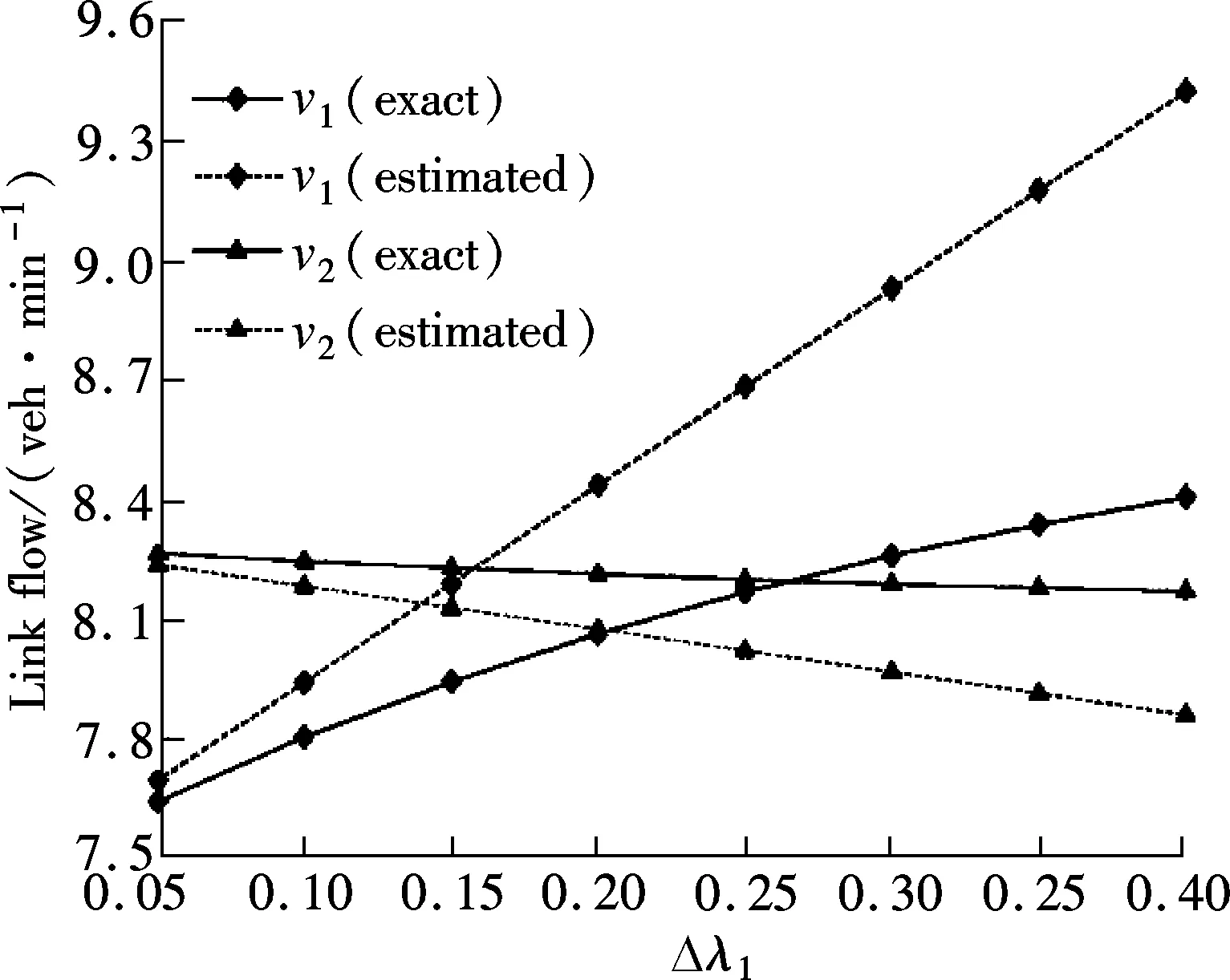
Fig.3 Exact and approximated equilibrium solutions for probit-type SUEED (signal split change)

4 Conclusion

This paper develops a computationally efficient method for the sensitivity analysis of the SUEED assignment problem put forward by Maher et al[9]. Proof is given that the SUEED assignment problem satisfies all the conditions required for the sensitivity analysis of a general nonlinear problem. Explicit expressions are then given for obtaining the derivatives of equilibrium solutions with respect to input parameters by taking advantage of the gradient-based method. Those expressions are not only applicable for the sensitivity analysis of the logit-type SUEED problem but also can be equally applied to the probit-type SUEED problem. Numerical examples are presented to demonstrate how to obtain the derivatives of equilibrium solutions with respect to perturbed parameters with both logit and probit assumptions. These derivatives can be used to approximate the changes in solution variables when the network characteristics are changed slightly. Further research is to explore the applicability and efficiency of the propose method in various applications such as critical parameters identification, paradox and network uncertainty analysis.

[1]Hall M A. Properties of the equilibrium state in transportation networks[J].TransportationScience, 1988, 12(3): 208-216.

[2]Tobin R L, Friesz T L. Sensitivity analysis for equilibrium network flows[J].TransportationScience, 1988, 12(4): 242-250.

[3]Yang H. Sensitivity analysis for the elastic-demand network equilibrium problem with applications[J].TransportationResearchPartB:Methodological, 1997, 31(1): 55-70.

[4]Josefsson M, Patriksson M. Sensitivity analysis of separable traffic equilibrium equilibria with application to bi-level optimization in network design[J].TransportationResearchPartB:Methodological, 2007, 41(1): 4-31.

[5]Ying J Q, Miyagi T. Sensitivity analysis for stochastic user equilibrium network flows—a dual approach[J].TransportationScience, 2001, 35(2): 124-133.

[6]Dial R B. A probabilistic multipath traffic assignment model which obviates path enumeration[J].TransportationResearchPartB:Methodological, 1971, 5(2): 88-111.

[7]Clark S D, Watling D P. Probit-based sensitivity analysis for general traffic networks[J].TransportationResearchRecord, 2001, 1733: 88-95.

[8]Fiacco A V.Introductiontosensitivityandstabilityanalysisinnonlinearprogramming[M]. New York: Academic Press, 1983.

[9]Maher M J, Hughes P C, Kim K S. New algorithms for the solution of the stochastic user equilibrium assignment problem with elastic demand[C]//Proceedingsofthe14thInternationalSymposiumonTransportationandTrafficTheory. Jerusalem, Israel, 1999: 265-286.

弹性需求下随机用户均衡分配问题敏感性分析

王 建1,2吴鼎新1,3邓 卫1

(1东南大学交通学院, 南京 210096)(2Lyles School of Civil Engineering, Purdue University, West Lafayette 47906, USA)(3淮阴工学院交通运输学院, 淮安 223001)

提出了一种对弹性需求下随机用户均衡(SUEED)分配问题进行敏感性分析的方法.首先,证明了SUEED模型在均衡解处输出变量对扰动参数的可导性.其次,通过采用对一般非线性规划问题进行敏感性分析的梯度下降法,建立了SUEED模型中设计变量在均衡流量解处对扰动参数的计算公式.这些公式不仅可以对logit型SUEED问题进行敏感性分析,而且同样适用于probit型SUEED问题.算例路网的应用研究发现，所提出的方法可有效估计logit型SUEED问题和probit型SUEED问题中输入变量扰动后的均衡流量解.

网络建模;随机用户均衡;弹性需求;敏感性分析;一阶估计

U491.1

s：The Scientific Innovation Research of College Graduates in Jiangsu Province (No.CXLX13_110), the Young Scientists Fund of National Natural Science Foundation of China (No.51408253), the Young Scientists Fund of Huaiyin Institute of Technology (No. 491713328).

：Wang Jian, Wu Dingxin, Deng Wei. Sensitivity analysis for stochastic user equilibrium with elastic demand assignment model[J].Journal of Southeast University (English Edition),2014,30(3):363-367.

10.3969/j.issn.1003-7985.2014.03.020

10.3969/j.issn.1003-7985.2014.03.020

Received 2013-12-05.

Biographies：Wang Jian (1988—), male, graduate; Deng Wei (corresponding author), male, doctor, professor, dengwei@seu.edu.cn.