用变分迭代法解分数阶微分方程组
2014-09-06王长佳李辉来
代 群,王长佳,李辉来
(1.长春理工大学 理学院,长春130022; 2.吉林大学 数学学院,长春 130012)
用变分迭代法解分数阶微分方程组
代 群1,王长佳1,李辉来2
(1.长春理工大学 理学院,长春130022; 2.吉林大学 数学学院,长春 130012)
用变分迭代法求解一类分数阶微分方程组,并改进了校正函数.数值结果表明,运用变分迭代法求解分数阶微分方程组的近似解有效且准确.
分数阶导数; 方程组; 变分迭代法; 校正函数
0 引 言
分数阶微积分广泛应用于自然科学和工程技术等领域,但绝大多数分数阶微分方程的准确解很难找到,因此研究分数阶微积分的数值和解析算法十分必要.目前,同伦分析法已成功应用于许多非线性问题中,如非线性Vakhnenko方程[1]和分数阶KdV-Burger-Kuramoto方程[2]等.文献[3-4]将Adomian分解法应用于求解线性和非线性分数阶微分方程中; Odibat等[5]提出了修正的同伦摄动法,并将其应用于求解分数阶Riccati微分方程中.Momani等[6]将变分迭代法应用于求解一类分数阶微分方程中.
本文对变分迭代法进行推广,采用新的校正函数形式,将其应用到下列分数阶微分方程组中:
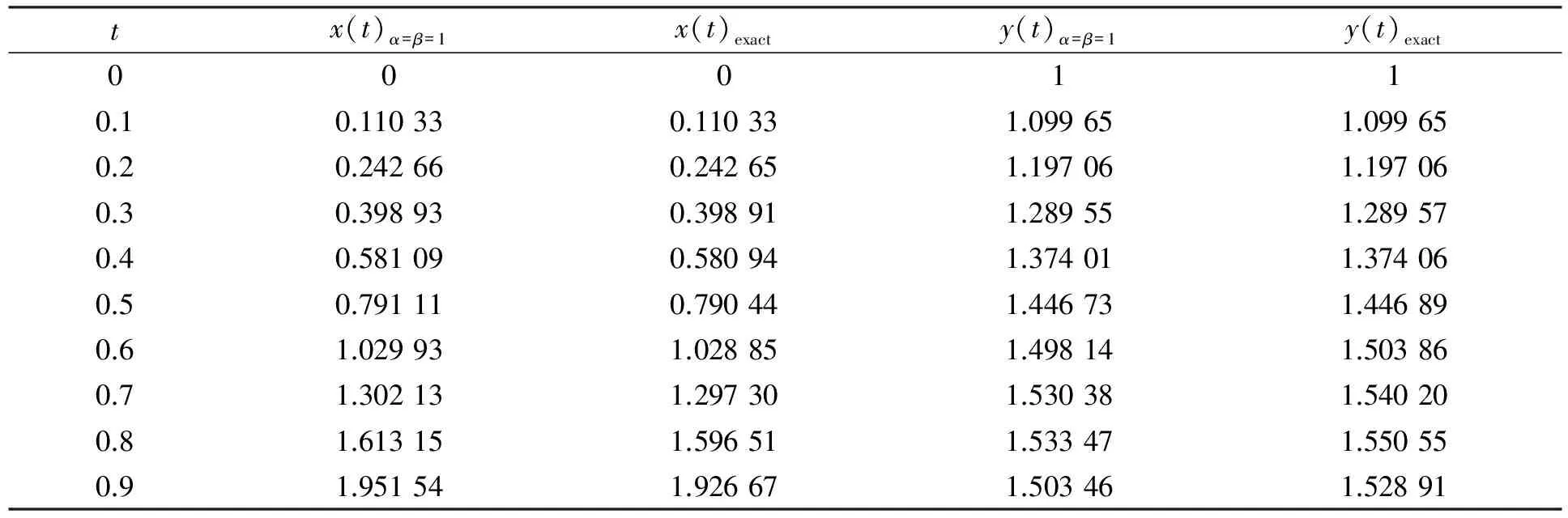
其中Dai是Caputo分数阶导算子,0 设Cμ={f(x)|f(x)|=xpg(x),g∈C[0,+∞),p>μ},对于f∈Cμ,定义α阶的Riemann-Liouville分数阶积分算子[7]Jα如下: 其中J0f(x)=f(x). Caputo分数阶导算子Dα定义[7]如下: 其中:m-1<α≤m,m∈;x> 变分迭代法不需要线性化和离散化,它能提供分析解显而易见的符号项和数值近似解,可以应用到线性和非线性问题中. 非线性分数阶微分方程可写成下列形式: Nu+Lu=g(t), 其中:L为线性算子;N为非线性算子. 根据变分迭代法[6],可建立n+1阶校正函数: 不妨设方程组(1)的第i个分数阶微分方程可写成下列形式: Dαixi=Nxi+Lxi+g(t). (3) 建立方程(3)的n+1阶校正函数: (4) 例1考虑如下线性分数阶微分方程组: 初始条件: 当α=β=1时,方程组的准确解为 由变分迭代法(4),建立方程组(5)-(6)的n+1阶校正函数为: 由变分理论和式(7),有 从而 解得λ1(τ)=-et-τ.同理由式(8)可得λ2(τ)=-et-τ.结合广义Taylor展式[8]可分别得方程组解的迭代公式: 从而可得近似解: 表1列出了用变分迭代法求解方程组(5)(取α=β=1)的第3阶近似解和精确解的值.由表1可见,当α=β=1时,方程组(5)的近似解与准确解高度一致.本文仅计算了第3阶的近似解,如果想提高近似度,可以利用变分迭代法计算更高阶的近似解. 表1 方程组(5)中当α=β=1时第3阶近似解和精确解的值Table 1 Third-order approximate and exact solutions for system (5) obtained at the values of α=β=1 例2考虑如下线性分数阶微分方程组: 初始条件: 当α=β=1时,方程组的准确解为 由变分迭代法(4),建立方程组(9)-(10)的n+1阶校正函数为: 由变分理论和式(11),有 解得λ1(τ)=-e(t-τ)/2.同理由式(12)可得λ2(τ)=-et-τ.结合广义Taylor展式分别可得方程组解的迭代公式: 从而可得近似解: 表2列出了用变分迭代法求解方程组(9)(取α=β=1)的第2阶近似解和精确解的值.由表2可见,当α=β=1时,方程组(9)的近似解与准确解高度一致,比例1的近似度更高,且更稳定.本文只计算了第2阶的近似解,如果想提高近似度,可以利用变分迭代法计算更高阶的近似解. 表2 方程组(9)中当α=β=1时第2阶近似解和精确解的值Table 2 Second-order approximate and exact solutions for system (9) obtained at the values of α=β=1 综上,本文改进了校正函数,扩大了运用变分迭代法求解分数阶微分方程组的范围.在例1和例2中,只用变分迭代法计算了方程组的第2阶或第3阶近似解,数值结果表明,当α=β=1时,方程组的近似解与准确解高度一致,且稳定性较高,因此运用变分迭代法求解分数阶方程组有效、 准确. [1]WU Yongyan,WANG Chun,LIAO Shijun.Solving the One-Loop Soliton Solution of the Vakhnenko Equation by Means of the Homotopy Analysis Method [J].Chaos,Solitons & Fractals,2004,23(5): 1733-1740. [2]SONG Lina,ZHANG Hongqing.Application of Homotopy Analysis Method to Fractional KdV-Burgers-Kuramoto Equation [J].Phys Lett A,2007,367(1/2): 88-94. [3]Lesnic D.The Decomposition Method for Initial Value Problems [J].Appl Math Comput,2006,181(1): 206-213. [4]Jafari H,Daftardar-Gejji V.Solving a System of Nonlinear Fractional Differential Equations Using Adomain Decomposition [J].J Comput Appl Math,2006,196(2): 644-651. [5]Odibat Z,Momani S.Modified Homotopy Perturbation Method: Application to Quadratic Riccati Differential Equation of Fractional Order [J].Chaos,Solitons & Fractals,2008,36(1): 167-174. [6]Momani S,Odibat Z.Numerical Comparison of Methods for Solving Linear Differential Equations of Fractional Order [J].Chaos,Solitons & Fractals,2007,31(5): 1248-1255. [7]代群,李辉来.一类非线性分数阶微分方程组的爆破解 [J].吉林大学学报: 理学版,2012,50(1): 1-5.(DAI Qun,LI Huilai.Blowing-up Solutions of a Type of Nonlinear System of Fractional Differential Equations [J].Journal of Jilin University: Science Edition,2012,50(1): 1-5.) [8]Odibat Z M,Shawagfeh N T.Generalized Taylor’s Formula [J].Appli Math Comput,2007,186(1): 286-293. (责任编辑: 赵立芹) SolvingSystemsofFractionalDifferentialEquationsbyVariationalIterationMethod DAI Qun1,WANG Changjia1,LI Huilai2 The authors described approximate solutions for systems of fractional differential equations by the variational iteration method,and modified the correction function.Numerical results reveal that variational iteration method is very effective and accurate for obtaining approximate solutions of systems of fractional differential equations. fractional derivative; system of equation; variational iteration method; correction function 2014-02-27. 代 群(1981—),女,汉族,博士,讲师,从事微分方程的研究,E-mail: daiqun1130@163.com.通信作者: 李辉来(1962—),男,汉族,博士,教授,博士生导师,从事微分方程的研究,E-mail: lihuilai@mail.jlu.edu.cn. 国家自然科学基金(批准号: 11326078). O175.1 A 1671-5489(2014)05-0901-05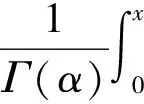

1 变分迭代法

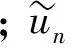
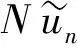

2 数值实验

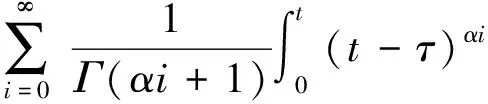



(1.CollegeofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China;
2.CollegeofMathematics,JilinUniversity,Changchun130012,China)
