矩阵的秩与非零特征值个数差的确定
2014-09-06吕洪斌杨忠鹏冯晓霞陈梅香梁小春
吕洪斌, 杨忠鹏, 冯晓霞, 陈梅香, 梁小春
(1.北华大学 数学与统计学院, 吉林 吉林 132013; 2.莆田学院 数学学院, 福建 莆田 351100;3.闽南师范大学 数学与统计学院, 福建 漳州 363000; 4.福州大学 数学与计算机科学学院, 福州 350108)
研究简报
矩阵的秩与非零特征值个数差的确定
吕洪斌1, 杨忠鹏2,3, 冯晓霞3, 陈梅香2, 梁小春4
(1.北华大学 数学与统计学院, 吉林 吉林 132013; 2.莆田学院 数学学院, 福建 莆田 351100;
3.闽南师范大学 数学与统计学院, 福建 漳州 363000; 4.福州大学 数学与计算机科学学院, 福州 350108)
以矩阵的Jordan标准形为工具, 给出了用矩阵方幂的秩表示的矩阵的秩和非零特征值个数差的确定方法, 其结果不依赖于矩阵的Jordan标准形.
矩阵秩; 矩阵方幂; 矩阵指数; 幂零矩阵
秩与非零特征值个数相等的矩阵在数理统计、试验设计、多元统计分析、金融计量统计和经济统计分析等领域应用广泛.矩阵的Jordan标准形和其初等因子是互为确定的, 因此目前已有关于矩阵的秩和非零特征值个数关系的研究结果都依赖于矩阵的Jordan标准形[1-11].本文给出矩阵的秩和非零特征值个数差的确定方法, 得到的结果不依赖于矩阵的Jordan标准形, 而以矩阵方幂的秩为基本工具.文献[2]从矩阵Jordan标准形出发, 得到:
命题1[2]设A∈n×n, 如果A的Jordan标准形中共有t个阶数分别为n1,n2,…,nt的幂零Jordan块, 则0≤r(A)-u(A)=n1+n2+…+nt-t≤n-1.
1 预备知识
参照文献[2-3], 当A∈n×n时, 总设

其中:P∈n×n可逆;
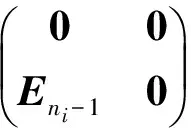
Jj=λjEnj+Nnj∈nj×nj,λj≠0,j=t+1,t+2,…,s(3)
约定当ni=1时Ji是1阶的, 因此1阶幂零Jordan块可记为N1(=0)∈; 当t=0时,ni=0,i=1,2,…,t; 显然n.由文献[1]或文献[2]中引理3知k=n1=indA, 因此式(1)中幂零Jordan块的不同阶数最多有k=n1=indA个.当A∈n×n且k=indA时, 总设

其中di∈(i=1,2,…,k)为幂零Jordan块不同阶数的个数, 显然d1+d2+…+dk=t.
易得下述引理.
引理1设A∈n×n, 则:
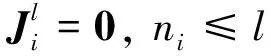
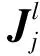
引理2设A∈n×n, 则:
1) indA=0 ⟺A可逆, 即r(A0)=r(Am)=n, ∀m∈;
2) 1≤indA=k=n1⟺ 存在1≤k≤m∈, 使得r(Ak-1)>r(Ak)=r(Am).
引理2表明indA即为JA中幂零Jordan块的最大阶数, 从而对幂零矩阵应用引理2即可得文献[4]中命题2.5; 引理2中的2)表明可不依赖Jordan标准形而只使用矩阵方幂的秩也可以确定矩阵的指数.
引理3设A∈n×n, 则:
1) 如果存在1≤l≤n-1, 使得r(Al)≠r(Al+1), 则l 2) 当r(Al)=r(Al+1)时, 则indA≤l; 3) 当1≤k=indA时,r(A)>r(A2)>…>r(Ak-1)>r(Ak)=r(Am),k≤m. 文献[9]证明了当A∈n×n为n-幂零矩阵时,r(Al)=n-l(l=1,2,…,n).实际上, 由An=0且An-1≠0即A∈Wn和引理2中2)知,n-1 引理4设A∈n×n,mA(x)=xkh(x),h(x)∈[x]且h(0)≠0, 则indA=k. 引理5设A∈n×n, 则A∈Wn⟺u(A)=0. 引理6设A∈Wn, 则A为k-幂零的 ⟺ indA=k. 定理1设A∈n×n, 如果indA=k, 则: 证明: 当indA=k=0时, 由引理2中1)知式(7)成立, 因此只证明r(A)≤n-1的情形. 由引理2及r(A)≤n-1知, 1≤t且r(Am)=r(Ak) 又由式(1),(4)知d1k+d2(k-1)+…+2dk-1+dk=n1+n2+…+nt, 再由式(5),(6),(9)知 从而由命题3可知式(7)成立. 当1≤l≤k=indA时, 由式(1)~(6),(9)有 即 再由式(4),(10)有 即 又由r(A0)=r(E)=n=kd1+(k-1)d2+…+2dk-1+dk+r(Ak)和式(7)有 r(A0)-r(A)=n-r(A)=d1+d2+…+dk-1+dk=t, 可见式(11)对l=1也成立, 即 令k-l+1=f, 则l=k-f+1, 进而可得式(12)的等价形式 又由式(13)有dl=(r(Ak-l)-r(Ak-l+1))-(r(Ak-l+1)-r(Ak-l+2)), 即式(8)成立.证毕. 式(8)表明只用矩阵方幂的秩就可得到由式(7)确定的矩阵的秩和非零特征值个数的差. 如果indA=k,A∈n×n, 则有唯一的X满足XAX=X,AX=XA,Ak+1X=Ak,X=AD称为A的Drazin逆[5].由A的Drazin逆的唯一性知下述结论成立: 推论1设A∈n×n, 当存在k(≥1)∈, 使得r(Ak-1)>r(Ak)=r(Am),k≤m时, 则在式(1)~(3)下, 有 推论1在应用上比文献[1]中定理2.5及文献[6]中定理2.1.2更方便些. 定理2设A∈n×n, 则下述条件等价: 1)r(A)=u(A); 2)A可逆或属于零特征值的Jordan块的阶数都等于1; 3) indA=0或1且d1=n-r(A); 4)mA(x)=h(x)或mA(x)=xh(x)且h(0)≠0; 5)r(A)=r(A2); 6) 对任意的m(≥2)∈, 都有r(A)=r(Am). 证明: 1)⟹2).由式(7),(9)知indA=k, 即r(A)=r(Ak).由引理3中2)知indA≤1; 当indA=0时, 由引理2中1)知A可逆; 当indA=1时, 由引理2中2)得n1=indA=1, 即A属于零特征值的Jordan块的阶数都等于1. 2)⟹3).当A可逆时, 由引理2中1)知indA=0且d1=0=n-r(A); 当A属于零特征值的Jordan块的阶数都等于1时, 由引理2中2)得indA=n1=1, 再由式(8)得,d1=r(A0)-2r(A)+r(A2)=n-r(A). 3)⟹4).由引理2和引理4可得结论. 4)⟹5).由引理2和引理4知indA=n1≤1, 再由引理2得r(A)=r(A2). 5)⟹6).由r(A)=r(A2)和引理3中2)得indA≤1, 于是由引理2知, 对任意的m(≥2)∈, 都有r(A)=r(Am). 6)⟹1).由m≥2任意性知r(A)=r(A2), 从而由引理3中2)得indA=k=0或1, 进而由式(7),(9)得r(A)-u(A)=r(A)-r(Ak)=0.证毕. 定理2简化了文献[2]中定理3的证明. 如果AA#A=A,A#AA#=A#,AA#=A#A, 则称A∈n×n是群可逆的,A#为A的群逆, 此时也称A为GP矩阵.由文献[6-8]知, 不是每个矩阵都为群可逆的, 当然GP矩阵的群逆是唯一的.由文献[7]中推论5.5.9知,A为GP矩阵 ⟺ indA≤1, 从而定理2给出了GP矩阵的等价刻画. 定理3设A∈n×n,n≥2, 则下述结论等价: 1)r(A)-u(A)=n-1; 2)r(A)=n-1,A∈Wn; 3) indA=n,JA=Nn; 4)mA(x)=xn; 5)An-1≠0,An=0; 6)r(Al)=n-l, 1≤l≤n-1且r(Al)=0,n≤l; 7) 对任意的1≤p,l≤n(p≠l), 总有r(Ap)≠r(Al). 证明: 1)⟹2)显然. 2)⟹3).由A∈Wn和引理5知u(A)=0且n1+n2+…+nt=n, 再由式(7)得 r(A)-u(A)=r(A)-r(Ak)=r(A)=n-t=n-1, 知t=1, 进而由引理2知indA=k=n1=n, 即JA=Nn. 3)⟹4).由引理2和引理4知此时mA(x)=xn. 4)⟹5).由mA(x)=xn和引理4知indA=n1=n, 进而JA=Nn, 再由式(1),(5)得An-1≠0,An=0. 5)⟹6).由An-1≠0,An=0, 引理2和引理5知indA=n,u(A)=0; 又由引理3中3)知n-1≥r(A)>r(A2)>…>r(An-1)≥1且r(An)=0, 表明r(Al)=n-l, 1≤l≤n-1且r(Al)=0,n≤l. 6)⟹7)显然. 7)⟹1).由对1≤p,l≤n(p≠l)总有r(Ap)≠r(Al)知,n-1≥r(A)>r(A2)>…>r(An-1)>r(An)≥0, 表明r(Al)=n-l, 1≤l≤n-1且r(An)=0; 又由引理5知u(A)=0, 进而由式(7)知n-1=r(A)-u(A)=r(A). 证毕. 定理3推广并简化了文献[2]中定理5的相关结论.由定理1~定理3可得: 定理4设A∈n×n, 则: 1)r(A)=u(A) ⟺r(A)=r(A2); 2)r(A)-u(A)=n-1 ⟺r(A)=n-1,r(An)=0 ⟺ indA=n,JA=Nn⟺A为n-幂零的. 定理5设A∈Wn, 则: 1) 如果存在k-1∈, 使得r(Ak-1)=1, 则indA=k, 即A为k-幂零的; 2)dl=r(Ak-l)-2r(Ak-l+1)+r(Ak-l+2),d1=r(Ak-1), 1≤l≤k=indA. 证明: 当r(Ak-1)=1时, 如果0≠r(Ak)≤r(Ak-1)=1, 则r(Ak)=r(Ak-1)=1.由引理3中2)知indA≤k-1, 再由引理6得Ak-1=0, 矛盾; 表明r(Ak)=0, 因此由引理6知indA=k, 即A为k-幂零的. 由式(8)可得2).证毕. 定理6设A∈Wn, 若存在1≤k∈, 使得r(Ak+1)=r(Ak) 由矩阵相似的充要条件为它们有相同的Jordan标准形及定理5和定理6得: 定理7设A,B∈Wn, 则: 1)A,B相似 ⟺r(Al)=r(Bl), 1≤l≤n-1; 2) 如果1≤k=indA, 则A,B相似 ⟺r(Al)=r(Bl), 1≤l≤k. 文献[9-11]讨论了3-幂零矩阵, 于是由引理6、定理5~定理7, 有: 推论2设A,B∈Wn都是3-幂零的, 则: 1)A,B相似 ⟺r(A)=r(B),r(A2)=r(B2); 2) 当A,B相似时,d1=r(A2),d2=r(A)-2r(A2),d3=n-2r(A)+r(A2), 且 [1]Nikuie M, Mirnia M K, Mahmoudi Y.Some Results about the Index of Matrix and Drazin Inverse [J].Mathematical Sciences, 2010, 4(3): 283-294. [2]梁小春, 陈梅香, 杨忠鹏, 等.矩阵的秩和非零特征值个数关系的进一步讨论 [J].闽南师范大学学报: 自然科学版, 2014(2): 1-6.(LIANG Xiaochun, CHEN Meixiang, YANG Zhongpeng, et al.Some Further Discussions on the Relationship between Ranks and Numbers of Non-zero Eigenvalues of Matrices [J].Journal of Minnan Normal University: Natural Science, 2014(2): 1-6.) [3]CHEN Meixiang, LÜ Hongbin, FENG Xiaoxia, et al.The Essential (m,l)-Idempotent Matrix and Its Minimal Polynomial [J].International Journal of Applied Mathematics and Statistics, 2013, 41(11): 31-41. [4]WU Yan, Linder D F.On the Eigenstructures of Functionalk-Potent Matrices and Their Integral Forms [J].WSEAS Transactions on Mathematics, 2010, 9(4): 244-253. [5]Bernstein D S.Matrix Mathematics Theory, Facts, and Formulas [M].2nd ed.Princeton: Princeton University Press, 2009. [6]WANG Guorong, WEI Yimin, QIAO Sanzheng.Generalized Inverse: Theory and Computations [M].Beijing: Science Press, 2004. [7]ZHANG Fuzhen.Matrix Theory: Basic Results and Techniques [M].2nd ed.New York: Springer-Verlag, 1999. [8]Baksalary O M, Trenkler G.Onk-Potent Matrices [J].Electronic Journal of Linear Algebra, 2013, 26: 446-470. [9]李殿龙.3-幂零矩阵的Jordan标准型在GLn(F)共轭作用下的迷向子群 [J].数学的实践与认识, 2008, 38(8): 143-146.(LI Dianlong.Isotropy Subgroups of Jordan Normal Form of 3-Nilpotent Matrices under the Conjugate Action ofGLn(F) [J].Mathematics in Practice and Theory, 2008, 38(8): 143-146.) [10]林荣珍, 江飞.3-幂零矩阵的相似等价类的计数 [J].数学研究, 2006, 39(4): 394-400.(LIN Rongzhen, JIANG Fei.The Enumeration of Equivalence Class of 3-Nilpotent Matrices [J].Journal of Mathematical Study, 2006, 39(4): 394-400.) [11]曾月迪, 林丽芳.3-幂零矩阵Jordan规范型的计数 [J].莆田学院学报, 2013, 20(5): 5-8.(ZENG Yuedi, LIN Lifang.The Enumeration of Jordan’s Normal Form of 3-Nilpotent Matrices [J].Journal of Putian University, 2013, 20(5): 5-8.) DeterminationofDifferencebetweentheRankandtheNumberofNon-zeroEigenvaluesofaMatrix LÜ Hongbin1, YANG Zhongpeng2,3, FENG Xiaoxia3, CHEN Meixiang2, LIANG Xiaochun4 Taking the Jordan canonical form as a basic tool, we showed the determination method of the difference between the rank of matrix’s power and the number of non-zero eigenvalues, with its result independent of the Jordan canonical form. rank of a matrix; matrix power; matrix index; nilpotent matrix 2014-05-21. 吕洪斌(1964—), 男, 汉族, 博士, 教授, 从事数值代数和矩阵理论及其应用的研究, E-mail: lhb1964@126.com.通信作者: 杨忠鹏(1947—), 男, 汉族, 教授, 从事矩阵及其应用的研究, E-mail: yangzhongpeng@126.com. 吉林省教育厅科学技术研究项目(批准号: 2013192)、福建省教育厅科研基金(批准号: JA12286; JA08196)、福建省自然科学基金(批准号: 2010J01018)和2008年福建省高校服务海西建设重点项目(批准号: 2008HX03). O151.21 A 1671-5489(2014)06-1210-05 10.13413/j.cnki.jdxblxb.2014.06.20 赵立芹)2 主要结果






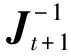
3 幂零矩阵Jordan标准形的确定
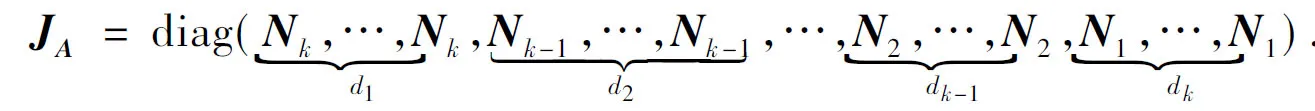
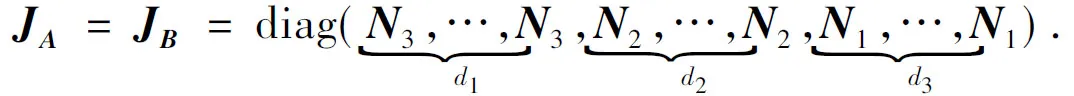
(1.SchoolofMathematicsandStatistics,BeihuaUniversity,Jilin132013,JilinProvince,China;
2.SchoolofMathematics,PutianUniversity,Putian351100,FujianProvince,China;
3.SchoolofMathematicsandStatistics,MinnanNormalUniversity,Zhangzhou363000,FujianProvince,China;
4.CollegeofMathematicsandComputerScience,FuzhouUniversity,Fuzhou350108,China)
