线性扰动随机SI系统的渐近行为

孙 艳, 刘振文, 赵亚男, 姜志侠, 谭海军

(1.长春理工大学 理学院, 长春 130022; 2.长春大学 应用数学系, 长春130022)

线性扰动随机SI系统的渐近行为

孙 艳1, 刘振文1, 赵亚男2, 姜志侠1, 谭海军1

(1.长春理工大学 理学院, 长春 130022; 2.长春大学 应用数学系, 长春130022)

用Laypunov泛函方法研究随机SI系统全局正解的存在唯一性、持久性或灭绝性以及在某些条件下的随机渐近行为.结果表明: 随机SI系统具有平稳分布, 体现了遍历性.

It公式; Lyapunov法; 正解存在唯一性; 持久性; 灭绝性; 平稳分布; 遍历性

0 引 言

由于各种传染病频繁发生, 因此生态流行病学受到人们广泛关注.Kermack等[1]给出了经典的SIR模型; 文献[2-4]研究了一些确定性生态流行病系统的性质.但种群系统和传染病系统经常受各种随机干扰的影响, 如神经系统的随机扰动、外界环境的随机干扰以及基因的随机变化等.因此, 研究随机扰动如何影响种群系统和流行病系统具有重要意义[5-14].

考虑确定性SI模型:

在随机干扰下, 系统(1)受环境白噪声的影响.本文对系统(1)进行线性扰动, 考虑系统:

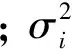
1 系统(2)的随机渐近行为

1.1系统(2)正解的存在唯一性

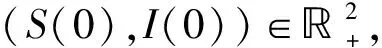
证明: 对t≥0, 系统

的初值为

u(0)=logS(0),v(0)=logI(0).

显然, 方程(3)的系数满足局部Lipschitz条件, 从而在t∈[0,τe)上存在唯一的局部解(u(t),v(t)), 这里τe为爆破时间[6].由It公式易得S(t)=eu(t),I(t)=ev(t)是系统(2)满足初始条件(S(0),的唯一局部正解.

下面将证明该解是几乎必然全局的, 只需证明τe=∞几乎必然成立即可.选取充分大的k0≥0, 使S(0),I(0)全部位于区间[1/k0,k0]内, 且对任意整数k≥k0, 定义停时

τk=inf{t∈[0,τe): min{S(t),I(t)}≤1/k, max{S(t),I(t)}≥k}.

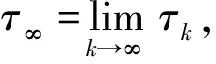
由于对任意的u>0有

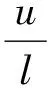
dV′=LV′dt+σ[-(S-a′)I+k′(I-b′)S]dB(t),

其中

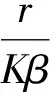
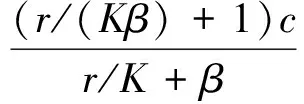
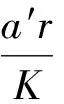
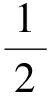
从而

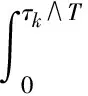
于是

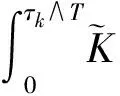
当k≥k1时, 令Ωk={τk≤T}.由式(4)有P(Ωk)≥ε.由于ω∈Ωk, 在S(τk,ω),I(τk,ω)中至少有一个达到k或1/k, 因此

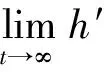
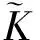
这里1Ωk(ω)是Ωk上的示性函数.令k→∞, 则

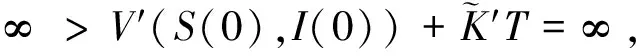
矛盾, 从而τ∞=∞几乎必然成立.

1.2系统(2)的灭绝性和持久性

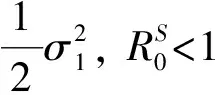
证明: 由随机比较定理, 有

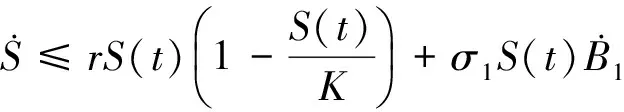
令S≤X, 其中X为方程

将式(6)两边从0到t积分, 有

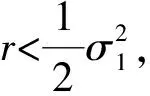
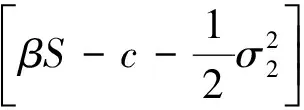
将式(7)两边从0到t积分, 有

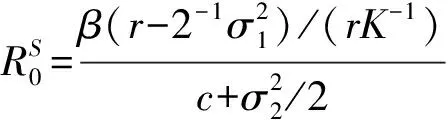
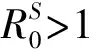
将式(8)从0到t积分, 有

且

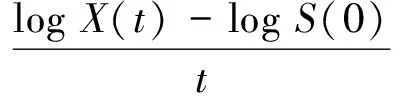
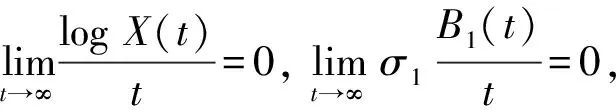
从而

于是

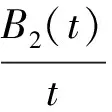
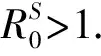
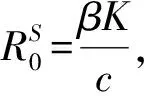
1.3系统(2)的平稳分布

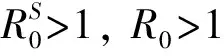
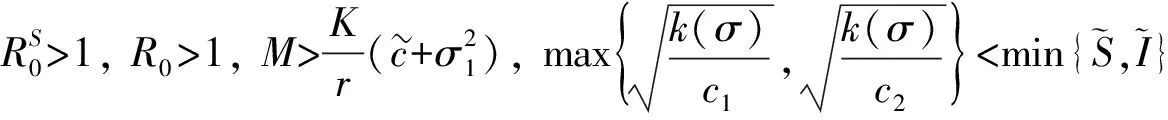
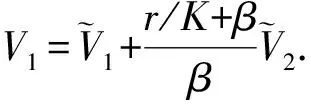
其中:

从而

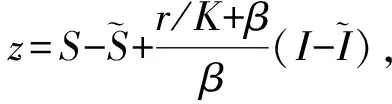
其中

因此

其中

再令V=MV1+V2(M>0), 则有

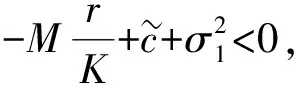
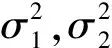
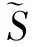
其中

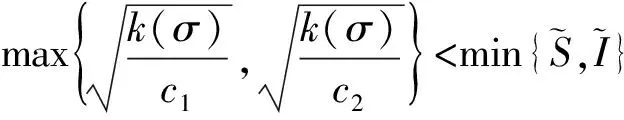
进一步, 由定理3的证明可得: 若令

在定理3成立的条件下, 可得如下结论:

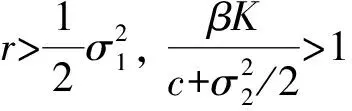
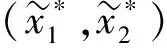
[1]Kermack W O, McKendrick A G.Contributions to the Mathematical Theory of Epidemics [J].J Hyg, 1939, 39(3): 271-288.

[2]Hethcote H W.A Thousand and One Epidemic Models [C]//Lecture Notes in Biomatemaics.New York: Springer-Verlag, 1994: 504-515.

[3]Anderso R M, May R M.Infectious Disease of Humans: Dynamics and Control [M].London: Oxford Science Publications, 1991.

[4]MAO Xuerong.Stochastic Differential Equations and Applications [M].New York: Horwood Publishing Limited, 1997.

[5]JI Chunyan, JIANG Daqing, LI Xiaoyue.Qualitative Analysis of a Stochastic Ratio-Dependent Predator-Prey System [J].J Comput Appl Math, 2011, 235(5): 1326-1341.

[6]JI Chunyan, JIANG Daqing, SHI Ningzhong.A Note on a Predator-Prey Model with Modified Leslie-Gower and Holling-Type Ⅱ Schemes with Stochastic Perturbation [J].J Math Anal Appl, 2011, 377(1): 435-440.

[7]JI Chunyan, JIANG Daqing.Dynamics of a Stochastic Density Dependent Predator-Prey System with Beddington-DeAngelis Functional Response [J].J Math Anal Appl, 2011, 381(1): 441-453.

[8]JI Chunyan, JIANG Daqing, LIU Hong, et al.Existence, Uniqueness and Ergodicity of Positive Solution of Mutualism System with Stochastic Perturbation [J/OL].Math Probl Eng, 2010-06-15.http://dx.doi.org/10.1155/2010/684926.

[9]JI Chunyan, JIANG Daqing, SHI Ningzhong.Analysis of a Predator-Prey Model with Modified Leslie-Gower and Holling-Type Ⅱ Schemes with Stochastic Perturbationc [J].J Math Anal Appl, 2009, 359(2): 482-498.

[10]JIANG Daqing, ZHANG Baoxue, WANG Dehui, et al.Existence, Uniqueness and Global Attractivity of Positive Solutions and MLE of the Parameters to the Logistic Equation with Random Perturbation [J].Sci China: Ser A, 2007, 50(7): 977-986.

[11]JI Chunyan, JIANG Daqing, SHI Ningzhong.MultigroupSIREpidemic Model with Stochastic Perturbation [J].Physica A: Statis Mech Appl, 2011, 390(10): 1747-1762.

[12]YUAN Chengjun, JIANG Daqing, O’Regan D, et al.Stochastically Asymptotically Stability of the Multi-groupSEIRandSIRModels with Random Perturbation [J].Commun Nonlinear Sci Numer Simul, 2012, 17(6): 2501-2516.

[13]JI Chunyan, JIANG Daqing.Analysis of a Predator-Prey Model with Disease in the Prey [J].Int J Biomath, 2013, 6(3): 1350012.

[14]JI Chunyan, JIANG Daqing, YANG Qingshan, et al.Dynamics of a MultigroupSIREpidemic Model with Stochastic Perturbation [J].Automatica, 2012, 48(1): 121-131.

AsymptoticBehaviorofStochasticSISystemwithLinearPerturbation

SUN Yan1, LIU Zhenwen1, ZHAO Yanan2, JIANG Zhixia1, TAN Haijun1
(1.SchoolofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China;
2.DepartmentofAppliedMathematics,ChangchunUniversity,Changchun130022,China)

We discussed the existence and uniqueness, persistence, extinction and asymptotic behavior of the globally nonnegative solution of the stochasticSIsystem under certain conditions with Lyapunov analysis method.The stochasticSIsystem possesses stationary distributions and is ergodicity.

It’s formula; Lyapunov method; existence and uniqueness of the positive solution; permanence; extinction; stationary distribution; ergodicity

2014-07-14.

孙 艳(1964—), 女, 汉族, 副教授, 从事微分方程的研究, E-mail: suny1014@163.com.通信作者: 刘振文(1979—), 男, 汉族, 博士, 讲师, 从事随机微分方程的研究, E-mail: lzw19790115765@sina.com.

国家自然科学基金(批准号: 11371085).

O211.63

A

1671-5489(2014)06-1196-07

10.13413/j.cnki.jdxblxb.2014.06.17

赵立芹)