一类超空间上诱导映射的混沌*1

李 核

(吉林师范大学数学学院，吉林 四平 136000)

一类超空间上诱导映射的混沌*1

李 核

(吉林师范大学数学学院，吉林 四平 136000)

对底空间与其诱导的超空间映射的Devaney混沌作了探讨.运用拓扑空间的传递性、周期稠密性和弱混合性，解决了底空间映射混沌时由其诱导的超空间映射混沌的问题.

超空间；传递性；Devaney混沌;弱混合

21世纪初，国内外学者受到生产实践的启示，将超空间系统研究作为科研的主要研究方向之一.其中当数Romn Flores的成果[1]较为突出，他重点讨论了紧致系统和由该系统诱导的映射的传递性，同时研究了由其诱导的超空间系统的传递性与底空间系统的传递性的内在联系，并且指出有关混沌的基本问题：底空间系统Devaney混沌与其诱导的超空间系统Devaney混沌的关系；超空间系统Devaney混沌与底空间系统Devaney混沌的关系.这类研究可以在物种的研究中作为很好的工具使用.文献[2]证明了底空间与其诱导的超空间的混沌，笔者在此基础上对其混沌性态进行了深入研究.

1 基本概念

定义1 称f为(拓扑)传递的，如果对X的任何非空开集U，V，存在n>0，使得fn(U)∩V≠Ø.称轨道在X中稠密的点为f的传递点.

定义2 若f×f是拓扑传递的，则称f是拓扑弱混合的.

证明详见文献[3].

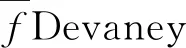
引理2[2]设X为无限点集，若f传递且周期稠密，则它必具有敏感性.

定理2 底空间系统周期稠密蕴含超空间系统也周期稠密.

2 主要结论

证明令f:I→I，为对任何x∈I，定义

引理5 下述论断等价：(ⅰ)f弱混合；(ⅱ) 对任何m≥2,fm传递;(ⅲ) 对X中任何非空开集U，V，存在n>0，使得fn(U)∩V≠Ø且fn(V)∩V≠Ø.

[2] 廖公夫，王立冬，范钦杰.映射迭代与混沌动力系统[M].北京：科学出版社，2013:104.

[3] 廖公夫,王立冬,张玉成.一类集值映射的传递性、合性与混沌[J].中国科学:A辑,2005(35):1 155-1 161.

[4] BARGE M,MARTIN J.Chaos,Periodicity and Snakelike Continua[J].Trans. Amer. Math. Soc.,1985(289):355-365.

(责任编辑 向阳洁)

ChaoticBehaviorofaClassofInducedHyperspaceMapping

LI He

(Mathematics College,Jilin Normal University，Siping 136000,Jilin China)

The bottom space and its induced hyerspace mapping of Devaney’s chaos are explored.By applying transitivity,periodic density and weak mixture of topological space,the problem of bottom induced hyperspace mapping of chaotic behavior is resolved when the bottom space is chaotic.

hyperspace;transitivity;Devaney chaos;weak mixture

1007-2985(2014)04-0017-02

2014-01-22

李 核(1987-)，女，吉林德惠人，吉林师范大学数学学院硕士研究生，主要从事拓扑动力系统研究.

O189.1

A

10.3969/j.issn.1007-2985.2014.04.004