基于曼彻斯特编码的钻井液脉冲信号提取算法

涂 兵， 李静怡， 王思成， 刘 航， 湛腾西

(1.湖南理工学院信息与通信工程学院，湖南岳阳 414006；2.复杂系统优化与控制湖南省普通高等学校重点实验室(湖南理工学院)，湖南岳阳 414006)

井下数据传输和地面数据的采集与识别是无线随钻测量的关键技术[1-2]。无线随钻测量技术在国内的应用已经非常普遍，但是噪声处理方法不完善，信号幅度较小或者噪声较强时无法对钻井液脉冲信号进行准确识别。钻井液脉冲在传输过程中受到复杂测量条件的影响，安装在井口立管处的钻井液脉冲压力传感器检测到的信号中含有大量噪声。因此，如何从频率不固定的强噪声背景下提取出微弱的钻井液脉冲信号并进行准确识别，是钻井液脉冲传输技术中的一个难题。

张恒等人[3]提出了小波变换的无线随钻系统信号提取算法；赵建辉等人[4]根据信号干扰及噪声的特点，在采用线性滤波方法还原脉冲信号的基础上，采取非线性“平顶消除”的方法对现场采集到的信号进行处理；廖琪梅等人[5]提出了一种基线漂移的矫正算法；苏义脑等人[6-7]根据曼彻斯特编码钻井液脉冲信号的特点建立了识别模型;郑一等人[8]对钻井液脉冲信号采用基于集合经验模态的降噪算法进行处理。但是，目前的算法在钻井液脉冲信号的识别和起始时刻存在识别不准确和提取不精确的问题。针对无线随钻测量中微弱钻井液脉冲信号提取与识别问题，笔者对井下曼彻斯特编码的数据传输格式进行了分析，对采集到的钻井液脉冲信号采用形态滤波算法进行去噪处理；针对去噪后的钻井液脉冲信号，提出了基于周期内16等份分割算法来提取钻井液脉冲信号的开始时刻，并将模式相识度识别算法应用到了钻井液脉冲识别上。

1 钻井液脉冲信号去噪算法研究

1.1 噪声分析

由于井下条件复杂多变，钻井液脉冲信号在传输过程中受到各种噪声的干扰，导致地面采集系统采集到的钻井液脉冲信号幅值小、噪声大。图1为采集到的一段现场钻井液压力波原始波形。从图1可以看出，钻井液压力值波动范围为0.01～0.10 MPa。图2为对图1中原始波形进行频谱分析后的示意图。从图2可以看出，采集到的钻井液脉冲信号存在有较大的高频噪声和低频噪声。因此，在提取钻井液脉冲信号前需要先对其进行去噪处理[9-10]。

图1 钻井液脉冲信号原始波形Fig.1 Original waveform of pulse signal in drilling fluids

1.2 形态滤波算法

对钻井液脉冲信号进行一维处理时，运用膨胀与腐蚀运算来设计信号的形态滤波器。夹杂在正常信号中的噪声可以视为是由“尖峰”和“波谷”组成的，数学形态学理论认为：由腐蚀与膨胀组成的开运算可以消除信号的“尖峰”，闭运算则可以填充信号的“波谷”，并且开、闭运算均具有低通特征[11-12]。由于钻井液脉冲信号既具有高频特性也具有低频特性，因此能有效抑制钻井液脉冲信号中的各种噪声，具体应用时采用2种滤波器的组合平均形式,形态滤波结构如图3所示。

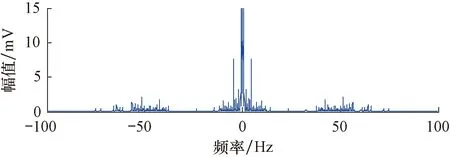
图2 信号频谱分析Fig.2 Analysis of signal spectrum

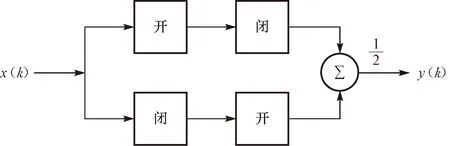
图3 形态滤波结构Fig.3 Structure of morphological filtering

设待处理信号f(n)是采样得到的一维多值信号，其定义域为D[f]={0，1，2，3，…，N}；g(x)为一维结构元素序列，其定义域为D[g]={0，1，2，3，…，P}；其中，P和N为整数。

腐蚀与膨胀运算分别定义为[11-12]:

(f⊗g)(n)=min{f(n+x)-g(x):x∈D[g]}

(n=1,2,3,…，N)

(1)

(f⊕g)(n)=max{f(n-x)+g(x):x∈D[g]}

(n=1,2,3,…，N)

(2)

式中:⊗为腐蚀运算; ⊕为膨胀运算。

由式(1)和式(2)可引出形态学开运算、 闭运算的定义,分别为:

(f∘g)(n)=(f⊗g⊕g)(n)

(3)

(f·g)(n)=(f⊕g⊗g)(n)

(4)

式中：∘为开运算符号；·为闭运算符号。

设钻井液脉冲输入信号为x(k)=s(k)+n(k)，(k=1，2，…，N)，其中s(k)为原始信号，n(k)为噪声，则滤波输出信号为：

(5)

其中OC[x(n)]=(x∘g·g)(n)

(6)

CO[x(n)]=(x·g∘g)(n)

(7)

为了能够同时消除泵冲基值的漂移和钻井液脉冲信号的高频噪声，需要设计不同长度的结构元素组成2组形态滤波，滤除钻井液脉冲信号噪声,流程如图4所示：第一组形态滤波滤去基线漂移，形态滤波算法中g(n)采用方波信号，所选结构元素的长度至少应大于基线漂移的波形长度，实验中选取结构原素长度为200，g(n)=1,g(100+n)=0,n=(1，2,…，100)；第二组形态滤波滤去高频噪声，所选结构元素的长度较小，实际选取结构原素长度为50，g(n)=1,g(25+n)=0,n=(1，2,…，25)。图5为消除高频噪声和泵冲基值后的波形，从图5可以看出，信号的噪声得到有效消除。

图4 钻井液脉冲信号去噪流程Fig.4 Flow chart of denoising for pulse signal in drilling fluids

图5 钻井液脉冲信号噪声消除Fig.5 Pulse signal denoising in drilling fluids

2 钻井液脉冲信号提取算法

2.1 基于等份分割的初步时刻分辨算法

钻井液脉冲信号进行去噪处理后，地面解码系统对采集到的钻井液脉冲信号进行解码时，如果钻井液脉冲信号开始时刻分辨不准确，会导致解码误码率的增大。因此，如何准确确定钻井液脉冲信号的开始时刻，是正确解码时的一个关键问题。

对曼彻斯特编码的井下信号发出的数据格式进行分析发现：井下仪器开始启动后，会发送出一连串二进制编码为“1”的数据，反映到立管压力波上的压力，则变换为一连串重复性好的波形信号，可以利用这一连串重复性好的钻井液脉冲波形进行开始时刻的初步捕捉。以传输速率0.5 bit/s的曼彻斯特编码钻井液脉冲为例，算法步骤如下：

1) 将经过去噪处理后的钻井液脉冲信号在一个周期内分成16等份，采样频率为200 Hz，每等份采样的点数为25，把16等份点各自区间中的数据进行求和。

设一个周期内钻井液脉冲信号数据x=(1，2，3，…，399，400)。x周期内的采样值划分为16等份，每等份的数学表达式为：

图6中A点为需要提取的钻井液脉冲信号的开始时刻。通过计算y(x)<0，y(x+1)>0的位置，即图6中B点所在位置为符合y(x)<0，y(x+1)>0条件的点。

图6 钻井液脉冲信号时间点的初步捕捉算法Fig.6 Preliminary capture and algorithm of time point for pulse signal in drilling fluids

2) 图7中y(12)<0，y(13)>0，即y(12)为B点位置：根据B点在步骤1)中划分的等份位置，可以初步判断出A点时刻所在位置。

设数据传输比特率为0.5 bit/s，钻井液脉冲信号采用频率为200 Hz，采用16等份提取钻井液脉冲信号初始时刻位置，区域分辨率为2/16=0.125 s，采用模式相识度波形识别算法,在一个数据编组内能对钻井液脉冲信号进行准确识别。

图7 计算的各等份分割值Fig.7 Calculation of signal value for each equal segment

2.2 钻井液脉冲信号识别模型建立

曼彻斯特编码的规则是：在一个比特周期内，信号由高电平到低电平代表的数据位为“1”，相反则为“0”。井下DSP对数据进行曼彻斯特编码时，如果存在连续的“11”或者“00”时，表示钻井液脉冲波形在一个比特周期内有连续上升或者连续下降波形，连续上升波形识别为“1”，相反则为“0”。采用2比特周期内的钻井液压力波进行波形识别时，波形存在有8种形状特征，对应的二进制编码值为00～11。图8为分别对8种形状进行二进制编码的结果。

图8 建立的识别模型Fig.8 Establishment of recognition model

2.3 基于模式相似度的波形识别算法

模式相似度研究的是类与类之间的相似性测度问题。判断样品之间的相似性常采用的是近邻准则，将待分类样品与模型样板进行比较，从而确定待测试样品的分类。

在建立了如图8所示的识别模型后，波形识别采用模式相似性测度方法。根据建立的识别数学模型，设识别数学模型特征向量为Xi=(xi1,xi2,…,xin)T、经过去噪处理和基值调整后的实时采样钻井液脉冲特征向量为Xj=(xj1,xj2,…，xjn)T。

模式相似性度算法公式为[12-15]：

(13)

对图9所示的钻井液脉冲信号进行模式相似度计算，计算结果如图10所示，可以看出第8号波形模型与参考模型存在一个最大值，从而可以把钻井液脉冲信号识别出来。

图9 识别波形Fig.9 Recognition of waveform

图10 模式相似度识别算法Fig.10 Algorithm and recognition with pattern similarity

3 现场试验

该算法在华北油田某井进行了现场试验。试验目标井深3 000 m，钻井液黏度为10 mPa·s，从井深2 000 m开始进行定向测量。为了验证提取算法的可靠性和解码正确率，进行试验时同时利用一台Haliburton地面解码系统对采集的钻井液脉冲信号进行处理和解码。对解码出来的比特流数据进行对比分析，可以看出，笔者提出的钻井液脉冲信号识别算法能对曼彻斯特编码的钻井液脉冲信号进行有效提取，误码率低于1.5%(见表1)。

表1油田现场钻井液脉冲信号解码结果

Table1Decodingresultsofpulsesignalsindrillingfluidsatwellsite

序号解码物理量Sperry_Sum解码值本文算法解码值1INC45.345.262INC45.945.873AZ68.268.104AZ69.368.755GTF183.2183.256GTF183.4183.277BTF57.257.158BTF56.957.10

Speery_Sum公司的解码数据精确到小数点后1位，笔者提出的识别算法根据解码出来的比特流得到的工程数据精确到小数点后2位，精度更高。

4 结 论

1) 通过分析钻井液脉冲信号的噪声特点，提出了形态滤波去噪算法，能够对噪声进行有效去除，能更精确地提取钻井液信号,并根据钻井液脉冲信号的编码特点建立了2比特识别周期内的数学模型，提出了模式相似度的波形识别算法，能对钻井液脉冲信号进行准确识别，解出数据比特流。

2) 在进行去噪时也存在着部分有用信号被消除、识别正确率受到起始时刻以及有用信号幅值大小的影响，提出的去噪和识别算法还不够完善。针对这些问题，将深入开展钻井液脉冲信号起始时刻提取和识别算法的研究，重点研究解决起始时刻高分辨和信号微弱波动识别问题。

参考文献
References

[1] 刘修善，苏义脑.地面信号下传系统的方案设计[J].石油学报，2000，21(6):88-90.

Liu Xiushan，Su Yinao.Scheme design of downward signaling system[J].Acta Petrolei Sinica，2000，21(6):88-90.

[2] Zhao Jianhui，Wang Liyan，Li Fan.An effective approach for the noise removal of mud pulse telemetry system[C]∥The Eighth International Conference on Electronic Measurement and Instrumnets.Electronic Measurement and Instruments,2007,ICEMI’07，8th International Conference,July 18-August 16,Xi’an.2007:971-974.

[3] 张恒，李安宗，李传伟.基于离散平稳小波变换的无线随钻系统测试信号处理[J].石油钻探技术，2007，35(2)：49-51.

Zhang Heng,Li Anzong,Li Chuanwei.Signal processing of wireless measurement while drilling based on discrete stationary wavelet transform[J].Petroleum Drilling Techniques，2007，35(2)：49-51.

[4] 赵建辉，王丽艳，盛利民，等.去除随钻测量信号中噪声及干扰的新方法[J].石油学报，2008，29(4):596-600.

Zhao Jianhui,Wang Liyan,Sheng Limin,et al.Anonlinear method for filtering noise and interference of pulse signal in measurement while drilling[J].Acta Petrolei Sinica,2008,29(4):596-600.

[5] 廖琪梅，李安宗，屈景辉，等.随钻测井钻井液脉冲信号基线漂移的矫正[J].石油钻采工艺，2008，30(4)：41-43.

Liao Qimei，Li Anzong，Qu Jinghui，et al.Mud signal baseline drift rectification in mearsurement while drilling[J].Oil Drilling & Production Technology，2008，30(4):41-43.

[6] 涂兵，李德胜，林恩怀.基于聚类算法的MWD泥浆脉冲信号识别研究[J].传感技术学报，2012，25(8)：1172-1176.

Tu Bing，Li Desheng，Lin Enhuai.Research on MWD mud pulse signal recognition based on clustering algorithm[J].Chinese Journal of Sensors and Actuators，2012,25(8):1172-1176.

[7] 苏义脑，盛利民，王家进，等.一种接收和检测泥浆压力波信号的方法与装置:中国，CN1657740A[P].2004-02-16.

Su Yinao，Sheng Limin，Wang Jiajin，et al.A method of receiving and detecting mud pressure wave signal:China,CN1657740A[P].2004-02-16.

[8] 郑一，孙晓峰，陈健，等.基于集合经验模态的随钻脉冲信号优良降噪算法[J].石油勘探与开发，2012，39(6)：750-753.

Zheng Yi，Sun Xiaofeng，Chen Jian，et al.Extracting pulse signals in measurement while drilling using optimum denoising methods based on the ensemble empirical mode decomposition[J].Petroleum Exploration and Development，2012,39(6):750-753.

[9] Zhao Qingjie,Zhang Baojun，Wang Wei.Data processing techniques for a wireless data transmission application via mud[J].EURASIP Journal on Advances in Signal Processing，2011,32(1)：45-51.

[10] Chen Wenyuan,Fang Bin,Wang Yi.MWD drilling mud signal De-noising and signal extraction research based on the pulse-code information：proceedings of the 2010 International Conference on Wavelet Analysis and Pattern Recognition[C].2010：244-249.

[11] 张伟，师奕兵，卢涛.无线随钻泥浆信号小波包去噪处理[J].电子测量与仪器学报，2010，24 (1):80-84.

Zhang Wei，Shi Yibing，Lu Tao.Wavelet packet de-noising method of wireless measurement while drilling[J].Journal of Electronic Measurement and Intrument，2010，24(1)：80-84.

[12] 田絮资，杨建，黄力宇.心电信号去噪的数学行态学滤波器[J].计算机工程与应用，2012,48(2):124-126.

Tian Xuzi，Yang Jian，Huang Liyu.Morphological filter to remove power-line interference and baseline wander in electro-cardiogram[J].Computer Engineering and Applications，2012,48(2)：124-126.

[13] 张建成，吴新杰.形态滤波在实时信号处理中应用的研究[J].传感技术学报，2007,20(4):828-830.

Zhang Jiancheng，Wu Xinjie.Research on applications of morphological filtering in real-time signal processing[J].Chinese Journal of Sensors and Actuators，2007，20(4):828-830.

[14] 陈平，李庆民.基于数学形态学的数字滤波设计与分析[J].中国电机工程学报，2005,25(11):60-65.

Chen Ping，Li Qingmin.Design and analysis of mathematical morphology-based digital filters[J].Proceedings of the CSEE，2005，25(11):60-65.

[15] 赵立业，李宏生，周百令，等.基于形态小波的高精度重力仪信号快速滤波算法[J].东南大学学报：自然科学版，2010,40(6):1217-1221.

Zhao Liye，Li Hongsheng，Zhou Bailing，et al.Fast filter algorithm based on morphological wavelet in precise gravimeter signal processing[J].Journal of Southeast University：Natural Science Edition，2010，40(6)：1217-1221.