网格划分对边坡稳定有限元分析的影响
2014-09-06李永亮余成华马佐成张殿义
李永亮,余成华,马佐成,张殿义
(1.长安大学 公路学院,陕西 西安 710064;2.深圳市勘察研究院有限公司,广东 深圳 518026)
网格划分对边坡稳定有限元分析的影响
李永亮1,余成华2,马佐成1,张殿义1
(1.长安大学 公路学院,陕西 西安 710064;2.深圳市勘察研究院有限公司,广东 深圳 518026)
摘要:网格划分对边坡稳定性有限元分析的准确性有很大影响,而目前对此影响的研究相对不够。以有限元强度折减法在边坡稳定性分析中的一标准算例为依据,探讨ABAQUS中网格划分技术、网格形状、网格密度、局部加密网格、网格生成算法和单元积分方法对边坡稳定性计算的影响。最后用一复杂土坡案例分析以上诸因素对边坡稳定性分析的敏感性,得出在适当范围内加密网格可节约计算时间,二次积分单元计算精度高但更耗成本等结论,对边坡稳定分析的网格划分具有一定参考价值。
关键词:ABAQUS;强度折减法;网格划分;边坡稳定性
强度折减理论概念由Zienkiwicz等(1975年)最早提出并运用于边坡的稳定性分析,之后Griffith,Dwason等对其发展做了大量工作。我国郑颖人[1-3]、赵尚毅[1-2]、宋二祥[4]、郑宏[5]等扩大了有限元强度折减法的应用范围。不同流动法则、屈服准则、计算模型的范围和计算参数对强度折减法计算精度的影响已得到大量研究[5-7],而对网格划分影响的研究相对不够。因此,探究网格划分对边坡稳定性分析的影响极有必要。
1 有限元强度折减法及边坡整体失稳的判据
边坡稳定分析的有限元强度折减法是通过不断降低岩土体抗剪切强度参数直至达到极限破坏状态为止,程序自动根据弹塑性有限元计算结果得到滑动破坏面,同时得到边坡的强度储备安全系数[8]。折减后的抗剪强度参数表达为:
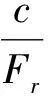
(1)
(2)
式中:c和φ是土体所能够提供的抗剪强度;cm和φm是维持平衡所需要的或土体实际发挥的抗剪强度;Fr是强度折减系数。ABAQUS通过将Fr定义为场变量,初始分析时为避免模型破坏,可取Fr<1,在后续分析步中线性增加场变量Fr,在坡体达到临界状态以前,每个折减系数对应着一个塑性区发展状况,计算中止(数值不收敛)后按照失稳评价标准确定安全系数[9]。
采用有限元法计算边坡稳定时判断边坡失稳的判据有以下几种类型[10]:
(1)以有限元计算不收敛为标准。其认为当边坡处于极限平衡状态时,非线性有限元方程组的迭代过程将不收敛(内含迭代次数或残差应力与外力比值)。
(2)以广义剪应变标准或广义塑性应变标准为标准。其认为当边坡达到极限平衡状态时,广义剪应变或广义塑性应变的等值线图中,必有一条等值线(通常是数值较小的那条等值线)由坡底贯通到坡顶。
(3)以位移为标准。如坡顶位移增量与折减系数增量之比、残差位移、无量纲位移、特征部位位移或位移的突变等。
(4)以塑性区的贯通为标准,可由塑性应变及塑性功表示。
(5)联合使用(1)~(4)中的某几条。
2 计算模型与参数
2.1力学模型和屈服准则
采用理想弹塑性本构模型,屈服准则采用Mohr-Coulomb强度准则,屈服条件为:

(3)
式中:θα为洛得应力角;I1为应力张量的第一不变量;J2为偏应力张量的第二不变量[11]。
2.2边坡模型
采用参考文献[2]中郑颖人等的一个算例,边坡模型如图1所示。

图1边坡模型图
2.3边坡模型网格划分
根据ABAQUS的网格划分技术,四边形结构化网格如图2所示。
2.4土体参数
土体的本构关系采用Mohr-Coulomb弹塑性模型,其参数见表1。
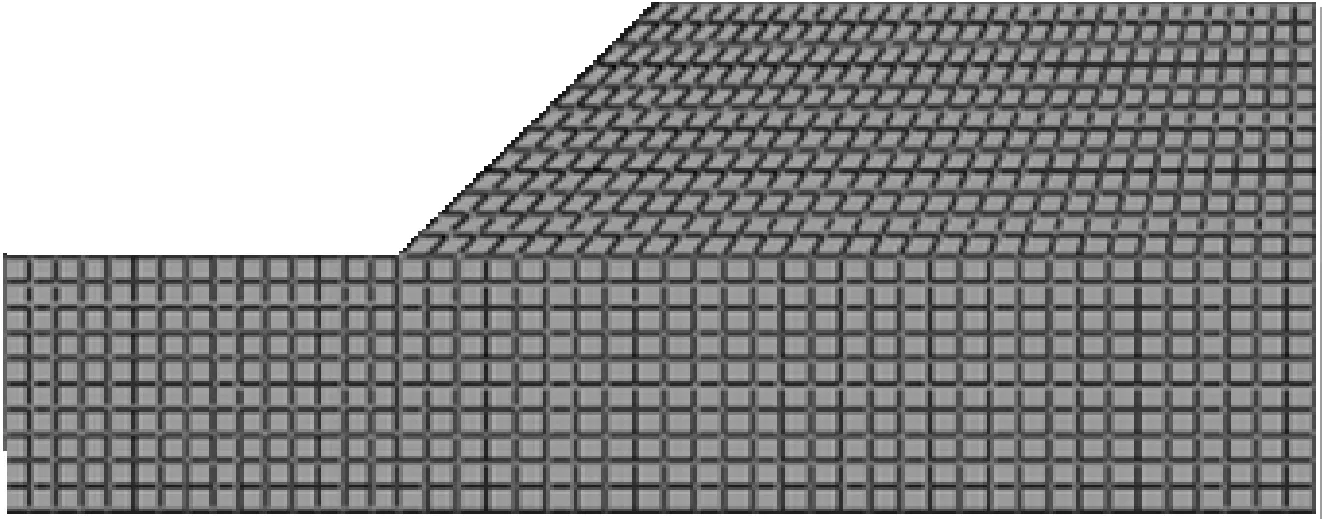
图2边坡网格划分图

表1 土体物理力学参数
3 网格划分计算及结果分析
本文所采用的边坡算例,郑颖人等得出其安全系数为1.21,Spencer法算得为1.20。以下分析网格划分对该边坡稳定性计算的影响。
3.1网格划分技术的影响
3.1.1四边形网格下不同划分技术
计算结果见表2。
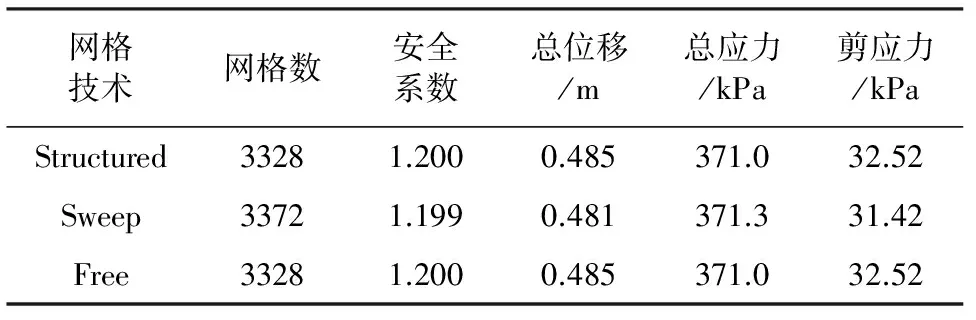
表2 四边形网格下的计算结果
注:表中网格数均是在相同的网格种子布置下而得。
Structured技术是将一些标准的单元(如四边形、正方体)等应用于一些简单的没有独立的点、线、面和洞的几何区域。Sweep技术是先在源边或面上生成网格,然后沿着扫略路径复制节点,直到目标边或面,得到网格。Free技术是最为灵活的网格划分技术,几乎可以用于任何形状[9]。
由上表可知Structured技术和Free技术划得的网格数少于Sweep技术,并且其安全系数、总位移和剪应力值均相同而较Sweep技术的结果精确一些。
3.1.2三角形网格下不同划分技术
计算结果见表3。
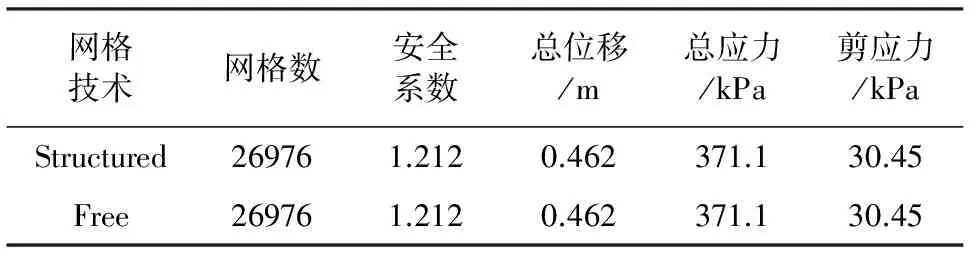
表3 三角形网格下的计算结果
由表3可知三角形网格下Structured技术和Free技术所得网格数、安全系数等值相同,此时两种划分技术所得计算精度和耗时一样。
3.2网格密度的影响
3.2.1四边形网格Structured技术下不同网格密度
计算结果见表4。

表4 四边形网格Structured技术时的计算结果
根据表4可知当网格数为3328和2726时所得的安全系数和剪应力都基本不再变化,说明网格密度已经足够[12]。网格数为2726时边坡总位移云图如图3所示。

图3网格数为2726时的总位移云图
3.2.2四边形网格Sweep技术下不同网格密度
计算结果如表5。
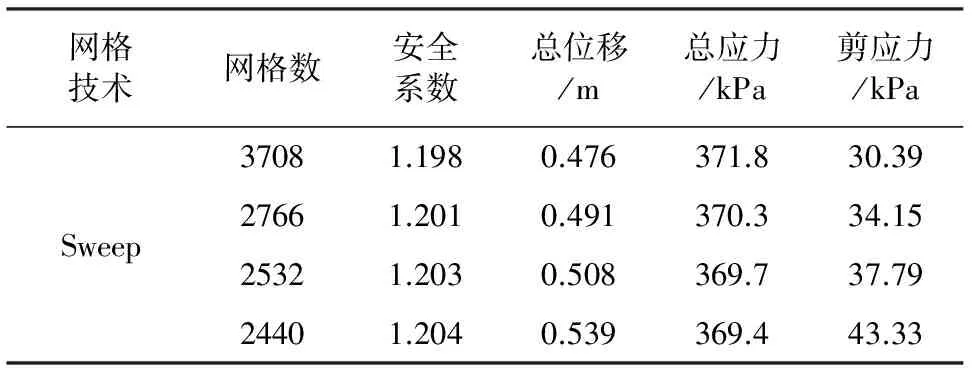
表5 四边形网格Sweep技术时的计算结果
类似于表4,当网格数为2766和2532时Fr和剪应力值变化很小,说明此时网格数目已能满足计算精度要求。将表5与表4比较可知,同样条件下Sweep技术比Structured技术划出的网格偏少而又能保证计算结果的精度且计算历时相对较小。
3.3网格形状的影响
3.3.1Structured技术下不同网格形状
计算结果见表6。由表6可知,在Structured技术下四边形网格数目最少,而计算得安全系数较其他两者精确,且其总位移和剪应力值介于后两者值之间,所以此类情况应优先考虑采用四边形形状网格。
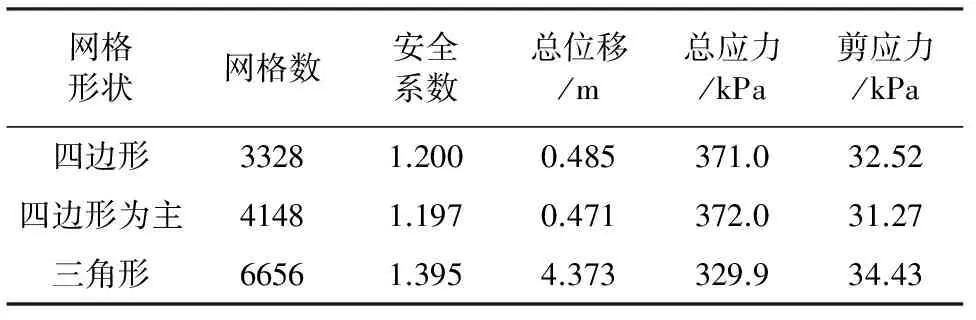
表6 Structured技术下不同网格形状计算结果
3.3.2Sweep技术下不同网格形状
计算结果见表7。

表7 Sweep技术下不同网格形状计算结果
由表7可知,这两种形状的网格此时所得的网格数、安全系数、总位移和应力值均相同。
3.4局部加密网格的影响
根据有限元计算的特点并结合该边坡模型,在坡顶之后一定范围内加密网格,计算结果见表8。
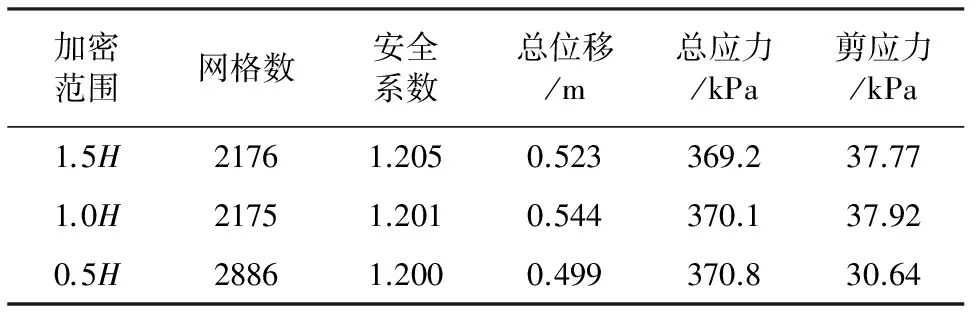
表8 网格局部加密的计算结果
注:H表示坡高,本文H=20 m。
通过表8与表4的比较可知,在1.5H和1.0H范围内加密网格,在模型其他部位划分相对稀疏的网格既能保证计算的精确性,又能减少有限元迭代计算的总次数而节约计算时间。而在0.5H范围内的加密计算结果并不理想,故建议在进行分析时可适当局部细化网格来提高计算效益。
3.5网格生成算法的影响
在Free技术下不同的网格生成方法计算结果如表9。
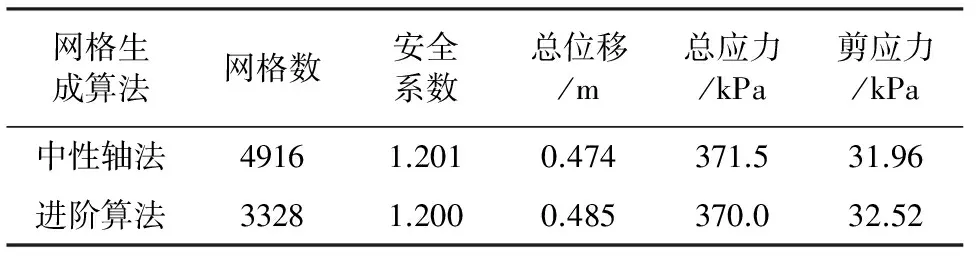
表9 不同网格生成算法的计算结果
中性轴算法生成的网格与种子吻合程度较差,进阶算法生成的网格和种子可以较好地吻合,更容易得到大小均匀的网格。由表9可知进阶算法所得安全系数和应力值等较中性轴算法精确。
3.6单元积分方法的影响
不同单元积分方法的计算结果见表10。

表10 不同单元积分方法的计算结果
由表10可知Quadratic对安全系数和应力等的计算结果较其他两种积分方法准确,但其计算耗时大。线性缩减积分限于其自身特点,所得数值不够精确。
4 案例分析
为了探究网格划分诸因素对边坡稳定性分析的敏感性,采用一复杂边坡案例对其进行分析[8]。
4.1边坡模型如图4所示。
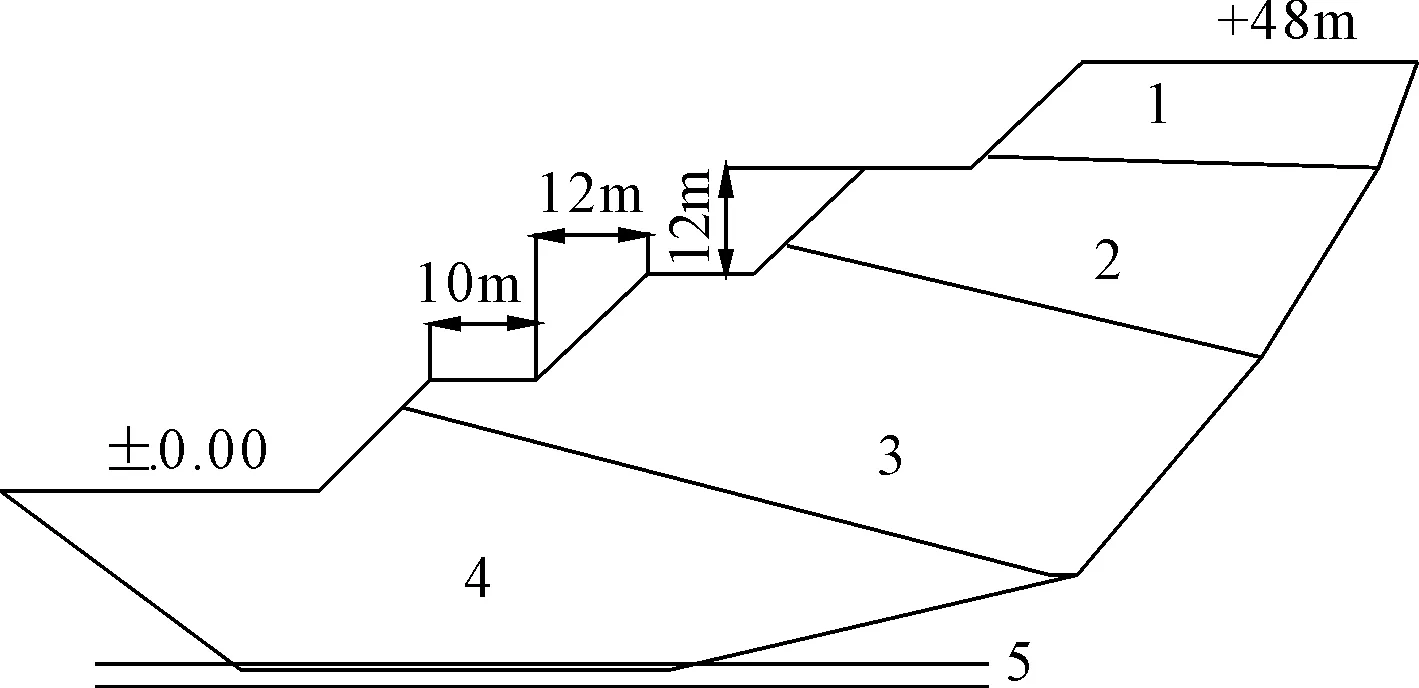
图4边坡模型图
4.2土体物理力学参数
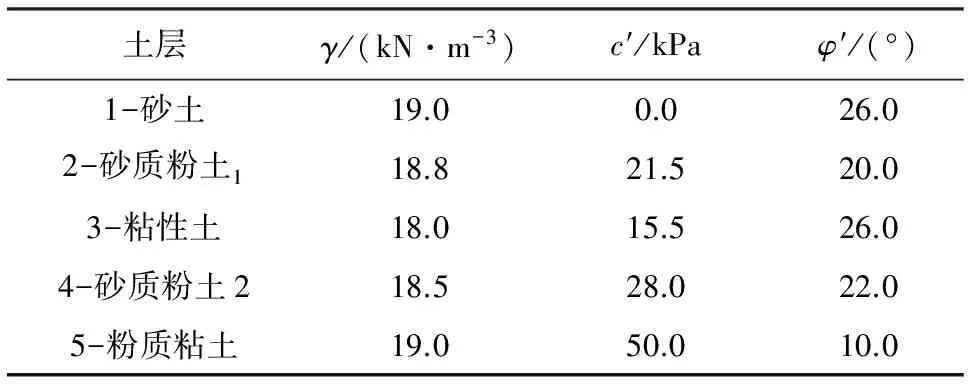
表11 土体物理力学参数
4.3不同网格划分因素下的边坡稳定性分析
计算结果见表12。由表12可知当网格形状和密度种子一定,不同的划分技术所得边坡安全系数差异很小。当网格形状和划分技术相同而网格密度不同时,分析得出的安全系数数值变化并不明显。在划分技术一定而网格形状不同时,Structured技术下三角形网格在同样的网格密度下所得结果不理想而且计算耗时多。在坡顶后适当区域内加密网格求得安全系数数值变动不大,只是起到相对节约计算成本的作用,而对计算结果的精度影响不显著。同样的网格密度下进阶算法所得安全系数相对较中性轴算法的结果准确,但若进行调整会发现二者分析得出的结果精确程度相同。不同的单元积分方法对计算结果有很大影响,二次型积分方法求得的安全系数较线性积分精确,而相同情况下缩减积分的结果明显偏大。因此,对于此边坡,网格划分诸因素中单元积分方法对边坡稳定性计算影响最大,网格形状和网格生成方法次之,最后是网格划分技术和局部区域加密网格。

表12 网格划分因素影响程度分析结果
5 结 语
采用ABAQUS探讨了不同的网格划分因素对强度折减法分析边坡稳定性的计算结果及敏感性,得出如下结论:
(1)在四边形和三角形网格下Structured技术划分的网格数相对其他技术所得网格较少,求出安全系数和应力值等的精确程度和计算时间优于Sweep技术和Free技术。
(2)在Structured技术和Sweep技术下对模型划分不同密度的网格时当求出的安全系数、最大位移和应力值等趋于稳定时说明计算结果已满足要求。实际建模中,应在保证分析精度的前提下,选择适当的网格密度,对模型进行局部网格适当细化并尽量保证单元形状是规则的。
(3)只要网格种子布置得不是过于稀疏,使用进阶算法往往更容易得到形状规则的网格,而且其结果也相对较为准确,但这不是绝对的,保证单元尺寸均匀十分重要。另外二次完全积分所得应力值和安全系数更精确,但其计算成本高,分析时应据实际情况选用最优的单元积分方法。
(4)通过复杂边坡案例对网格划分因素的敏感性分析可知,对边坡稳定性计算结果影响最大的是单元积分方法,其次为网格形状和网格生成方法次之,最后为网格划分技术和局部区域加密网格的影响。
上述结论仅是数值模拟结果,有待于在工程实践中进一步验证。
参考文献:
[1]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57-61,78.
[2]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.
[3]刘明维,郑颖人.基于有限元强度折减法确定滑坡多滑动面方法[J].岩石力学与工程学报,2006,25(8):1544-1549.
[5]郑宏,刘德富.弹塑性矩阵Dep的特性和有限元边坡稳定性分析中的极限状态标准[J].岩石力学与工程学报,2005,24(7):1099-1105.
[6]李宗坤,霍香丽,李艳.本构模型对边坡稳定有限元分析的影响[J].人民黄河,2009,31(12):89,91.
[7]李垠,苏凯,李杰.Mohr-Coulomb等面积圆屈服准则在边坡稳定性分析中的应用[J].大地测量与地球动力学,2009,29(2):135-139.
[8]郑颖人,等.边坡与滑坡工程治理(第2版)[M].北京:人民交通出版社,2010.
[9]费康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010.
[10]谢新宇,刘开富,张继发.边坡及基础工程数值分析新进展[M].北京:科学出版社,2010.
[11]张宏.应用弹塑性理论[M].西安:西北工业大学出版社,2011.
[12]曹金凤,石亦平.ABAQUS有限元分析常见问题解答[M].北京:机械工业出版社,2009.
TheEffectoftheMeshontheFEMAnalysisofSlopeStability
LI Yong-liang1,YU Cheng-hua2,MA Zuo-cheng1,ZHANG Dian-yi1
(1.SchoolofHighways,Chang’anUniversity,Xi’an,Shaanxi710064,China;2.ShenzhenInvestigation&ResearchInstituteCo.,Ltd.,Shenzhen,Guangdong518026,China)
Abstract:Meshing has great impact on the accuracy of the FEM analysis of slope stability,but its research is currently insufficient.By employing ABAQUS and on the basis of an standard calculation example of slope stability which was analyzed by FEM Shear Strength Reduction Method,the effects of meshing techniques,mesh shapes,mesh density,partially-refined mesh,mesh algorithm and element integration on account of slope stability were investigated.At last,the effects of above factors on the sensitivity of slope stability were analyzed on a complex soil slope.the results indicate that the increase of the refinement of the mesh in proper regions can reduce computing time,quadratic integration element method has higher calculation accuracy but with larger computational expense and so on.These findings have a certain reference value for the meshing of the analysis of slope stability.
Keywords:ABAQUS;shear strength reduction method;meshing;slope stability
DOI:10.3969/j.issn.1672-1144.2014.06.026
中图分类号:TU413.6+2
文献标识码:A
文章编号:1672—1144(2014)06—0133—04
作者简介:李永亮(1992—),男,甘肃天水人,硕士研究生,研究方向为边坡稳定分析、加筋边坡和加筋挡墙。
收稿日期:2014-07-18修稿日期:2014-08-21
