西藏某水电站工程首部枢纽平衡防渗优化设计
2014-09-06党发宁王振华田红梅
党发宁,熊 璐,王振华,2,田红梅
(1.西安理工大学 岩土工程研究所,陕西 西安 710048;2.中国电力工程顾问集团 西北电力设计院,陕西 西安 710075)
西藏某水电站工程首部枢纽平衡防渗优化设计
党发宁1,熊璐1,王振华1,2,田红梅1
(1.西安理工大学 岩土工程研究所,陕西 西安 710048;2.中国电力工程顾问集团 西北电力设计院,陕西 西安 710075)
摘要:以“平衡防渗原理”为依据进行防渗帷幕各分区设计,即依据渗漏量和允许水力坡降的控制标准先确定防渗帷幕的深度,再依据绕过两岸帷幕的渗流速度等于绕过坝基河床下帷幕的渗流速度确定防渗帷幕长度,最后,依据穿过帷幕的渗流速度等于绕过坝基河床下帷幕的渗流速度确定防渗帷幕的厚度,可以避免防渗帷幕局部防渗过当或防渗不足,达到全局最优。对西藏某水电站工程首部枢纽拦河坝不同防渗分区的各种防渗方案进行了平衡防渗优化设计,通过三维有限元软件的计算结果分析,验证了依据“平衡防渗原理”进行的结构优化设计的合理性。研究成果不仅对该工程防渗方案的修改提供依据,还对类似工程防渗帷幕的设计提供参考依据。
关键词:防渗帷幕;渗流速度;优化设计
水利水电工程中,防渗工程成败往往决定着工程是否能发挥预期效益。一方面取决于防渗工程的施工质量,另一方面取决于防渗工程设计是否合理。防渗帷幕的设计包括深度、长度以及厚度的设计。按照规范规定,防渗帷幕的设计应该符合以下要求:控制渗漏对坝基及两岸边坡稳定的不利影响;控制坝基软弱夹层、断裂破碎带、岩体裂隙充填物以及抗水性能差的岩层不产生管涌;控制坝基面渗透压力和渗流量;具有可靠的连续性和足够的耐久性。
国内外学者对防渗帷幕的设计进行了大量工作,杜延龄等[1]认为岩基中灌浆帷幕的防渗效果应以其相对渗透性来评价,并应采用其合理值,过分减小帷幕的渗透性是不能取得相应防渗效果的。对于透水岩基很深的情况,其帷幕深度也应采用合理值。由于灌浆帷幕本身是透水的,过分加大其深度同样不能取得相应的防渗效果。杨秀竹等[2]对悬挂式防渗帷幕的防渗效果作了详细的分析,认为当悬挂式防渗帷幕达到一定的深度和厚度要求时,除帷幕底部小范围内存在较大的渗流速度外,其它部分的渗流速度以及下游出溢处的水力梯度均有显著降低。谢兴华等[3]认为,从局部渗透稳定的角度出发,有限深度承压透水层中防渗墙的深度并非越深越好,而是存在最优深度。防渗墙太深,反而导致防渗墙端部渗透坡降增大。若覆盖层的颗粒级配不良,易出现局部渗透破坏,发生管涌等现象。王汉辉[4]认为防渗帷幕平面布置应结合隔水层或相对隔水层的分布及帷幕线路上的水文地质条件进行比选,以确定安全、经济、可靠的防渗线路。防渗帷幕剖面布置应综合考虑工程设计标准及水文地质条件等因素,确定剖面布置型式及帷幕深度。张景秀[5]认为防渗帷幕、防渗墙等堵漏设施并不是越严密、越坚实、越不透水越好,不仅加大工程量而且过多消费财力与时间。
研究者们[6-10]从不同角度对防渗帷幕的设计进行论证,均体现出一个学术思想,即大坝防渗结构的深度、长度和厚度并非越大越好,而是应该有一个合理的度。那么,防渗帷幕的深度、长度和厚度之间有没有一个合理的内在联系呢?本文运用平衡防渗原理,对防渗帷幕采用“深度→长度→厚度”依次确定的优化设计方法,既可以保证大坝的防渗效果达到渗控要求,又可以实现经济最优。
本文首先介绍了防渗帷幕“平衡防渗法”的优化设计原理,通过西藏某水电站工程首部枢纽拦河坝工程实例详述了平衡防渗优化设计过程,通过三维有限元渗流分析结果验证了这一理论的合理性。论文的理论部分以大坝的防渗帷幕结构优化设计为例论述,其优化原理对防渗墙等同类水工结构设计同样适用。
1 防渗帷幕“平衡防渗”优化设计方法
所谓防渗帷幕结构优化设计的“深度→长度→厚度”依次设计的“平衡防渗法”,是指依据对渗控效果贡献性的大小和重要性顺序,将防渗帷幕的设计分为三大步,优先确定防渗帷幕的深度,再确定帷幕的长度,最后确定帷幕的厚度。其中,帷幕深度依据渗漏量和允许水力坡降的控制标准确定;左右岸的帷幕长度依据绕过两岸帷幕的渗流速度等于绕过坝基河床下帷幕的渗流速度确定;各部位帷幕的厚度依据穿过帷幕的渗流速度等于绕过坝基河床下帷幕的渗流速度确定。整个设计原则是在满足渗透稳定的前提下,保证工程区各部位的渗流得到平衡控制,既不能形成主渗流通道,也不能在某个部位防渗过当,达到全局最优的方法,将以上方法定义为“平衡防渗法”。
1.1坝基中防渗帷幕深度的确定
“平衡防渗法”的第一步是确定防渗帷幕的深度,当隔水层(或相对隔水层)在坝基河床下埋深较浅时,应选择封闭式帷幕,帷幕应深入隔水层顶板下5 m~10 m,局部地质缺陷部位应适当加深。不同规范规定不同坝高相应隔水层q值控制标准见表1。

表1 国内主要水工建筑物规范规定的防渗线控制标准
当无隔水层或隔水层(或相对隔水层)埋深较大时,帷幕深度难以达到隔水层,可根据工程需要,选择采用悬挂式防渗帷幕。
影响帷幕防渗效果的因素首先是深度,随着帷幕的加深,绕渗流量逐步减小,当帷幕深度超过一定界限值时,再继续加大帷幕的深度,将不再引起下游水头值的降低。这时帷幕的深度就是其有效深度。
实际设计时,可先按规范规定的防渗线控制标准确定出坝基及两岸帷幕的初始设防范围,然后计算渗透流量和水力坡降,在满足渗透流量控制标准和水力坡降控制标准的前提下确定出河床帷幕的最终设计深度。
1.2左右岸防渗帷幕长度的确定
第二步是确定左右岸防渗帷幕长度,确定方法如下:在满足坝体渗透稳定(i<[icr])和渗流量控制标准的前提下,控制两岸的最大绕渗速度vb等于防渗帷幕上下游地层中的最大绕渗速度vr。防渗帷幕的长度Lb可按式(1)计算:
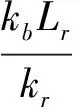
(1)
式中:Lr为防渗帷幕的深度,kb和kr分别为两岸岩体和坝基覆盖层(基岩)的渗透系数。若河床为多层覆盖层地基、左右岸为多层水平岩层时,kb和kr可按层状地层的综合渗透系数考虑。
1.3防渗帷幕厚度的确定
第三步确定防渗帷幕的厚度。与上述确定防渗帷幕长度的原理类似,在满足坝体渗透稳定(i<[icr])和渗流量控制标准的前提下,穿过防渗帷幕的最大渗流速度vc等于防渗帷幕上下游地层中的最大绕渗速度vr。防渗帷幕的厚度d可按式(2)计算:
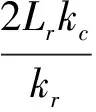
(2)
式中:Lr为防渗帷幕的深度,kc和kr分别为防渗帷幕和坝基覆盖层(基岩)的渗透系数。若河床为多层覆盖层地基kr可按综合渗透系数考虑。
防渗帷幕的深度超过以上计算值时,渗透水流优先选择从左右岸绕渗到达下游,超出计算值的帷幕深度无效;帷幕的长度和厚度超过以上计算值,渗透水流优先选择从河床帷幕下方绕渗到达下游,超出计算值的帷幕长度和厚度无效。帷幕的厚度小于此值,渗透水流优先选择穿越帷幕到达下游;帷幕的深度、长度小于以上计算值,则渗透水流将从帷幕下方、左右岸绕渗到下游。说明按以上方法确定的左右岸防渗帷幕的长度和厚度,既满足了防渗控制标准要求,又达到了最大程度节约投资的目的,是一种最优设计方法。
1.4帷幕施工质量控制标准研究
帷幕的施工质量较差时,其渗透性会增大。帷幕的施工质量如何控制,能否给出一个恰当的定量化标准呢,答案是肯定的。由式(2)得:

(3)
该式实际上是一个控制帷幕施工质量的量化标准。如2排帷幕的厚度近似取为2 m,当帷幕的深度为50 m时,该式变为kc=0.02kr。上式说明本工况帷幕的渗透系数至少应比河床覆盖层的渗透系数小50倍。否则,渗流由以通过帷幕底部的绕渗为主转化为以穿过帷幕的渗流为主,说明帷幕已经失去其应有的功效。显然,当帷幕的深度为75 m时,本工况帷幕的渗透系数至少应比河床覆盖层的渗透系数小75倍,否则帷幕失效。
式(3)同样适应于控制左右两岸的帷幕施工质量的量化标准的公式:
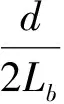
(4)
同理,若1排帷幕厚度为1 m,当帷幕长度为20 m时,帷幕的渗透系数至少应比河床覆盖层的渗透系数小40倍;当帷幕的长度为50 m时,帷幕的渗透系数至少应比河床覆盖层的渗透系数小100倍,否则帷幕失效。
2 西藏某水电站防渗帷幕优化设计
2.1工程概况
西藏某水电站为引水式电站,工程主要任务是发电,兼顾生态放水。水库正常蓄水位为3 425.00 m,死水位为3 422.00 m,水库总库容32.76×104m3,调节库容11.63×104m3;首部枢纽建筑物最大坝高28 m,电站总装机容量48 MW(3×16 MW),年发电量2.84×108kW·h,保证出力4.4 MW,年利用小时5 916 h。根据《水电枢纽工程等级划分及设计安全标准》[16](DL5180-2003)的规定,结合本工程装机容量,确定本工程为四等小(1)型工程。
挡水建筑物采用土工膜防渗堆石坝,与上游围堰结合,最大坝高28 m。上游坝坡在3 419.0 m以上坡比为1∶2.8,3 419.0 m~3 411.0 m之间坡比为1∶1.8,高程3 412.0 m以下坡度为1∶2.5。下游坝面3 411.0 m高程以上坡比为1∶1.8,在3 411.0 m高程设一条宽2 m的马道,3 411.0 m高程以下坡比为1∶2。坝体下游采用贴坡排水。土工膜防渗结构从上游至下游依次为预制混凝土、砾石保护层、复合土工膜、砾石垫层。坝内设置有L型排水体,下游坝脚部位设置有贴坡排水,L型排水体与下游贴坡排水相接,竖向排水体和贴坡排水上游设反滤保护层,水平排水体底部基础表面也设有反滤保护层,以防止坝体和坝基砂砾料中细颗粒流失。拟定的坝体基本断面见图1。工程区主要材料渗透系数如表2所示。
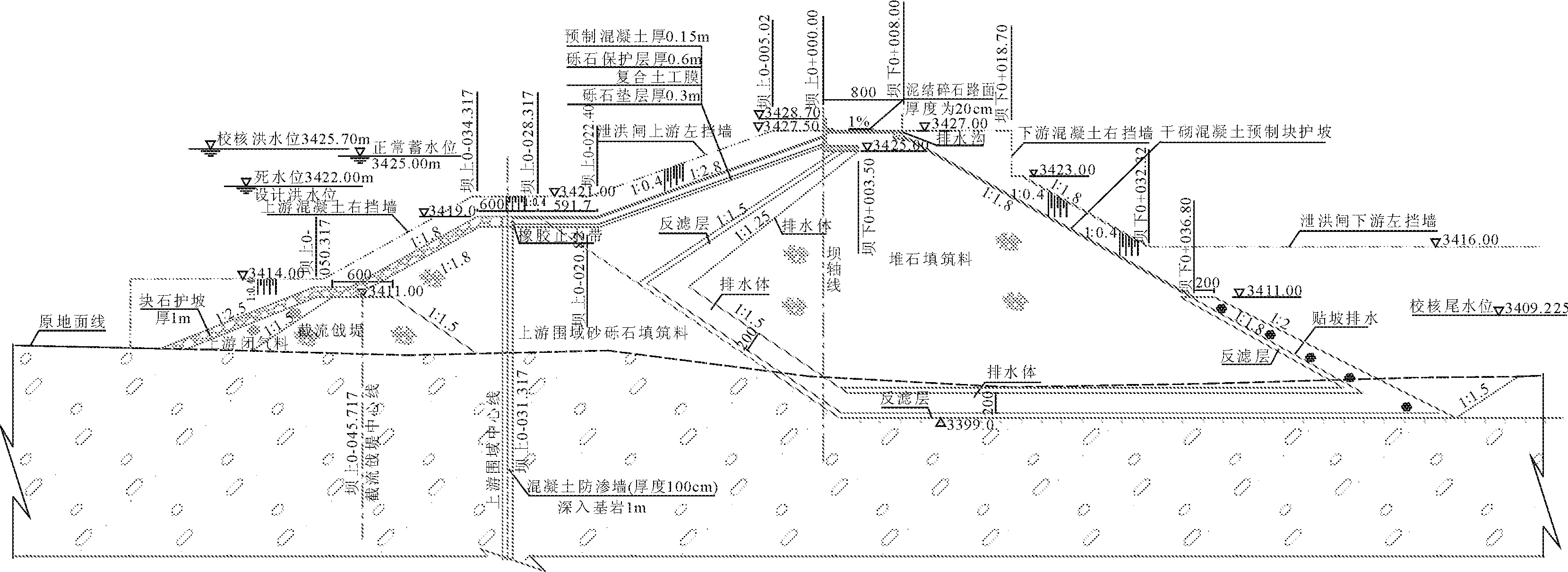
图1左岸复合土工膜堆石坝标准剖面图

表2 坝址区主要材料渗透系数
2.2防渗墙深度和厚度研究
该水电站工程首部枢纽基础坐落在覆盖层之上,覆盖层厚度50 m~80 m。河床部分防渗体设计为:左岸土工膜防渗堆石坝基础采用1 m厚的混凝土防渗墙,深入基岩1 m,坝体采用土工膜防渗。泄洪冲砂闸、排漂闸、取水口等混凝土建筑基础防渗采用1 m厚的混凝土防渗墙,深入基岩1 m。根据防渗要求,需研究采用悬挂式混凝土防渗墙的可能性。
假设悬挂式混凝土防渗墙的深度分别取坝高1倍、坝高1.5倍和坝高2倍。由于大坝的设计坝高为28 m,因此,渗透水流由防渗墙上游河床绕过防渗墙底部到达下游河床的渗透路径长度分别为56 m、84 m和112 m。正常蓄水位时上下游最大水头差为20.14 m。因此,以上3个防渗墙深度对应的河床覆盖层的平均水力坡降分别为0.360、0.240和0.180,水力坡降均较大。
坝基砂砾石覆盖层的渗透系数为5.51×10-5m/s,按以上水力坡降计算,坝前砂砾石覆盖层中的最大渗流速度分别为1.98×10-5m/s、1.32×10-5m/s和0.99×10-5m/s;坝前单位平方米面积的砂砾石覆盖层中的渗流量分别为0.0198 L/s、0.0132 L/s和0.0099 L/s。若考虑坝前砂砾石覆盖层的总面积,总体渗流量均较大。
悬挂式混凝土防渗墙只能起到延长渗透路径的目的,达不到截渗的效果,因此,即便防渗墙的深度较大,坝基的渗流速度和渗流量仍然较大。坝基砂砾石覆盖层建议采用原设计防渗方案,即封闭式混凝土防渗墙。
深入基岩1 m,基岩渗透系数为5×10-7m/s,防渗墙底部绕渗速度:
vr=5.0×10-7×20.14/(1×2)=5.035×10-6m/s
防渗墙的渗透系数1.0×10-8m/s远小于覆盖层5.51×10-5m/s和弱风化基岩5.0×10-6m/s的渗透系数,1 m厚的防渗墙相当于5 510 m厚度的覆盖层的阻渗效果、相当于500 m厚度的弱风化基岩的防渗效果,因此,从渗控要求来说防渗墙的厚度可以设计很薄,其厚度应根据受力要求确定。
2.3防渗帷幕水平长度和厚度研究
本工程左右两岸基岩防渗采用水泥帷幕灌浆,在左、右岸坝肩各设一层帷幕灌浆硐,高程为3 427.00 m,均向岸里延伸50 m。帷幕灌浆硐断面为城门洞型,衬砌后断面为3.0 m×3.5 m。水泥灌浆帷幕采用单排孔,孔距2 m,平均孔深45 m。岩体相对隔水层透水率按5 Lu控制。根据防渗要求,需研究左右两岸防渗帷幕灌浆区的长度范围。
假设左右两岸防渗帷幕灌浆区的水平长度分别为25 m、50 m、75 m和100 m,渗透水流水平绕过防渗帷幕左右端的绕渗路径长度为以上水平长度的2倍,分别为50 m、100 m、150 m和200 m。左右两岸坝肩弱风化层的渗透系数为5.0×10-6m/s,微风化基岩的渗透系数为1.0×10-6m/s,以上4种工况时两种材料所占的面积比例按1∶1、1∶3、1∶5和1∶7考虑,坝基横剖面图如图2所示,帷幕灌浆区的以上4种水平长度对应的左右岸加权平均渗透系数分别为1.67×10-6m/s,1.25×10-6m/s,1.15×10-6m/s和1.11×10-6m/s。
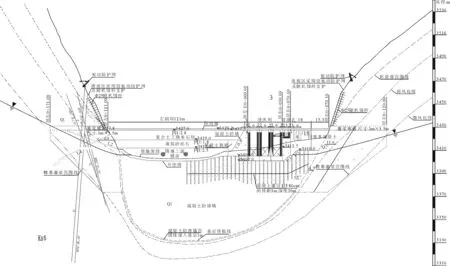
图2坝基横剖面图
因此,上下游水头差为H深度处,以上4个帷幕灌浆水平长度对应的两岸平均水力坡降分别为0.02H、0.01H、0.0067H和0.005H;若帷幕上下游的最大水头差按20.14 m考虑,则两岸平均水力坡降分别为0.403、0.202、0.135和0.101。可见,对于考察两岸基岩渗透稳定性来说,水力坡降均较小。
帷幕上下游最大水头差为H时,以上4个帷幕灌浆水平长度对应的两岸平均渗流速度分别为3.34×10-8Hm/s,1.25×10-8Hm/s,7.705×10-9Hm/s和5.55×10-9Hm/s;若帷幕上下游最大水头差按20.14 m考虑,则两岸平均渗流速度分别为6.73×10-7m/s,2.52×10-7m/s,1.55×10-7m/s和1.12×10-7m/s。
对灌浆帷幕的厚度也进行研究:
灌浆帷幕设计采用单排孔,孔距2 m,帷幕厚度也为2 m。同时,对比研究帷幕采用双排孔,厚度为4 m工况。灌浆帷幕的渗透系数为2×10-7m/s。则帷幕上下游最大水头差为H时,穿过单排帷幕和双排帷幕的渗流速度分别为1.0×10-7Hm/s和5.0×10-8Hm/s;若帷幕上下游最大水头差按20.14 m考虑,则穿过单排帷幕和双排帷幕的渗流速度分别为2.01×10-6m/s和1.01×10-6m/s。
由以上计算结果可见,若采用单排孔灌浆帷幕,穿过帷幕的渗流速度为2.01×10-6m/s,若双排孔灌浆帷幕,此时穿过帷幕的渗流速度为1.01×10-6m/s;绕过水平长度为50 m的防渗帷幕的渗流速度为2.52×10-7m/s,说明水平长度为50 m的防渗帷幕已经足够长,超过此长度的帷幕是发挥不到防渗效应的。建议采用双排孔灌浆帷幕,水平防渗长度50 m即能满足防渗要求。
2.4防渗帷幕垂直向深度研究
左右两岸坝肩弱风化层的渗透系数为5.0×10-6m/s,微风化基岩的渗透系数为1.0×10-6m/s。帷幕底部渗透水流可以直接通过河床砂砾石覆盖层进入弱风化基岩和微风化基岩绕渗,最长渗透路径可按5 m×2考虑,最大水头差按20.14 m计算,则帷幕底部绕过弱风化基岩和微风化基岩的渗流速度分别为:
vr1=5.0×10-6×20.14/(5×2)=1.007×10-5m/s
vr2=1.0×10-6×20.14/(5×2)=2.014×10-6m/s
可见,帷幕底部的绕渗速度大于水平绕渗速度,且大于穿过帷幕的渗流速度,说明需要加强这一区域的渗控措施。
2.5防渗帷幕施工质量控制
若防渗帷幕施工质量较差,灌浆帷幕的渗透系数为2×10-6m/s。则帷幕上下游最大水头差为H时,穿过单排帷幕和双排帷幕的渗流速度分别为1×10-6Hm/s和0.5×10-6Hm/s;若帷幕上下游最大水头差按20.14 m考虑,则穿过单排帷幕和双排帷幕的渗流速度分别为2.014×10-5m/s和1.007×10-5m/s。
2.6防渗结构优化设计结果分析
将以上解析法估算的各种工况时大坝关键部位的最大渗流速度汇总于表3,根据文中提出的防渗结构优化设计的“平衡防渗法”,原设计防渗体的薄弱防渗部位一目了然。由表3可见,采用任何深度的悬挂式防渗墙时防渗墙底部的绕渗速度都较大,说明必须采用封闭式防渗墙,封闭式防渗墙应该深入基岩。深入基岩1 m,防渗墙底部绕渗速度为5.035×10-6m/s。混凝土防渗墙厚度在满足应力要求作用下可取为1 m,穿过防渗墙的渗流速度为2.01×10-7m/s。两岸帷幕水平长度可以取50 m,两岸平均渗流速度2.52×10-7m/s。帷幕底部的弱风化基岩区是一个防渗薄弱区,帷幕底部的绕渗速度为1.007×10-5m/s,应该加强这一区域的防渗结构设计;当帷幕施工质量较差,穿过帷幕的渗流速度也较大,应该保证帷幕的施工质量。
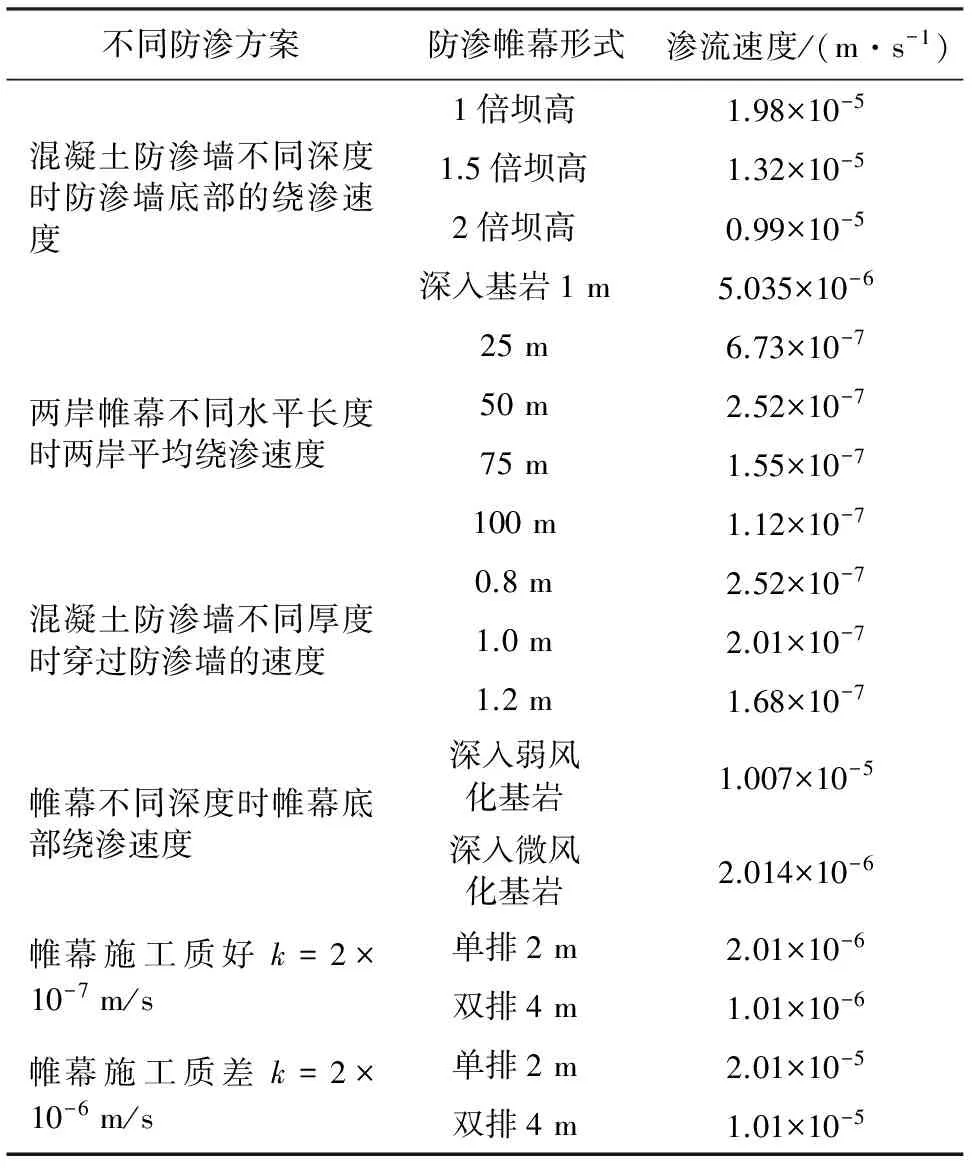
表3 解析估算的大坝关键部位的最大渗流速度
以上依据防渗帷幕结构优化设计的“平衡防渗法”,即在满足渗透稳定的前提下,要求工程区各部位的渗流得到平衡控制,既不能形成主渗流通道,也不能在某个部位防渗过当,达到全局最优的方法,对西藏某水电站工程首部枢纽防渗结构包括防渗墙深度和厚度、防渗帷幕的水平长度垂直深度和厚度进行了优化设计研究,对原设计防渗方案提出了以下优化设计建议:
(1)建议采用封闭式混凝土防渗墙,防渗墙的深度应该“深入基岩1 m”。
(2)建议弱风化岩区采用双排孔灌浆帷幕,帷幕深入两岸山体的水平长度建议为进入微风化岩体25 m(水平防渗深度为50 m),超过此长度的帷幕是发挥不到防渗效应的。
(3)建议增加弱风化层中的灌浆帷幕深度,即帷幕在垂直方向穿透弱风化层。
(4)帷幕是防渗结构的薄弱环节,穿过帷幕的渗流速度相对也较大,因此,应保证帷幕的施工质量。
3 三维有限元渗流计算验证
研究非稳定渗流问题需要求解非稳定渗流场,也就是要对方程(5)[17-18]进行有限元求解。
(5)
式中:kx,ky,kz分别为x,y,z方向上的渗透系数;Ω为渗流区域;Γ1为水头边界;Γ2为流量边界;q为边界法向流量;H0为初始时刻的水头值;H1为边界水头;μs为贮水率。本文研究内容属于三维各向同性稳定渗流问题,只需令方程(5)中的贮水率为0,且各向渗透系数相等。
利用Seep-3d有限元分析软件,建立三维有限元模型如图3,计算边界施加如图4,河道内全部为指定水头边界条件,其中上游水头为正常蓄水位3 425.00 m,下游水头高度为3 404.86 m;模型底部为不透水边界;根据河床的排渗条件决定计算模型两侧的渗透边界条件,依据工程地质报告,两岸山体受大气降水向河内排泄,计算中模型的左右两侧设为不透水边界。有限元网格划分如图5,计算中采用八面体等参数单元网格,整个模型共划分出节点数198 352个,单元数为210 625个。对防渗帷幕取不同深度、长度以及厚度进行计算,计算工况如下。
工况1:设计防渗方案,混凝土防渗墙深度按入岩1 m、左右岸防渗帷幕向岸里延伸50 m。坝体防渗土工膜均按实际设计尺寸,大坝蓄水至正常蓄水位3 425.00 m,坝后水位为3 404.86 m。
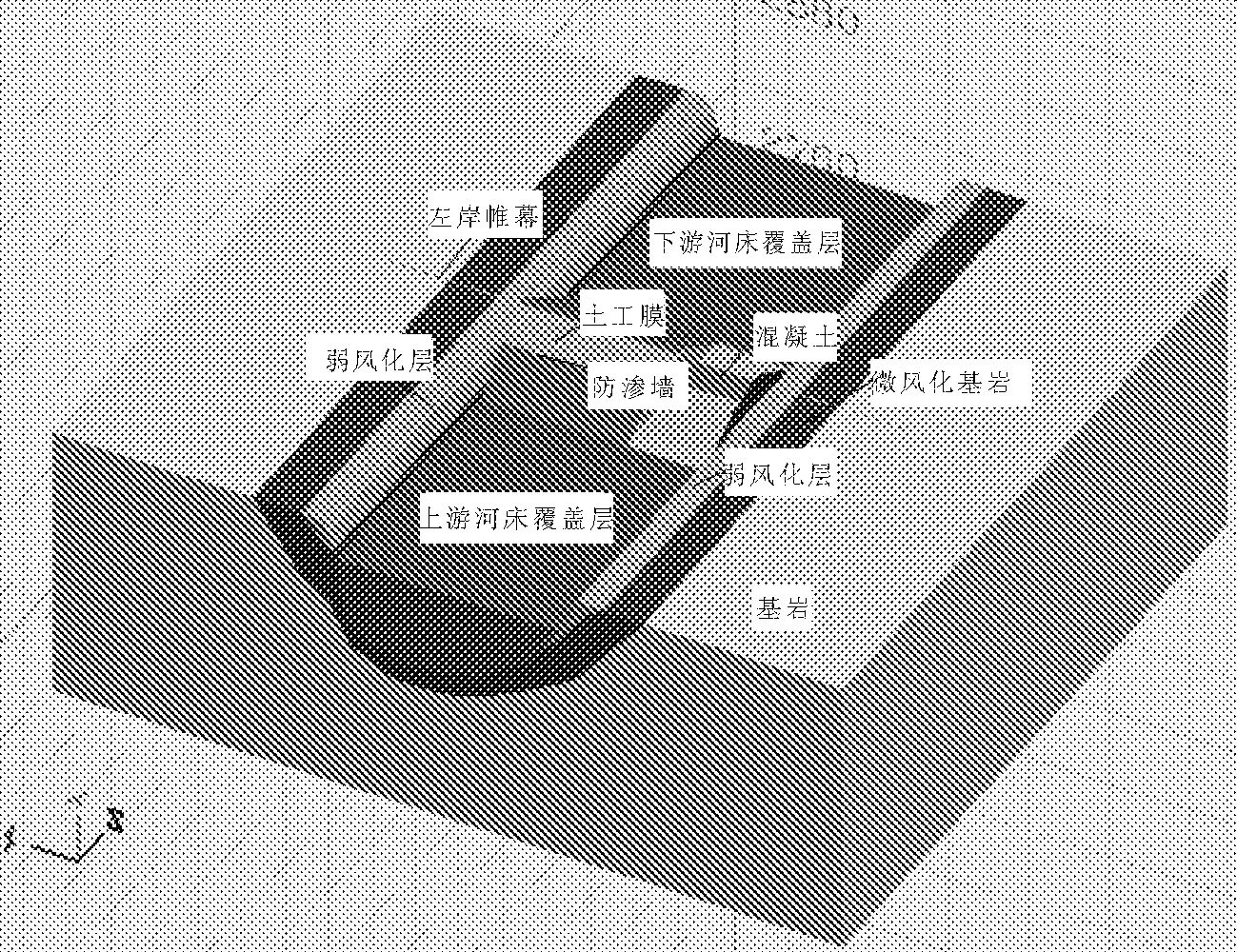
图3大坝渗流计算模型及材料分区
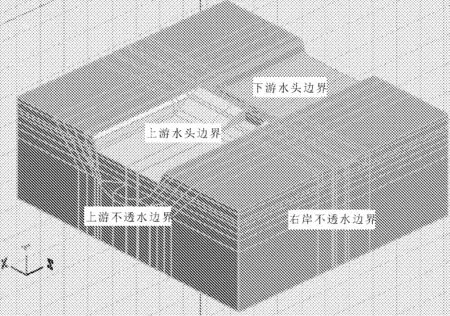
图4计算边界施加示意图

图5三维渗流计算网格划分图
工况2~工况4:悬挂式混凝土防渗墙深度分别取1倍坝高、1.5倍坝高、2倍坝高,其它计算参数同工况1的渗流计算。
工况5~工况7:混凝土防渗墙深度按入岩1 m,左右岸防渗帷幕分别向岸里延伸25 m、75 m、100 m,其它计算参数同工况1的渗流计算。
各工况计算结果见表4、表5。工况1计算的一个水平剖面和顺河剖面处的水头和水力坡降分布如图6~图9所示,由图可以看出,水头等值线分布均匀,符合常规规律,各部位的水力坡降较小,均可满足设计要求。说明采取优化设计方案在渗流量控制和渗透坡降控制方面均能够满足渗透稳定的要求。
工况2~工况4由于采取悬挂式混凝土防渗墙,计算的总体渗流量均较大,原因是悬挂式混凝土防渗墙只能延长渗透路径,没有达到截渗的目的,而且堆石坝下游坡脚处的水力坡降也较大,不利于坝坡稳定。
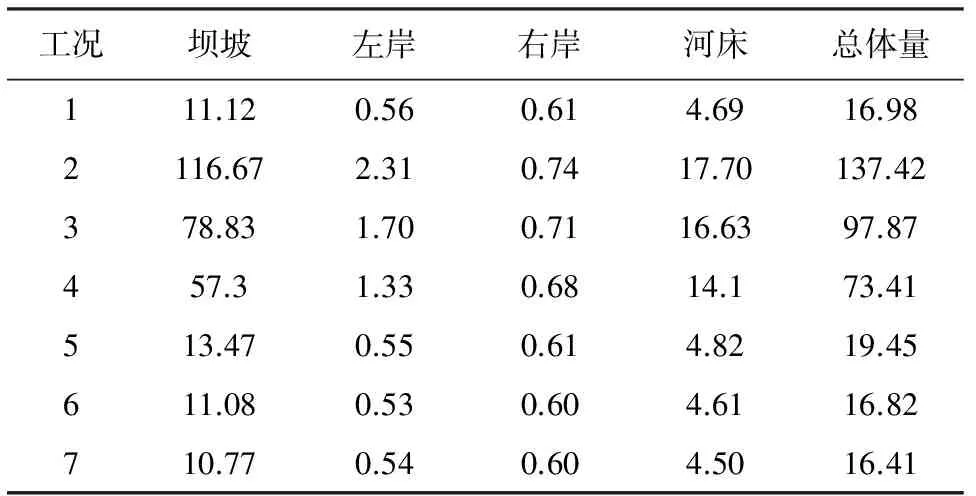
表4 各种工况的渗透流量 单位:L/s
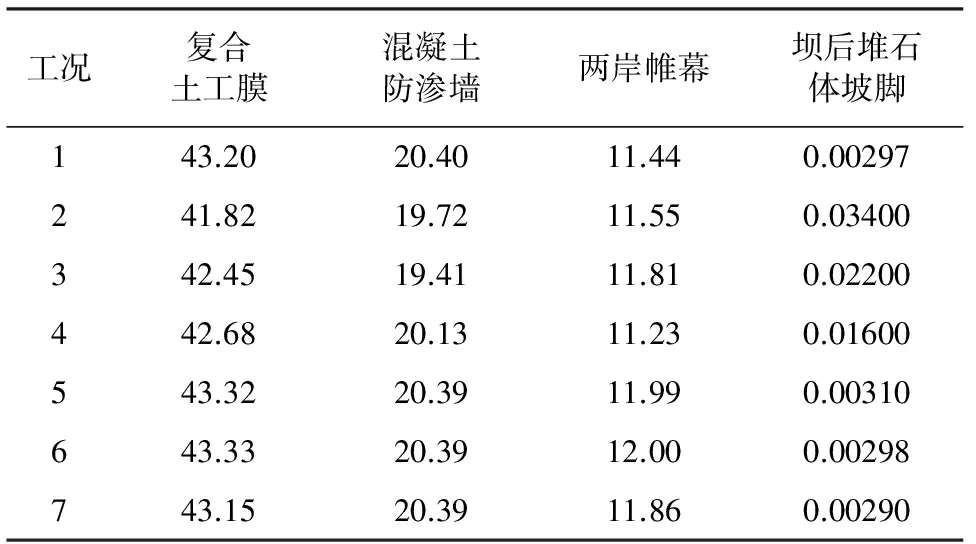
表5 坝体内各关键部位的最大水力坡降
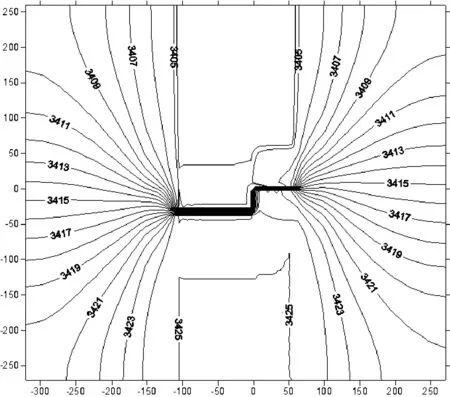
图6高程3398m水头等值线图
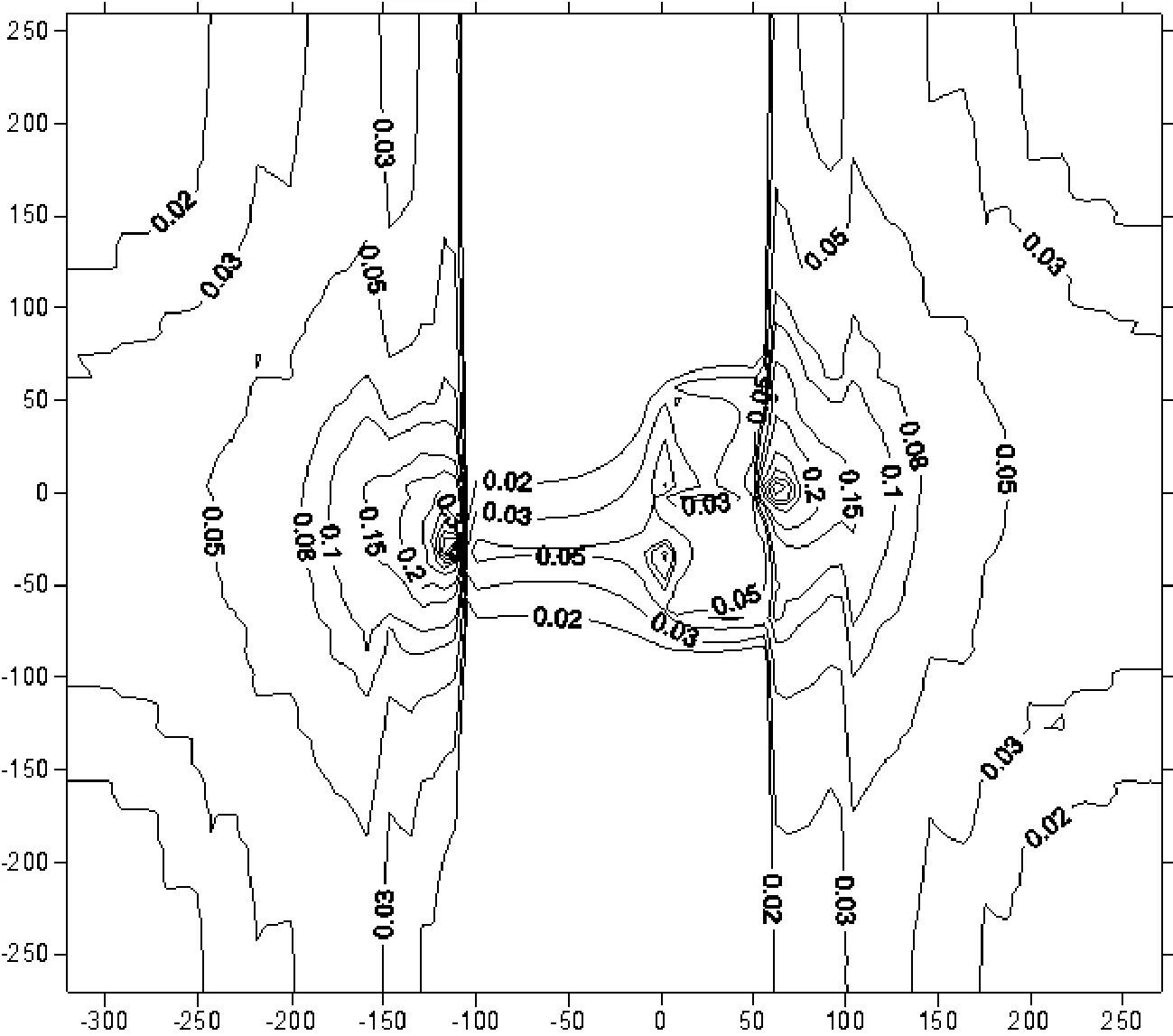
图7高程3398m处水力坡降等值线图
工况5计算的渗流量较优化设计方案有所增大,堆石坝下游坡脚处的水力坡降较小,能满足渗透稳定要求。工况6、工况7计算的渗流量较优化设计方案有所减小,但减小幅度不大,堆石坝下游坡脚处的水力坡降较小,能满足渗透稳定要求。因此,左右岸防渗帷幕入岩深度确定为50 m比较合适,即优化设计方案。
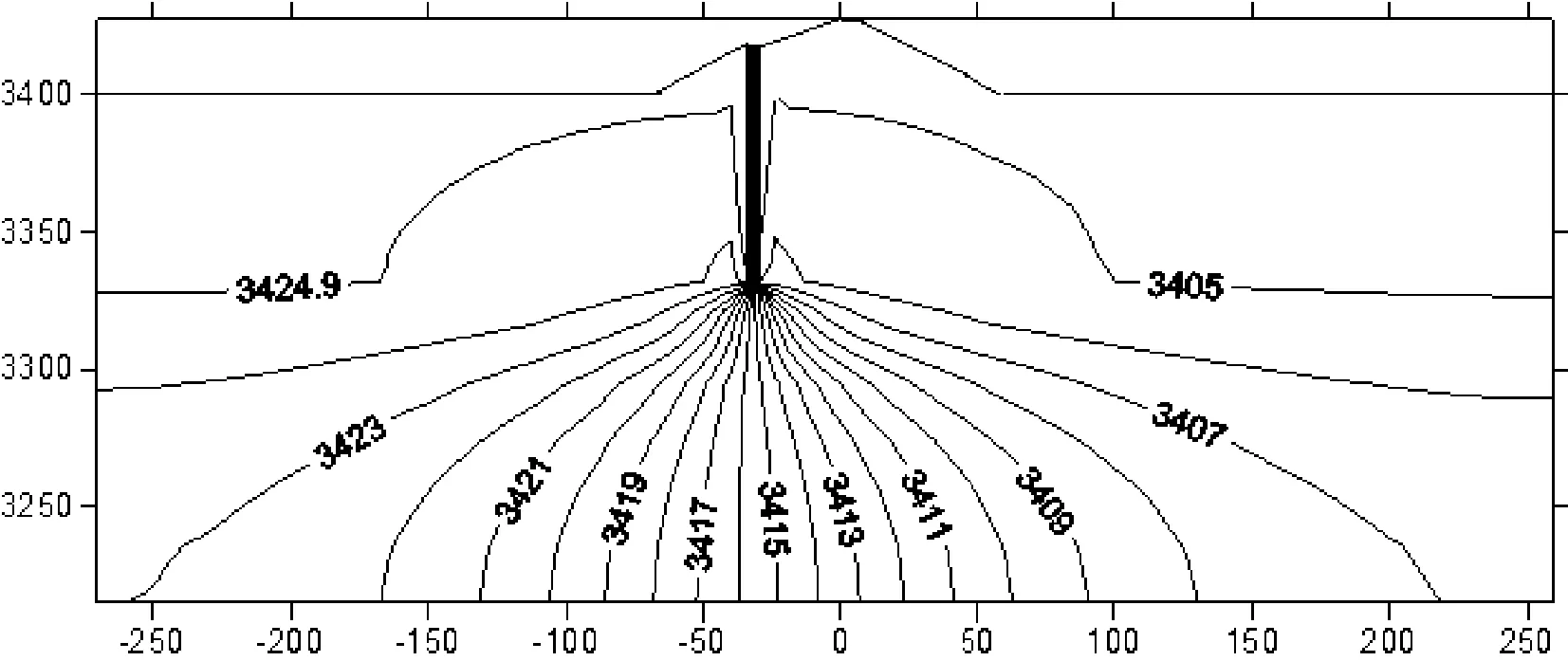
图8顺河剖面的水头等值线图
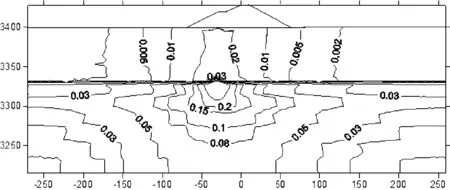
图9顺河剖面的水力坡降等值线图
4 结 语
本文运用“平衡防渗法”,即依据渗漏量和允许水力坡降的控制标准确定防渗帷幕深度,再依据绕过两岸帷幕的渗流速度等于绕过坝基河床下帷幕的渗流速度确定防渗帷幕长度,依据穿过帷幕的渗流速度等于绕过坝基河床下帷幕的渗流速度确定防渗帷幕的厚度,对西藏某水电站工程首部枢纽拦河坝不同防渗方案进行了优化设计,认识到防渗帷幕的设计应该保证工程区各部位的渗流得到平衡控制,既不能形成主渗流通道,也不能在某个部位防渗过当,达到全局最优的方法。最后,通过三维有限元软件的计算结果分析,验证了 “平衡防渗法”结构设计的合理性。
参考文献:
[1]杜延龄,许国安.岩基灌浆帷幕合理渗透性和深度的初步研究[J].水利水电技术,1980,(6):52-56.
[2]杨秀竹,陈福全,雷金山,等.悬挂式帷幕防渗作用的有限元模拟[J].岩土力学,2005,26(1):105-107.
[3]谢兴华,王国庆.深厚覆盖层坝基防渗墙深度研究[J].岩土力学,2009,30(9):2708-2712.
[4]王汉辉,邹德兵,夏传星,等.水利水电工程中防渗帷幕布置原则与方法[J].水利与建筑工程学报,2010,8(6):117-120.
[5]张景秀.对坝基防渗标准与实施方法若干问题的探讨[C]//中国水电基础局有限公司.第八次水利水电地基与基础工程学术会议论文集,2006:118-123.
[6]尹海华.无限深土石坝坝基悬挂式垂直防渗体防渗方法初探[J].甘肃水利水电技术,2012,48(7):33-35.
[7]毛海涛,侍克斌,马铁城.新疆透水地基上土石坝防渗墙有效深度研究[J].人民长江,2008,39(19):81-84.
[8]王晓燕,党发宁,田威,等.大渡河某水电站围堰工程中悬挂式防渗墙深度的确定[J].岩土工程学报,2008,30(10):1564-1568.
[9]张宜虎,尹红梅,杨裕云,等.燕山水库坝基防渗墙优化设计[J].岩土力学,2005,26(7):1161-1164.
[10]王学武,党发宁,蒋力,等.深厚复杂覆盖层上高土石围堰三维渗透稳定性分析[J].水利学报,2010,41(9):1074-1078.
[11]中华人民共和国水利部.SL274-2001.碾压式土石坝设计规范[S].北京:中国水利水电出版社,2001.
[12]中华人民共和国水利部.SL282-2003.混凝土拱坝设计规范[S].北京:中国水利水电出版社,2003.
[13]中华人民共和国水利部.SL319-2005.混凝土重力坝设计规范[S].北京:中国水利水电出版社,2005.
[14]中华人民共和国水利部.SL253-2000.溢洪道设计规范[S].北京:中国水利水电出版社,2000.
[15]中华人民共和国水利部.SL266-2001.水电站厂房设计规范[S].北京:中国水利水电出版社,2001.
[16]中华人民共和国国家经济贸易委员会.DL5180-2003.水电枢纽工程等级划分及设计安全标准[S].北京:中国电力出版社,2003.
[17]毛昶熙.渗流计算分析与控制[M].北京:水利电力出版社,2003.
[18]谢定义,姚仰平,党发宁.高等土力学[M].北京:高等教育出版社,2008.
StudyonOptimizedDesignofAHydropowerStationinTibetBasedonEquilibriumSeepagePrevention
DANG Fa-ning1,XIONG Lu1,WANG Zhen-hua1,2,TIAN Hong-mei1
(1.InstituteofGeotechnicalEngineering,Xi'anUniversityofTechnology,Xi'an,Shaanxi710048,China;2.NorthwestElectricPowerDesignInstituteofChinaPowerEngineeringConsultingGroup,Xi'an,Shaanxi710075,China)
Abstract:The impervious curtain in different seepage zone is designed based on the idea of equilibrium seepage prevention,which is,the depth of the impervious curtain is determined firstly by the critical values of the leakage and the permitted hydraulic slope.And then,on the condition that the velocity of the seepage flow around the two sides of the banks and dam foundation is equivalent,the extension length of the impervious curtain can be determined.Finally,the thickness of the impervious curtain can be determined by assuming the velocity of the seepage flow though the impervious curtain is equivalent to that of around the dam foundation.As a result,excessive or insufficient anti-seepage design of the impervious curtain can be avoided,so as to reach the global optimum.A Hydropower Station in Tibet was taken as an example of optimizing the design of different impervious programs in different seepage zones.According to the result of a three-dimensional finite element analysis,the reliability of the structure design based on equilibrium seepage prevention was verified.The results of this study provides reference not only to the impervious program modification of the existing dam,but also to the design of impervious curtains of similar embankment dams.
Keywords:impervious curtain;seepage flow velocity;optimized design
DOI:10.3969/j.issn.1672-1144.2014.06.001
中图分类号:TV223.6
文献标识码:A
文章编号:1672—1144(2014)06—0001—08
作者简介:党发宁(1962—),男,陕西富平人,教授,主要从事岩土计算力学方面的教学与科研工作。
基金项目:陕西省黄土力学与工程重点实验室重点科研计划项目(09JS103);水利部公益性行业科研专项(201201053-03)
收稿日期:2014-05-09修稿日期:2014-06-27
