垃圾填埋场边坡动力响应时程分析

李　勇

(广东石油化工学院 建筑工程学院，广东 茂名 525000)



垃圾填埋场边坡动力响应时程分析

李勇

(广东石油化工学院 建筑工程学院，广东 茂名 525000)

摘要：随着城市化建设和新农村建设进程的提速，对环境的要求也更高。目前，设置垃圾填埋场仍是处置城市生活垃圾的一种行之有效且最常用的方法。填埋场边坡与其它自然边坡和人工边坡一样，也存在边坡稳定问题，针对锡塘垃圾填埋场边坡工程实际，基于时程分析法对填埋场边坡的动力响应进行了分析，采用等效线性化方法考虑垃圾填埋体的非线性动力响应特性。为充分反映地震动特性对填埋场动力响应的影响，地震动输入采用三条实测波和一条人工地震波。分析结果表明，不同地震波对填埋场地震响应有显著差异，在对实际填埋场抗震设计时，至少应选择两条实测波加一条人工合成地震波作为输入地震波，这样才能较好反映填埋场动力响应特性。

关键词：动力响应；时程分析；边坡；垃圾填埋场

填埋场边坡与其它自然边坡和人工边坡一样，也存在边坡稳定问题。从地震稳定性角度来看，填埋场边坡最显著的特点是具有较大规模，复杂的由多种不同性质材料组成的密封覆盖层和衬垫系统，填埋体通常具有明显的非均质性和各向异性，其性质还因组成物质的腐烂，分解而随时间变化[1-4]。时程分析法从选定的输入地震波(地震波加速度时程)出发，采用多节点多自由度的边坡有限元动力计算模型建立动力方程，采用逐步积分法对方程进行求解，计算地震过程中每一瞬时边坡的位移、速度和加速度响应，从而可以分析出边坡在地震作用下的内力变化及边坡失稳的全过程。时程分析可详细了解边坡在整个地震持时内的边坡响应。而且除了在进行时程积分时引入了一些假定外，时程分析法基本没有其它限制，适用范围较广，是边坡地震响应分析的有力工具。时程分析法的主要缺点是计算结果过度依赖于所选取的地震加速度时程曲线，离散性很大。通常要对许多条地震波曲线进行计算并加以综合处理，才能对边坡的抗震性能进行较为客观的评价[5-8]。本文采用更符合实际情况的动力时程法进行时程分析，选取EL-Centro波、宁河波、迁安波和人工地震波(超越概率10%)作为输入地震波，利用Plaxis软件中的HSsmall本构模型对某城市垃圾填埋场边坡进行动力时程分析，选取边坡在EL-Centro波作用下的计算结果进行分析，该结果可为填埋场的抗震设计及分析提供参考并对填埋场抗震设计具有指导意义。

1　填埋场动力响应分析方法

在垃圾填埋场地震时程分析中，将垃圾土体考虑为粘弹性体。动力有限元控制方程为[9-11]：

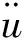
(1)

2　所采用的本构模型

计算时采用Plaxis软件中的HSsmall模型，HSsmall模型是弹塑性双曲线模型，与土的硬化模型相类似。当该模型用于动力分析时，包含了材料的粘滞阻尼。模型中采用Konder[12]、Hardin和Drnevich[13]所给出的双曲线来描述土的动应力应变关系骨干曲线。由于其形式简单，计算参数少，在实际工程计算中得到广泛应用。HSsmall模型的基本公式为：

Gs/G0=1/(1+|γ/γr|)

(2)

其中：Gs为割线剪切模量；γ为剪应力；G0为小应变时的剪切模量；γr为极限剪应变，γr=τmax/G0，τmax为破坏时的剪应力，即最大剪应力。

3　填埋场边坡动力分析模型建立

3.1填埋场边坡计算模型

以某实际填埋场为工程背景，建立如图1所示的有限元分析模型。特征点布置图如图2所示。垃圾土的力学参数如表1所示[14-15]。Plaxis软件提供了6节点单元和15节点单元两种，如图1所示，本文采用的是15节点单元，利用Plaxis软件自动划分网格单元，在“划分精度”中选择“细密”，整体网格见图1，模型单元数442，节点数4 005。

图1有限元计算模型

图2填埋场特征点设置

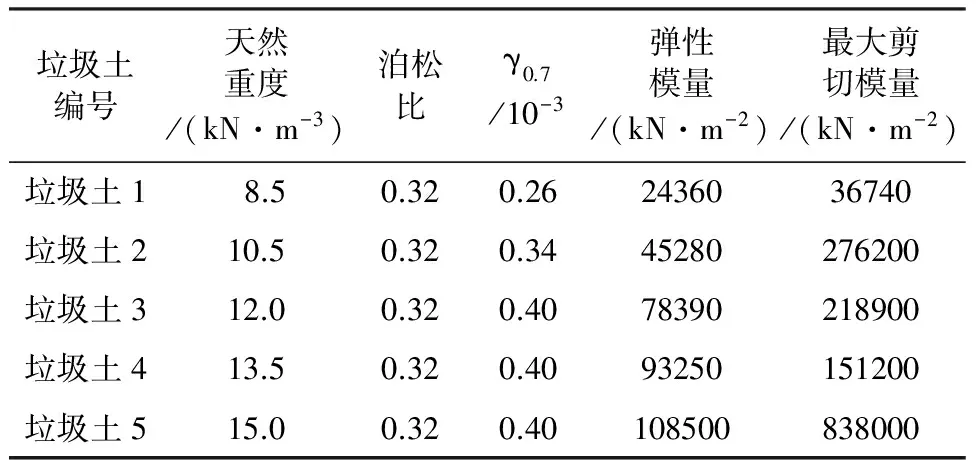
表1　垃圾填埋场基本计算参数

3.2地震动输入

为了研究边坡动力响应，选取了具有不同频谱特性和持时的三条实测波(EL-Centro波、迁安波、宁河波)和一条人工波。时程曲线见图3～图6。对于EL-Centro波，能量主要集中在频率为3 Hz～7 Hz范围内，对于迁安波，能量主要集中在频率为5 Hz～20 Hz范围内，对于宁河波，能量主要集中在频率为5 Hz范围以内，人工合成波总持时为30 s，时间间隔均为0.02 s，能量主要集中在频率为3 Hz～6 Hz范围内[16-17]。

4　填埋场边坡动力响应时程分析

4.1加速度响应

选择填埋场边坡坡顶(节点A)、坡中(节点B)、坡脚(节点C)及底部(节点E)进行边坡动力响应分析。由图7可以看出，从节点E到节点A，即从填埋场底部到坡顶，加速度峰值逐渐增大，到坡中处达最大值，体现了填埋层具有放大地震的作用；图8给出了坡顶加速度变化规律，从图8中可以看出，在动力响应过程中，坡顶峰值加速度为3.38 m/s2，约为输入峰值加速度的3.4倍。

图3EL-Centro地震波加速度时程曲线

图4迁安地震波加速度时程曲线

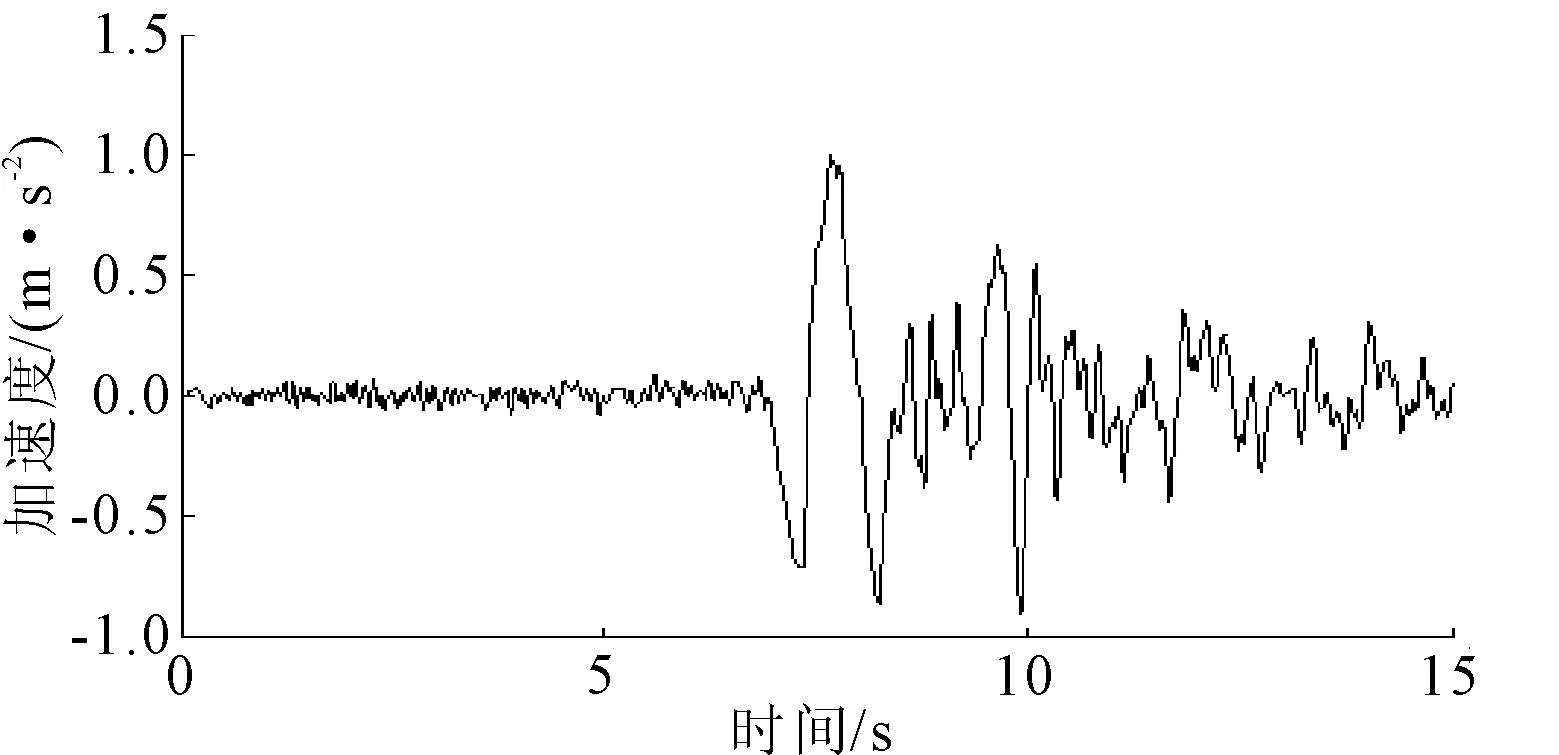
图5宁河地震波加速度时程曲线

图6人工合成地震波加速度时程曲线

4.2位移响应

由图9、图10可以看出，边坡坡顶的位移响应最大，达0.055 m，发生在25.64 s时，坡顶端的位移为坡体底部位移的1.08倍。从时间上看，在动荷载的开始初期，除边坡边缘节点位移略大于其它节点，边坡总体位移基本一致；继续施加地震动，边坡边缘质点的位移超过边坡底部与垃圾坝体的位移，这种现象随着地震继续更加明显。垃圾坝与边坡底部的位移时程曲线基本一致，因此边坡位移的水平方向的放大作用不明显，出现这种现象的原因是因为影响地表质点运动的瑞雷波在地震过程中衰减较快造成的。边坡位移与地震加速度变化有较强的关联性，但位移的变化相对地震加速度的变化有明显的滞后。这与文献[18]所得到的结果基本一致。

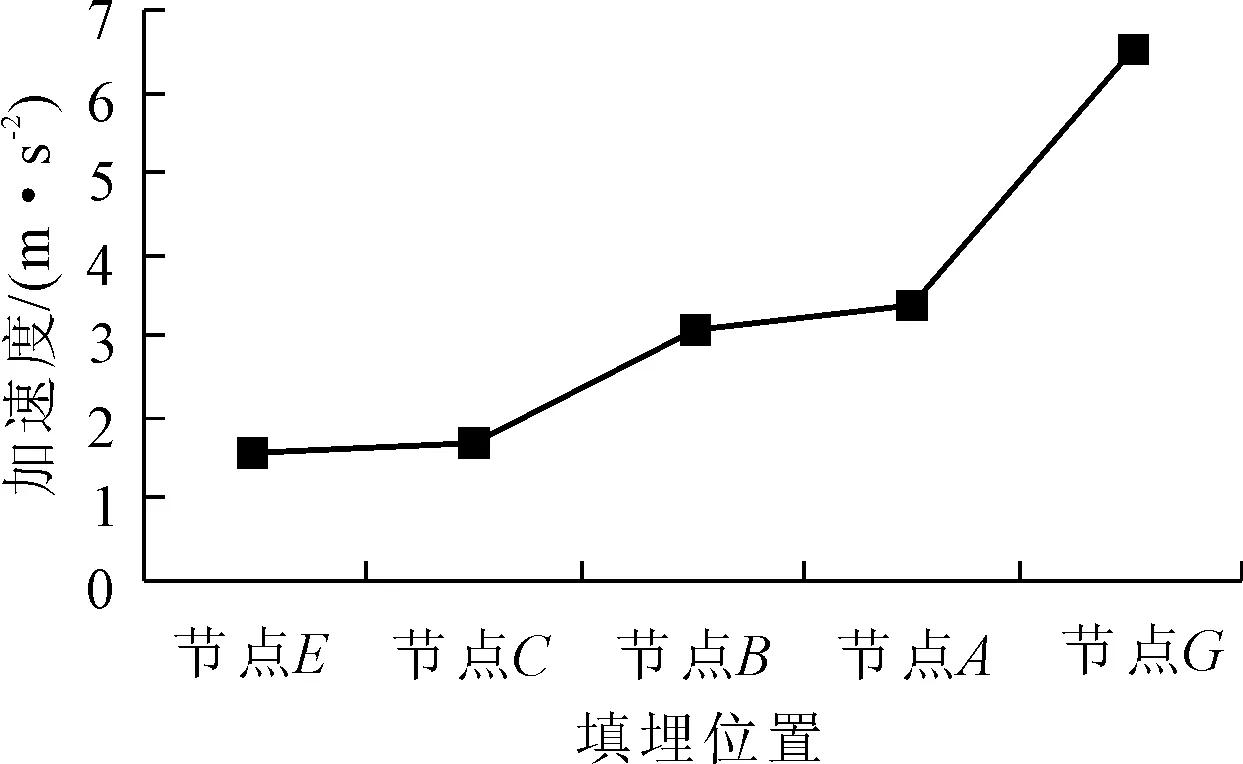
图7填埋高度与加速度关系

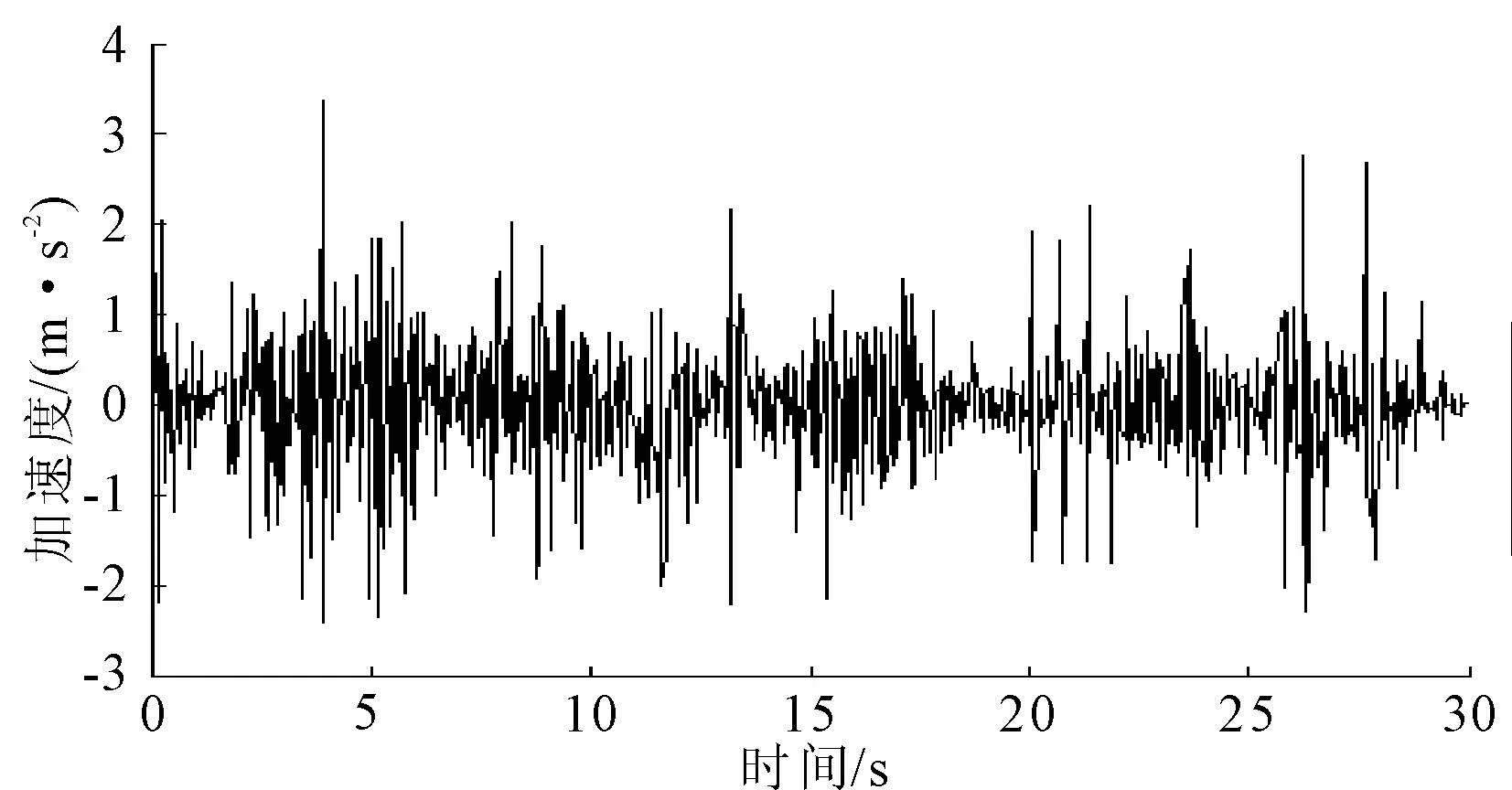
图8EL-Centro波作用下坡顶加速度响应时程曲线

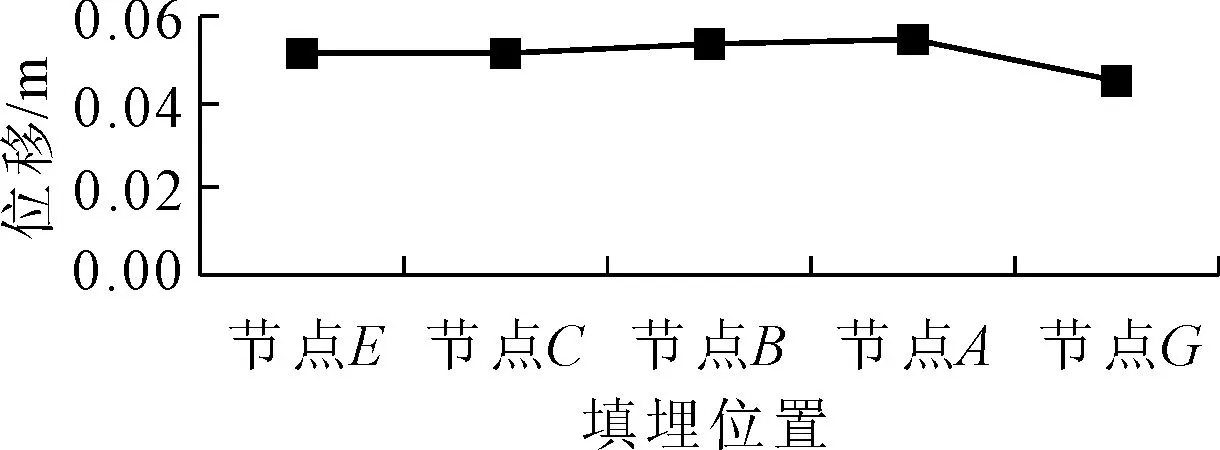
图9填埋高度与位移关系图

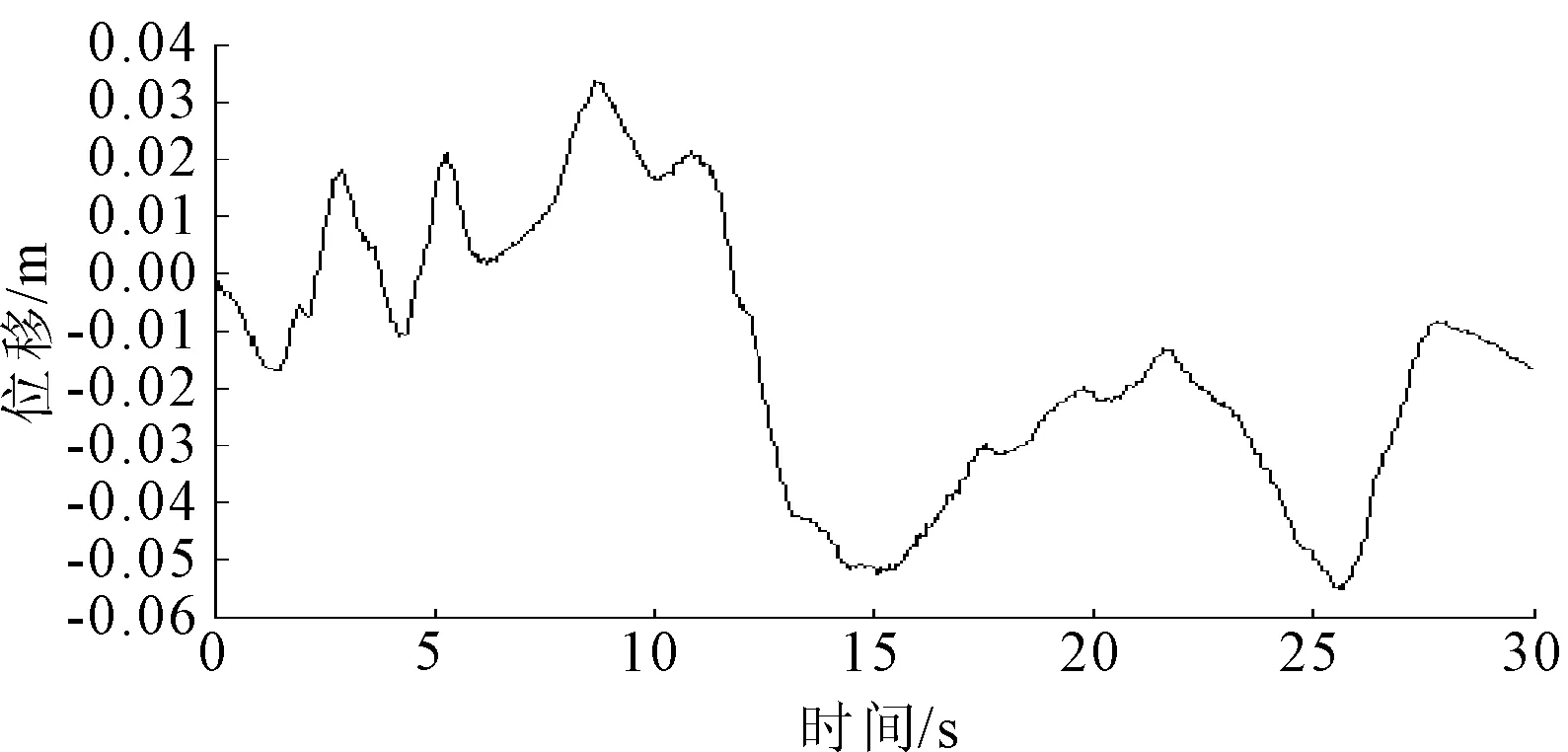
图10EL-Centro波作用下坡顶位移响应时程曲线

4.3不同输入地震动响应

按照本文提出的计算方法，对某垃圾填埋场进行了地震响应分析。由表2可以看出，针对不同地震动的输入，在坡顶处加速度峰值有很大区别，宁河波加速度响应最大，而对于位移响应，迁安波最大。从图11可以看出，不同地震波响应过程也有显著差异，这主要是由于输入地震波频谱特性不同，当地震波的激励频率与填埋场响应频率接近时，引起的响应最大。由图12可以看出，沿填埋场深度方向，加速度响应逐渐减小，四条输入地震波引起的边坡动力响应变化趋势相同，但不同地震波对边坡顶部加速度响应有显著差异，宁河地震波输入响应最大，迁安地震波输入响应最小，反映了输入地震动波的频谱特性对填埋场响应有影响。所以，在对实际填埋场进行地震响应分析时，至少应选择两条实测波加一条人工合成地震波作为输入地震波，这样才能较好反映填埋场动力响应特性。

表2　计算得到的坡顶放大系数

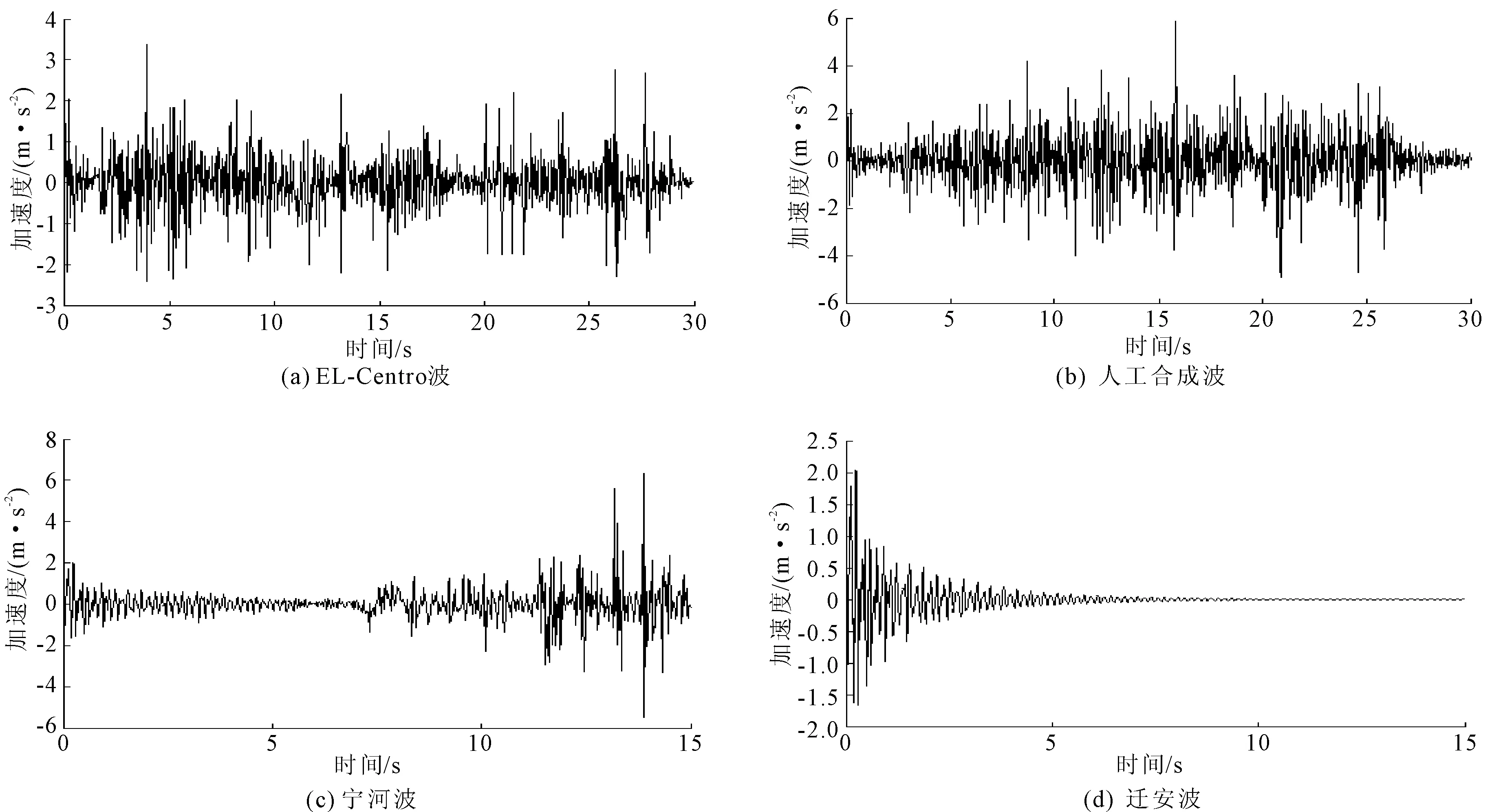
图11不同地震波作用下坡顶加速度响应时程曲线

图12加速度峰值随填埋深度变化曲线

5　结　语

本文基于动力响应时程分析，对某垃圾填埋场进行分析，为了反映不同地震波对填埋场地震动力响应的影响，本研究输入了四条地震波，经分析、比较得到如下结论：

(1)地震波类型对填埋场地震响应有显著差异，在对实际填埋场抗震设计时，至少应选择两条实测波加一条人工合成地震波作为输入地震波，这样才能较好反映填埋场动力响应特性。并在填埋场抗震设计时取各响应量的最大值作为设计控制参数。

(2)造成填埋场动力响应不同的根本原因是输入地震波频谱特性不同，当地震波的激励频率与填埋场的振动频率接近时响应最大。

参考文献：

[1]Kramer S L,Smith M W.Modified Newmark model for seismic displacements of complaint slopes[J].J.Geotech.Engrg.ASCE,1997,123(7):635-644.

[2]邓学晶，孔宪京，刘君.城市垃圾填埋场的地震响应及稳定性分析[J].岩土力学，2007，28(10)：2095-2100.

[3]刘红帅,薄景山，刘德东，等.岩土边坡地震稳定性分析研究评述[J].地震工程与工程振动,2005,25(1):164-171.

[4]周健，贾敏才.固体废弃物堆埋场抗震稳定性研究现状[J].世界地震工程，2001,17(3):38-42.

[5]刘汉龙,费康,高玉峰.边坡地震稳定时程分析方法[J].岩土力学,2004,24(4):553-556.

[6]祁生文.边坡动力响应分析及应用研究[D].北京：中国科学院地质与地球物理研究所，2002.

[7]栾茂田,李湛,范庆来.土石坝拟静力稳定性分析与坝坡地震滑移量估算[J].岩土力学,2007,28(2):224-230.

[8]帅海乐，冯世进，詹黔花，等.垃圾填埋场的地震响应特性分析[J].振动与冲击,2013,32(4):75-79.

[9]张国栋，刘学，金星，等.基于有限单元法的岩土边坡动力稳定分析及评价方法研究进展[J].工程力学，2008，25(A02):44-52.

[10]陈国兴.岩土地震工程学[M].北京：科学出版社，2007.

[11]李勇.城市固体废弃物填埋场边坡地震响应分析[J].水利与建筑工程学报，2010,8(2):30-33.

[12]Kondner R L.Hyperbolic stress-strain response：cohesive soil[J].Journal of the Soil Mechanics and Foundation Division,ASCE,1963,89(S1):115-143.

[13]Hardin B O,Drnevich V P.Shear modulus and damping in soils[J].Journal of the Soil Mechanics and Foundation Division,ASCE,1972,98(7):667-692.

[14]冯世进，陈云敏，孔宪京，等.城市固体废弃物动力特性试验研究[J].岩土工程学报，2005,27(7):750-754.

[15]张国栋，李勇.城市固体废弃物的容重研究[J].环境科学与技术，2008,31(6):204-206.

[16]胡聿贤，何训.考虑相位谱的人造地震动反应谱拟合[J].地震工程与工程振动，1986,6(2):37-51.

[17]赵凤新，张郁山.拟合峰值速度与目标反应谱的人造地震动[J].地震学报，2006，28(4)：429-437.

[18]张锋春，梁力，戴玉买.Ansys在排土场动力时程分析中的应用[J].金属矿山，2009,399(9):160-164.

TimeHistoryAnalysisfortheSeismicResponseofLandfillSlope

LI Yong

(ArchitectureandCivilEngineeringInstitute,GuangdongUniversityofPetrochemicalTechnology,Maoming,Guangdong525000,China)

Abstract：With the acceleration of urbanization and new rural construction process,environmental requirements are also raised.At present,building landfills to dispose of municipal solid waste is still an effective and most commonly used method.Landfill slopes have the same stability problems with other natural and manmade slopes.According to the engineering practice of municipal solid waste landfills,based on the analysis of time history for dynamic response of landfills slope,the equivalent linearization method was used to study the non-linear dynamic response characteristics of the waste in the landfill.In order to fully reflect the impact of the seismic motion characteristics on the dynamic response of the landfill,three actual recorded waves and an synthetic wave were input as seismic motions.The result indicates that there are significant differences on the seimic response of landfills according to the input of different seismic waves.When conducting seismic design of the actual landfill sites,there should be at least 2 actual waves and one synthetic wave as input waves to better reflect the landfill dynamic response characteristics.

Keywords：seismic response;time history;slope;landfill

DOI:10.3969/j.issn.1672-1144.2014.06.020

中图分类号：TU345

文献标识码：A

文章编号：1672—1144(2014)06—0102—05

作者简介：李勇(1980—)，男，湖南岳阳人，硕士，讲师，工程师，主要从事土动力学与环境岩土工程方面的教学与科研工作。

基金项目：茂名市科技计划项目(2012B01077)

收稿日期：2014-08-01修稿日期：2014-09-07