特征序列数据关联机器人同步定位与地图构建*

弋英民,黄 莹,王智敏,张孟志

(西安理工大学自动化与信息工程学院,西安 710048)



特征序列数据关联机器人同步定位与地图构建*

弋英民*,黄 莹,王智敏,张孟志

(西安理工大学自动化与信息工程学院,西安 710048)

针对噪声不确定性增大的数据关联问题,提出特征点序列数据关联机器人同步定位与地图构建方法。根据机器人环境特征点的空间几何信息,基于图论建立特征点间的信息相关性。利用相邻两步的特征点观测信息协方差的变化,转化成求解特征点TSP问题和特征序列最大相关函数,以此确定所观测特征点的数据关联。实验证明,提出的方法可在噪声不确定性增大的情况下,保证同步定位与地图构建算法的一致性。

特征序列;数据关联;同步定位与地图构建;机器人

数据关联方法是机器人的同步定位与地图构建(SLAM)的关键环节。Smith[1-4]等人提出的扩展卡尔曼滤波估计(EKF-SLAM)是解决SLAM问题的基础理论方法。文献[5-6]分析了EKF-SLAM和FastSLAM的一致性估计问题,研究表明数据关联方法直接影响算法的一致性估计精度。数据关联是确定传感器接收到的量测信息与目标源对应关系的过程。文献[5]研究表明数据关联是解决SLAM问题的关键,不正确的数据关联将使构图和机器人的定位估计发散,甚至导致整个SLAM过程失败。机器人SLAM研究所采用的数据关联算法已取得一定成果,主要为三类,一是常用的最近邻数据关联[7];二是概率统计数据关联[8];三是基于图论的相关性数据关联。文献[9]提出的最近邻数据关联(NN),实现简单但抗干扰能力差。概率数据关联PDA方法适用于单目标问题。针对多目标问题的联合概率数据关联(JPDA)因其难以确切得到联合事件与关联事件的概率,并且由于回波密度增加引起组合爆炸,学者提出了折中近似算法。文献[10]提出Takagi-Sugeno数据关联(TSDA),相比JPDA提高了精度,降低了计算复杂度。文献[11]提出了3SCAN-JPDA算法,可用于实时动态环境,降低了算法计算量。文献[12]针对杂乱环境提出一种联合相容分枝定界的数据关联方法JCBB(Joint Compatibility Branch and Bound)。文献[13]为获得较高关联准确率,提出一种基于蚁群、遗传算法的多目标数据关联算法(AC-GADA)。文献[14-16]利用特征点特征、特征点群的布局以及特征点预测与观测的偏差界限等信息,提出了概率数据关联的改进算法。文献[17-18]提出了基于图论的数据关联算法MCS(Maximum Common Subgraph),但是搜索两幅完全图的最大公共完全子图的NP问题困难。MCS和JCBB都利用所有可用的相关信息进行批量数据关联。JCBB通过预设假设并在搜索树上解释这一假设,以最优的解释对应的假设为可信的数据关联;MCS分为两步,首先编制成对约束,之后为最大兼容约束组织搜索。对于JCBB、MCS和NN数据关联方法,在噪声不确定性增大时,由于观测信息和特征点本身相互独立,造成匹配不成功或估计误差增大。

针对系统噪声不确定性增大的情况,利用相邻两个时刻的信息协方差差异,提出一种特征序列数据关联方法(LSDA)。方法要点是:解预测特征点和观测特征点的TSP问题,获取TSP序列,对两组序列求最大相关函数,并标记已观测特征点与新观测特征点,最后进行特征点数据关联,更新地图。

1 特征序列数据关联方法

机器人同步定位与地图构建是以数据关联为基础。针对系统噪声不确定性增大的情况,将求解特征点的TSP问题引入机器人的SLAM问题中,通过计算TSP序列的最大相关函数,获得特征点数据关联,更新地图。

1.1 经典EKF-SLAM方法

基于EKF的机器人同步定位与地图构建方法以最小均方差为准则,实现机器人位姿在时域的最优递推过程。该方法主要分为预测和更新两步。将控制信号或里程计的信息输入到机器人系统的状态方程,完成对位姿和地图特征的预测;通过对环境特征的观测和提取,来更新机器人位姿和特征地图[4]。

预测:

(1)

Pxx,k|k-1=fPxx,k-1|k-1fT+Qk

(2)

更新:

(3)

(4)

其中

Sk=hPk|k-1hT+Rk

(5)

Wk=Pk|k-1

(6)

1.2 基于模拟退火方法的特征点TSP问题

机器人SLAM问题中的特征点可类比成TSP问题中的城市。特征点坐标表示城市所处位置,并可通过坐标计算城市间距离。SLAM问题中,总是假设特征点是静止不动的。因此,特征点TSP问题的最优解是唯一的。由于存在观测噪声,观测区域内的所有特征点作为已有条件定义TSP问题。模拟退火算法特别适合处理全局优化、离散变量优化问题[19-20]。特征点TSP问题的模拟退火方法示意图如图1所示。

图1 基于模拟退火方法的特征点TSP问题

对预测特征点(观测区域的已观测特征点预测)求解TSP问题,得到最优的TSP路径。对观测特征点求解TSP问题,同样可以得到一条最优的TSP路径。

1.3 特征点序列的相关函数

将特征点的坐标看作自变量,特征点就是二维的离散点。根据TSP路径,可以得到一组特征点的排列。每一个排列就是一条特征点序列,即特征点间的连线代表一个固定时间段。序列即信号,最大相关函数所对应的两条特征点序列便可确定公共特征点的关联。

1.4 特征点序列数据关联方法

特征点序列的数据关联方法(LSDA)主要过程是:求解预测特征点和观测特征点的TSP问题,取得TSP序列。对两组序列求最大相关函数,并标记已观测特征点与新观测特征点,最后进行特征点关联,更新地图。

具体步骤如下:

Step 1:初始化,数据关联

预测已观测过的特征点,保留在当前观测区域的已观测特征点,记为预测特征点。

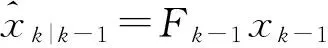
(7)

对特征点进行观测,得到观测特征点。将特征点看作是TSP问题的城市,用特征点坐标表示城市所处位置并计算城市间距离。

Step 2:解特征点TSP问题

对预测特征点和观测特征点两种组合求解特征点TSP问题,得到特征点排列。将特征点排列看作关于坐标的二维序列,得到两组序列。

Step 3:计算序列的相关函数

对特征点坐标的两组序列求相关函数,取最大相关函数对应的序列。根据预测特征点组合获得序列长度,将观测特征点组合序列分为已观测特征点zko和新观测特征点zk,k-1。则

(8)

Step 4:解已观测特征点TSP问题

对已观测特征点求解特征点TSP问题,得到已观测特征点序列排列。

Step 5:计算已观测特征点序列

对已观测特征点序列排列和预测特征点序列求相关函数,取最大相关函数对应的已观测特征点序列。

Step 6:关联地图

将已观测特征点序列和预测特征点序列进行地图构建特征点关联,并在地图中加入新观测特征点。

(9)

为了验证算法的一致性估计问题,假设线性高斯滤波,采用NEES(Normalised Estimation Error Squared)来评价滤波估计的性能指标[21],即

(10)

(11)

2 实验及分析

图2是MT-R机器人实验验证平台,为两轮驱动的MT-R移动机器人,配备有两自由度云台摄像机、超声波传感器和测速编码器等传感器。在实验中,记机器人位姿为(x,y,θ)T,分别对应平面坐标(x,y)和方向角θ。

图2 实验验证平台

实验对几种典型数据关联方法进行对比分析。将NN、JCBB和LSDA方法分别应用到机器人SLAM。第一组低噪声实验初始条件为P0=diag[1e-4,1e-4,1e-4],Q0=diag[0.32,(3.0*pi/180)2],R=diag[0.12,(1.0*pi/180)2]。第二组高噪声实验初始条件为P0=10*diag[1e-4,1e-4,1e-4],Q0=10*diag[0.32,(3.0*pi/180)2],R=10*diag[0.12,(1.0*pi/180)2]。

实验是噪声不确定性增大时几种数据关联方法的机器人SLAM实验数据。*表示地图中的特征点。+表示地图中的特征点预测位置,用椭圆表示特征点预测位置区间。线段表示方向点连线。曲线表示机器人实际路径。图3(a)是采用NN数据关联的机器人SLAM构图,图3(b)是采用NN数据关联的机器人SLAM局部放大图;图4(a)是采用JCBB数据关联的机器人SLAM构图,图4(b)是采用JCBB数据关联的机器人SLAM局部放大图;图5(a)是采用LSDA数据关联的机器人SLAM构图,图5(b)是采用LSDA数据关联的机器人SLAM局部放大图。

图3 高噪声时NN-SLAM实验

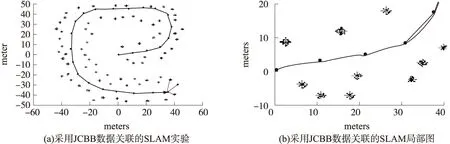
图4 高噪声时JCBB-SLAM实验

图5 高噪声时LSDA-SLAM实验

从图5相比图3和图4可以看出,采用NN数据关联和JCBB数据关联方法机器人构建的地图中,估计值与实际值有一定的偏差;而采用LSDA数据关联的机器人SLAM构建的地图中,估计值与实际特征点位置基本重合。表明提出的方法优于最近邻数据关联和JCBB数据关联方法。

为验证提出方法的一致性估计问题,对三种方法采用50次实验,比较在不同噪声条件下机器人位姿的一致性估计。图6是在低噪声条件下采用三种数据关联方法的机器人位姿的NEES的实验数据。

从图6可以看出,在低噪声条件下,采用NN数据关联、JCBB数据关联的机器人位姿的NEES曲线大部分不在置信区间内,可认为是保守估计;采用LSDA数据关联方法的机器人位姿的NEES曲线大部分在置信区间内,可认为是乐观估计。

图7是在高噪声条件下采用三种数据关联方法的机器人位姿的NEES的实验数据。

图6 低噪声下数据关联方法的一致性估计

从图7可以看出,在高噪声情况下,采用NN数据关联、JCBB数据关联的机器人位姿的NEES曲线局部剧烈震荡,大部分不在置信区间内,可认为是保守估计;采用LSDA数据关联方法的机器人位姿的NEES曲线大部分在置信区间内,可认为是乐观估计。

图7 高噪声下数据关联方法的一致性估计

综上实验结果,所提出的方法在噪声不确定性增大的情况下,机器人SLAM算法仍可保持乐观的一致性估计,提出的方法总体上优于NN数据关联和JCBB数据关联方法。

3 总结

针对机器人SLAM系统噪声不确定性增大的情况,提出了一种特征点序列数据关联的机器人同步定位与地图构建方法。利用类比城市间的TSP问题,求解特征点的相关函数进行观测和预测特征点的数据关联,并更新地图。通过在机器人实验平台测试表明,提出的机器人特征序列数据关联方法可在系统噪声不确定性增大的情况下,保证算法是乐观的一致性估计。

[1] Uyen H S V,Jeon J W. Combine Kalman Filter and Particle Filter to Improve Color Tracking Algorithm[C]//Proceedings of International Conference on Control,Automation and Systems 2007,2007:558-561.

[2]Anati R,Scaramuzza D,Derpanis K G,et al. Robot Localization Using Soft Object Detection[C]//2012 IEEE International Conference on Robotics and Automation(ICRA). 2012:4992-4999.

[3]Ivanjko E,Uasak M,Petrovic I. Kalman Filter Theory Based Mobile Robot Pose Tracking Using Occupancy Grid Maps[C]//International Conference on Control and Automation(ICCA2005),2005:869-874.

[4]Smith R,Chesseman P M. Estimating Uncertain Spatial Relationships in Robotics[J]. Ulncertainty in Artificial Intelligence,1988(2):435-461.

[5]Bailey T,Nieto J,Guivant J,et al. Consisteney of the EKF-SLAM Algorithm[C]//IEEE/RSJ Int Conf on Intelligent Robots and Systems. Beijing:IEEE,2006:3562-3568.

[6]Bailey T,Nieto J,Nebot E. Consistency of the Fast SLAM Algorithm[C]//Proc IEEE Int Conf on Robotics and Automation. Orlando:IEEE,2006:424-429.

[7]弋英民,刘丁. 有色过程噪声下的轮式机器人同步定位与地图构建[J]. 电子学报,2010,38(6):1339-1243.

[8]李辉,张安,沈莹,等. 基于交互式自适应概率数据关联的目标跟踪算法[J]. 传感技术学报,2007,20(1):172-176.

[9]Singer R A,Sea R G. A New Filter for Optimal Trackingin Dense Multitarget Environments[C]//Proceedingss of Theninth Allerton Conference Circuit and SystemTheory. Urbana-Champaign,USA. 1971:201-211.

[10]Watanabe K,Pathiranage C D,Izumi K. T-S Fuzzy Model Adopted SLAM Algorithm with Linear Programming Based Data Association for Mobile Robots[C]//ISIE 2009. IEEE International Symposium on Industrial Electronics,IEEE,2009:244-249.

[11]Wong R H,Xiao Jizhong,Joseph S L. A Robust Data Association for Simultaneous Localization and Mapping in Dynamic Environments[C]//2010 IEEE International Conference on Information and Automation(ICIA),IEEE,2010:470-475.

[12]Neira J,Tards J D. Data Association in Stochastic Mapping Using the Joint Compatibility Test. IEEE Transactions on Robotics and Automation,17(6):890-897,2001.

[13]袁述,袁东辉,孙基洲,等. 蚁群-遗传算法在多传感器多目标跟踪技术中的应用[J]. 电子学报,2013,41(3):609-614.

[14]Maksarov D,Durrant-Whyte H. Mobile Vehicle Navigation in Unknown Environments:A Multiple Hypothesis Approach[J]. IEEE Proc:Control Theory Application,1995,142(4):385-391.

[15]Guivant J,Nebot E. Optimization of the Simultaneous Localization and Map-Building Algorithm for Real-Time Implementation[J]. IEEE Transactions on Robotics and Automation,2003,17(3):242-257.

[16]Castellanos J A,Montiel J M M,Neira J,et al. The SPmap:A Probabilistic Framework for Simultaneous Localization and Map Building[J]. IEEE Transactions on Robotics and Automation,1999,15(5):948-952.

[17]Bailey T,Nebot E. Localisation in Large-Scale Environments[J]. Robotics and Autonomous Systems,2001,37(4):261-281.

[18]Bailey T,Nebot E M,Rosenblatt J K,et al. Data Association for Mobile Robot Navigation:A Graph Theoretic Approach[C]//In IEEE International Conference on Robotics and Automation,volume 3,2000:2512-2517.

[19]Jeong C S,Kim M H. Fast Parallel Simulated Annealing for Traveling Salesman Problem[C]//IJCNN International Joint Conference. San Diego,CA. 1990:947-953.

[20]李芳芳,王靖. 一种基于模拟退火算法的无线传感器网络最优簇类求解方案[J]. 传感技术学报,2011,24(6):900-904.

[21]Bar-Shalom Y,Li X R,Kirubarajan T. Estimation with Applications to Tracking and Navigation[M]. Toronto:John Wiley and Sons,2001:234-235.

弋英民(1976-),1998年于西安交通大学获得学士学位,2004年于西安交通大学获得硕士学位,现为西安理工大学副教授,研究方向为机器人同步定位与地图构建,yiym@xaut.edu.cn。

LandmarkSequenceDataAssociationMethodforRobotSimultaneousLocalizationandMapBuilding*

YIYingmin*,HUANGYing,WANGZhimin,ZHANGMengzhi

(Faculty of Automation and Information Engineering,Xi’an University of Technology,Xi’an 710048,China)

For the noise uncertainty increases,a landmark sequence data association(LSDA)method for robot simultaneous localization and map building(SLAM)is proposed. As robot simultaneous localization and map building,the spatial geometry of the landmarks are considered. Then the correlation among landmarks based on graph theory is established. Between the adjacent two-step observations,the difference of innovation covariance is transformed into maximum correlation function of sequence by solving the TSP problem. Then landmark data association is performed. The experiments show that the proposed method can be to ensure the consistency of estimation in the case of uncertainty noise increasing.

landmark sequence;data association;simultaneous localization and mapping;robot

项目来源:国家自然科学基金项目(51275405);陕西省教育厅自然科学专项项目(2013Jk1078)

2014-07-10修改日期:2014-09-05

10.3969/j.issn.1004-1699.2014.11.014

TP24

:A

:1004-1699(2014)11-1517-05