一种MEMS水听器信号去噪的组合算法研究*

梁 斌,王 鹏,2,白艳萍*

(1.中北大学理学院数学系,太原 030051;2.中北大学微米纳米技术研究中心,太原 030051)



一种MEMS水听器信号去噪的组合算法研究*

梁 斌1,王 鹏1,2,白艳萍1*

(1.中北大学理学院数学系,太原 030051;2.中北大学微米纳米技术研究中心,太原 030051)

针对MEMS水听器采集的数据“淹没”在强噪声场中的问题,提出采用LMS自适应噪声对消与Fourier变换滤波相结合的组合算法实现MEMS水听器的信噪分离。在信号频率已知的情况下,设计了一种自适应噪声对消和Fourier变换滤波组合算法的滤波器,对提取后的信号与理想信号做性能对比。仿真实验表明:该组合算法在-15 dB的强噪声场中仍有较高的分辨精度和提取效果,对搜寻类似于“黑匣子”等情况比较适宜,并将设计的滤波器用于中北汾机测试实验的信噪分离中,结果验证了该算法具有良好的高效性和实用性。

MEMS水听器;信噪分离;LMS自适应噪声对消法;快速Fourier变换

马航空难发生后,牵动了全世界的心,除了各种救助打捞遇难者行动外,人们最为关注的就是寻找飞机的“黑匣子”[1-4]。“黑匣子”是飞行参数记录系统的俗称,当飞机发生事故时,其飞行数据手机转置可以从飞机上的各个传感器和发射场取得诸多重要数据,飞行记录仪提供的证据,可以揭示某一个或若干个事故的因素,给人们提供分析研究的依据,以便对事故做出正确的结论,改进飞行安全制度,提高飞行安全质量,保障人民的生命安全。马航的黑匣子装有水下定位信标(ULB),定位信标入水被激活,发出37.5 kHz的脉冲信号,能从深4 267 m的水下传递声音,并可连续工作至少30 d。但是由于海上波浪翻滚,兼之海洋环境噪声比较复杂多变,信标发出的信号变得很微弱。因此,关于水声微弱信号[1,5]的信噪分离就变得相当重要。目前,比较经典的去噪方法都会有其局限性,比如盲源分离对于非线性问题的普遍适用算法还力有未逮;小波去噪不能同时获取任意多尺度的分辨率,小波基的选取没有适用规律,阈值调整受主观影响很大[6-7];传统的自适应噪声对消法ANC(Adaptive Noise Cancellation)在低信噪比(低于0 dB)和非平稳噪声环境下去噪效果很差[8-10]。因此国内外的许多研究学者进行了很多的算法改进[11-12]。

鉴于信号的频率已知,本文采用基于噪声和信号交叉验证的LMS自适应噪声对消和Fourier变换[13-14]组合算法来提取有用信号,并对该组合算法提取结果做性能对比[7]。仿真结果发现该组合算法突破了传统自适应噪声对消法在低信噪比(低于0 dB)和非平稳噪声环境下去噪效果奇差的局限,将最低适用信噪比降至-15 dB。

本文汾河晋机实验中验证了该算法的实用性:发射模拟信号,频率已知,采集信号经Butterworth带阻数字滤波器经行粗略滤波,得到噪声参考信号,再经自适应噪声对消滤波及Fourier变换滤波后,得到实际信号的最佳估计。

1 LMS自适应噪声对消法和Fourier变换的原理及算法

1.1 LMS自适应噪声对消原理及算法

自适应噪声对消系统是根据参考噪声与信号中干扰噪声的相关性,采用自适应算法[9-10]利用滤波器将信号中的噪声进行对消,而最小均方误差LMS(Least Mean Square)就是以期望信号与滤波器输出信号之间误差的均方值最小为准则,根据输入信号在迭代过程中估计梯度矢量,更新权系数获取最佳的自适应迭代算法。

设自适应滤波器在i时刻的抽头输入X(i)=[x(i),x(i-1),…,x(i-L+1)]T,W(i)=[w1(i),w2(i),…,wL(i)]T,L为滤波器的阶数,Wi(i)为初始随机权值,则:

e(i)=d(i)-WTX
W(i+1)=W(i)+2μe(i)X(i)

(1)

其中,μ为步长参数,决定着算法的收敛速度和达到稳态时失调量的大小,μ值越大,收敛速度越快,但是失调量也变大,稳定性变差,反之亦然。

1.2 Fourier变换原理及算法

对于平稳信号,Fourier变换具有很好的分析效果,它反映的是信号在整个时间段的特征。在频率域内,该方法检测各次稳态谐波的幅值和频率。

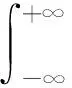
(2)

F(ω)呈现离散状态,其中ω=2π/T,T为f(t)的周期。若将f(t)离散化,每隔T/N时间间隔采样,采样点数(快拍数)为N,则有

(3)

写成矩阵形式如下

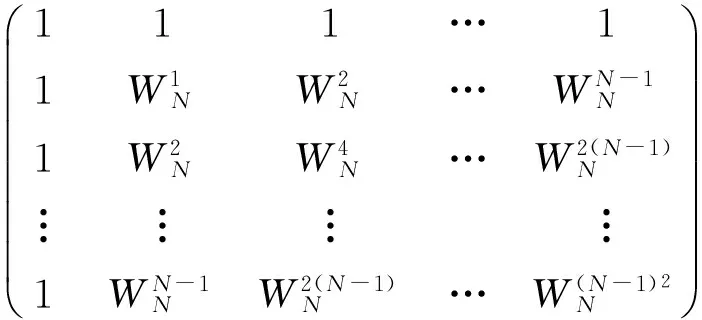
(4)

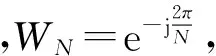
本文设计了一种基于噪声和信号交叉验证的自适应噪声对消和Fourier变换组合滤波器,结构如图1所示。

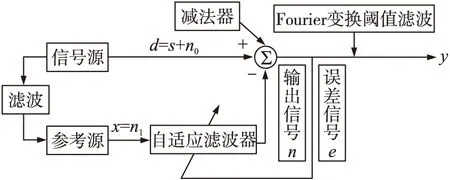
图1 基于噪声和信号交叉验证的自适应噪声对消法和Fourier滤波组合原理图

在图1中,观测信号d包含有用信号s和噪声信号n0,且有用信号s与噪声信号n0不相关。鉴于有用信号的频率已知,设计Butterworth带阻数字滤波器[13],滤波后得到信号作为参考源的参考信号n1,则n1与s无关但和n0相关。参考信号n1经过自适应滤波器滤波达到稳定后,输出信号n作为n0的最佳逼近,得到的误差信号e就是有用信号s的最佳估计,算法[9]如下:

误差信号:

e=d-n=s(i)+n0(i)-n1(i)

(5)

对上式(5)两边平方取期望,由于信号和噪声的独立无关性,得

E[y2]=E[s(i)2]+E[(n0(i)-n1(i))2]+
2E[s(i)(n0(i)-n(i))]=E[s(i)2]+
E[(n0(i)-n(i))2]

(6)

当E[(n0(i)-n(i))2]最小时,则误差信号e就是有用信号s的最佳估计。

2 仿真实验

本文所用软件为MATLAB 2014a,有用信号是一列正弦信号(s=a·sin(2π·400·t),a为有用信号的幅值,频率为400 Hz)。观测信号可由不同分贝的高斯白噪声和有用信号叠加而成,分贝越低,噪声越多,当分贝达到-10 dB时,噪声与信号的功率谱比值达到10∶1,属于强噪声场。本文以-10 dB为例,有用信号s与观测信号d分别入图2所示。

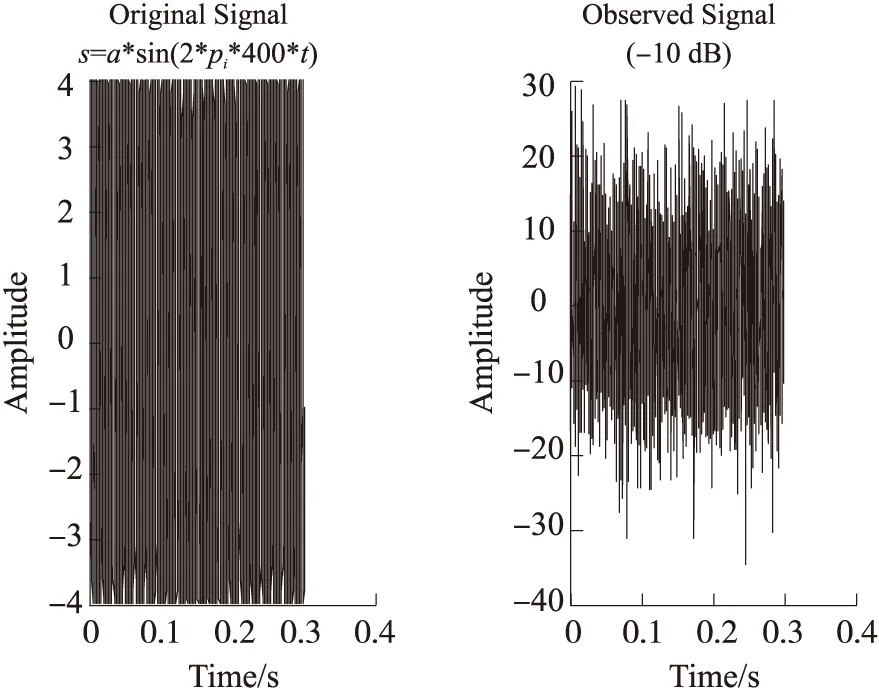
图2 有用信号s与观测信号d图

本次仿真程序中,采集频率为10 kHz,快拍数为3 000,加噪-10 dB,已知信号的频率400 Hz,设计Butterworth带阻数字滤波器(Rp=1 dB,Rs=20 dB),可得到噪声参考信号作为自适应滤波器的输入信号,仿真程序结果如图3所示。

图3 自适应滤波图

在图3中,子图1是有用信号波形图,子图2是加噪-10 dB后的观测信号波形图,子图3是自适应滤波后的信号波形图。对子图3的信号做Fourier变换滤波,由于初步提取的信号中有用信号的能量占明显优势,故选取合适的幅值系数阈值,低于阈值的全部置换成零,再经过Fourier逆变换得到信号的时域波形图,程序结果如图4所示。

对上述实验重复经行500次,做去噪性能分析对比[6-7],评价参数为均方误差(RMSE)、信噪比(SNR)、信噪比增益(GSNR)、相似度(R)。在本文中,信噪比增益为去噪后信噪比减去去噪前信噪比。因此均分误差越小,信噪比及信噪比增益越高,相似度越高,则说明去噪性能越好,不同加噪分贝下性能对比如表1所示。

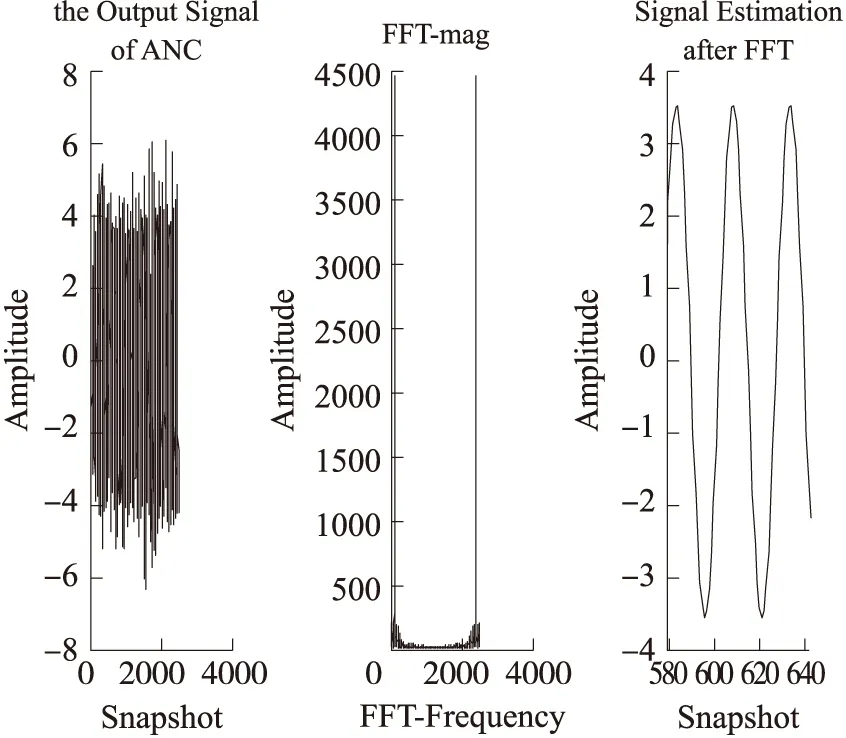
图4 Fourier变换滤波图

表1 强噪声环境下信号提取效果性能对比表

由表1可知,在强噪声-15 dB左右时,本文的算法具有很好的去噪性能,突破了以往自适应滤波只能在0 dB以上的平稳噪声场中使用的限制。但是,在噪声更强烈的情况下,比如超过-20 dB以上,均方误差急剧变大,相似度急剧变小,甚至计算机没法计算出精确解,出现“NaN”,这说明该算法在超强噪声场中的微弱信号提取效果会变的很差,收敛精度也很低,说明了自适应滤波在更强的噪声场中受影响很大。

3 湖试实验处理

中北大学自主研制的MEMS矢量水听器,是将MEMS技术应用[15-16]与水听器技术相结合的一种创新尝试。该水听器设计灵感来源于鱼的侧线感知系统,依据介观压阻效应和声学柱体的同振原理,以量子阱薄膜为敏感单元,并采用微纳结合的纤毛式水声矢量探测仿生结构,声波引起纤毛式声学柱体的振动,使四梁微结构内部产生形变,引发纳机电敏感单元共振隧穿电流变化,产生介观压阻效应,通过检测系统提取电阻的变化,从而实现水下声信号的探测。该MEMS矢量水听器经中船重工715所水声国防一级计量站标定测试,灵敏度高达-184.6 dB(0 dB=1 V/μPa),频率响应范围为5 Hz～5 kHz,且具有良好的“8”字型余弦指向性[17]。

2011年10月,中北大学微米纳米技术研究中心在汾河二库进行了汾机实验测试,实验流程如下:将水听器阵列(MEMS矢量水听器4元线阵,间距1 m)置于岸边固定,换能器置于拖船上,拖船离阵列距离逐步加大,选择不同位置抛锚不动,利用换能器发射信号,进行数据采集。本次数据处理选取fenji331 Hz数据包,声源距离水听器6 m,发射信号频率为331 Hz,采样频率为10 kHz,图5为1#矢量水听器第二路(Y路)原始采集数据。

图5 单个水听器原始信号图

在本次湖试实验中,信号的信噪比大致在-10 dB左右,该算法具有很高的精度和提取效果,实验数据处理流程如下:

①根据信号频率设计Butterworth带阻滤波器

得到噪声的先验知识,作为自适应滤波器的参考输入信号,调整更新权值参数,得到原始信号和初步提取信号对比图,采样点从第40 000个到第45 000个,结果如图6、图7所示。

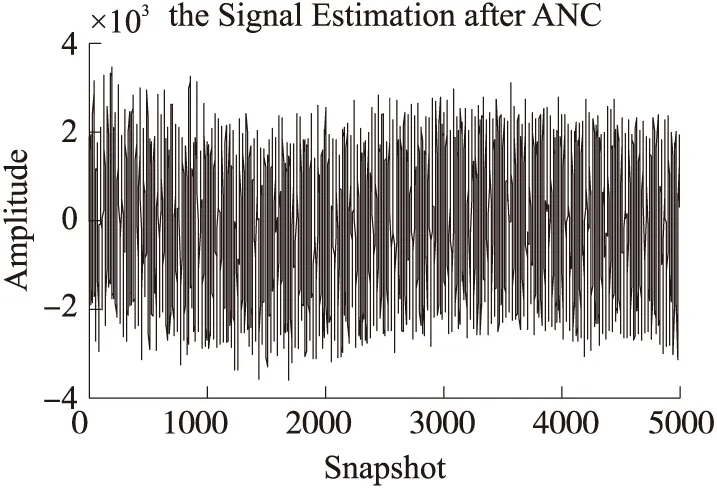
图7 自适应初步提取信号图

②再对初步提取信号从第1001个点到第5 000个采样点做Fourier变换阈值调整,系数幅值低于阈值(这路信号阈值取1.5)的全部归零,然后进行Fourier反变换,得到的信号就是有用信号的最佳估计,结果如图8所示。

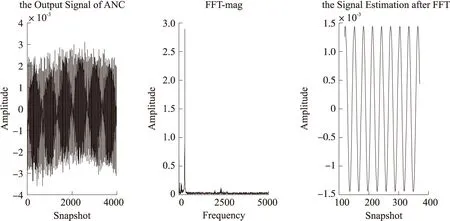
图8 初步提取信号经Fourier变换滤波后对比图

4 结论

信号的频率已知,依据数字带阻滤波器得到噪声的先验知识进行自适应噪声对消处理得到初步提取信号,再根据Fourier变换幅值系数阈值调整对初步提取信号滤波处理,反变换得到有用信号的最佳估计,从而达到从强噪声场中提取微弱信号的目的。仿真实验和二库湖试实验都验证了该算法的优越性和实用性。在本文中,着重考虑的是MEMS矢量单频信号的分离去噪,对于多频信号以及相干信号的分离去噪,在笔者的另外一篇论文中会有深入的探讨。

[1] 程道来,仪垂杰,张志强,等. 飞机黑匣子舱音背景声特征识别体系建立的探讨[J]. 中国民航飞行学院学报,2009,20(6):11-15.

[2]James R Cash. Group Chairman’s Report of Inverstigation Sound Spectrum Study of Cockpit Voice Recorder[R]. American Arilines Flight 587,DCA02MA001. Belle Harbor,NY November 12,2001.

[3]James R Cash. Group Chairman’s Factual Report Sound Spectrum Study of Cockpit Voice Recorder[R]. DCA001MA006. Washington D C,July 31,2000.

[4]James R Cash. Factual Report of Inverstigation Cockpit Voice Recorder[R]. DCA96MA-070. Washington D C,October 20,1997.

[5]李启虎. 水声信号处理领域新进展[J]. 应用声学,2012,31(1):1-9.

[6]张晓宁. 基于小波变换的语言信息去噪算法研究[D]. 河南工业大学,2013.

[7]陶珂,朱建军. 小波去噪质量评价方法的对比研究[J]. 大地测量与地球动力学,2012,32(2):128-133.

[8]梁炎明,刘丁,赵跃. 基于自适应噪声抵消的CZ单晶炉炉膛温度信号处理[J]. 控制理论与应用,2011,28(1):94-100.

[9]张会先. 自适应滤波算法的研究与应用[D]. 西安:西安电子科技大学,2012.

[10]王晓东,王成,贾继鹏,等. 基于改进的NLMP的自适应脉冲噪声对消器[J]. 计算机仿真,2010,27(5):13-15,61.

[11]Dalgaard E,Auken E,Larsen J J. Adaptive Noise Cancelling of Multichannel Magnetic Resonance Sounding Signals[J]. Geophysical Journal International,2012,191:88-100.

[12]Chunshien Li,Tsunghan Wu,Feng-Tse Chan. Self-Learning Complex Neuro-Fuzzy System with Complex Fuzzy Sets and Its Application to Adaptive Image Noise Canceling[J]. Neurocomputing,2012,94(5):121-139.

[13]张德丰. 详解MATLAB数字信号处理[M]. 北京:电子工业出版社,2010:118-142.

[14]Oran Brigham E. Fast Fourier Transform[M]. Shanghai:Shanghai Science Press,1979:11-223.

[15]汪明,陈建辉,王广龙,等. 基于数字式MEMS声传感器阵列的声源定位系统设计[J]. 传感器技术学报,2013,26(8):1105-1109.

[16]孙伟,李婉秋,初婧,等. 基于误差修正技术的井下人员MEMS定位方法[J]. 传感器技术学报,2014,27(7):898-904.

[17]王鹏. 基于MEMS矢量水听器阵列的声目标定向定位技术研究[D]. 太原:中北大学仪器与电子学院,2013.

梁斌(1988-),男,山西平遥人,在读研究生,主要研究方向为传感器信号处理,18203416228@163.com;

白艳萍(1962-)女,山西省太原市,教授,博士生导师,主要研究方向现代优化算法,信息处理与非线性系统建模,baiyp666@163.com。

ACombinationAlgorithmforMEMSHydrophoneSignalandNoiseSeparation*

LIANGBin1,WANGPeng1,2,BAIYanping1*

(1.Faculty of science,Department of maths,North University of China,Taiyuan 030051,China;2.Micro and Nano Technology Research Center,North University of China,Taiyuan 030051,China)

In the light of the problem of MEMS hydrophone data “submerged” in strong noise field,the combination filter of LMS adaptive noise cancellation and Fourier transform filtering is proposed. The filter algorithm is applied to MEMS hydrophone signal and noise separation. When the frequency of signal is given,the combination filter algorithm is used for signal extraction and the ideal signal performance comparison. Simulation results show that the effect of extraction resolution in strong noise field of-15 dB is higher in the algorithm. The algorithm can be used to search similar to the “black box” case. The filter is used to separate signal and noise in the Fen machine test of North University of China. The results show that the algorithm is efficient and Practicability.

MEMS hydrophone;signal-noise separation;LMS adaptive noise cancellation;fast Fourier transform

项目来源:国家自然科学基金项目(61275120)

2014-06-04修改日期:2014-09-22

10.3969/j.issn.1004-1699.2014.11.006

TP274

:A

:1004-1699(2014)11-1477-05