用于1010-6 N～10-5 N微力测量的柔性铰链机构设计*

蔡 雪,赵美蓉,郑叶龙,张国强

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)



用于1010-6N～10-5N微力测量的柔性铰链机构设计*

蔡 雪,赵美蓉*,郑叶龙,张国强

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)

在基于静电场原理的微纳力值测量系统中,力值的传递与转化机构起着至关重要的作用。选择平行四边形柔性铰链机构作为其弹性元件,以实现10-6N量级的力值测量。分析了柔性铰链的数学模型,研究了其静态与动态刚度;根据系统要求确定了柔性铰链的目标刚度,并采用有限元方法对其进行优化设计和模态分析;分析了加工精度对铰链刚度的影响。将该铰链用于微力测量系统中,通过实验给出了刚度测试结果和力值测量结果,实验表明,该平行四边形柔性铰链满足微力测量系统对10-6N量级的力值测量要求。

微力测量;柔性铰链;有限元;刚度

现阶段,微纳量级的力值已越来越多的应用于新材料、生物医药、微电子、航空航天、国防等诸多领域,但目前国际上对于小于10-5N量级的力值计量尚无统一的方法[1-2]。为了促进相关领域的关键技术提升,各国对于微纳力值的计量方法纷纷展开研究。

在微力测量系统中,将微小力值转化成可溯源标准量并将其输出的传递机构是影响力值测量的关键环节,它并不直接参与到力值的计算中,但却决定了测量系统能够达到的力值测量水平。在10-6N量级的力值测量系统中,要求力值传递机构具有较高的灵敏度和重复性精度,适宜的自由度限制以及良好的动态特性。柔性铰链机构因其无摩擦,体积小,无间隙和运动平稳的特点而备受青睐,如美国国家标准技术研究所的静电力一级标准机[3-4],韩国计量院的纳米力校准仪[5],台湾工业技术研究院的竖直式微小力计量装置[6-7]都选用了柔性铰链机构作为其力值的传递机构。但美国和韩国的微力测量系统中的铰链结构相对复杂,且刚度值较大,而台湾的微力测量系统中的铰链结构长期处于悬垂状态,易产生塑性变形,对铰链的长久使用不利。

本文以静电场微小力测量装置为基础,提出并设计了一种应用于微力计量的平行四边形柔性铰链,并在传统的铰链基础上对其进行了相应的优化设计,使其满足测量10-6N～10-5N力值的测量系统要求。

1 微力测量系统的结构及原理

微力测量系统的结构如图1所示。

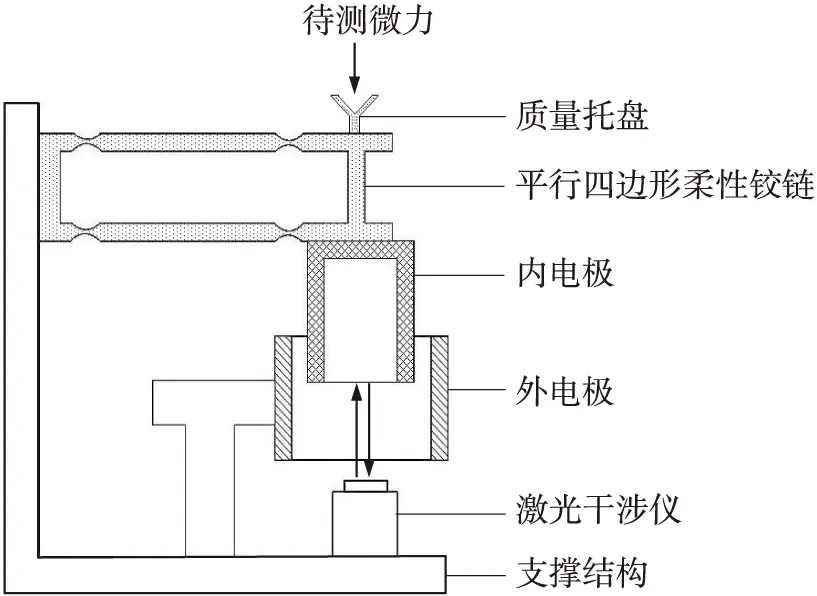
图1 微力系统结构图

该系统基于静电场原理,采用变面积型同轴圆柱电容传感器,将内电极固定于平行四边形柔性铰链一端,外电极固定。当质量托盘上施加了待测量的微小力时,柔性铰链会带动内电极沿竖直方向运动,该运动的位移量可由高精度的激光干涉仪检测得到。根据静电场原理[8-9],当在内外电极之间施加电压时,两电极之间会产生沿内外电极轴线方向的静电力,静电力与电压之间的关系为:

(1)

其中U为内外电极之间的电压,Fe为静电力,dC/dz为内外电极电容梯度,其中dz为内外电极之间的相对位移,dC为两电极之间相对移动dz位移后的电容值变化量,可由高精度电容电桥测得。

在静电力的作用下,内电极会向反方向运动,通过调整电压值U,可保持内电极在平衡位置,通过记录此时的电压值,代入式(1)即可计算得到与待测微小力值相等的静电力值,从而实现微小力值测量。

2 平行四边形柔性铰链设计

2.1 柔性铰链的运动分析

在本测量系统中,平行四边形柔性铰链机构不仅是将待测微力值转化成位移输出的弹性元件,又是支撑内电极和承载待测微力的承载部件。

平行四边形柔性铰链在受力后的运动如图2所示,其特有的平行四边形结构可使运动过程中端部始终处于水平状态,这就保证了内电极的轴线能始终处于竖直状态,因而静电力也沿竖直方向。由于测量时只须关注内电极运动回初始平衡位置时的电源电压值,因此在加载时铰链端部的微小水平位移不会对测量结果造成影响。

图2 平行四边形铰链示意图

对于单个铰链而言,目前典型的有直梁型、圆弧型、椭圆型等。相比较而言,圆弧型铰链的转动精度最高,其次是椭圆型铰链,最后是直梁型铰链。若应用于平行四边形柔性机构,转动精度越高的铰链单元,可使铰链端部的直线位移精度也越高。然而,在最薄处厚度相同时,在改变同样大小力矩的情况下,椭圆形柔性铰链转角偏移量最大,灵敏度最高,适合精度要求较高的场合[10]。在本文的测量系统中,由于测量的力值很小(10-6N量级),对于铰链的灵敏度要求极高,因此综合转动精度与灵敏度的性能,选用椭圆形柔性铰链作为平行四边形机构的基础单元。

2.2 柔性铰链的刚度

2.2.1 刚度计算公式

静载荷下抵抗变形的能力称为静态刚度,动载荷下抵抗变形的能力称为动态刚度。在微力测量系统中,施加的待测微力可认为是静载荷,而外界振动的激励则为动载荷。

①静态刚度

平行四边形柔性铰链的结构如图3所示。

图3 铰链参数

其中,t为铰链最薄处的厚度,b为铰链的宽度,R为椭圆的长轴半径,r为椭圆的短轴半径,H为铰链厚度,l为平行四边形铰链的有效长度。则单个铰链转动刚度[11]:

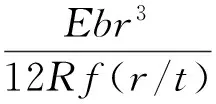
(2)

(3)

而平行四边形机构的静刚度与铰链的转角刚度之间的关系为[12-13]:

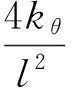
(4)

于是平行四边形机构的静刚度为:

(5)

在本系统中,铰链的整个运动过程可认为是准静态过程,因此可依据静态刚度公式来分析铰链在施加待测微力后的变形。

②动态刚度

为研究平行四边形机构的动刚度,可将其模型简化成质量—弹簧—阻尼二阶系统,如图所4示。

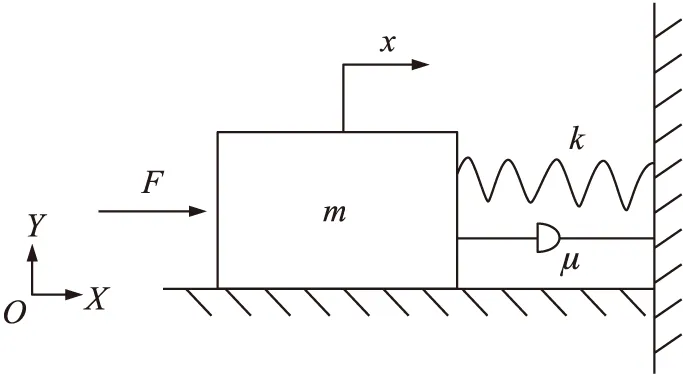
图4 简化的二阶系统

若输入的力值F以频率ω正弦变化,设其为fsinωt,则力的平衡方程为:

(6)

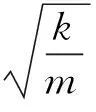
(7)

对式(7)进行傅里叶变换得到其幅频特性为:

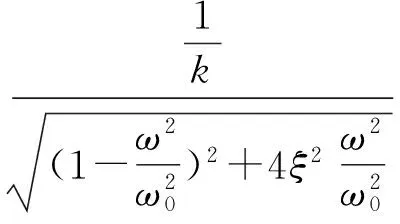
(8)

其中,ω为输入信号的频率,ω0为铰链系统固有频率,ξ为系统的阻尼比,k为系统静刚度。

由于铰链自身结构产生的阻尼相比环境阻尼很小,可认为平行四边形柔性铰链对于动态输入信号的放大作用,只与铰链的静态刚度和信号频率有关,而与铰链的形状参数无关。

由式(8)可知,环境振动对于柔性铰链的运动影响很大,应将微力测量系统置于隔振台上,以减小环境振动对于铰链造成的影响。

2.2.2 刚度选择及参数确定

在该系统中,平行四边形铰链的刚度是一个重要参数。在铰链上施加的静态力F,铰链的输出位移x,以及铰链刚度k三者之间的关系为:

(9)

选用分辨力为1 nm的激光干涉仪作为位移测量器件,测量低至10-6N量级的微力时,刚度值越小,在施加微力后,铰链末端的输出位移越大,力值测量的精确度越高。但过小的刚度要求铰链最薄处的厚度很小,作为内电极支撑结构的铰链,其强度就会得不到保证。同时,在实验室环境中,不可避免的会存在地面、实验台振动,以及其他各种环境干扰,一旦铰链刚度过小,系统的稳定性就会降低,地面振动对实验结果的影响会被放大,因此合理的选择刚度值是至关重要的。

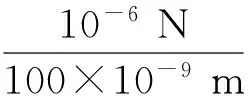
由于平行四边形柔性铰链的刚度较小,且作为内电极的导电器件之一,要求其材料具有较小弹性模数和较好的导电性能。因此选用通用性很强的铝合金作为铰链材料,铝合金材料易加工,质量轻,其抗拉屈服强度σs=280 MPa,杨氏模量E=7.1×1010Pa。

上文已经确定了铰链的目标刚度为5 N/m,以式(5)为依据选择铰链参数:t=0.1 mm,b=5 mm,l=96 mm,R=15 mm,r=5 mm。

2.2.3 加工精度对于铰链刚度影响

由式(5)可知,影响其刚度的参数主要是:铰链的宽度b、切口处的长轴半径R、短轴半径r、最薄处厚度t、铰链的有效长度l。在这些参数中t是影响铰链刚度误差的最主要因素[14],且t的绝对值远小于其他尺寸,是机械加工的最难点,因此这里主要讨论t的尺寸精度对于铰链刚度的影响。

目前机械加工厂对铰链最薄处的加工精度为0.1±0.005 mm。根据式(5)可得到t值在0.1 mm附近变化时,铰链的整体刚度值k的变化范围如图5。

经计算得,当t值从0.095 mm到0.105 mm范围内变化时,铰链刚度从4.447 6 N/m到5.670 7 N/m的范围内变化。因此铰链加工完成后,需先对铰链的刚度进行标定,然后才能用于微小力值测量。

图5 铰链加工精度对于刚度的影响

3 柔性铰链的优化设计

3.1 减重

由上一节可知,铰链薄壁处的最小尺寸只有0.1 mm,但铰链作为内电极的支撑要一直承受铰链本身及内电极的重力,同时铰链还要承受施加的待测微力,长期使用,必然会造成铰链薄壁处的塑性变形,影响测量系统的精度,因此合理的减轻铰链自身重量是一个必要问题。

由平行四边形铰链的原理分析可知,其工作的有效变形区域只有四个椭圆形铰链处,其他部分可认为是刚性的,即变形可忽略不计,因此选择在铰链的端部及长臂处打圆孔,以此来减轻铰链的自身重量,以减小变形区域的变形量。

3.2 减小塑性变形

为了进一步避免铰链的长期形变,在铰链的中心处增加一个销柱,在测力时,销柱不会造成影响。测力完成后将销钉从铰链端部的销孔中插入到销柱中心的销孔中,这样铰链端部就不会长期处于悬垂状态,可减小因长期悬置造成的塑性变形。其结构如图6所示。

图6 减重和增加销钉后的铰链示意图

3.3 过重保护

对于铰链而言,其工作过程中最大应力应始终不得超过铝合金材料的许用应力,选择安全系数2,得到其许用应力[σ]=σs/nst=140 MPa。

使用workbench软件对铰链进行应力、变形分析,对铰链端部的四个圆孔施加固定约束,添加重力加速度载荷,并在铰链端部施加向下的力F,改变F大小,同时观察铰链的最大应力σmax以及铰链变形量。当最大应力为约140 MPa时,图7中A点处的铰链位移值约为5.1 mm。

图7 过重保护示意图

由于平行四边形铰链的总宽度为20 mm,两个臂分别宽2 mm,将中间的销柱宽度h设计为5.8 mm,这样铰链在变形中达到许用应力时刚好触碰到销柱上。

对没有销柱结构的铰链和有销柱的铰链分别施加重力载荷和力F进行有限元仿真分析,对比铰链的最大应力,应力值如表1所示。

表1 两种铰链施加载荷后的应力值对比

从表1中数值可以看出,销柱的存在可有效降低超负荷作用下的铰链最大应力,起到了很好的过重保护作用。

4 模态分析

在本系统中,平行四边形铰链一端连接于固定支承,另一端支撑内电极使其悬置于外电极中。这种结构使柔性铰链易受外界振动的影响而发生自振。因此,采用有限元分析软件对柔性铰链进行模态分析,找到其谐振频率,并选用相应的低通隔振台,以避免铰链与周围环境发生共振。

模态分析时,将铰链和内电极的组合模型导入到workbench有限元分析软件中,设置铰链和内电极材料为铝合金,然后对模型进行网格划分,在柔性铰链端部的四个圆柱孔内表面施加固定约束,最后进行模态分析,分析结果为前六阶固有频率值如表2所示。

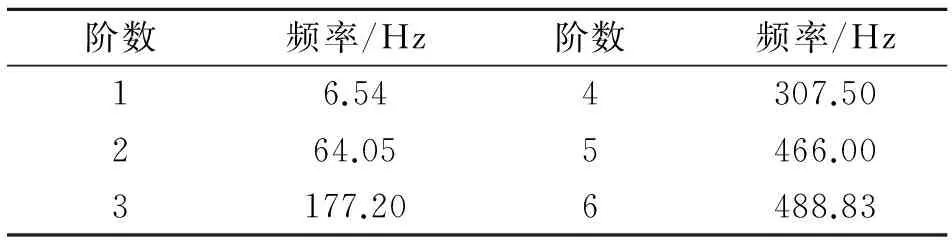
表2 前六阶固有频率值

这里选择低通截止频率为2 Hz的隔振台,滤掉环境中存在的各种高频振动,以避免与铰链系统发生共振。

5 实验

5.1 刚度标定

搭建图8所示的微纳力值测量系统,分别将2 mg、5 mg和10 mg的标准质量块加载到质量托盘,并用激光干涉仪以20 Hz的频率记录铰链端部位移,以此测试平行四边形铰链刚度,测试结果如图9所示。

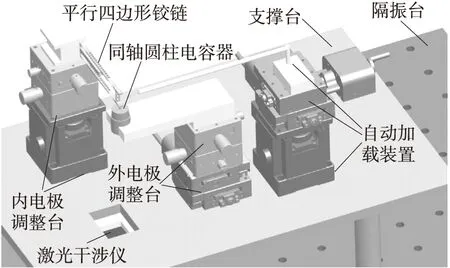
图8 实验装置

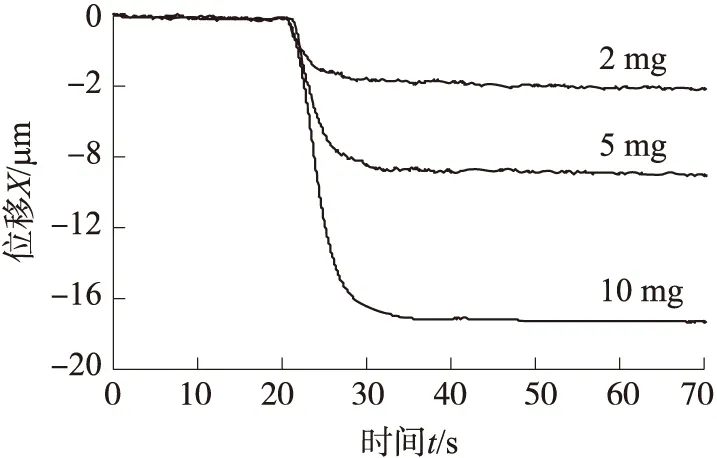
图9 加载标准质量块后的位移曲线

显然,铰链端部位移有一定程度的漂移,根据公式k=mg/x可求得三次加载的刚度值,其中天津地区的重力加速度g为9.801 1 N/kg,刚度测试结果为5.487 9 N/m,与设计值5 N/m相比稍大一些,其原因主要是铰链最薄处厚度t加工的误差,其影响在2.2.3节已经叙述。

5.2 平行四边形柔性铰链用于力值测量实验

将图8所示装置放入密闭玻璃罩进行力值测量实验,为了减小铰链漂移对力值测量的影响,借鉴砝码检定时使用的ABA单次循环法[15],即将微小质量环通过加载—卸载—加载的方式循环施加到质量托盘,记录每个加载后电压Um以及相邻两个空载电压值U01和U02,通过式(10)计算得相应力值:

(10)

其中电容梯度值dC/dz通过实验标定为0.86 pF/mm。

具体的实验过程如下:

①在内外电极之间施加180 V的初始偏置电压,将装置静置一段时间后,铰链运动到平衡位置,铰链自身的弹性力与此时刻的电压产生的静电力相互平衡。②开始执行测量系统的PID控制功能对内外电极之间的电压值进行控制以对铰链位移进行反馈调节。③此后通过自动加载装置将微小质量环通过加载—卸载—加载的方式循环施加到质量托盘。在此过程中控制电源的电压值可被自动保存。④对电压值进行适当滤波,根据式(10)计算力值大小。

目前国内可校准的最小标准质量在mg级别,其可产生的重力值在10-5N量级,无法用来测试基于平行四边形柔性铰链的微力测量系统对于μN量级的力值测量性能,且片状质量块难以实现循环加载,因此实验室自制了用来产生微小力的质量环,如图10所示,其材料选择了质量稳定、抗氧化性能强的金箔,尺寸足够小的金箔质量环即可产生μN量级的力,用以测试测量系统在μN量级范围工作的性能。

图10 金箔质量环

在一次测量中,设定加载时间80 s,卸载时间80 s,记录的电压值如图11所示。

图11 单次测量中记录的电压值

根据式(10)可计算得到力值平均值为3.511 7 μN,由于铰链自身存在一定的位移漂移,该漂移最终反映到了控制电压上,应用ABA单次循环法可有效减小漂移造成的误差。

在一周内对该质量环在相同的测量环境中进行反复测量,并计算电压对应的重力值,得到结果如图12所示。

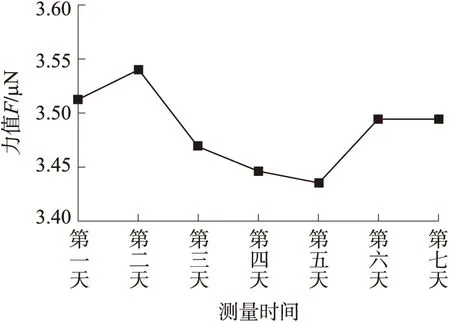
图12 力值多次测量结果

其均值为3.483 6 μN,方差为0.037 0 μN,相对标准偏差为1.061 6%,实验结果表明,该平行四边形柔性铰链可应用于10-6N量级的力值测量系统,且测量重复性较好。

测量误差的主要来源:环境振动以及质量环加载与卸载时产生的扰动;平行四边形柔性铰链由于内应力等因素而产生的位移漂移;电容梯度的测量误差;电源输出电压的误差;实验室温度和湿度变化造成的激光干涉仪的输出误差等。

6 结论

设计了一种用于μN量级力值测量的平行四边形柔性铰链机构。探讨了平行四边形柔性铰链的运动特点,抽象其数学模型,推导出了平行四边形铰链的静态和动态刚度公式,分析了薄臂处加工精度对于刚度的影响。借助有限元分析软件对铰链结构进行了优化设计,并分析得到其固有频率。最终将设计出的柔性铰链用于微力测量系统,得到其刚度值,并在相同条件下对质量环重力反复测量,结果表明该平行四边形柔性铰链可应用于10-6N～10-5N的微力测量系统,且具有较好的重复测量精度。

[1] Pratt J R,Kramar J A,Newell D B,et al. Review of SI Traceable Force Metrology for Instrumented Indentation and Atomic Force Microscopy[J]. Measurement Science and Technology,2005,16(11):2129.

[2]张军,李寒光,李映君,等. 压电式轴上六维力传感器的研制[J]. 仪器仪表学报,2010,3(1):73-77.

[3]Pratt J R,Kramar J A. SI Realization of Small Forces Using an Electrostatic Force Balance[C]//CD Proc XVIII IMEKO World Congress on Metrology for a Sustainable Development,Rio de Janeiro,Brazil,September. 2006:17-22.

[4]Pratt J R,Newell D B,Kramar J A,et al. Realizing and Disseminating the SI Micronewton with the Next Generation NIST Electrostatic Force Balance[C]//Proc ASPE 2004 Annual Meeting(Orlando,FL). 2004.

[5]Kim M S,Pratt J R,Brand U,et al. Report on the First International Comparison of Small Force Facilities:A Pilot Study at the Micronewton Level[J]. Metrologia,2012,49(1):70.

[6]Chen Shengjui,Pan Sheaushi. A Force Measurement System Based on Anelectrostatic Sensing and Actuating Technique for Calibrating Force in Amicro-Newton Range with a Resolution of Nanonewton Scale[J]. Measurament Science and Technology,2011(22):1001-1008.

[7]Chen S J,Pan S S. Nanonewton Force Generation and Detection Based on a Sensitive Torsion Pendulum IEEE Trans Instrum[J]. Meas,2009,5:8 897-901.

[8]盛阳,赵美蓉,刘明,等. 超微力发生系统及其电容采集模块的设计[J]. 传感技术学报,2010,23(10):1505-1509.

[9]刘明,林玉池,郑叶龙,等. 利用静电场原理复现微小力值的实验研究[J]. 传感技术学报,2012,25(1):33-36.

[10]左行勇,刘晓明. 三种形状柔性铰链转动刚度的计算与分析[J]. 仪器仪表学报,2007,27(12):1725-1728.

[11]陈贵敏,刘小院,贾建援. 椭圆柔性铰链的柔度计算[J]. 机械工程学报,2006,42(B05):111-115.

[12]张霖,王建华. 单平行四杆柔性铰链机构刚度特性分析[J]. 华东交通大学学报,2013(6):55-58.

[13]念龙生,隆志力,张璐凡,等. 基于刚度误差的直角柔性铰链设计可行域分析[J]. 纳米技术与精密工程,2014,12(1):15-21.

[14]Chen H. Analysis of the Rigidity of Arc Flexible Hinge with Different Geometrical Parameters[M]//Computer and Computing Technologies in Agriculture V. Springer Berlin Heidelberg,2012:195-200.

[15]李力,刘丽军. F_2等级砝码折算质量测量不确定度分析[J]. 中国计量,2012(2):81-82.

蔡雪(1990-),女,硕士研究生,天津大学精密仪器与光电子工程学院,主要从事微纳力值测量与溯源研究,caixue1102@163.com;

赵美蓉(1967-),女,教授及博士生导师,天津大学精密仪器与光电子工程学院,主要从事光电测控技术、视觉检测技术和微纳测控技术的研究,meirongzhao@tju.edu.cn。

DesignofFlexureHingeMechanismfor10-6N～10-5NMicroForceMeasurement*

CAIXue,ZHAOMeirong*,ZHENGYelong,ZHANGGuoqiang

(State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China)

In a micro-nano force measurement system based on the principle of static electric field,the mechanism used for force transmission and transformation plays a vital role. The parallelogram flexible hinge mechanism is used as elastic element,in order to realize the measurement of force on the scale of 10-6N. The mathematical model of the flexible hinge is analyzed to study the static and dynamic stiffness. The theory stiffness is determined according to the system requirement. The finite element method is used for the optimization design and modal analysis. The influence to the hinge stiffness of the machining accuracy is analyzed. The stiffness test and force value measurement results are given by experiments. Results show that the parallelogram flexible hinge can be used in the force measurement system on the scale of 10-6N.

micro force measurement;flexible hinge;finite element;stiffness

项目来源:国家科技支撑计划项目(2011BAK15B06)

2014-07-02修改日期:2014-09-19

10.3969/j.issn.1004-1699.2014.11.002

TH823;O441.1

:A

:1004-1699(2014)11-1451-06