Improved DV-Hop Location Algorithm Based on Hop Correction*

WEN Jiangtao，FAN Xuemin，WU Xijun

(Key Lab of Measurement Technology and Instrumentation of Hebei Province，Yanshan University，Qinhuangdao，Hebei066004，China)

Improved DV-Hop Location Algorithm Based on Hop Correction*

WEN Jiangtao*，FAN Xuemin，WU Xijun

(Key Lab of Measurement Technology and Instrumentation of Hebei Province，Yanshan University，Qinhuangdao，Hebei066004，China)

To solve the problem that the hop value in traditional DV－Hop algorithm can’t represent the real distance，an improved algorithm based on RSSI is proposed.First of all，the first hop is subdivided into several grades based on RSSI，then the rest hops are modified with the distance ratio of adjacent nodes which is transformed into the corresponding relationship of the RSSI.The simulation results show that the proposed algorithm in the paper possesses of the higher location precision than the traditional algorithm without extra hardware in the same network environment. Key words:wireless sensor network;DV－Hop;received signal strength indicator(RSSI);hop correction;localization accuracy

无线传感器网络的定位算法大致可分为两类:一类是基于测距(Range－Based)的定位算法，其中最常用的是基于接收信号强度指示(RSSI)［1］的测距方法。另一类是无需测距(Range－Free)的定位算法。非测距定位算法不需要测量相关物理量信息，而是通过节点之间的网络连通性来进行定位［2］，其凭借在功耗、成本等方面的优势，受到越来越多的关注。目前主要有质心算法(Centroid)［3］、DV－Hop［4－5］算法、APIT算法［6］和Amorphous［7］等算法。其中DV－Hop算法巧妙地将节点间的距离测量转化为跳数与平均跳距的乘积，是目前研究最广泛的算法之一。

针对DV－Hop算法在拓扑不规则的网络中定位误差较大的问题的研究已经取得了一些成果。文献［8］采用最小均方误差准则对平均每跳距离进行修正，文献［9］首先采用最小二乘法对信标节点间的平均跳距修正，然后对未知节点收到的平均跳距进行加权处理，这两种改进算法主要修正的是平均跳距，定位精度提高的同时计算量也显著增大。文献［10］只对信标节点与未知节点之间的跳数作了修正，并未考虑未知节点之间跳数的优化。文献［11］利用相邻节点接收到的RSSI的比值对跳数进行加权，其直接把RSSI的比值作为权值修正跳数，精度提高不明显;针对上述算法的不足本文作了如下改进:引入RSSI测距技术对第1阶段的最小跳数值从两个方面进行了修正，首先基于信标节点的直接邻居节点接收到的RSSI对第1跳分级，细化跳数，然后把跳数间实际距离的比值作为权值，并将其转化为RSSI的关系式对跳数进行加权处理使其更接近实际值，进而提高定位精度，通过仿真比较了改进算法与原始算法的性能。

1 DV－Hop算法原理

DV－Hop算法是一种基于距离矢量的分布式定位算法［12］。其定位过程大致分为3个阶段。

第1阶段:通过典型的距离矢量交换协议，使网络中所有节点得到距离每个信标节点的最小跳数值。

第2阶段:每个信标节点在获得其他信标节点的位置信息和最小跳数后，根据式(1)计算自身的平均每跳距离:

其中，(xi，yi)，(xj，yj)分别为信标节点i，j的坐标，hij(i≠j)表示信标节点i，j之间的最小跳数。该信标节点将计算得到的平均跳距利用可泛洪方式广播到网络中。未知节点仅记录收到的第1个跳距值并将该值转发，然后结合第1阶段得到的最小跳数值求得与相应信标节点的距离。

第3阶段:未知节点得到3个或3个以上与信标节点的距离后，利用三边定位法或极大似然估计法计算自身的位置坐标，从而完成定位。

2 DV-Hop算法改进

传统DV－Hop算法中，不直接测量邻居节点之间的物理量，如距离或角度，而是依据节点间的跳数信息与平均跳距的乘积来估计距离。

在第1阶段计算最小跳数的时候，只要通信半径R之内的距离无论远近都记为1跳，如图1所示，节点1，2的跳数都记为1，可是他们与信标节点D的实际距离相差很大，依赖这种不能反映实际距离大小的跳数值来定位，在节点均匀分布时尚且可以得到合理的平均跳距，但是网络拓扑一般是不规则的，运用相同的平均跳距来估计距离必然会产生较大的定位误差。

图1 跳数示意图

针对上述问题，本文引入距离这个因素来修正第1阶段的跳数以提高定位精度。以信标节点到直接邻居节点的距离作为基准，设其距离为L1，跳数为h1，以其他邻居节点间的距离与基准距离的比值作为权值修正该跳跳数。如图2所示，第2跳的权值为L2/L1，该跳跳数为h1·(L2/L1)。则节点3到信标节点E的跳数为h1·(1+L2/L1+L3/L1)。因为整个拓扑网络中第1跳的距离也差异很大，所以第1跳的跳数不能笼统的记为1，本文中对第1跳根据距离大小进行分级处理。

实际定位过程中距离是未知的，但是大多数节点都有检测信号强度(RSSI)的能力，而RSSI是一种利用信号传播过程中不断衰减的信号强度来推测距离的测距技术。所以在传统DV－Hop算法中引入RSSI测距技术进行辅助定位以降低定位误差。

2.1 RSSI测距原理

无线传感器网络中应用最广泛的信号传播损耗模型是Shadowing模型［13］，其表达式如下:

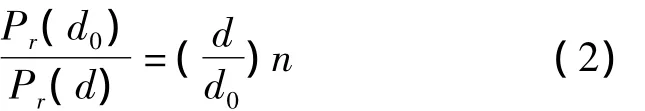
上式中:d为接收端与发射端的距离，d0为选定的一个与发射端的参考距离，通常选为1 m。Pr(d)表示距离为d时的平均接收功率，单位为W。n为实际测量环境的路径损耗因子，范围在2～6之间。

在上述模型中引入了一个均值为零，标准差为σ服从高斯分布的随机噪声，用Xσ表示。若功率以dB作为计量单位，设距离发射节点为d时的接收功率为Pr(d)dB，且令d0=1 m，并设A为距离发射端1 m处多次测量所得RSSI值的平均值，则根据式(2)可以推导出距离发射端为d处的RSSI值为

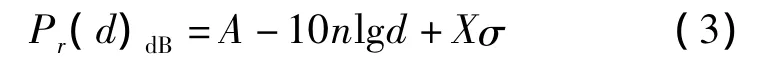
Shadowing 模型描述了节点接收功率与信号传播距离的关系，一般情况下距离发射端越远的节点接收到的RSSI值越小。未知节点可以根据自己接收到的RSSI值通过Shadowing模型直接计算与信标节点的距离。下面利用RSSI值与距离的关系对DV－Hop算法中的跳数值进行修正。

2.2 跳数修正

2.2.1 基于RSSI对第1跳分级

本文是以第1跳的距离作为基准作加权处理的，所以第1跳的跳数值h1需反映出距离的大小。鉴于通信半径R对同一批节点而言是相对固定的，因此把R设为1跳的理想距离，然后对R做分级处理，每一级对应一个跳数，这样可以细化节点间的跳数，有助于提高测距精度进而提高定位精度。

设节点的通信半径为R，把第1跳分为m级，信标节点与其直接邻居节点间的实际距离为x，第1跳的跳数记为h1，i为小于m的正整数，则

实际定位过程中距离是未知的，但是每个节点都有接收RSSI的能力，所以可以根据信号传播衰减模型的式(3)把跳数与距离的关系转化为跳数与接收功率的关系。当时，相应的RSSI值的关系为

由于跳数对应一个功率值的区间，而高斯噪声引起功率值的波动远远小于这个区间，所以噪声对跳数值影响不大可以忽略，则第1跳的跳数与对应接收功率的关系如下所示上式根据信标节点的直接邻居节点接收到的RSSI值对跳数进行分级细化，该方法使DV－Hop算法中的跳数值不再是整数，而是小数，这有效地提高了跳数值的准确性，从而降低了定位误差。也为后续跳数的加权修正计算提供了保证。

2.2.2 利用RSSI对跳数加权修正

引入权值的定义:在大于一跳的跳数中，权值Hj设为第j跳与第1跳实际距离的比值，其中j为正整数

同理，需要把权值与距离的关系转化为权值与接收功率的关系。Shadowing模型的表达式(2)描述了接收功率与信号传播距离的关系，该公式里接收功率的单位是W(瓦特)，但是在实际的无线信号传播过程中，功率常是以dB作为计量单位，以RSSI值的形式从寄存器或是从数据包中获取的。所以对式(2)进一步转化，设距发送端为d处的节点接收到的RSSI用Pr(d)dB表示，则式(2)可写为

根据式(7)把权值转化为节点接收到的RSSI值的关系式

得到权值后与第1跳跳数h1相乘便为该跳的修正跳数，这种方法可以修正所有节点间的跳数，也包括信标节点间的跳数，进而可以修正平均每跳距离，使测距误差进一步降低。

2.3 改进后算法的具体步骤

对跳数进行分级和加权处理后改进算法的具体步骤如下:

(1)第1跳:在信标节点广播的信息数据包中加入一个新的数据量，RSSI值，即信息数据包为{ID，(x，y)，Hopcount，RSSI}，其中ID为信标节点编号，(x，y)为信标节点位置坐标，Hopcount为当前数据包的跳数，初始值为0。其直接邻居节点收到该数据包后根据式(5)计算第1跳的跳数，更新Hopcount域，并记录收到该数据包时的RSSI值。

(2)其余跳:网络中其他节点收到直接邻居节点转发的数据包后用自身接收该数据包时的RSSI值与数据包中的RSSI值利用式(8)获得该跳的权值Hj，并将数据包中的跳数加上加权跳数后保存下来，即Hopcountj=Hopcountj－1+Hjh1，同时将更新后的数据包转发给它的邻居节点，但RSSI域并不更新，其一直保存的是第1跳接收到的RSSI值。

(3)第2阶段与第3阶段仍按照标准的DVHop算法计算平均跳距并利用最小二乘法计算未知节点的坐标，完成定位。

3 仿真结果验证

为了比较改进后的DV－Hop算法与传统DVHop算法的性能，在MATLAB 7.0平台上进行了仿真实验，并和文献［11］中基于相邻节点间RSSI直接相除进行加权的改进算法进行了比较，下面分别研究了在不同锚节点比例，通信半径下传统算法与改进算法的定位精度。

3.1 仿真环境及参数设定

仿真环境是在100 m×100 m的正方形区域内随机分布100个节点，从中随机选取信标节点，设所有节点具有相同的通信半径R。为了消除由于节点随机分布造成的误差的不稳定性，在相同的网络环境下分别进行1 000次仿真实验取平均值。

归一化定位误差是衡量算法定位精度的指标［14］。设节点i的真实位置为Xi，估计位置为X'i，则定位误差为|Xi－X'i|，共有N个未知节点，节点通信半径为R，共仿真K次，则所有未知节点的平均定位误差error为

则归一化定位误差为:

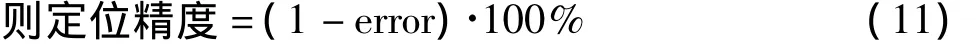
3.2 算法精度分析

图3是通信半径R=30 m，第1跳分为不同级数时，节点的定位误差图。从图中可以看出随着信标节点比例的增大，3条曲线的定位误差都在降低。而且所分级数越多，定位误差越小，这是因为m=3比m= 2时所得跳数值更准确所以定位精度更高。但是m =2比m=1的精度提高了6%左右，而m=3比m= 2只提高了4%左右，可见随着级数的增大，误差降低的百分比会越来越小。而且分级越多计算量便越大，折中选择，本文算法中所选的级数为m=3。

图3 不同级数时的归一化误差

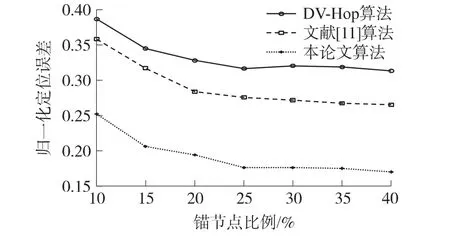
图4归一化定位误差与锚节点比例的关系

图4 给出了通信半径为30 m时未知节点归一化定位误差与信标节点比例的关系曲线，由仿真结果可以看出，算法误差随着信标节点比例的增加而减小并趋于稳定。在同一锚节点比例时，本论文提出改进算法的定位精度比传统DV－Hop算法提高了15%左右，而文献［11］提出的改进算法定位精度只能提高5%左右，由此可见，本文提出的算法改进更有效。

图5给出了信标节点比例为30%时，归一化定位误差与通信半径R的关系，从图中可以看出随着通信半径的增大，节点定位误差都有减小的趋势，但是本文算法受通信半径的影响最小，这是因为本文的改进算法有效地修正了节点间的跳数，使半径增大时跳数误差没有明显增大，而且在同一半径下本文提出算法的定位精度最高。

图5 归一化定位误差与通信半径的关系

3.3 算法复杂度分析

表1给出了本文算法与其他算法在通信开销，算法复杂度，硬件复杂度上的性能比较。设网络中节点总数为N，信标节点数为A。表中的定位精度选取通信半径为30 m，锚节点比例为25%时的数据，按照式(11)计算得到。因为本文的改进算法只在数据包中添加了一个RSSI量，并未改变数据包的传送路径所以通信开销并未增加。从表1中可以看出与传统DV－Hop算法相比，本文改进算法在以不增加通信开销的基础上以较小的计算量代价获得了更高的定位精度。

表1 各种算法性能比较

在处理器主频为3.30 GHz内存为2.0 Gbyte的计算机上，对传统DV－Hop算法仿真运行1 000次的时间为3.309 s，本文所提出的改进算法为4.958 s，可见单次时间差为1.6 ms左右，这是由于本文算法在计算跳数时引入RSSI值对跳数进行修正使得计算量有所增加，但依然具有较快的速度满足实时定位的要求。

4 结论

本文提出的基于RSSI的DV－Hop改进算法引入RSSI测距技术对原始DV－Hop算法中的跳数值从两个方面分别进行了修正，有效地解决了拓扑不规则网络中，因为跳数值不能反映实际距离大小而导致定位误差较大的问题，在无需增加额外硬件的条件下提高了定位精度。仿真结果表明在100 m×100 m的正方形区域，节点随机分布的网络环境下，改进后算法的定位精度比原始算法提高了15%左右。

［1］Deng－Yin Z，Guo－Dong C.A Union Node Localization Algorithm Based on RSSI and DV－Hop for WSNs［C］//Instrumentation，Measurement，Computer，Communication and Control(IMCCC)，2012 Second International Conference on.IEEE，2012:1094－1098.

［2］Zheng J，Wu C，Chu H，et al.An Improved DV－Hop Localization Algorithm［C］//Progress in Informatics and Computing(PIC)，2010 IEEE International Conference on IEEE，2010，1:469－471.

［3］Hongyang C，Sezaki K，Ping D，etal.An Improved DV－Hop Localization Algorithm with Reduced Node Location Error for Wireless Sensor Networks［J］.IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2008，91(8): 2232－2236.

［4］Chen H，Sezaki K，Deng P，et al.An Improved DV－Hop Localization Algorithm forWireless Sensor Networks［C］//Industrial Electronics and Applications，2008.ICIEA 2008.3rd IEEE Conference on.IEEE，2008:1557－1561.

［5］Zhang J，Wu Y H，Shi F，et al.Localization Algorithm Based on DV－HOP for Wireless Sensor Networks［J］.Journal of Computer Applications，2010，30(2):323－326.

［6］Tian S，Zhang X，Liu P，etal.A RSSI－Based DV－Hop Algorithm for Wireless Sensor Networks［C］//Wireless Communications，Networking and Mobile Computing，2007.WiCom 2007.International Conference on IEEE，2007:2555－2558.

［7］Zhou Z，Xiao M，Liu L，et al.An Improved DV－HOP Localization Algorithm［C］//Information Science and Engineering(ISISE)，2009 Second International Symposium on IEEE，2009:598－602.

［8］嵇玮玮，刘中.DV－Hop定位算法在随机传感器网络中的应用研究［J］.电子与信息学报，2008，30(4):970－974.

［9］林金朝，陈晓冰，刘海波.基于平均跳距修正的无线传感器网络节点迭代定位算法［J］.通信学报，2009(10):107－113.

［10］Guo Z，Min L，Li H，et al.Improved DV－Hop Localization Algorithm Based on RSSIValue and Hop Correction［M］.Advances in Wireless Sensor Networks.Springer Berlin Heidelberg，2013:97－102.

［11］周小波，乔钢柱，曾建潮.无线传感器网络中基于RSSI的加权DV－HOP定位方法［J］.计算机工程与应用，2011，47(14): 109－111.

［12］肖丽萍，刘晓红.一种基于跳数修正的DV－Hop定位算法［J］.传感技术学报，2012，25(12):1726－1730.

［13］赵昭，陈小惠.无线传感器网络中基于RSSI的改进定位算法［J］.传感技术学报，2009，22(3):391－394.

［14］张爱清，叶新荣，胡海峰，等.基于RSSI每跳分级和跳距修正的DV－HOP改进算法［J］.仪器仪表学报，2012，33(11):2552－2559.

温江涛(1974－)，男，博士，燕山大学电气工程学院讲师，硕士生导师，主要从事基于无线传感网络的定位、识别等研究，wens2002@163.com;

范学敏(1987－)，女，燕山大学电气工程学院硕士研究生，主要从事无线传感器网络定位的研究，bingchenmin@ 163.com;

吴希军(1979－)，男，博士，燕山大学电气工程学院副教授，主要从事传感系统构建与光谱测试方面的研，wuxijun@ysu.edu.cn。

基于RSSI跳数修正的DV－Hop改进算法*

温江涛*，范学敏，吴希军

(河北省测试计量技术及仪器重点实验室，燕山大学，河北秦皇岛066004)

针对原始DV－Hop算法中跳数值不能反应出节点间实际距离大小而导致拓扑不规则网络中节点定位误差较大的问题，提出了一种基于接收信号强度指示RSSI(Rceived Sgnal Srength Idicator)的改进算法。首先根据直接邻居节点接收到的RSSI值对第1跳进行分级，细化跳数;同时把节点间的距离比值作为权值，并将其转化为相应RSSI的关系对跳数进行加权修正，使获得的跳数值更准确。仿真结果表明在相同的网络环境下，与传统算法相比改进算法在不增加额外硬件的前提下有效地提高了定位精度。

无线传感器网络;DV－Hop;接收信号强度指示(RSSI);跳数修正;定位精度

TP393

A

1004－1699(2014)01－0113－05

2013－07－08修改日期:2013－12－30

C:6150P

10.3969/j.issn.1004－1699.2014.01.021

项目来源:国家自然科学基金项目(51204145);河北省自然科学基金项目(2013203300)